Учебная работа. Курсовая работа: Исследование индуцированной шумом синхронизации в системах с дискретным временем
Федеральное агентство по образованию
ГОУ ВПО «САРАТОВСКИЙ государственный УНИВЕРСИТЕТ ИМЕНИ Н.Г.ЧЕРНЫШЕВСКОГО»
Кафедра нелинейной физики
КУРСОВАЯ РАБОТА
исследование индуцированной шумом синхронизации в системах с дискретным временем
студента 3 курса факультета нелинейных процессов
Костакова Алексея Александровича
Научный руководитель
ассистент ______________________ О.И. Москаленко
Зав. кафедрой,
профессор, д.ф.-м.н. ______________________ Ю.П. Шараевский
Саратов – 2008
Содержание
Введение
синхронизация колебаний
Цель работы
Синхронизация, индуцированная шумом
Численное моделирование
Вывод
список литературы
Введение
Одна из главных тенденции в мире ‑ тенденция к достижению общих ритмов взаимного поведения или, другими словами, тенденция к синхронизации. Под синхронизацией обычно понимается процесс достижения связанными объектами различной природы общего ритма функционирования.
С проявлением синхронизации можно встретиться в физике, биологии, химии, технике, экономике, науках о жизни, медицине и т.д. Возможна синхронизация как двух элементов, так и в ансамблях, состоящих из сотен и тысяч элементов. В радиофизике интенсивно исследуется коллективное синхронизация используется для синтеза и стабилизации частоты генераторов, для демодуляции сигналов в доплеровских системах, в системах точного времени и т.д. В механике эффект синхронизации нашел широкое применение при конструировании различных вибро-технических устройств. В качестве примеров биологических ансамблей, в которых наблюдается синхронизация, приведем: колонии одновременно вспыхивающих светлячков; клетки, формирующие сердечный ритм; вырабатывающие инсулин клетки в поджелудочной железе; группы сверчков, щебечущих в унисон; ячейки в тонкой кишке млекопитающих; нейронные ансамбли, обеспечивающие ритмичную деятельность в мозгу и т.д. Проблемы синхронизации также очень важны при проектировании компьютеров с параллельной архитектурой. Синхронизации имеет место в химических колебаниях и волнах в реакции Белоусова-Жаботинского.
В связи с чрезвычайно широким распространением синхронизации в природе, науке и технике Потребность изучения этого явления и его применений обусловила появление специального раздела в теории нелинейных колебаний и волн ‑ теории синхронизации.
синхронизация колебаний
Синхронизация колебаний – одно из важнейших нелинейных явлений, привлекающих к себе широкое внимание исследователей, имеющих как теоретическое, так и практическое скрытой передаче информации с помощью хаотических сигналов, при управлении системами сверхвысокочастотной электроники и т.п.).
С развитием теории динамического хаоса было выявлено достаточно различных типов хаотического синхронного поведения связанных динамических систем:
— фазовая синхронизация
— обобщенная синхронизация
— лаг-синхронизация
— перемежающаяся фазовая синхронизация
— перемежающиеся лаг-синхронизация
— перемежающаяся обобщенная синхронизация
— полная синхронизация
Каждый из этих типов синхронной хаотической динамики имеет свои особенности и способы диагностики, при этом в научной литературе активно обсуждается вопрос о взаимосвязи этих типов синхронного поведения. разные типы синхронизации связанных хаотических осцилляторов могут рассматриваться как различные виды проявления единых закономерностей, возникающих в связанных нелинейных системах.
Цель работы
Целью работы является изучение индуцированной шумом синхронизации: определение и методы ее диагностики. А также построить программу, с помощью которой можно наблюдать явление индуцированной шумом синхронизации, для двух отображений:
1.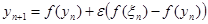 [1]
[1]
, где 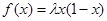
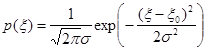
2. 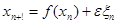 [2]
[2]
, где 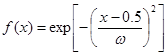
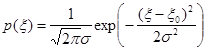
А также построить для этих отображений зависимость ляпуновской экспоненты 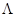 от параметра связи
от параметра связи  ; и сравнить пороговое значение
; и сравнить пороговое значение  (т.е. при котором
(т.е. при котором 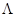 становится отрицательным) с результатами, полученными с помощью программы. А также сравнить полученные мной данные с результатами приведенными в [1] и [2].
становится отрицательным) с результатами, полученными с помощью программы. А также сравнить полученные мной данные с результатами приведенными в [1] и [2].
синхронизация, индуцированная шумом
Под режимом синхронизации, индуцированной шумом, понимается следующее: случайный сигнал 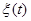 , действующий на две независимые, но идентичные хаотические системы
, действующий на две независимые, но идентичные хаотические системы 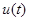 и
и 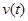 (с разными начальными условиями
(с разными начальными условиями 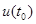 и
и 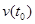 , лежащими в бассейне притяжения одного и того же хаотического аттрактора), может приводить к тому, что эти системы “синхронизуются” друг с другом, то есть после завершения переходного процесса они начинают демонстрировать идентичное поведение
, лежащими в бассейне притяжения одного и того же хаотического аттрактора), может приводить к тому, что эти системы “синхронизуются” друг с другом, то есть после завершения переходного процесса они начинают демонстрировать идентичное поведение 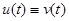 .
.
Но установление синхронной динамики двух систем с общим источником шума возможно лишь в том случае, когда все условные ляпуновские экспоненты оказываются отрицательными.
далеко не всегда удается наблюдать синхронизацию, индуцированную шумом, в хаотических осцилляторах, поскольку хаотические системы должны обладать определенными свойствами (сильное сжатие фазового объема в фазовом пространстве, ограниченная область фазового пространства, где наблюдается увеличение фазового объема и др.)
Механизмы возникновения
Возможны два похожих механизма, приводящих к возникновению режима индуцированной шумом синхронизации:
1. Случайный сигнал 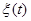 имеет ненулевое среднее, что фактически переводит систему в нехаотический режим, при котором состояние системы просто ‘следует’ за внешним случайным возмущением
имеет ненулевое среднее, что фактически переводит систему в нехаотический режим, при котором состояние системы просто ‘следует’ за внешним случайным возмущением 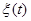 .
.
2. внешний сигнал большой интенсивности (может быть, даже с нулевым средним значением) переводит изображающую точку в области фазового пространства с большим сжатием фазового потока, которая находится в этих областях большую долю времени, в результате чего в среднем имеет место сходимость соседних траекторий.
В обоих случаях определяющую роль играет сжатие фазового потока, при этом условные ляпуновские экспоненты имеют отрицательные значения.
Связь обобщенной синхронизации и синхронизации,
индуцированной шумом
Режим обобщенной синхронизации означает, что между состояниями взаимодействующих однонапрвленно связанных ведущего 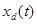 и ведомого
и ведомого 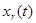 хаотических осцилляторов (с непрерывным или дискретным временем), существует такая функциональная зависимость
хаотических осцилляторов (с непрерывным или дискретным временем), существует такая функциональная зависимость 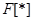 , что после завершения переходного процесса устанавливается функциональное соотношение
, что после завершения переходного процесса устанавливается функциональное соотношение 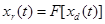 .
.
Сам вид данной зависимости 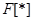 (гладкая или фрактальная) может быть достаточно сложным, а процедура ее нахождения весьма нетривиальна. Выделяют сильную и слабую обобщенную синхронизацию. Следует отметить, что в качестве взаимодействующих осцилляторов могут выступать две разные динамические системы, в том числе и с различной размерностью фазового пространства.
(гладкая или фрактальная) может быть достаточно сложным, а процедура ее нахождения весьма нетривиальна. Выделяют сильную и слабую обобщенную синхронизацию. Следует отметить, что в качестве взаимодействующих осцилляторов могут выступать две разные динамические системы, в том числе и с различной размерностью фазового пространства.
Очевидно, что режим обобщенной хаотической синхронизации и режим синхронизации, индуцированной шумом, несмотря на то, что традиционно считаются разными явлениями, на самом деле обусловлены проявлениями одного и того же механизма и вызваны одной и той же причиной – подавлением собственных хаотических колебаний с помощью дополнительного введения диссипации (либо с помощью ненулевого среднего значения шума в случае индуцированной шумом синхронизации, либо с помощью дополнительного диссипативного слагаемого в случае режима обобщенной синхронизации, либо смещением изображающей точки системы в области фазового пространства с сильной диссипацией).
Численное моделирование
Описание рассмотренных систем
1. Логистическое отображение под воздействием шума:
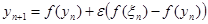 [3]
[3]
, где 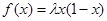 (1)
(1)
Значение управляющего параметра  ,
,  — параметр связи.
— параметр связи.
Случайная величина 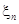 подчиняется нормальному распределению
подчиняется нормальному распределению 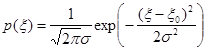 , где
, где 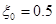 ,
, 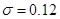 .
.
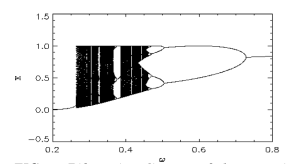
Бифуркационная диаграмма для данного отображения имеет вид:
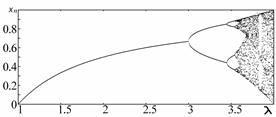
2. Одномерное отображение вида:
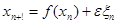 [4]
[4]
, где 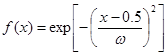 (2)
(2)
,  — параметр связи
— параметр связи
Случайная величина 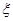 подчиняется нормальному распределению
подчиняется нормальному распределению  , где,
, где,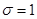 .
.
Бифуркационная диаграмма для данного отображения имеет вид:
Результаты, полученные с помощью созданной программы
1. Для отображения 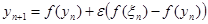 , где
, где 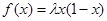 при
при 
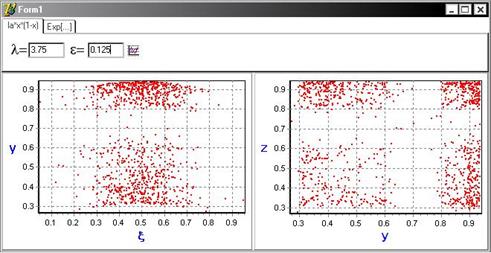
Видно, что в случае малого параметра связи (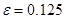 ) обе системы в один момент дискретного времени принимают разные значения (точки, характеризующие состояние систем, распределены по плоскости (y,z)), а следовательно не существует функциональной зависимости между случайным процессом и состоянием динамической системы.
) обе системы в один момент дискретного времени принимают разные значения (точки, характеризующие состояние систем, распределены по плоскости (y,z)), а следовательно не существует функциональной зависимости между случайным процессом и состоянием динамической системы.
С увеличением параметра связи 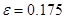 : точки соответствующие состояниям систем, лежаться на диагональ y=z, что свидетельствует о наличии синхронного поведения в системе.
: точки соответствующие состояниям систем, лежаться на диагональ y=z, что свидетельствует о наличии синхронного поведения в системе.
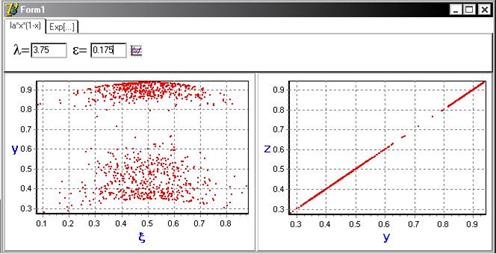
3. Для отображения 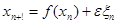 , где
, где 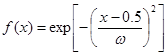 , при
, при 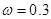 получаем аналогичные результаты: при
получаем аналогичные результаты: при 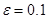 синхронизации не наблюдается:
синхронизации не наблюдается:
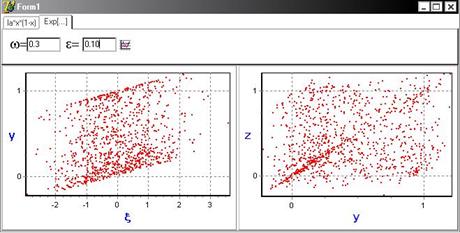
Но с увеличением параметра связи ε=0.2 появляется функциональная зависимость, что свидетельствует об установлении режима индуцированной шумом синхронизации.
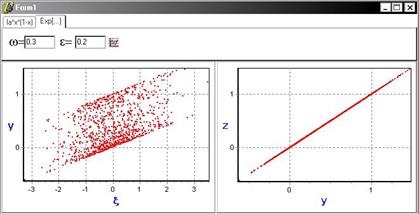
С помощью данной программы было найдено, что порог синхронизации индуцированной шумом:
-для первого отображения 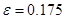
-для второго отображения 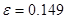
Ляпуновские экспоненты
Как уже было упомянуто ранее, установление синхронной динамики двух систем с общим источником шума возможно лишь в том случае, когда ляпуновские экспоненты оказываются отрицательными.
Для отображений ляпуновский показатель рассчитывается по формуле:
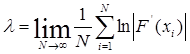 [5]
[5]
,
где F(x) – функция, задающая отображение.
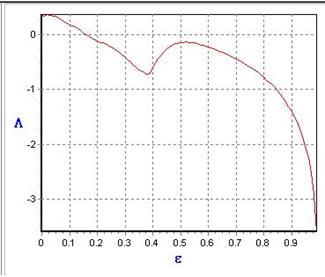
Для рассматриваемых систем зависимость ляпуновской экспоненты от управляющего параметра  имеет вид:
имеет вид:
1. 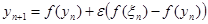 , где
, где 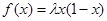
2. 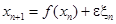 , где
, где 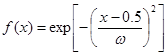

Видно, что для логистического отображения (1) ляпуновская экспонента становится отрицательной при e = 1.165, для отображения (2) – при e = 1.151.таким образом, результаты, полученные при помощи обоих методов диагностики, оказываются приблизительно одинаковыми.
Выводы
Было изучено явление индуцированной шумом синхронизации в системах с дискретным временем. Для диагностики синхронного режима производилось непосредственное сравнение векторов состояния идентичных систем, на которые воздействовал один и тот же источник шума, а также производился расчет условных ляпуновских экспонент. Рассмотрена взаимосвязь индуцированной шумом синхронизации с обобщенной синхронизацией. Была создана программа, иллюстрирующая явление индуцированной шумом синхронизации. С помощью этой программы рассмотрены два отображения. Также для этих отображений получены зависимости ляпуновской экспоненты от управляющего параметра. полученные результаты хорошо согласуются с результатами работ [1-3].
список литературы
1. А.А. Короновский, О.И. Москаленко, А.Е. Храмов “О механизмах, приводящих к установлению режима обощенной синхронизации”, ЖТФ, 76, 2 (2006) 1-9.
2. Raul Toral, Claudio R. Mirasso, E. Hernandez-Garcia and Oreste Piro “Analytical and Numerical Studies of Noise-induced Synchronization of Chaotic Systems”, CHAOS, 11, 3 (2001) 665-673.
3. A.E. Hramov, A.A. Koronovskii, O.I. Moskalenko “Are generalized synchronization a noise-induced synchronization identical types of synchronous behavior of chaotic oscillators”, Phys. Lett. A, 354, 5-6 (2006) 423-427.
4. С.П. Кузнецов Динамический хаос
5. Amos Martian, Jayanth R. Banavar “Chaos, Noise, and Synchronization”, Phys. Rev. letters, volume 72, number 10 (1994) 1451-1454
[1]
Отображение взято из работы
[1]
[2]
Отображение взято из работы
[2]
[3]
Отображение взято из работы
[1]
[4]
Отображение взято из работы
[2]
[5]
Взято из [4]

