Учебная работа. Лабораторная работа: Исследование динамических свойств моделей типовых звеньев систем автоматического управления
Лабораторная работа
«Исследование динамических свойств моделей типовых звеньев систем автоматического управления по их частотным характеристикам»
Введение
Цель работы – изучение экспериментального метода и аппаратных средств определения амплитудно-фазовых частотных и динамических характеристик типовых звеньев.
1. Теоретические сведения
Для сложного объекта автоматического регулирования не всегда удается произвести исследование с помощью аналитических методов ввиду того, чтозаранее неизвестны математические модели, параметры объекта или существуют значительные нелинейности в объекте. В этом случае применим экспериментальный метод построения частотных характеристик исследуемого объекта, базирующийся на том, что если на его вход подать сигнал синусоидальной формы с частотой и амплитудой, равной единице, то на выходе в установившемся режиме получится тоже синусоидальный сигнал с той же частотой но с другими амплитудой и фазой.
Синусоидальные функции могут выражаться в векторной форме показательными функциями с мнимым аргументом:
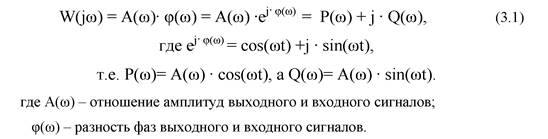
Величина W(j) называется комплексным коэффициентом передачи или усиления, представляющим комплексное число, модуль которого равен отношению амплитуд выходного и входного сигналов при неизменной частоте входного сигнала. Если положить =0, то получается коэффициент усиления или коэффициент передачи системы или звена.
Процесс регулирования Y(t) складывается из двух частей: переходного процесса YПП
(t) и установившегося процесса YУСТ
(t):
Y(t) = YПП
(t) +YУСТ
(t).
Математически переходный процесс определяется общим решением однородного уравнения (1.1), при Х(t)=0, а установившийся процесс – частным решением уравнения неоднородного уравнения (1.1), при заданной правой части Х(t). С точки зрения теоретической механики переходный процесс есть свободное движение системы, а установившийся процесс – вынужденное движение. С точки зрения теории колебаний первое есть собственные колебания, а второе – вынужденные колебания, но это ни в коем случае не означает, что переходный и установившийся процессы всегда по форме будут колебательными.Для получения переходной характеристики подают мгновенно скачком на вход звена некоторое постоянное значение вида:
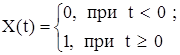
и наблюдают переходный процесс (свободные колебания) на выходе звена. На коммутационном поле АВМ эта модель входного воздействия реализуется на масштабном операционном усилителе с изменяемым согласно варианта задания коэффициентом усиления:
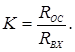
Такое идеальное звено не обладает инерционностью и мгновенно дает на выходе величину:
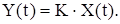 (1.2)
(1.2)
Если на вход звена или системы подать сигнал синусоидальной формы с частотой ω вида:
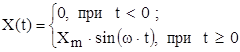 (1.3)
(1.3)
то на выходе в установившемся режиме получится тоже синусоидальный сигнал с той же частотой ω, но с другими амплитудой и фазой (наблюдение вынужденных колебаний звена).
2 Экспериментальная часть
Составим таблицу значений 2.1
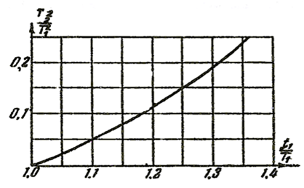
Построим график апериодического звена второго порядка, рисунок 2.1 и с помощью данного графика получим
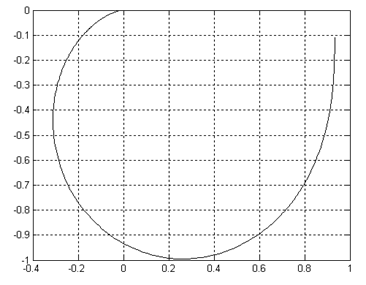
Рисунок 2.1 – график апериодического звена второго порядка Вычислив А(ω) и φ(ω), построим годограф, рисунок 2.2. Рисунок 2.2. – Годограф А(ω)φ(ω) Зная значение = 14 В, а = 15 В, можно рассчитать Исходя их графика для определения постоянных времени апериодического звена второго порядка, рисунок 2.3, найдём значение Рисунок 2.3 – График для определения постоянных времени апериодического звена второго порядка Следует можем найти Воспользовавшись программой MatLab, построим графики характеристик: ФЧХ, АЧХ, ВЧХ, МЧХ, КЧХ, ЛАЧХ и ЛФЧХ. В окна команд запишем: >> m=[0.93333] m = 0.9333 >> n=[1.3225 1.15 1] n = 1.3225 1.1500 1.0000 >> tf (m, n) Transfer function: 0.9333 1.323 s^2 + 1.15 s + 1 >> [h, w]=freqs (m, n, 600); >> ampl=abs(h); >> phi=angle(h); >> phi=unwrap(phi); >> plot (w, phi, ‘k’); grid on >> plot (w, ampl, ‘k’); grid on >> vchhar=ampl.*cos(phi); >> plot (w, vchhar, ‘k’); grid on >> mchhar=ampl.*sin(phi); >> plot (w, mchhar, ‘k’); grid on >> plot (vchhar, mchhar, ‘k’); grid on График ФЧХ представлен на рисунке 2.4. рисунок 2.4 – График фазочастотной характеристики График АЧХ представлен на рисунке 2.5. График ВЧХ представлен на рисунке 2.6. рисунок 2.6 – График вещественной частотной характеристики График МЧХ представлен на рисунке 2.7. График КЧХ представлен на рисунке 2.8. рисунок 2.8 – График комплексной частотной характеристики Для построения ЛАЧХ и ЛФЧХ составим структурную схему представленную на рисунке 2.9. рисунок 2.9 – Структурная схема для построения ЛАЧХ и ЛФЧХ
 .
.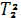 .
.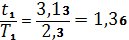
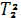 :
: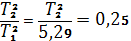
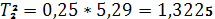
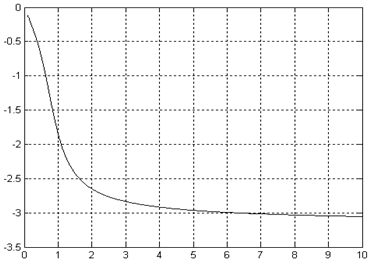
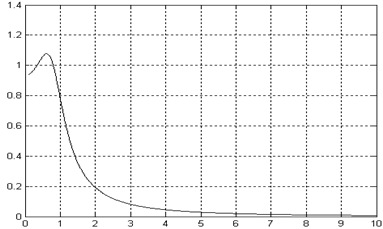
 рисунок 2.5 – График амплитудо-частотной характеристики
рисунок 2.5 – График амплитудо-частотной характеристики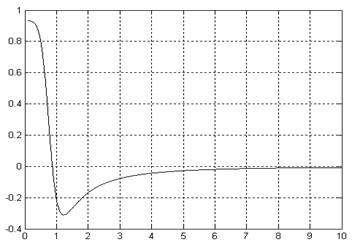
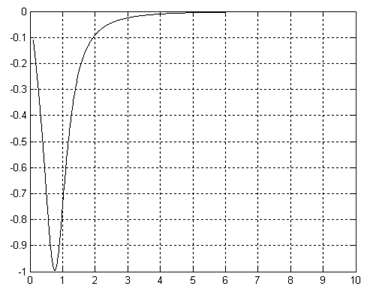
 рисунок 2.7 – График мнимой частотной характеристики
рисунок 2.7 – График мнимой частотной характеристики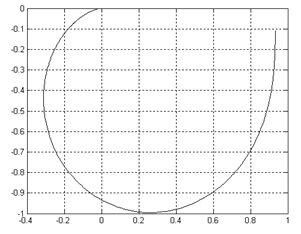

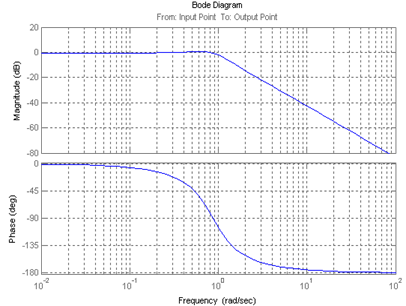

 рисунок 2.9 – Графики ЛАЧХ и ЛФЧХ
рисунок 2.9 – Графики ЛАЧХ и ЛФЧХ

