Учебная работа. Реферат: Использование дефектов, возникающих при имплантации водорода или гелия, для формирования глубинных структур в кремнии

Учебная работа. Реферат: Использование дефектов, возникающих при имплантации водорода или гелия, для формирования глубинных структур в кремнии

использование дефектов, возникающих при имплантации водорода или гелия, для формирования глубинных структур в кремнии

(реферат)

В данной работе представлены экспериментальные результаты, демонстрирующие возможность формирования различных структур в стандартных пластинах монокристаллического кремния с использованием дефектов, создаваемых имплантацией водорода или гелия.

Сформированные в результате имплантации водорода или гелия дефекты могут быть использованы для создания структур “кремний-на-оксиде” (КНО) [1-3]. Данный метод получения структур КНО основан на способности сформированного в результате имплантации водорода или гелия захороненного дефектного слоя служить центром геттерирования различных примесей, в том числе, кислорода. В наших экспериментах пластины кремния имплантировались водородом или гелием дозой 1×1015
— 4×1016
см-2
, причем энергия ионов соответствовала проективному пробегу 0,9 мкм. затем в имплантированные пластины из низкоэнергетичной плазмы вводился кислород, который геттерировался на дефектах захороненного слоя. На заключительном этапе образцы отжигались в вакууме.

Ниже приведены результаты экспериментального исследования полученных структур. Представленные на рисунке 1 профили распределения кислорода по глубине пластин, полученные методом масс-спетроскопии вторичных ионов (ВИМС), показывают, что на глубине, соответствующей захороненному слою, наблюдается накопление кислорода с концентрацией 1,4×1017
и 3,5×1017
см-2
для образцов, имплантированных водородом дозами 2×1016
и 4×1016
см-2
, соответственно. таким образом, представленный метод позволяет собирать на необходимой глубине кислород в концентрациях, приблизительно на порядок величины превышающих дозу имплантированного водорода.

Рис.1. ВИМС-профили распределения кислорода в пластинах кремния со сформированным захороненным кислородсодержащим слоем: а
— доза имплантации водорода 2×1016
см-2
, б
— доза имплантации водорода 4×1016
см-2

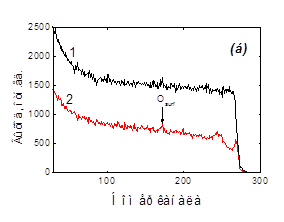
На рисунке 2 представлены результаты измерения поперечной проводимости сформированных структур. Кривые 1 измерены после имплантации водорода (до введения кислорода), кривые 2 — после проведения всех операций.

Как видно из представленных данных, сформированный в глубине пластин кислородсодержащий слой обладает изолирующими свойствами.

сопоставление графиков показывает, что сопротивление слоя и напряжения его пробоя увеличиваются с ростом дозы имплантированного водорода.

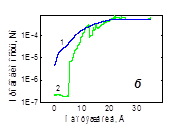
Рис.2. Электрополевые зависимости поперечной проводимости пластин кремния со сформированным захороненным кислородсодержащим слоем а
— доза имплантации водорода 2×1016
см-2
, б
— доза имплантации водорода 4×1016
см-2

Как показали проведенные исследования, реализация описанной выше последовательности технологических операций (имплантация водорода или гелия, введение кислорода из плазмы, отжиг) при определенном выборе режимов позволяет создавать в кремнии системы нанотрубок, перпендикулярных поверхности пластины. На рисунке 3 представлены СЭМ-изображения поверхности и торца пластины кремния со сформированными в ней одномерными дефектами (нанотрубками).

На рисунке 4а представлены полученные методом ВИМС профили распределения кислорода и кремния по глубине в такой структуре. Спектры резерфордовского обратного рассеяния (РОР) в случайном (кривая 1) и каналированном (кривая 2) режимах приведены на рисунке 4б. В экспериментах по РОР энергия падающих ионов составляла 2,4 МэВ, угол рассеяния — 170о
. изучение влияния переменных магнитных полей на сверхпроводники представляет не только научный, но и практический интерес. В ряде криогенных гравиинерциальных приборов на сверхпроводящие элементы их конструкций действуют магнитные поля, звукового диапазона частот 10 — 104 Гц. При этом безразлично, будет ли эта переменная составляющая действовать извне или наводиться за счет циклических движений сверхпроводника в постоянном магнитном поле. Изучение отклика сверхпроводника на подобные внешние воздействия обычно проводится индуктивными и механическими методами [1 — 3]. По величине и характеру изменения определяемых параметров обычно судят о проникновении магнитного поля, диссипативных процессах в сверхпроводнике. Для экспериментального изучения магнитомеханических эффектов используется механический метод [1, 2]. Где измеряется величина затухания (авторы обозначили символом Q-1
) и частота (f) колебаний в различных внешних условиях.

Наиболее существенные изменения частоты 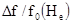[1, 2] и затухания колебаний [1] происходят в смешанном состоянии сверхпроводника [3]. Отмечено, что величины Q-1
и 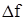зависят от квадрата частоты, кристаллической структуры сверхпроводника [5], ориентации в магнитном поле [1]. В сверхпроводнике 1 рода наблюдается ступенька при Нe
= Нk
, а в сверхпроводнике 2 рода на кривой Q-1
появляется пик.

Для объяснения наблюдаемых магнитомеханических эффектов предлагались различные модельные представления. В работе [4] введено понятие эффективной жесткости сверхпроводников, обусловленной вихрями увлекаемых деформирующейся кристаллической решеткой, с чем не согласны авторы [5, 6], поскольку зависимость частоты от поля Не
проявляется как в смешанном, так и в нормальном состоянии. С точки зрения электродинамики магнитомеханические эффекты можно рассматреть как результат воздействия на сверхпроводник переменных полей малой амплитуды, проникающих на глубину скин-слоя. В докладе рассматривается модель комплексной магнитной поляризуемости, где устанавливается связь величины αij
с комплексными проводимостью и магнитной проницаемостью сверхпроводника [7]. В высокочастотном пределе при |qd| >> 1, когда глубина скин-слоя λ превосходит лондоновскую глубину проникновения λL
,
получено:

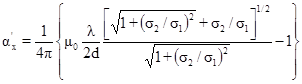, (4)

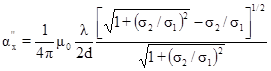. (5)

В низкочастотном пределе |qd| >> 1:

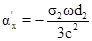, (6)

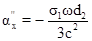, (7)

где μ0
— статическая магнитная проницаемость сверхпроводника;

σ1
и σ2
— действительная и мнимая части комплексной проводимости;

d — толщина пластины;

q — волновой вектор.

комплексная магнитная проницаемость выражается как .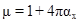

Для сверхпроводника второго рода в смешанном состоянии с закрепленными на центрах пиннинга вихрями, используя модель Гиттлемана — Розенблюма [8], получим:

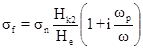, (8)

где σf
— проводимостьв смешанном состоянии; σn
— проводимость в нормальном состоянии; ωp
— пиннинговая частота.

Частоту ωp,
при которой пиннинг перестает влиять на сопротивление сверхпроводника определим 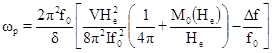[9]:

. (9)

Оценки дают

Рис.4. Профили распределения кислорода и кремния по глубине (а) и спектры РОР (б) для структуры со сформированными одномерными дефектами.

Приведенные на рисунках 3 и 4 результаты позволяют утверждать, что в приповерхностной области кремния толщиной приблизительно 1,4 мкм возникают одномерные дефекты, представляющие собой окисленные кремниевые трубки.

исследование процессов молекулярной релаксации методами колебательной спектроскопии дает богатую информацию о структурно-динамических свойствах солевой системы. такого рода исследования основаны на том факте, что ширины полос в колебательном спектре обратно пропорциональны временам молекулярной релаксации [1 — 3]. При этом каждый из релаксационных процессов дает вклад в общую ширину колебательной полосы. Молекулярная подразделяются на адиабатические и неадиабатические. Среди адиабатических наибольшее процессам относится релаксация за счет отталкивательных, диполь-дипольных и ион-дипольных взаимодействий, а также резонансный обмен колебательными квантами и внутримолекулярный распад колебательных состояний с участием фононов. В последнем случае внутримолекулярная колебательная меньшей частотой и возмущением ближайшего окружения. В свете этих рассуждений, в настоящей работе предпринята попытка, проанализировать возможные дополнительные механизмы колебательной релаксации в бинарных солевых системах с молекулярными ионами по сравнению с индивидуальными солями.

Все перечисленные выше факторы молекулярной релаксации, имеющие место в индивидуальных солях [4], актуальны и для бинарных солевых систем. Надо иметь в виду, что в бинарной солевой системе кристаллическая структура исходных солей меняется, и это может сказаться на изменении характеристик соответствующих спектральных переходов. Однако, в бинарных солевых системах, имеющих два сорта молекулярных ионов, возможен еще один релаксационный механизм, если различные молекулярные ионы имеют близкие по частотам внутримолекулярные колебания (ВМК). При этом соответствующего nj

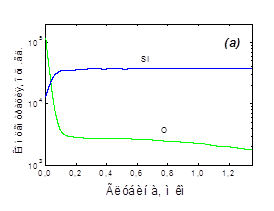
колебания молекулярного иона другого сорта, а разница энергий передаваться фононам решетки. Такой межмолекулярный фононный распад реализуется при условиях:

nj

i

, ni

— nj

m

, (1)

где nm

— максимальная частота фононного спектра. Тогда ширину d колебательной полосы бинарной солевой системы можно представить в виде [5]:

d = ddep
+ ddd
+ did
+ drep
+ dres
+ dimp
+ demp
+ dor
, (2)

где ddep
— вклад в ширину спектральной линии за счет колебательной дефазировки; ddd
, did
, drep
— вклады за счет диполь-дипольных, ион-дипольных, отталкивательных взаимодействий; dres
— вклад за счет резонансной передачи колебательных квантов; dimp
— вклад за счет процессов внутримолекулярного фононного распада колебательно-возбужденных состояний, demp
— вклад в ширину спектральной линии за счет процессов межмолекулярного фононного распада колебательно-возбужденных состояний.

Целью настоящей работы является сравнение процессов молекулярной релаксации в бинарных солевых системах, для которых выполняется условие (1), и в индивидуальных солях, а также выявление возможных дополнительных механизмов релаксации колебательно-возбужденных состояний молекулярных ионов.

В соответствии с целью в качестве объектов исследования выбраны следующие эквимолярные бинарные солевые системы: нитрат калия — сульфат натрия (KNO3
— Na2
SO4
), нитрат натрия — сульфат натрия (NaNO3
— Na2
SO4
) и нитрат натрия — ацетат натрия (NaNO3
— NaCH3
COO). Система KNO3
— Na2
SO4
приготавливалась смешиванием мелкодисперсного порошка сульфата натрия с расплавом нитрата калия при температуре 620 ¸ 630 К, а затем медленно охлаждалась непосредственно во вращающемся тигле. системы NaNO3
— Na2
SO4
и NaNO3
— NaCH3
COO приготавливались аналогично. При этом температура расплава нитрата натрия составляла 590 ¸ 600 К.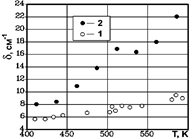

Рис.5. Температурная зависимость ширины контура n1
(A) колебания NO3
—
в кристалле KNO3
(1
) и в системе KNO3
— Na2
SO4
(2
).

Рис.6. Температурная зависимость ширины контура n1
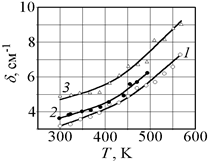
(A) колебания NO3
—
в кристалле NaNO3
(1
), а также в системах NaNO3
— NaCH3
COO (2
) и NaNO3
— Na2
SO4
(3
).

В этих системах для полносимметричного валентного колебания n1
»1050¸1070 см-1
аниона NO3
—
выполняется условие (1), так как полносимметричное валентное колебание n1
(SO4
2-
) аниона SO4
2-
и валентное колебание n (C-C) связи C-C аниона CH3
COO-
локализованы в области 990¸1000 cм-1
и 930 cм-1
соответственно [6]. В таких системах, в принципе, возможна диссипация колебательной энергии ВМК нитрат-иона с последующим возбуждением соответствующего ВМК сульфат-иона или ацетат-иона и рождением решеточного фонона. В системе нитрат — сульфат разница в частотах указанных ВМК составляет примерно 60¸70 см-1
, а для системы нитрат — ацетат около 120¸140 см-1
. Эти значения попадают в область достаточно высокой плотности фононного спектра исследуемых кристаллов [7, 8].

Спектры КР регистрировались спектрометром ДФС-24 в области валентных полносимметричных колебаний n1
(A) нитрат-иона NO3
—
и n1
(A) сульфат-иона SO4
2-
, а также валентного колебания n (C-C) связи C-C ацетат-иона CH3
COO-
от 850 до 1150 см-1
в интервале температур 298 ¸ 587 K. Положения максимумов колебательных полос фиксировалось с точностью ±0.5 см-1
, а их ширины — с точностью ±0.1 см-1
. температура образцов поддерживалась в процессе регистрации спектров с точностью ±0.5 К. методика регистрации и обработки спектров КР подробно описана в [9-11]. спектры рассматриваемых колебаний резкополяризованы и их формирование можно приписать процессам колебательной релаксации.

На рис.1 представлена температурная зависимость ширины d контура n1
(A) колебания NO3
—
в кристалле KNO3
(1
) и в бинарной системе KNO3
— Na2
SO4
(2
). сравнение ширины контура n1
колебания NO3
—
в бинарной смеси с соответствующими данными для кристалла KNO3
показывает, что их величины и скорость температурного уширения значительно выше в спектре КР системы KNO3
— Na2
SO4
. Можно констатировать, что в бинарной системе имеют место факторы, способствующие увеличению скорости колебательной релаксации моды n1
аниона NO3
—
по сравнению с индивидуальной солью. По нашему мнению, объяснение данному факту можно найти, если допустить наличие сильного взаимодействия между разными анионами с близкими частотами ВМК, при котором реализуется механизм фононного распада по выше указанной схеме.

На рис.2 представлена температурная зависимость ширины d контура n1
(A) колебания NO3
—
в кристалле NaNO3
(1
), а также в бинарных системах NaNO3
— NaCH3
COO (2
) и NaNO3
— Na2
SO4
(3
). Как видно, скорость релаксации (пропорциональная ширине d) колебания n1
(A) аниона NO3
—
в бинарной системе больше, чем в кристаллах NaNO3
. Это можно объяснить наличием в бинарной солевой системе дополнительного механизма релаксации колебания n1
(A) нитрат-иона, связанного с возбуждением полносимметричного колебания аниона SO4
2-
или валентного колебания n (C-C) аниона CH3
COO-
и «рождением» решеточного фонона. Возможность такого механизма релаксации обусловлена тем, что разница в частотах между колебанием n1
(A) нитрат-иона (1070 см-1
), с одной стороны, и колебаниями n1
(A) сульфат-иона (1000 см-1
) и n (C-C) ацетат-иона (930 см-1
), с другой стороны, отвечает фононному спектру соответствующих кристаллов. В пользу предложенного механизма релаксации говорит и тот факт, что разница (1.5¸2 см-1
) между ширинами спектральной линии моды n1
(A) NO3
—
в NaNO3
и в NaNO3
— Na2
SO4
больше, чем соответствующая разница (0.5 см-1
) в NaNO3
и в NaNO3
— NaCH3
COO. Этот факт представляется весьма естественным, так как разница частот колебаний в случае системы NaNO3
— Na2
SO4
(70 см-1
) оказывается в области большей плотности состояний фононного спектра, чем соответствующая разница для системы NaNO3
— NaCH3
COO (140 см-1
).

таким образом, в бинарных солевых системах, в принципе, возможен квазирезонансный обмен колебательными квантами между различными молекулярными ионами с близкими значениями частот ВМК. поэтому увеличение скорости колебательной релаксации моды n1
(A) NO3
—
в бинарной солевой системе, по сравнению с индивидуальной солью, следует связать с близкодействующими обменными взаимодействиями анионов, при которых диссипация колебательной энергии нитрат-иона сопровождается переходом SO4
2-
или CH3
COO-
в колебательно возбужденное состояние и «рождением» решеточного фонона.

причиной формирования наблюдаемых одномерных дефектов является способность инкорпорированного в кремний водорода или гелия выходить к поверхности пластины, создавая при этом одномерные дефектные области. В процессе последующего введения кислорода из плазмы происходит их окисление, в результате чего в пластине и формируется система оксидных нанотрубок.

Литература

1. А.В. Раков. Труды ФИАН СССР, 27 (1964).

2. К.А. Валиев, Е.Н. Иванов. Успехи физических наук 109, 1
, 31 (1973).

3. К. Сарка, С.А. Кириллов. Украинский физический журнал, 26, 7
, 1118 (1981).

4. A. R. Aliev, M. M. Gafurov, I. R. Akhmedov. Chemical Physics Letters 378, 1-2
, 155 (2003).

5. А.Р. Алиев, М.М. Гафуров. журнал физической химии, 79, 6
, 1087 (2005).

6. К. Кольрауш. Спектры комбинационного рассеяния. М.: ИЛ, 1952. С.229.

7. D. W. James, W. H. Leong. Journal of Chemical Physics 49, 11
, 5089 (1968).

8. E. Cazzanelli, R. Frech. Journal of Chemical Physics 81, 11
, 4729 (1984).

9. А.Р. Алиев, А.З. Гаджиев. журнал прикладной спектроскопии 59, 5-6
, 465 (1993).

10. A. R. Aliev, M. M. Gafurov. Molecular Physics 100, 21
, 3385 (2002).

11. A. R. Aliev, M. M. Gafurov, I. R. Akhmedov. ChemicalPhysicsLetters 353, 3-4
, 270 (2002).