Загрузка...
Учебная работа. Реферат: Двойной интеграл в полярных координатах
Пусть в двойном интеграле
(1)
при обыденных догадках мы хотим перейти к полярным координатам r и f, полагая
x = r cos j, y = r sin j. (2)
Область интегрирования S разобьем на простые ячейки DSi при помощи координатных линий r = ri (окружности) и j = ji (лучи) (рис.1).
Введем обозначения:
Drj = rj+1 — rj,
Dji = ji+1 — ji
Потому что окружность перпендикулярна (ортогональна) радиусам, то внутренние ячейки DSi с точностью до нескончаемо малых высшего порядка малости относительно их площади можно разглядывать как прямоугольники с измерениями rjDji и Drj; потому площадь каждой таковой ячейки будет равна:
DSi = rj Dji Drj (3)
Что касается ячеек DSij неверной формы, примыкающих к границе Г области интегрирования S, то эти ячейки не воздействую на
В качестве точки Mij$Sij для простоты выберем верхушку ячейки DSij с полярными координатами rj и ji. Тогда декартовые координаты точки Mij равны:
xij = rj cos ji, yij = rj sin ji.
Иследовательно,
f(xij,yij) = f(rj cos ji, rj sin ji) (3′)
Двойной интеграл (1) представляет собой предел двумерной интегральной суммы, при этом можно показать, что на
интегральной суммы, являющиеся нескончаемо малыми высшего порядка малости, потому беря во внимание формулы (3) и (3′),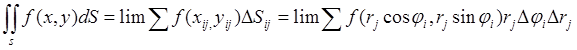 
получаем:
(4)
где d — наибольший поперечник ячеек DSij и сумма всераспространена на все ячейки обозначенного выше вида, полностью находящиеся в области S. С иной стороны, величины ji и rj сущность числа и их можно разглядывать как прямоугольные декартовые координаты неких точек плоскости Ojr. Таковым образом, сумма (4) является интегральной суммой для функции
f(r cosj, r sinj)r,
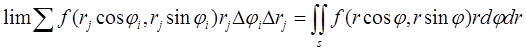
соответственная прямоугольной сетке с линейными элементами Dji и Dri. Как следует
(5)
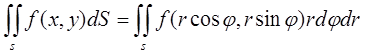
Сравнивая формулы (4) и (5), получим совсем
(6)
Выражение
dS = rdjdr
именуется двумерным элементом площади в полярных координатах. Итак, чтоб в двойном интеграле (1) перейти к полярным координатам, довольно координаты x и y поменять по формулам (2), а заместо элемента площади dS подставить выражение (7).
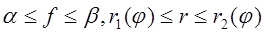
Для вычисления двойного интеграла (6) его необходимо поменять повторным. Пусть область интегрирования S определяется неравенствами
Где r1(j), r1(j) — конкретные непрерывные функции на отрезке [a,b]. (рис 2).
Имеем
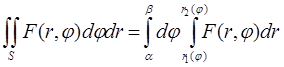
(8)
Где
F(r,j) = rf(rcosj, rsinj)
Пример 1.
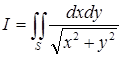
Переходя к полярным координатам j и r, вычислить двойной интеграл
Где S — 1-ая четверть круга радиуса R=1, с центром в точке О(0,0) (рис 3).
Потому что
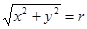
то применяя формулу (6),
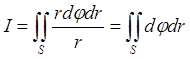
получим
Область S определена
Неравенствами
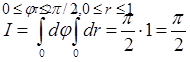
Потому на основании формулы (8) имеем
Пример 2.
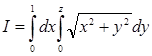
В интеграле
(9)
перейти к полярным координатам.
Область интегрирования тут есть треугольник S, ограниченный прямыми y=0, y=x, x=1 (рис 4).
В полярных координатах уравнения
этих прямых записываются
последующим образом: j=0,
j=p/4, rcosj=1 и,
как следует, область S
определяется неравенствами
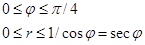
Отсюда на основании формул
(6) и(8), беря во внимание, что
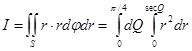
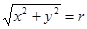
имеем
]]>