Учебная работа. Реферат: Единая теория поля
Единая теория поля -это физическая теория, задачей которой является единое описание всех простых частиц (либо хотя бы группы частиц), выведение параметров этих частиц, законов их движения, их обоюдных перевоплощений из некоторых всепригодных законов, описывающих единую «первоматерию», разные состояния которой и соответствуют разным частичкам.
Первым примером Единой теории поля была попытка Х. А. Лоренца разъяснить всю инерцию электрона (т. е. вывести законы в итоге должны были сводиться к законам, описывающим это поле. Последовательное проведение данной для нас программки оказалось неосуществимым, но сама попытка «примирить» дискретное (электрон рассматривался как вещественная точка) и непрерывное (электромагнитное поле), попытка одного описания различных базовых видов материи возобновлялась и в наиболее позже время.
Развитие квантовых представлений показало, что задачка состоит не в том, чтоб «примирить» частички и поля, дискретное и непрерывное. Любые «частички» и «поля» имеют двоякую природу, объединяя внутри себя как характеристики корпускул, так и характеристики волн. Но при всем этом любой из видов «волно-частиц» владеет своими персональными качествами, своими специфичными законами движения. У электрона эти законы остальные, чем, к примеру, у нейтрино либо фотона. Открытие каждой новейшей «простой частички» рассматривается в современной теории как обнаружение новейшего типа материи. По мере того как раскрывались новейшие частички (а так как все частички имеют и волновые характеристики, можно сказать: новейшие типы полей), всё настоятельнее становилась Потребность осознать, почему их настолько не мало (на данный момент уже наиболее двухсотен), разъяснить их характеристики и расшифровать, в конце концов, что значит само слово «простая» применительно к частичке. опять — уже на наиболее высочайшем уровне — возникли пробы одного описания материи.
Огромную стимулирующую роль сыграла тут общая теория относительности А.Эйнштейна. В данной для нас теории и законы тяготения, и уравнения движения притягивающихся масс получаются как следствие общих законов, определяющих гравитационное поле. Общая теория относительности связывает гравитацию с геометрическими качествами пространства-времени. В неких работах делались пробы наиболее широкой «геометризации» теории, т. е. вводились такие догадки, касающиеся геометрии, которые дозволили бы включить в рассмотрение и электромагнитные поля, также учитывать квантовые эффекты. Таковой «геометрический» подход весьма привлекателен, но пока в этом направлении значительно продвинутся не удалось.
совсем новейший подход — его можно именовать модельным — ведёт своё начало от работ Л. де Бройля по нейтринной теории света. В этих работах предполагается, что фотоны — кванты света — представляют собой пары «слившихся» нейтрино (отсюда заглавие — «теория слияния»). Нейтрино не имеет электронного заряда, его масса покоя равна нулю и спин равен 1/2 (в единицах неизменной Планка). Сливаясь, два нейтрино могут образовать нейтральную частичку с нулевой массой и спином 1, т. е. с чертами фотона.
Нейтринная теория света, хотя и не вольная от недочетов, была первой в ряду моделей составных частиц. Посреди их — модель Э. Ферми и Ян Чженьнина, рассматривающая p-мезон как связанное состояние нуклона и антинуклона, модель Сёити Саката (Япония), М. А. Маркова и Л. Б. Окуня, в какой все очень взаимодействующие частички строились из трёх базовых частиц, и др.
Особое распространение в крайние годы получила модель кварков, предложенная в первый раз (1964) М. Гелл-Маном и Г. Цвейгом. Согласно данной для нас модели, все очень взаимодействующие частички (мезоны, барионы, резонансные частички) состоят из особенных «субчастиц» с дробными электронными зарядами — из кварков трёх типов, также соответственных античастиц (антикварков). Эта модель, оказавшаяся очень плодотворной для систематики простых частиц и объяснившая ряд тонких эффектов, связанных с массами частиц, их магнитными моментами, и некие др. экспериментальные факты, резко понижает число претендентов на звание «поистине простых» частиц и, как следует, в известной мере решает задачку одного описания материи. Но теория ещё далека от нужной ясности, равно как и тесту надлежит ответить на ряд кардинальных вопросцев. Довольно сказать, что кварки в вольном состоянии ещё не обнаружены и не исключено, что это нереально в принципе. В этом случае кварковая модель растеряет собственный смысл как составная модель.
Ещё до сотворения кварковой модели В. Гейзенберг (1957) начал развивать теорию, в какой за базу принимается всепригодное единое поле, описываемое величинами, которые в арифметике именуются спинорами; потому теория получила заглавие единой нелинейной спинорной теории. В отличие от описанной чуть повыше теории слияния это базовое, описывающее «материю в целом» поле не связывается конкретно ни с какой настоящей частичкой. 2-ое существенное отличие основного уравнения теории Гейзенберга — нелинейность, отражающая взаимодействия фундаментального поля с самим собой. Математически это выражается в возникновении в уравнении движения членов, пропорциональных не самой, описывающей поле величине, а хорошей от единицы её степени. Как и в общей теории относительности, благодаря данной для нас нелинейности уравнения движения настоящих частиц должны получаться из основного уравнения. Из этого же уравнения должны вытекать значения масс, электронных зарядов, спинов и др. черт частиц.
Математическое исследование уравнения Гейзенберга представляет собой тяжелую задачку, которую пока удалось решить только в достаточно грубом приближении. Наиболее того, до сего времени ещё не подтверждена самосогласованность процедуры устранения бесконечностей в теории Гейзенберга. вкупе с тем количественные результаты, приобретенные в данной для нас теории, кажутся обнадёживающими и общая программка нелинейной Единой теории поля продолжает считаться многообещающей.
Таковым образом, Единая теория поля ещё не построена. Но неразрывная связь меж всеми частичками, всепригодная обоюдная превращаемость частиц, всё наиболее явственно проявляющиеся черты единства материи принуждают находить пути перехода от современной квантовой теории поля, ограничивающейся констатацией обилия форм материи, к единой теории, которая призвана это обилие разъяснить.
Больщое воздействие на развитие Теоирии одного поля оказала Теория тяготения Эйнштейна. Какова же основная мысль данной для нас теории?
Для того чтоб имитировать, к примеру, сферическое поле тяготения Земли, необходимы ускоренные системы с разным направлением убыстрения в разных точках. Наблюдатели в различных системах, установив меж собой связь, найдут, что они движутся ускоренно друг относительно друга, и тем установят отсутствие настоящего поля тяготения. Таковым образом, настоящее поле тяготения не сводится просто к введению ускоренной системы отсчёта в обыкновенном пространстве, либо, говоря поточнее, в пространстве-времени специальной теории относительности. Но Эйнштейн показал, что если, исходя из принципа эквивалентности, востребовать, чтоб настоящее гравитационное поле было эквивалентно локальным подходящим образом ускоренным в каждой точке системам отсчёта, то в хоть какой конечной области пространство-время окажется искривленным — неевклидовым. Это значит, что в трёхмерном пространстве геометрия, совершенно говоря, будет неевклидовой (сумма углов треугольника не равна p, отношение длины окружности к радиусу не равно 2p и т.д.), а время в различных точках будет течь по-разному. Таковым образом, согласно теории тяготения Эйнштейна, настоящее гравитационное поле является не чем другим, как проявлением искривления (отличия геометрии от евклидовой) четырёхмерного пространства-времени.
Следует выделить, что создание теории тяготения Эйнштейна сделалось вероятным лишь опосля открытия неевклидовой геометрии русским математиком Н. И. Лобачевским, венгерским математиком Я. Больяй, германскими математиками К. Гауссом и Б. Риманом.
В отсутствие тяготения движение тела по инерции в пространстве-времени специальной теории относительности изображается прямой линией, либо, на математическом языке, экстремальной (геодезической) линией. Мысль Эйнштейна, основанная на принципе эквивалентности и составляющая базу теории тяготения, состоит в том, что и в поле тяготения все тела движутся по геодезическим линиям в пространстве-времени, которое, но, искривлено, и, как следует, геодезические полосы уже не прямые.
Массы, создающие поле тяготения, искривляют пространство-время. Тела, которые движутся в искривленном пространстве-времени, и в этом случае движутся по одним и этим же геодезическим линиям независимо от массы либо состава тела. Наблюдающий принимает это движение как движение по искривленным траекториям в трёхмерном пространстве с переменной скоростью. Но с самого начала в теории Эйнштейна заложено, что искривление линии движения, законконфигурации скорости — это характеристики пространства-времени, характеристики геодезических линий в этом пространстве-времени, а как следует, убыстрение всех разных тел обязано быть идиентично и, означает, отношение тяжёлой массы к инертной [от которого зависит убыстрение тела в данном поле тяготения, см. формулу (6)] идиентично для всех тел, и эти массы неотличимы. Таковым образом, поле тяготения, по Эйнштейну, есть отклонение параметров пространства-времени от параметров плоского (не искривлённого) обилия специальной теории относительности.
2-ая принципиальная мысль, лежащая в базе теории Эйнштейна, — утверждение, что тяготение, другими словами искривление пространства-времени, определяется не только лишь массой вещества, слагающего тело, да и всеми видами энергии, присутствующими в системе. Эта мысль явилась обобщением на вариант теории тяготения принципа эквивалентности массы (m) и энергии (Е) специальной теории относительности, выражающейся формулой Е = mс2. Согласно данной для нас идее, тяготение зависит не только лишь от распределения масс в пространстве, да и от их движения, от давления и натяжений, имеющихся в телах, от электромагнитного поля и всех др. физических полей.
В конце концов, в теории тяготения Эйнштейна обобщается вывод специальной теории относительности о конечной скорости распространения всех видов взаимодействия. Согласно Эйнштейну, конфигурации гравитационного поля распространяются в вакууме со скоростью с.
Уравнения тяготения Эйнштейна
В специальной теории относительности в инерциальной системе отсчета квадрат четырёхмерного «расстояния» в пространстве-времени (интервала ds) меж 2-мя нескончаемо близкими событиями записывается в виде:
ds2= (cdt)2 — dx2- dy2 — dz2 (7)
где t — время, х, у, z — прямоугольные декартовы (пространственные) координаты. Эта система координат именуется галилеевой. Выражение (7) имеет вид, аналогичный выражению для квадрата расстояния в евклидовом трёхмерном пространстве в декартовых координатах (с точностью до числа измерений и символов перед квадратами дифференциалов в правой части). Такое пространство-время именуют плоским, евклидовым, либо, поточнее, псевдоевклидовым, подчёркивая особенный нрав времени: в выражении (7) перед (cdt)2 стоит символ «+», в отличие от символов «—» перед квадратами дифференциалов пространственных координат. Таковым образом, особая теория относительности является теорией физических действий в плоском пространстве-времени (пространстве-времени Минковского).
В пространстве-времени Минковского не непременно воспользоваться декартовыми координатами, в каких интервал записывается в виде (7). Можно ввести любые криволинейные координаты. Тогда квадрат интервала ds2 будет выражаться через эти новейшие координаты общей квадратичной формой:
ds2 = gikdx idx k (8)
(i, k = 0, 1, 2, 3), где x 1, x 2, x 3— произвольные пространств, координаты, x0 = ct — временная координата (тут и дальше по два раза встречающимся индексам делается суммирование). С физической точки зрения переход к произвольным координатам значит и переход от инерциальной системы отсчёта к системе, совершенно говоря, передвигающейся с убыстрением (причём в общем случае различным в различных точках), деформирующейся и вращающейся, и внедрение в данной для нас системе не декартовых пространственных координат. Невзирая на кажущуюся сложность использования таковых систем, фактически они время от времени оказываются комфортными. Но в специальной теории относительности постоянно можно воспользоваться и галилеевой системой, в какой интервал записывается в особенности просто. [В этом случае в формуле (8) gik= 0 при i ¹ k, g00 = 1, gii = —1 при i = 1, 2, 3.]
В общей теории относительности пространство-время не плоское, а искривленное. В искривленном пространстве-времени (в конечных, не малых, областях) уже недозволено ввести декартовы координаты, и внедрение криволинейных координат становится неминуемым. В конечных областях такового искривленного пространства-времени ds2 записывается в криволинейных координатах в общем виде (8). Зная gik как функции четырёх координат, можно найти все геометрические характеристики пространства-времени. Молвят, что величины gik определяют метрику пространства-времени, а совокупа всех gik именуют метрическим тензором. При помощи gik рассчитываются темп течения времени в различных точках системы отсчёта и расстояния меж точками в трёхмерном пространстве. Так, формула для вычисления нескончаемо малого интервала времени dt по часам, покоящимся в системе отсчёта, имеет вид:

При наличии поля тяготения величина g00 в различных точках различная, как следует, темп течения времени зависит от поля тяготения. Оказывается, что чем посильнее поле, тем медлительнее течёт время по сопоставлению со временем для наблюдающего вне поля.
Математическим аппаратом, изучающим неевклидову геометрию в случайных координатах, является тензорное исчисление. Общая теория относительности употребляет аппарат тензорного исчисления, её законы записываются в случайных криволинейных координатах (это значит, а именно, запись в случайных системах отсчёта), как молвят, в ковариантном виде.
Основная задачка теории тяготения — определение гравитационного поля, что соответствует в теории Эйнштейна нахождению геометрии пространства-времени. Эта крайняя задачка сводится к нахождению метрического тензора gik.
Уравнения тяготения Эйнштейна связывают величины gik с величинами, характеризующими материю, создающую поле: плотностью, потоками импульса и т.п. Эти уравнения записываются в виде:
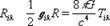
(9)
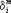
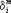
тут Rik — так именуемый тензор Риччи, выражающийся через gik, его 1-ые и 2-ые производные по координатам; R = Rik g ik (величины g ik определяются из уравнений gikg km = , где — знак Кронекера); Tik — так именуемый тензор энергии-импульса материи, составляющие которого выражаются через плотность, потоки импульса и др. величины, характеризующие материю и её движение (под физической материей предполагаются обыденное вещество, электромагнитное поле, все др. физические поля).
Скоро опосля сотворения общей теории относительности Эйнштейн показал (1917), что существует возможность конфигурации уравнений (9) с сохранением главных принципов новейшей теории. Это изменение состоит в добавлении к правой части уравнений (9) так именуемого «космологического члена»: Lgik. Неизменная L, именуется «космологической неизменной», имеет размерность см-2. Целью этого усложнения теории была попытка Эйнштейна выстроить модель Вселенной, которая не меняется со временем. Космологический член можно разглядывать как величину, описывающую плотность энергии и давление (либо натяжение) вакуума. Но скоро (в 20-х гг.) русский математик А. А. Фридман показал, что уравнения Эйнштейна без L-члена приводят к эволюционирующей модели Вселенной, а южноамериканский астролог Э. Хаббл открыл (1929) законтак именуемого красноватого смещения для галактик, которое было истолковано как доказательство эволюционной модели Вселенной. Мысль Эйнштейна о статической Вселенной оказалась неправильной, и хотя уравнения с L-членом тоже допускают нестационарные решения для модели Вселенной, необходимость в L-члене отпала. Опосля этого Эйнштейн пришел к выводу, что введение L-члена в уравнения тяготения не необходимо (другими словами что L = 0). Не все физики согласны с сиим заключением Эйнштейна. Но следует выделить, что пока нет никаких серьёзных наблюдательных, экспериментальных либо теоретических оснований считать L хорошим от нуля. Во всяком случае, если L ¹ 0, то, согласно астрофизическим наблюдениям, его абсолютная величина очень мала: |L|< 10-55 см-2. Он может играться роль лишь в космологии и фактически совсем не сказывается во всех др. задачках теории тяготения. Всюду в предстоящем будет положено L = 0.
Снаружи уравнения (9) подобны уравнению для ньютоновского потенциала. В обоих вариантах слева стоят величины, характеризующие поле, а справа — величины, характеризующие материю, создающую поле. Но уравнения (9) имеют ряд существенных особенностей. Уравнение ньтоновского потенциала линейно и потому удовлетворяет принципу суперпозиции. Оно дозволяет вычислить гравитационный потенциал j для хоть какого распределения произвольно передвигающихся масс. Ньютоновское поле тяготения не зависит от движения масс, потому уравнение Ньтона само не описывает конкретно их движение. Движение масс определяется из второго закона механики Ньютона. Другая ситуация в теории Эйнштейна. Уравнения (9) не линейны, не удовлетворяют принципу суперпозиции. В теории Эйнштейна недозволено произвольным образом задать правую часть уравнений (Tik), зависящую от движения материи, а потом вычислить гравитационное поле gik. Решение уравнений Эйнштейна приводит к совместному определению и движения материи, создающей поле, и к вычислению самого поля. Значительно при всем этом, что уравнения поля тяготения содержат внутри себя и уравнения движения масс в поле тяготения. С физической точки зрения это соответствует тому, что в теории Эйнштейна движение материи, создающей искривление. Очевидно, для решения уравнений Эйнштейна нужно знать свойства материи, которые не зависят от гравитационных сил. Так, к примеру, в случае безупречного газа нужно знать уравнение состояния вещества — связь меж давлением и плотностью.
В случае слабеньких гравитационных полей метрика пространства-времени не достаточно различается от евклидовой и уравнения Эйнштейна приближённо перебегают в уравнения нютоновского потенциала и второго закона Ньютона (если рассматриваются движения, неспешные по сопоставлению со скоростью света, и расстояния от источника поля много меньше, чем l = сt, где t — свойственное время конфигурации положения тел в источнике поля). В этом случае можно ограничиться вычислением малых поправок к уравнениям Ньютона. Эффекты, надлежащие сиим поправкам, разрешают экспериментально проверить теорию Эйнштейна (см. ниже). В особенности существенны эффекты теории Эйнштейна в мощных гравитационных полях.
Некие выводы теории тяготения Эйнштейна
Ряд выводов теории Эйнштейна отменно различается от выводов ньютоновской теории тяготения Важные из их соединены с появлением «темных дыр», сингулярностей пространства-времени (мест, где формально, согласно теории, обрывается существование частиц и полей в обыкновенной, известной нам форме) и существованием гравитационных волн.
Чёрные дыры. Согласно теории Эйнштейна, 2-ая галлактическая скорость в сферическом поле тяготения в пустоте выражается той же формулой, что и в теории Ньютона:
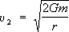
(10)
Как следует, если тело массы т сожмётся до линейных размеров, наименьших величины r =2 Gm/c2, именуемой гравитационным радиусом, то поле тяготения становится так мощным, что даже свет не может уйти от него на бесконечность, к далёкому наблюдающему; для этого потребовалась бы скорость больше световой. Такие объекты получили заглавие чёрных дыр. Наружный наблюдающий никогда не получит никакой инфы из области снутри сферы радиуса r = 2Gm/с2. При сжатии вращающегося тела поле тяготения, согласно теории Эйнштейна, различается от поля не вращающегося тела, но вывод о образовании чёрной дыры остаётся в силе.
В области размером меньше гравитационного радиуса никакие силы не могут удержать тело от предстоящего сжатия. Процесс сжатия именуется гравитационным коллапсом. При всем этом вырастает поле тяготения — возрастает искривлённость пространства-времени. Подтверждено, что в итоге гравитационного коллапса безизбежно возникает сингулярность пространства-времени, сплетенная, по-видимому, с появлением его нескончаемой искривлённости. (О ограниченности применимости теории Эйнштейна в таковых критериях см. последующий раздел.) Теоретическая астрофизика предвещает появление чёрных дыр в конце эволюции мощных звёзд; может быть существование во Вселенной чёрных дыр и др. происхождения. Чёрные дыры, по-видимому, открыты в составе неких двойных звёздных систем.
Гравитационные волны. Теория Эйнштейна предвещает, что тела, передвигающиеся с переменным убыстрением, будут источать гравитационные волны. Гравитационные волны являются распространяющимися со скоростью света переменными полями приливных гравитационных сил. Таковая волна, падая, к примеру, на пробные частички, расположенные перпендикулярно направлению её распространения, вызывает повторяющиеся конфигурации расстояния меж частичками. Но даже в случае циклопических систем небесных тел излучение гравитационных волн и уносимая ими энергия ничтожны. Так, мощность излучения за счёт движения планет Солнечной системы составляет около 1011 эрг/сек, что в 1022 раз меньше светового излучения Солнца. Настолько же слабо гравитационные волны ведут взаимодействие с обыкновенной материей. Сиим разъясняется, что гравитационные волны до сего времени не открыты экспериментально.
Квантовые эффекты. Ограничения применимости теории тяготения Эйнштейна
Теория Эйнштейна — не квантовая теория. Тут она подобна традиционной электродинамике Максвелла. Но более общие рассуждения демонстрируют, что гравитационное поле обязано подчиняться квантовым законам буквально так же, как и электромагнитное поле. В неприятном случае появились бы противоречия с принципом неопределённости для электронов, фотонов и т.д. Применение квантовой теории к гравитации указывает, что гравитационные волны можно разглядывать как поток квантов — «гравитонов», которые так же настоящи, как и кванты электромагнитного поля — фотоны. Гравитоны представляют собой нейтральные частички с нулевой массой покоя и со спином, равным 2 (в единицах Планка неизменной).

В подавляющем большинстве мыслимых действий во Вселенной и в лабораторных критериях квантовые эффекты гравитации очень слабы, и можно воспользоваться не квантовой теорией Эйнштейна. Но квантовые эффекты должны стать очень существенными поблизости сингулярностей поля тяготения, где искривления пространства-времени весьма значительны. Теория размерностей показывает, что квантовые эффекты в гравитации стают определяющими, когда радиус кривизны пространства-времени (расстояние, на котором появляются значительные отличия от геометрии Евклида: чем меньше этот радиус, тем больше кривизна) становится равным величине rпл= . Расстояние rпл именуется планковской длиной; оно ничтожно не достаточно: rпл = 10-33 см. В таковых критериях теория тяготения Эйнштейна неприменима.
Сингулярные состояния появляются в процессе гравитационного коллапса; сингулярность в прошедшем была в расширяющейся Вселенной. Поочередной квантовой теории тяготения, применимой и в сингулярных состояниях, пока не существует.
Квантовые эффекты приводят к рождению частиц в поле тяготения чёрных дыр. Для чёрных дыр, возникающих из звёзд и имеющих массу, сравнимую с солнечной, эти эффекты пренебрежимо малы. Но они могут быть важны для чёрных дыр малой массы (меньше 1015 г), которые в принципе могли возникать на ранешних шагах расширения Вселенной.
Экспериментальная проверка теории Эйнштейна
В базе теории тяготения Эйнштейна лежит принцип эквивалентности. Его проверка с может быть большей точностью является важной экспериментальной задачей. Согласно принципу эквивалентности, все тела независимо от их состава и массы, все виды материи должны падать в поле тяготения с одним и этим же убыстрением. Справедливость этого утверждения, как уже говорилось, была в первый раз установлена Галилеем. Венгерский физик Л. Этвеш при помощи крутильных весов обосновал справедливость принципа эквивалентности с точностью до 10-8; южноамериканский физик Р. Дикке с сотрудниками довёл точность до 10-10, а русский физик В. Б. Брагинский с сотрудниками — до 10-12.
иной проверкой принципа эквивалентности является вывод о изменении частоты n света при его распространении в гравитационном поле. Теория предвещает изменение частоты Dn при распространении меж точками с разностью гравитационных потенциалов j1 — j2:
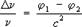
(11)
Опыты в лаборатории подтвердили эту формулу с точностью по последней мере до 1% .
Не считая этих тестов по проверке основ теории, существует ряд опытнейших проверок её выводов. Теория предвещает искривление луча света при прохождении поблизости тяжёлой массы. Аналогичное отклонение следует и из ньютоновской теории тяготения, но теория Эйнштейна предвещает в два раза больший эффект. Бессчетные наблюдения этого эффекта при прохождении света от звёзд поблизости Солнца (во время полных солнечных затмений) подтвердили пророчество теории Эйнштейна (отклонение на 1,75’’ у края солнечного диска) с точностью около 20%. Еще большая точность была достигнута при помощи современной техники наблюдения инопланетных точечных радиоисточников. Сиим способом пророчество теории доказано с точностью (на 1974) не наименьшей 6%.
Др. эффектом, тесновато связанным с предшествующим, является большая продолжительность времени распространения света в поле тяготения, чем это дают формулы без учёта эффектов теории Эйнштейна. Для луча, проходящего поблизости Солнца, эта доборная задержка составляет около 2×10-4 сек. Опыты проводились при помощи радиолокации планет Меркурий и Венера во время их прохождения за диском Солнца, также при помощи ретрансляции радиолокационных сигналов галлактическими кораблями. Пророчества теории доказаны (на 1974) с точностью 2%.
В конце концов, ещё одним эффектом является предсказываемый теорией Эйнштейна неспешный доп (не объясняемый гравитационными возмущениями со стороны др. планет Галлактики) поворот эллиптических орбит планет, передвигающихся вокруг Солнца. Самую большую величину этот эффект имеет для орбиты Меркурия — 43’’ в столетие. Это пророчество доказано экспериментально, согласно современным данным, с точностью до 1%.
Таковым образом, все имеющиеся экспериментальные данные подтверждают корректность как положений, лежащих в базе теории тяготения Эйнштейна, так и её наблюдательных пророчеств.
Следует выделить, что опыты свидетельствуют против попыток выстроить остальные теории тяготения, хорошие от теории Эйнштейна.
В заключение отметим, что косвенным доказательством теории тяготения Эйнштейна является наблюдаемое расширение Вселенной, на теоретическом уровне предсказанное на базе общей теории относительности русским математиком А. А. Фридманом посреди 20-х гг. нашего столетия.
]]>

