Учебная работа. Курсовая работа: Исследование распределения температуры в тонком цилиндрическом стержне
Исполнитель: Солнцев П.В.
Санкт-Петербургский Муниципальный Технологический Институт (технический Институт)
Санкт-Петербург 2001
Введение
В решении хоть какой прикладной задачки можно выделить три главных шага: построение математической модели исследуемого объекта, выбор метода и метода решения приобретенной модели, численная реализация метода.
Цель данной работы – на примере исследования распределения температуры в узком цилиндрическом стержне освоить главные способы приближённых вычислений, приобрести практические способности самостоятельных исследовательских работ, значительно опирающихся на внедрение способов прикладной арифметики.
Постановка задачки
Физическая модель
В ряде практических задач возникает необходимость исследования распределения температуры вдоль узкого цилиндрического стержня, помещённого в высокотемпературный поток воды либо газа. Это исследование может проводиться или на базе обработки опыта (измерение температуры в разных точках стержня), или путём анализа соответственной математической модели.
В истинной работе употребляются оба подхода.
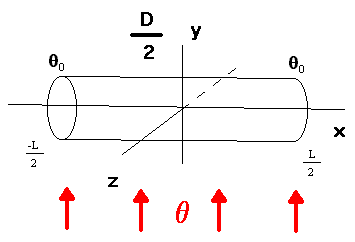
Узкий цилиндрический стержень помещён в термический поток с неизменной температурой , на концах стержня поддерживается неизменная температура 0
.
1.2 Математическая модель
Совместим координатную ось абсцисс с продольной осью стержня с началом посреди стержня. Будем разглядывать задачку (распределения температуры по стержню) мосле момента установления режима Т0
.
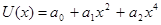
1-ая математическая модель употребляет экспериментальные данные, при всем этом определяют температуру Ui
стержня в нескольких точках стержня с координатами xi
. Результаты измерения Ui
разглядывают как функцию регрессии и получают статистики. Беря во внимание чётность U(x) можно находить её в виде многочлена по чётным степеням x (ограничимся 4-ой степенью этого многочлена).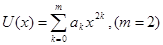
(1.1)
задачка сводится к отысканию оценок неведомых характеристик, т.е. коэффициентов a0
, a1
и a2
, к примеру, способом меньших квадратов.
2-ая математическая модель, также использующая экспериментальные данные, состоит в применении интерполяционных формул и может употребляться, если погрешность измерений температуры Ui пренебрежимо мала, т.е. можно считать, что U(xi
)=Ui
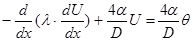
3-я математическая модель базирована на использовании закона теплофизики. Можно обосновать, что разыскиваемая функция U(x) имеет вид:
(1.2)
где коэффициент теплопроводимости, коэффициент теплоотдачи, D – поперечник стержня, температура потока, в который помещён стержень.
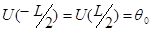
Отыскиваем U(x) как решение краевой задачки для уравнения (1.2) с граничными критериями:
(1.3)
на отрезке [-L|/2;L/2], где L – длина стержня,
неизменная температура, поддерживаемая на концах стержня.
Коэффициент теплопроводимости зависит от температуры:
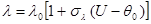
(1.4)
где
изначальное значение коэффициента теплопроводимости,
вспомогательный коэффициент.
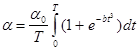
Коэффициент теплоотдачи вычисляют по формуле:
(1.5)
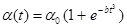
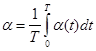
т.е. как среднее за некий отрезок времени от 0 до Т, тут
значение при t стремящемся к бесконечности, b – узнаваемый коэффициент.
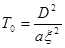
время Т0
, по истечении которого распределение температуры в стержне можно считать установившимся определяется по формуле:
(1.6)
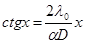
где а – коэффициент температуропроводности, меньший положительный корень уравнения:
(1.7)
Задание курсовой работы
Вариант № 136
Начальные данные:
L = 0.0386 м
D = 0,00386 м
о
С
о
С
141,85 (Вт/м*К)
2,703*10-4
6,789*10-7
3,383*102 (Вт/м2
*К)
218 о
С
А = 3,043*10-5 (м2
/с)
11
X, м
U, o
C
0
353
0,00386
343
0,00772
313
0,01158
261
0,01544
184
0,01930
74
2. Обработка результатов опыта.
2.1 задачка регрессии. Способ меньших квадратов.
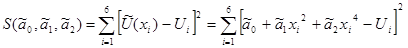
Отыскиваем функцию регрессии в виде (1.1). Оценки коэффициентов находим при помощи МНК, при всем этом меньшими будут оценки, обеспечивающие минимум квадратов отклонений оценочной функции регрессии от экспериментальных значений температуры; суммирование ведут по всем экспериментальным точкам, т.е. минимум величины S:
(2.1)
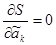
В нашем случае нужным т достаточным условием минимума S будут:
Где k = 0, 1, 2. (2,2)
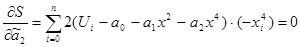
Из уравнений (2.1) и (2.2) получаем: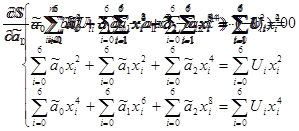
(2.3)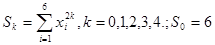
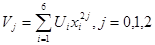
Сумма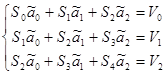
Система (2.3) воспримет вид:
(2.4)
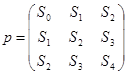
В итоге вычислений получаем Sk
и Vj
. Обозначим матрицу коэффициентов уравнения (2.4) через “p”: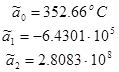
Способом Гаусса решаем систему (2.4) и найдём оборотную матрицу p-1
. В итоге получаем: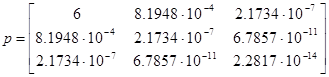
Подставляя в (2.1) отысканные значения оценок коэффициентов ак
, находим малое Smin
=0.7597
При построении доверительных интервалов для оценок коэффициентов определяем за ранее точечные оценки.
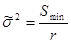
Предполагается, что экспериментальные значения xi
измерены с пренебрежимо малыми ошибками, а случайные ошибки измерения величины Ui
независимы и распределены по нормальному закону с неизменной дисперсией
, которая неведома. Для имеющихся измерений температуры Ui
неведомая дисперсия оценивается по формуле: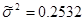
Где r – число степеней свободы системы, равное разности меж количеством экспериментальных точек и количеством вычисляемых оценок коэффициентов, т.е. r = 3.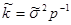
Оценка корреляционной матрицы имеет вид: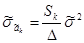
Оценки дисперсий характеристик оценок коэффициентов найдём по формулам:
Где Sk
– минор соответственного диагонального элемента матрицы обычной системы;
основной определитель обычной системы.
В нашем случае:
S0
=3.5438 10-22
S1
=-8.9667 10-14
S2
=6.3247 10-7
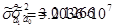
Откуда: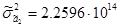
Отысканные оценки коэффициентов распределены по нормальному закону, т.к. линейно зависят от линейно распределённых экспериментальных данных Ui.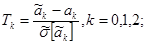
Понятно, что эти оценки несмещённые и действенные. Тогда случайные величины:
Имеют распределения Стьюдента, а r = 3.
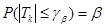
Избираем доверительную возможность =0,9 и по таблице Стьюдента находим критичное
Доверительные интервалы для коэффициентов:
(2.4*)
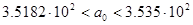
В нашем случае воспримут вид: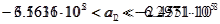
2.2 Проверка статистической догадки о адекватности модели задачки регрессии.
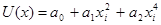
Имеется подборка объёма n экспериментальных значений (xi
;Ui
). Предполагаем, что ошибки измерения xi
пренебрежимо малы, а случайные ошибки измерения температур Ui
подчинены нормальному закону с неизменной дисперсией
Мы избрали функцию регрессии в виде:
Выясним, недозволено ли было ограничиться многочленом второго порядка, т.е. функцией вида:
(2.5)
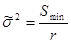
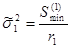
C помощью МНК можно отыскать оценки этих функций и несмещённый оценки дисперсии отдельного измерения Ui для этих случаев:
Где r1
= 4 (количество точек – 6, параметра – 2).
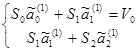
Обычная система уравнений для определения новейших оценок коэффициентов функции (2.5)при помощи МНК имеет вид:
(2.7)
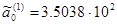
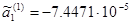
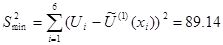
Решая эту систему способом Гаусса, получим:
(2.8)
Чем лучше функция регрессии обрисовывает опыт, тем меньше для неё обязана быть оценка дисперсии отдельного измерения Ui, т.к. при нехорошем выборе функции в дисперсию войдут связанные с сиим выбором доп погрешности. Потому для того, чтоб создать выбор меж функциями U(x) и U(1)(x) необходимо проверить значимость различия меж надлежащими оценками дисперсии, т.е. проверить догадку:
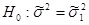
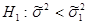
Н0 – другая догадка
Т.е. проверить, значимо ли уменьшение дисперсии при увеличении степени многочлена.
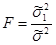
В качестве статического аспекта разглядим случайную величину, равную:
(2.9)
имеющую распределение Фишера с(r ; r1
) степенями свободы. Избираем уровень распределения Фишера, находим критичное
В нашем случае F=349.02, а F*
=10,13.
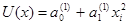
Если б выполнилось фактически неосуществимое соотношение F>F
, имевшее возможность 0,01, то догадку Н0
пришлось бы отклонить. Но в нашем случае можно ограничиться многочленом
, коэффициенты в каком неодинаковы.
3. Нахождение коэффициента теплопроводимости .
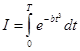
Коэффициент вычислим по формуле (1.5), обозначим: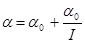
(3.1)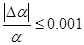
Определим допустимую абсолютную погрешность величины интеграла I, исходя из требования, чтоб относительная погрешность вычисления не превосходила 0,1%, т.е.:
(3.2)
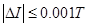
Т.к. из (3.1) разумеется, что
, то условие (3.2) заранее будет выполнено, если:
(3.3)
Т.е. в качестве максимально допустимой абсолютной погрешности вычисления интеграла I возьмём 0,001Т (3.4)
Т=218 о
С, как следует, 0,218 о
С.
3.1 Вычисление интеграла
I
способом трапеции
Внедрение теоретической оценки погрешности
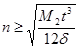
Для обозначения требуемой точности количества частей n, на которые необходимо разбить отрезок интегрирования [0;T] определяется по формуле:
, где M
[f”(t)], te [0;T], f(t)=e-
bt
3
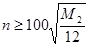
Беря во внимание формулу (3.4) получаем:
(3.5)
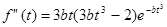
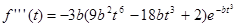
Дифференцируя f(t), получим: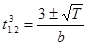
А нужное условие экстремума: f”(t)-f’’’(t)=0, откуда получаем:
Дальше вычисляем значения f’’(t) при t=t1
, t=t2
, t=0 и t=T, получаем:
f’’(t1)=1.5886 10-4
f’’(t2)=-1.6627 10-4
f’’(0)=0
f’’(T)=7.4782 10-6
Итак: M
1,5886 10-4
, откуда n=25.66; принимаем N=26.

Дальше вычислим интеграл I:
Погрешность вычисления :

3.2 Вычисление интеграла I способом парабол


При расчётах будем применять теоретическую оценку погрешности при помощи правила Рунге. Для обеспечения данной точности количество частей n, на которое следует поделить интервал интегрирования можно найти по формуле:
, откуда:
Нахождение М4
можно провести аналогично нахождению М2
в прошлом пт, но выражение для fIV
(t) имеет достаточно массивный вид. Потому правило Рунге – более обычный метод.
Обозначим через In
и I2
n

Будем , начиная с n=2, умножать n до того времени, пока не начнёт производиться неравенство (*1), тогда:
(3.6)

Согласно формуле парабол (3.7):
Результаты вычислений сведём в таблицу:
n
In
I2n
4
102.11
8
101.61
0.5017
По формуле (3.7) I = 101,61 что в границах погрешности совпадает со значением, приобретенным по способу трапеций
n=8
n=4
ti
(8)
y8
ti
(4)
y4
0
1
0
1
27.25
0.9864
54.5
0.8959
54.5
0.8959
81.75
0.6901
109
0.4151
109
0.4151
136.25
0.1796
163.5
0.0514
163.5
0.0514
190.75
0.0089874
218
0.00088179
218
0.00088179
4. Вычисление времени Т0
установления режима
4.1 Решение уравнения комбинированным способом
время установления режима определяется по формулам (1.6) и (1.7).
Проведём поначалу отделение корней. Имеем y = ctg(x) и y = Ax. Приведём уравнение к виду: Axsin(x)-cos(x) = 0. Проведём процесс отделения корня.
F(x)
-1
-0.6285
0.4843
x
0.01
0.05
0.1
т.е. с [0.01;0.05]
Убедимся, что корень вправду существует и является единственным на избранном интервале изоляции.
f(a) f(b)<0 – условие существования корня производится
f’(x) на [a;b] – знакопостоянна: f’(x)>0 – условие единственности также производится. Проведём уточнение с погрешностью не превосходящей
Строим касательные с того конца, где f(x) f”(x)>0

f”(x)=(2A+1)cos(x) – Axsin(x). f”(x)>0 на (a;b), как следует касательные строим справа, а хорды слева. Приближение корня по способу касательных: 
по способу хорд:
Вычисление ведём до того момента, пока не выполнится условие:
Результаты вычислений заносим в таблицу:
n
an
bn
f(an
)
f(bn
)
0
0.05
0.1
-0.6285
0.4843
1
0.07824
0.08366
-0.0908
0.0394
2
0.08202
0.08207
-9.1515 10-4
3.7121 10-4
3
0.08206
0.08206
-8.4666 10-8
3.4321 10-8
Т0
= 72,7176 секунд.
4.2 Решение уравнения комбинированным способом
Приведём f(x) = 0 к виду x = (x). Для этого умножим обе части на случайное число , неравное нулю, и добавим к обеим частям х:
X = x — f(x)

xx — Axsin(x) + cosx)
В качестве возьмём:
где М = max [f’(x)] на [a;b], а m = min [f’(x)] на [a’b]
В силу монотонности f’(x) на [a;b] имеем m = f’(а), М = f’(b). Тогда 0,045.


Приближение к корню отыскиваем по последующей схеме:

Вычисление ведём до того времени, пока не выполнится условие:
(q = max |’(x)| на [a’b])
’(x) на [a’b] однообразно убывает, потому максимум его модуля достигается на одном из концов.
’(0,05) = 0,3322 ’(0,1) = -0,3322, как следует, q = 0.3322 < 1. В этом случае производится условие сходимости и выходит последовательность:
i
xi
( xi
)
xi
0
0.075
0.082392
0.00739
1
0.082392
0.082025
0.000367
2
0.082025
0.08206
3.54 10-5
3
0.08206
0.082057
3.33 10-6
4
0.082057
0.082057
3.15 10-7
Итак, с погрешностью, наименьшей 10-4
, имеем:
Т0 = 72,7176 с. , 0.03142
5. Решение краевой задачки

Используем способ малого параметра. Краевую задачку запишем в виде:
(5.1)


Введя новейшую переменную y = (U —
, запишем (5.1) в виде:
(5.2)

0.18L/2 =0.0193. В качестве малого параметра возьмём .

Тогда, подставив y(x) в уравнение (5.2) и перегруппировав члены при схожих степенях , получим:
(5.3)

Ограничимся 2-мя первыми членами ряда:
Из (5.2) и (5.3) находим общее решение уравнения для y0
:
где y0
с тильдой – личное решение данного неоднородного уравнения; y(1)
и y(2)
– линейно независящие решения однородного уравнения.


Корешки уравнения:
y0общ
= 1 + c1
ch(px)+c2
sh(px), где p = 0.01953

Константы найдём из граничных критерий:
откуда с1
= 0, с2
= -0,57; т.е. имеем функцию:
y0
= 1 — 0.57 sh(px)

Общее решение:
Личное решение:
Дифференцируя и подставляя в уравнение, получим:
А1
= 0; А2
= -0,1083; В1
= 0; В2
= 17,1569;
Тогда общее решение для y1
имеет вид:

с3
= 0; с4
= 0,0462
Перейдя к старенькой переменной U, получим:



Итоговое уравнение:
Пользуясь данной формулой, составим таблицу значений функции U(x):
x
U(x)
U
0
352.9075
353
0.0019
350.4901
0.0039
343.1972
343
0.0058
330.9053
0.0077
313.4042
313
0.0097
290.391
0.0116
261.4598
261
0.0135
226.0893
0.0154
1836255
184
0.0174
133.2579
0.0193
74
74
Используя данную таблицу, строим график функции U(x).
[см. приложение 1]
6. Заключение
Решение задачки на ЭВМ с помощью вычислительной системы ManhCad 7.0 отдало результаты (функцию распределения температуры в узком цилиндрическом стержне), приобретенные по решению практического задания и обработкой опыта (функции регрессии), которые фактически (в границах погрешности) совпадают с экспериментальными значениями.
Перечень литературы
1. Методические указания «Способы приближённых вычислений. Решение нелинейных уравнений» (ЛТИ им. Ленсовета, Л. 1983)
2.Методические указания «Приближённые способы ислисления определённых интегралов» (ЛТИ им. Ленсовета, Л. 1986)
Методические указания «Исследование распределения температуры в узком цилиндрическом стержне» (ЛТИ им. Ленсовета, Л. 1988)
]]>

