Учебная работа. Реферат: Компьютерные технологии решения оптимизационных задач управления

Учебная работа. Реферат: Компьютерные технологии решения оптимизационных задач управления

Содержание

1. Компьютерные технологии решения оптимизационных

задач управления 3

2. Обзор задач способов и пакетов приложений встроенных математических сред 7

3. понятие о численных способах лежащих в базе компьютерной реализации процесса принятия оптимизационных решений 15

4. Идеи способов одномерной оптимизации 18

Перечень использованной литературы 26

1. Компьютерные технологии решения оптимизационных задач управления

Оптимизация — целенаправленная деятельность, заключающаяся в получении лучших результатов при соответственных критериях. задачки оптимизации — это задачки нахождения наибольшего либо малого значения некой функции, именуемой мотивированной функцией. Если заданы ограничения на аргументы данной функции, то задачка именуется задачей условной оптимизации, если ограничения не накладываются, то задачей бесспорной оптимизации.

Огромное распространение получили задачки линейного программирования- задачки, в каких линейны как мотивированная функция, так и ограниченная в виде равенств либо неравенств. Линейное программирование тесновато соединено с иными способами математического программирования. На практике нередко приходится встречаться со вариантами, когда целью оптимизации является установление лучшей последовательности те6х либо других работ, такие задачки именуют задачки динамического программирования. В остальных задачках оптимизации, в качестве переменных выступают функции — вариационные задачки. Есть задачки оптимизации с несколькими мотивированными функциями — задачки системной оптимизации.

Для решения задач данного типа используются такие способы как:

1) Симплекс-метод,разработанный Danzig’oM около 50 лет вспять, перебирает «базовые» решения, построенные методом фиксирования доста­четкого количества переменных, чтоб матрица системы ограничений Ах = b стала квадратной. Таковая приобретенная система быть может решена для единственных значений оставшихся переменных. Базовые решения являются экстремальными граничными точками области допустимых решений, опреде­ляемой системой ограничений, и симплекс-способ может рассматриваться как прохождение от одной таковой точки к иной по границе области.

2) Способ барьеров либо внутренних точек,с иной стороны, обхо­дит точки из внутренней части области допустимых значений. Эта группа
способов происходит от технологий нелинейного программирования, разработанных и популяризованных в 60-х гг. Fiacco и McCormick, но их приложения к линейному программированию датируются лишь 1984 г.

3) Схожая ЛП задачка целочисленного программирования(либо
целочисленного линейного программирования, поточнее говоря) допускает
лишь целочисленные значения переменных. Задачки ЦП обычно поближе к ре­альным задачкам, чем задачки ЛП, но намного наиболее трудоемки в решении.
Более обширно применяемые способы решения задач ЦП употребляют решение серии задач ЛП, чтоб отыскать целочисленные решения и обосновать оп­тимальность. Потому большая часть ПО ЦП построена на базе ПО ЛП, и данный FAQ применим для решения задач этих 2-ух видов.

Линейное и целочисленное программирование годно для модели­рования огромного количества разных заморочек в планировании, маршрутизации, разработке расписаний, назначениях и дизайне. ЛП и его расширения ис­пользуются в транспортной промышленности, энергетике и машиностроении.

В жизни решение задач оптимизации занимает весьма много времени и это довольно трудозатратный процесс, где нужно учитывать все характеристики. И чтоб облегчить нам работу по поиску оптимума программеры различных государств написали огромное количество программ для решения задач оптимизации фактически во всех отраслях производства и сферах нашей жизни.

Система Mathematica соединяет воединыжды внутри себя припас глобальных математических познаний, скопленных в справочной литературе, и употребляет свои собственные
революционные методы, чтоб развивать эти познания.

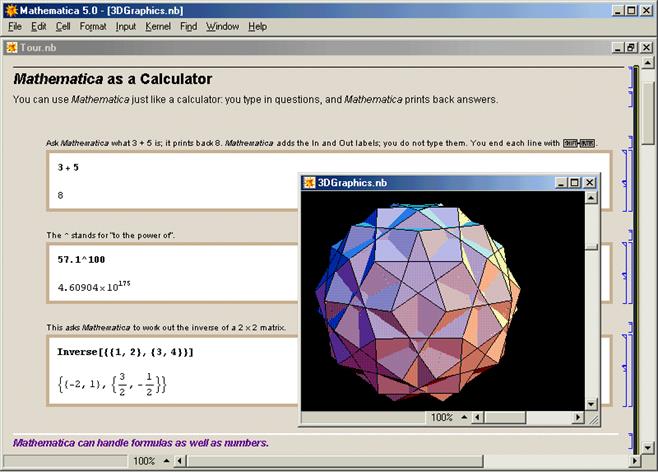
Рис.1 – интерфейс программки Mathematica

Умение проводить аналитические расчеты — одно из основных плюсов данной программки, автоматизирующей математические расчеты. Mathematica умеет преобразо­вывать и упрощать алгебраические выражения, диффе­ренцировать и вычислять определенные и неопределен­ные интегралы, вычислять конечные и нескончаемые сум­мы и произведения, решать алгебраические и дифферен­циальные уравнения и системы, также разлагать функ­ции в ряды и отыскивать пределы

Int=Integrate [a*x^5/Sqrt[x^3-1], x]

В почти всех видах вычислений система Mathematica является мировым рекордсменом по скорости.

Mathematica дозволяет строить 2-ух и трехмерные графики разных типов в виде точек и полосы на плоскости, поверхностей, также контурные, градиентные (dencityplot), параметрические. Mathematica делает построение графика в три эта­па. На первом создается огромное количество графических прими­тивов, на втором они преобразуются в независящее от вы­числительной платформы описание на языке PostScript, а на 3-ем это описание переводится в графический фор­мат для той системы, на которой установлена Mathematica.

Рис.2 – 3D-график

Иная сторона развития программного обеспечения — ориентация на “непрограммирующего юзера”. В этом случае юзер такового пакета получает возможность сосредоточиться на сути самой задачки, а не методах ее программной реализации. В свою очередь юзер должен ясно представлять способности применяемого пакета и заложенных в нем способов, также уметь избрать нужный пакет, соответственный решаемой задачке.

Все этапы сотворения и использования математической модели просто проследить при работе с пакетом MATHCAD конторы “MathSoft Inc.” (USA).

2. Обзор задач способов и пакетов приложений встроенных математических сред

Современные пакеты обработки печатной продукции включают средства дизайна текста, подготовки математических формул, графиков, схем, таблиц. Современные информационные технологии разрешают приготовить документ, который может включать как объекты документы остальных типов либо гиперссылки на остальные документы и программки обработки.

Индивидуальные компы получили наибольшее применение (по количеству) в задачках моделирования. Их вначале обширное внедрение определялось, до этого всего, не их быстродействием, а возможностью гармонически настроить рабочее пространство исследователя, организовать передачу данных меж задачками, получить отлично оформленный отчет.

В конце концов, современное развитие информационных технологий, нацеленных на создание встроенных пакетов мультимедиа-технологии, привело к возникновению компьютерных математических систем, к которым относятся Maple V конторы Waterloo Maple Software Inc.

системы компьютерной алгебры (СКА) весьма многочисленны, но не наиболее 10 из их являются по-настоящему современными, общими и довольно распространёнными. СКА различаются друг от друга количеством интегрированных функций; в неких системах их имеется несколько 10-ов, в остальных – на порядок больше. Внутренние структуры этих систем значительно различаются одна от иной. Тем не наименее, большая часть СКА владеют последующими общими качествами:

— они все имеют набор так именуемых интегрированных функций (базовых предпрограммируемых установок), которые предусмотрены для вычислений (численных, символьных, графических);

— работа юзера со встроенными функциями происходит в интерактивном режиме; юзер имеет возможность вмешиваться в ход вычислений в хоть какой момент;

— входные данные представляют собой выражения, у каких, по наименьшей мере, начальное язык юзера – совокупа интегрированных функций и их опций, а в неких СКА, к тому же, предоставляют возможность определения процедур при помощи операторов традиционных языков программирования (If, While и др.);

— СКА являются открытыми для юзера системами, по другому говоря, юзер может создавать новейшие функции на базе интегрированных функций.

— вычислительное ядро имеет структуру перечня либо дерева, а управление памятью — динамическое, с автоматическим восстановлением доступного места;

— язык реализации системы укрыт от юзера (содержится в так именуемом вычислительном ядре системы); это почаще всего С либо Lisp (время от времени Pascal);

Компьютерные математические системы дают юзеру возможность применять интегрированный язык программирования сверхвысокого уровня, позволяющий расширять класс задач, охваченных встроенными функциями, и решать такие задачки, которые нереально решить в рамках использования интегрированных функций.

Дальше мы разглядим программное обеспечение индивидуальных компов, применяемое на разных шагах математического моделирования.

За крайние годы чётко сформировалась последующая тенденция в развитии программного обеспечения для индивидуальных ЭВМ : возникает всё больше встроенных пакетов, которые включают наряду со спец программками и программки подготовки отчетов. Модульный подход к моделированию выслеживается и в современных пакетах.

Одним их из их является MatLab (“The MathWorks Inc”, USA), который, по существу, вначале предназначался для “огромных” машин, а потом был приспособлен для индивидуальных компов.

Система MatLab

Данная система нацелена на матричные и векторные вычисления (её заглавием является сокращение словосочетания Matrix Laboratory) и предназначена в главном для численного моделирования технических систем. Её крайние версии содержат элементы всепригодных систем компьютерной алгебры: особый модуль MatLab Notebook, позволяющий, в том числе, ис­пользовать способности Microsoft Word для дизайна документов, также приобретённый у компании Maple Waterloo модуль главный символьной библиотеки системы Maple V 4.0 для выполнения неких аналитических расчётов. Входной язык в определённой мере припоминает BASIC (с элементами Фортрана и Паскаля). интерфейс наименее доступный и яркий, чем у системы MathCAD, но скорость вычислений выше.

Внедрение в образовании нецелесообразно; система создана для проф работы в области арифметики и смежных областях.

Система MatLab создана для выполнения инженерных и научных расчетов и качественной визуализации получаемых результатов. Эта система применяется в арифметике, вычислительном опыте, имитационном моделировании.

В пакет заходит огромное количество отлично испытанных численных способов (решателей), операторы графического представления результатов, средства сотворения диалогов. Отличительной индивидуальностью MatLab по сопоставлению с обыкновенными языками программирования является матричное язык MatLab дает возможность инженерам и ученым просто реализовывать свои идеи. Массивные численные способы и графические способности разрешают инспектировать догадки и новейшие возникающие идеи, а встроенная среда дает возможность стремительно получать практические результаты.

сейчас MatLab употребляется во огромном количестве областей, посреди которых обработка сигналов и изображений, проектирование систем управления, денежные расчеты и мед исследования. Его открытая архитектура делает вероятным внедрение MatLab и сопутствующих товаров для исследования данных и сотворения собственных инструментов, использующих многофункциональные способности MatLab.

Иная сторона развития программного обеспечения – ориентация на наименее мастерски приготовленного, “непрограммирующего юзера”. В этом случае юзер такового пакета получает возможность сосредоточиться на сути самой задачки, а не методах ее программной реализации. Но, в свою очередь, юзер должен ясно представлять способности применяемого пакета и заложенных в нем способов, также уметь избрать нужный пакет, соответственный решаемой задачке. Все этапы сотворения и использования математической модели просто проследить при работе с пользующимся популярностью пакетом MathCAD (Компания“MathSoft Inc.”, USA).

MATHCAD — всепригодный математический пакет, созданный для выполнения инженерных и научных расчетов. Математическое обеспечение пакета дозволяет решать почти все задачки в объеме инженерного университета.

Создатели пакета улучшают пакет от версии к версии. В истинное время существет версия MATHCAD 13, владеющая еще большенными способностями. Есть уникальная (английская) и русифицированная версии программки.

Что различает пакет MATHCAD от калькулятора: вычисление с случайной точностью, работа с разными типами данных (всеохватывающие, векторы, матрицы), внедрение библиотеки математических функций (которая быть может дополнена программками на ФОРТРАНе).

Основное преимущество пакета перед обычными языками программирования — естественный математический язык, на котором формулируется решаемая задачка.

Пакет соединяет воединыжды внутри себя: редактор математических формул, интерпретатор для вычислений, библиотеку математических функций, машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) (либо вычислительной системы) которое делает арифметические и логические операции данные программкой преобразования инфы управляет вычислительным действием и коор символьных преобразований, текстовый редактор, графические средства представления результатов. Пакет MATHCAD относится к встроенным пакетам, т.е. дозволяет не только лишь произвести вычисления, да и получить документ — итоговый отчет с комментами, формулами, таблицами и графиками. В отличие от издательских систем формулы в MATHCAD работают.

К положительным качествам MATHCAD следует отнести открытость — все приведенное в документе быть может воспроизведено, а Интеграция в одном документе начальных данных, способа решения и результатов дозволяет сохранить опции для решения схожих задач.

Рис. 3 – интерфейс программки Mathcad

Рис. 4 – Интерфейс программки Microsoft Excel

программка MS Excel является фаворитом на рынке программ обработки электрических таблиц, описывает тенденции развития в данной области.

Одним из важных многофункциональных расширений программки, созданным для экспертов, является интегрированная в Excel Среда программирования Visual Basic (VBA) для решения прикладных задач.

Главные способности программки MS Excel:

1. Управление файлами

2. Построение таблиц

3. Табличные вычисления

4. Построение и оформление диаграмм

5. Вставка наиболее 200 функций

6. Обмен данными

7. Обработка списков

8. анализ данных

9. Конфигурирование программки MS Excel

10. Интегрированный язык VBA

11. Решение задач оптимизации с исполь­зованием надстройки Поиск решения

Система REDUCE
Данная система хронологически сумеет считаться одной из наистарейших систем компьютерной алгебры, её 1-ая версия возникла в 1969 г. Входной язык по задачки требуется составить программку, которая состоит из серии установок, представляющих из себя вызовы функций, условные операторы, циклы и т. п. Система при переходе к любому последующему шагу интерпретирует команду в порядке поступления и делает её.
Система REDUCE рассчитана на проф внедрение при сложных вычислениях, имеет огромную библиотеку функций и реализуется на “огромных” ЭВМ , что делает её применение в образовании фактически неосуществимым.
Система Macsyma.
Система Macsyma, как и REDUCE, структурирована по эталону высокоуровневых языков программирования. Её новенькая версия (Macsyma 2.3) владеет рядом увлекательных особенностей, к которым можно отнести применение самых современных алгоритмов численных расчётов библиотек, таковых как LINPACK и EISPACK, благодаря интегрированным в систему командам программки MatLab. Не считая того, имеется интегрированная электрическая таблица для обработки данных и особое массивное, взаимосвязанное с интерфейсом Macsyma, дополнение, созданное для решения дифференциальных уравнений с личными производными способом конечных частей. Как и REDUCE, данная система рассчитана на внедрение математиками-профессионалами.
Система Derive
Система Derive, на взор почти всех юзеров, весьма органично соединяет способности проведения численных и символьных вычислений с простотой в воззвании и низкими требованиями к применяемой компьютерной технике. Крайнее событие является в особенности значимым аргументом в пользу внедрения данной системы в образовании. Derive имеет многооконный интерфейс юзера и комфортную систему меню. Языком реализации является “Lisp” — один из самых узнаваемых многофункциональных языков, направленный на решение задач искусственного ума и построение экспертных систем. Ввод математических знаков производится с клавиатуры набором слов, которые порождают на мониторе изображения соответственных математических знаков, по мере необходимости — в двумерном виде (как, к примеру, простые дроби). Интегрированный графический редактор дозволяет получать двумерные графики в декартовых и полярных системах координат и трёхмер­ные графики, с возможностью автоматического масштабирования.
Значимым достоинством современных версий Derive будет то, что они относятся к расширяемым системам, способным приспособиться к решению определенных задач, формулируемых данным юзером.
Но недочетом системы Derive является ограниченная возможность для программирования юзером. Внедрение системы Derive в образовании может быть, и это сейчас уже реализуется в неких университетах и даже школах.

3.понятие о численных способах лежащих в базе компьютерной реализации процесса принятия оптимизационных решений

Обилие нелинейных задач математического программирования (с полной либо неполной информацией) вызывает необходимость разработки способов оптимизации, не связанных конкретно с анализом критерий существования X* и полностью базирующихся на вычислительных и логических операциях.

Идеи этих способов обычно ординарны; как правило, они следуют из эвристических суждений, сводя делему решения задачки к построению соответствующего метода поиска X*, г*, при этом желаемые характеристики таковых алгоритмов оговариваются заблаговременно.

Численные способы играют значительную роль в решении принципиальных для практики оптимизационных решений.

В отдельных вариантах бывает тяжело найти, к какому классу относится та либо другая задачка и существует ли для нее обоснованный способ решения.

На выбор способа может влиять рвение очень применять мощности ЭВМ с целью понижения издержек на исследования (если схожая перспектива реальна).

Обозначенные происшествия разрешают разглядывать численные способы оптимизации как нужное средство решения заморочек поиска оптимума в исследовательских работах, разных по содержанию и трудности.

Рассмотренные положения разрешают доказать приемлемость тех либо других численных способов для решения экстремальных задач.

Вычисление определенных интегралов.

Разглядим пример: .

Сначала нужно сделать функцию,вычисляющую подынтегральное выражение.

Для вычисления интеграла вызовем функцию quad, задав первым аргументом ссылку на функцию fint, а вторым и третьим — нижний и верхний пределы интегрирования.

По дефлоту функция quad вычисляет приближенное аргумент:

Вычисление двойных интегралов.

В MATLAB определена функция dblquad для приближенного вычисления двойных интегралов. Как и в случае вычисления определенных интегралов, следует написать файл-функцию для вычисления подынтегрального выражения. Вычислим интеграл:

Как следует, функция обязана содержать два аргумента x и y:

Функция dblquad имеет 5 входных аргументов. При ее вызове нужно учитывать, что первыми задаются пределы внутреннего интеграла по х, а вторыми — наружного по у:

Интегралы, зависящие от параметра.

Функции quad и quadl разрешают отыскивать значения интегралов, зависящих от характеристик. Аргументами функции, вычисляющей подынтегральное выражение, обязана быть не только лишь переменная интегрирования, да и все характеристики. значения характеристик указываются через запятую, начиная с шестого аргумента quad либо quadl.

Решим интеграл:

Зададим функцию

Используя quad, вычислим интеграл:

4.Идеи способов одномерной оптимизации

Численные способы оптимизации классифицируются последующим образом.

1. По размерности решаемых задач: одномерные; многомерные.

Одномерная оптимизация: Способ сканирования. Способ деления напополам. способ золотого сечения. Способ параболической аппроксимации.

Многомерная бесспорная градиентная оптимизация: Способ градиента. Способ наискорейшего спуска. способ сопряженных градиентов. Способ томного шарика.

Многомерная безградиентная оптимизация: Способ Гаусса-Зайделя (покоординатный спуск). способ Розенброка. Симплексный способ (способ дифференцируемого полиэдра). способ параллельных касательных.

Многомерная случайная оптимизация: способ слепого поиска. Способ случайного направления. способ поиска с «наказанной случайностью». Способ с «блуждающим» поиском.

Многомерная условная оптимизация: Способ штрафов. Способ прямого поиска с возвратом. способ проектирования градиента.

Постановка: требуется улучшить х (формальная постановка)

— функция одной переменной

— мотивированная функция.

Решение: отыскать х, при котором воспринимает среднее

2 варианта:

— минимизировать – задачка минимизации;

— максимизировать – задачка максимизации.

Разглядим вариант минимизации

2 метода:

— аналитический

— численный

В аналитическом задается в виде формулы, в численном задается в виде темного ящика, на входе подается х, на выходе

Пусть функция определена в некой области
(), в случае одномерной оптимизации S – интервал :

1. точка именуется глобальным минимумом, если для

2. точка именуется серьезным глобальным минимумом, если для

3. точка именуется локальным минимумом, если для

4. точка именуется серьезным локальным минимумом, если для

Следствие: неважно какая точка глобального минимума является локальным минимумом, оборотное не правильно.

Аналитический метод нахождения локального минимума.

— дифференцируема

— нужное условие точки локального минимума.

Численные способы

Пусть функция задана на интервале , при всем этом существует таковая точка , что на – однообразно убывает, а на – однообразно растет, то функция унимодальная.

Если из того что следует, что , то функция именуется однообразно растущей. Если из того что следует, что , то функция именуется однообразно убывающей.

способы одномерного поиска

Разобьем и вычислим

В итоге остается интервал наименьшего размера, к которому применяется этот же способ, и находим очередной интервал, в конце находим интервал с заранее подходящей точкой.

Интервал неопределенности – интервал, в каком заранее находится точка минимума. Более действенное разбиение – 2-мя точками на 3 равных отрезка.

1)

2)

— опосля выполнения n шагов сокращение начального интервала

— точность с которой нужно отыскать решение задачки.

N=2n, где n – число шагов, N – число вычислений (мера эффективности данного решения).

способ золотого сечения

Точки должны быть размещены на равном расстоянии.

; ; ;

; — золотое сечение.

— величина сокращения на любом шаге

число итераций вырастает как логарифм функции.

Одномерная оптимизация с внедрением производных

. Пусть мотивированная функция дифференцируема .

точка локального минимума
точка локального максимума

способы для нахождения корня уравнения функции 1-ой производной от начальной

Нахождение локального минимума либо максимума сводится к нахождению корней первой производной от данной

Если
представляет собой многочлен, то уравнение именуется
(полиномиальным), если
представлена тригонометрическими, логарифмическими, показательными и т.п. функциями, то уравнение именуется
.( вдальнйшем заместо

будем употреблять

)

Решение уравнения вида разбивается на два шага:

1. отделение корней, т.е. отыскание довольно малых областей, в каждой из которых заключен один и лишь один корень уравнения;

2. вычисление выделенного корня с данной точностью.

На первом шаге может посодействовать построение приближенного графика функции
либо, если функция довольно непростая, то можно попробовать представить уравнение в виде и выстроить два графика и , тогда корнями уравнения будут абсциссы точек пересечения этих кривых.

Выбор интервалов, в каких имеется один и лишь один корень делается на основании узнаваемых параметров непрерывных функций:

—

—

—

Для вычисления выделенного корня существует огромное количество приближенных способов. Они все вычисляют , т.е. данное количество цифр опосля запятой. Разглядим последующие способы:

— половинного деления;

Способ половинного деления

Сущность способа половинного деления (дихотомии) заключается в последующем.

Отрезок
делится напополам и за 1-ое приближение корня принимается точка
, которая является серединой отрезка, т.е.. Если , это корень уравнения. Если нет, то дальше выбирается тот из отрезков [
,
] либо [
,
], на концах которого функция имеет различные знаки. Приобретенный отрезок опять делится напополам, и проводятся те же рассуждения. Деление длится до того времени, пока длина отрезка не станет меньше данного .

способ половинного деления реализуется в виде последующего метода:

Отыскать точку
= (
+
)/2.

Если
(
)×
(
) <0, то корень лежит на интервале [
,
], если нет, то корень лежит на интервале [
,
].

Если величина интервала не превосходит некое довольно маленькое число
, то найден корень с точностью
, по другому возврат к п.1.

Невзирая на простоту, этот способ просит очень огромного количества вычислений и не постоянно дозволяет отыскать решение с
точностью.

Блок-схема метод решения уравнения способом деления напополам.

Перечень использованной литературы

1. Автоматизация вычислений и компьютерное моделирование. MS Excel и MathCad : учебное пособие / Н.В. Вознесенская. – Саранск : Изд-во Мордовского института, 2004. – 91 с.

2. Дьяконов, В. MathCad 2001: особый справочник / В. Дьяконов. – СПб. : Питер, 2002. – 832 с.

3. Информатика : учебник / Макарова Н. В. [и др.]. – М. : деньги и статистика, 1997. —768с.

4. исследование операций в экономике: Учебное пособие для вузов / Кремер Н.Ш. [и др.]. – М.: ЮНИТИ, 2002. – 407 с.

5.Кудрявцев, Е. Н. Исследования операций в задачках, методах и программках / Е.Н. Кудрявцев. М., Наука, 1982. – 150 с.

6.Кузнецов, Ю. Н. Математическое программирование / Ю.Н. Кузнецов, В.И. Кузубов, А.В. Волощеноко. — М.: Высшая школа, 1980. – 320 с.

7. Леонтьев, Ю. Microsoft Office 2000. Лаконичный курс / Ю. Леонтьев. – СПб.: Питер, 2001. – 760 с.

8.Сидоров, М. Е. Решение задач рационального планирования в таблицах Excel // Информатика и образование. – М., 2001. – № 1. – с. 36 – 51.

9.Эталон компании. Общие требования и правила дизайна курсовых и дипломных работ и объяснительных записок к курсовым и дипломным проектам.

10.Ширяев, В.Д. Экономико-математические способы: учебное пособие / В.Д. Ширяев, Н.М. Куляшова. – Саранск : Изд-во Мордовского института, 2002. – 112 с.

11.Финансовая информатика: Учебник / Косарев В.П.. – М.: деньги и статистика, 2004. – 592 с.

]]>