Учебная работа. Курсовая работа: Реализация математических моделей использующих методы интегрирования в среде MATLAB
РОССИЙСКОЙ ФЕДЕРАЦИИ
БЛАГОВЕЩЕНСКИЙ ГОСУДАРСТВЕННЫЙ
ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
Физико-математический факультет
Кафедра информатики
РЕАЛИЗАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ, ИСПОЛЬЗУЮЩИХ способы ИНТЕГРИРОВАНИЯ, В СРЕДЕ
MATLAB
Курсовая работа
Выполнил: студент курса
Научный управляющий:
кандидат физико-
математических наук, доцент
Благовещенск 2008
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.. 3
1. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ В MATLAB.. 5
1.1 Численный способ. 9
1.2 Символьный способ. 11
2. MATLAB – СРЕДА МОДЕЛИРОВАНИЯ.. 15
3. РЕАЛИЗАЦИЯ ЭКОНОМИЧЕСКОЙ МОДЕЛИ ВЗАИМОРАСЧЁТОВ ПРЕДПРИЯТИЙ В СРЕДЕ MATLAB.. 16
ЗАКЛЮЧЕНИЕ.. 19
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ… 20
ПРИЛОЖЕНИЯ.. 21
ВВЕДЕНИЕ
Нереально представить для себя современную науку без широкого внедрения математического моделирования. Суть этого способа состоит в подмене настоящего объекта его «образом» — математической моделью. Этот способ дозволяет стремительно и «безболезненно» поменять объект, изучить его характеристики и Создание модели проходит в 3 шага: модель – метод – программка.
Рис. 1 – Создание модели
На первом шаге строится модель, более много отображающая характеристики объекта. Модель исследуется теоретическими способами, что дозволяет получить принципиальные подготовительные познания о объекте. 2-ой шаг содержит в себе разработку метода, для реализации модели на компе. Модель представляется в форме, комфортной для внедрения численных способов, определяется последовательность вычислительных и логических операций, которые нужно провести для нахождения разыскиваемых величин с данной точностью. На 3-ем шаге создаются программки, переводящие модель и метод на доступный компу язык. К ним предъявляются требования экономичности и адаптивности к особенностям решаемых задач и применяемых компов. Их можно именовать электрическим эквивалентом изучаемого объекта, уже подходящим для конкретного тесты на компе.
Целью данной курсовой работы является исследование приёмов численного и символьного интегрирования на базе математического пакета прикладных программ, также реализация математической модели, основанной на способе интегрирования.
1.
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ В
MATLAB
Вероятны два разных подхода к определению определённого интеграла.
ОПРЕДЕЛЕНИЕ 1: приращение F(b)-F(a) хоть какой из перевоплощенных функций F(x)+c при изменении аргумента от x=a до x=b именуют определённым интегралом от a до b функции F и обозначается  .
.
Причём функция F является первообразной для функции f на неком промежутке D, а числа а и b принадлежат этому промежутку. Это можно записать последующим образом:  , это формула Ньютона-Лейбница.
, это формула Ньютона-Лейбница.
Рис. 2 – Определённый интеграл

ОПРЕДЕЛЕНИЕ 2: Если при хоть какой последовательности разбиений отрезка [a;b] таковых, что δ=maxΔxi→0 (n→∞) и при любом выборе точек интегральная сумма σk=
интегральная сумма σk= f(εi) Δxi стремится к одному и тому же конечному лимиту А, то это число А и есть определённый интеграл, т.е Δxi=A(2). Где Δхi=xi-xi-1 (i=1,2,…,n) ε=maxΔxi – начало разбиения
f(εi) Δxi стремится к одному и тому же конечному лимиту А, то это число А и есть определённый интеграл, т.е Δxi=A(2). Где Δхi=xi-xi-1 (i=1,2,…,n) ε=maxΔxi – начало разбиения  случайная точка из отрезка [xi-1;xi]
случайная точка из отрезка [xi-1;xi]
сумма всех произведений f(εi)Δxi, (i=1,…,n). Ординарными словами, определенный интеграл есть предел интегральной суммы, число членов которой неограниченно растет, а каждое слагаемое стремится к нулю.
Рис. 3 – Геометрический смысл
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ:

Всякая непрерывная на отрезке [a,b] функция f интегрируема на отрезке [a,b], функция f неотрицательна, но определённый интеграл  численно равен S криволинейной трапеции, ограниченной графиком функции f, осью абсцисс и прямыми x=a и x=b,
численно равен S криволинейной трапеции, ограниченной графиком функции f, осью абсцисс и прямыми x=a и x=b,  .
.
Разглядим главные способы интегрирования: способ трапеций, способ прямоугольников и способ Симпсона.
Формула прямоугольников
сейчас разглядим 1-ый вид приближённого вычисления:
требуется вычислить определённый интеграл:  .
.
Пусть на отрезке [a,b] задана непрерывная функция y=f(x). Разделим отрезок [a,b], аналогично как в формуле трапеций: точками a=x0, x1, x2,…, xn=b на n равных частей длины Δх, где Δх=(b-a)/n.
Рис. 4 – Формула прямоугольников


Обозначим через y0, y1 ,y2,…, yn-1, yn
Y0=f(x0), y1=f(x1), y2=f(x2)…yn,=f(xn).
В данном методе подынтегральную функцию заменяем функцией, которая имеет ступенчатый вид.
Составим суммы: y0Δx+ y1Δx1+ y2Δx2…+yn-1Δx; Y1Δx+ y2Δx+…+ynΔx.
В итоге вычислений получаем конечную формулу прямоугольников:
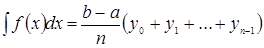
Формула трапеций
Возьмём определённый интеграл  , где
, где  — непрерывная подынтегральная функция, которую мы для наглядности будем полагать положительной. При вычислении интеграла при помощи формулы трапеций подынтегральная функция f заменяется функцией, график которой представляет собой ломанную линию звенья которой соединяют концы ординат yi-1 и yi (i=1,2,…,n).
— непрерывная подынтегральная функция, которую мы для наглядности будем полагать положительной. При вычислении интеграла при помощи формулы трапеций подынтегральная функция f заменяется функцией, график которой представляет собой ломанную линию звенья которой соединяют концы ординат yi-1 и yi (i=1,2,…,n).

Рис. 5 – Формула трапеций
Тогда площадь криволинейной трапеции, ограниченной линиями x=a, x=b, y=0, y=f(x), а означает (следуя из геометрического смысла), и
Рис. 6 – Разбиение трапеции

Площадь последней полосы слева равна произведению полусуммы основания на высоту
Итак, запишем произнесенное выше в математическом виде:
 – это и есть формула трапеций.
– это и есть формула трапеций.
Формула Симпсона (формула парабол).
Разделим отрезок [a;b] на чётное число равных частей n=2m. Площадь криволинейной трапеции, соответственной первым двум отрезкам [x0,x1], [x1,x2] и ограниченной данной кривой y=f(x), заменим площадью криволинейной трапеции, которая ограничена параболой 2-ой степени, проходящей через три точки M0[x0,y0], M1[x1,y1], M2[x2,y2] и имеющей ось, параллельную оси Oy (рис). Такую криволинейную трапецию будем именовать параболической трапецией.
Уравнение па

раболы с осью, параллельной оси Oy, имеет вид:  . Коэффициенты A, B и C совершенно точно определяются из условия, что парабола проходит через три данные точки. Подобные параболы строятся и для остальных пар отрезков. Сумма параболических трапеций и даст приближённое
. Коэффициенты A, B и C совершенно точно определяются из условия, что парабола проходит через три данные точки. Подобные параболы строятся и для остальных пар отрезков. Сумма параболических трапеций и даст приближённое 
сейчас разглядим способы решения интегралов при помощи программки Matlab.
1.1 Численный способ
Вычисление определенных интегралов.
Разглядим пример:  .
.
Сначала нужно сделать функцию, вычисляющую подынтегральное выражение.
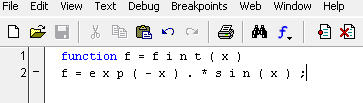
Для вычисления интеграла вызовем функцию quad, задав первым аргументом ссылку на функцию fint, а вторым и третьим — нижний и верхний пределы интегрирования.
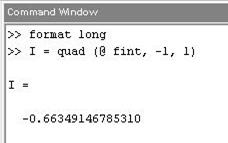
По дефлоту функция quad вычисляет приближенное конфигурации точности вычислений следует задать доп 4-ый аргумент:
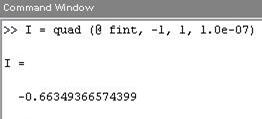
Вычисление двойных интегралов.
В MATLAB определена функция dblquad для приближенного вычисления двойных интегралов. Как и в случае вычисления определенных интегралов, следует написать файл-функцию для вычисления подынтегрального выражения. Вычислим интеграл:
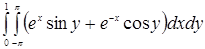
Как следует, функция обязана содержать два аргумента x и y:
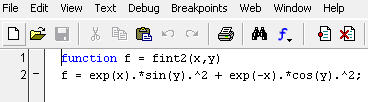
Функция dblquad имеет 5 входных аргументов. При ее вызове нужно учитывать, что первыми задаются пределы внутреннего интеграла по х, а вторыми — наружного по у:
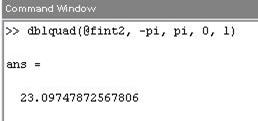
Интегралы, зависящие от параметра.
Функции quad и quadl разрешают отыскивать значения интегралов, зависящих от характеристик. Аргументами функции, вычисляющей подынтегральное выражение, обязана быть не только лишь переменная интегрирования, да и все характеристики. значения характеристик указываются через запятую, начиная с шестого аргумента quad либо quadl. [1, C.270]
Решим интеграл:
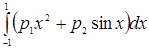
Зададим функцию
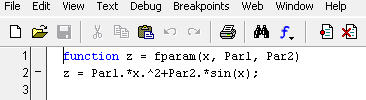
Используя quad, вычислим интеграл:
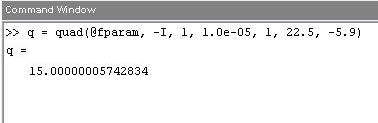
1.2 Символьный способ
Символьные переменные и функции являются объектами класса sym object, в отличие от числовых переменных, которые содержатся в массивах double array. Символьный объект создается с помощью функции syms. Команда
>> syms х a b
делает три символьные переменные х, а и b. Конструирование символьных функций от переменных класса sym object делается с внедрением обыденных арифметических операций и обозначений для интегрированных математических функций, к примеру:
>>f = (sin(x)+a)^2 * (cos(x)+b)^2/sqrt (абс(a+b))
f =
( sin(x)+a)2*(cos(x)+b)^2/абс(a+b)^(1/2)
Запись формулы для выражения в одну строчку не постоянно комфортна, наиболее естественный вид выражения выводит в командное окно функция pretty:
>>pretty(f)
2 2
(sin(x)+a) (cos(x)+b)
——————————-
1/2
| a + b |
Символьную функцию можно сделать без подготовительного объявления переменных с помощью sym, входным аргументом которой является строчка с выражением, заключенная в апострофы:
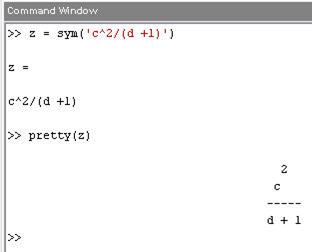
Symbolic Math Toolbox дозволяет работать как с неопределенными интегралами, так и с определенными. Неопределенные интегралы от символьных функций рассчитываются с помощью int, в качестве входных аргументов указываются символьная функция и переменная, по которой происходит интегрирование, к примеру:

Очевидно, функция int не постоянно может выполнить интегрирование. В неких вариантах int возвращает выражение для первообразной через особые функции, к примеру, посчитаем интеграл:
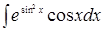
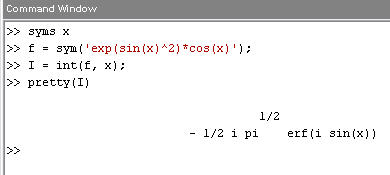
Ответ содержит так именуемую функцию ошибки, которая определяется интегралом с переменным верхним пределом:
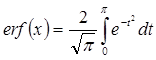
Не считая того, в приобретенное выражение заходит всеохватывающая единица, хотя подынтегральная функция вещественна. Требуются доп преобразования для заслуги окончательного результата.
Для нахождения определенного интеграла в символьном виде следует задать нижний и верхний пределы интегрирования, соответственно, в 3-ем и четвертом аргументах int:

Двойные интегралы рассчитываются повторным применением функции int. [1, C.780]
к примеру: 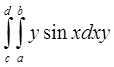
Определим символьные переменные а, b, с, d, x, у, подынтегральную функцию f от х и у и проинтегрируем поначалу по х, а потом по у:
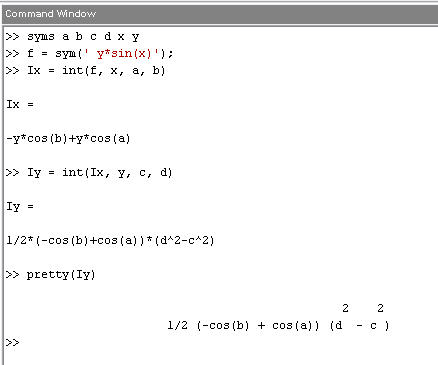
Аналогичным образом в символьном виде рассчитываются любые кратные интегралы.
2.
MATLAB – СРЕДА МОДЕЛИРОВАНИЯ
MATLAB (Matrix Laboratory – матричная лаборатория) это более развитая система программирования для научно-техническом расчетов, дополненная к истинному времени несколькими десятками наиболее личных приложений, относящихся к вычислительной арифметике, обработке инфы, экономике и ряду остальных разделов прикладной науки.
MATLAB предназначен для выполнения научных и инженерных расчетов на ПЭВМ. Эти расчеты могут иметь отношение к области аналитической геометрии, математической статистике, также к таковым научно – техническим приложениям, как спектральный и корреляционный анализ, расчет фильтров и прочее. В MATLAB реализованы традиционные численные методы решения уравнений, задач линейной алгебры, нахождения значений определенных интегралов, аппроксимации, решения систем либо отдельных дифференциальных уравнений. Для внедрения базисных вычислительных способностей довольно познания главных численных способов в рамках программки технических вузов. Решение особых задач, очевидно, нереально без соответственной теоретической подготовки; вообщем, сведения, изложенные в справочной системе, оказываются бесценным подспорьем для желающих без помощи других разобраться в широких способностях пакета. Подводя результат вышесказанному, можно прийти к выводу, что начинающий юзер MATLAB может в процессе работы улучшать свои познания как в области моделирования и численных способов, так и программирования, и визуализации данных. Не малым преимуществом MATLAB является открытость кода, что дает возможность опытным юзерам разбираться в запрограммированных методах и, по мере необходимости, изменять их. Вообщем, обилие набора функций MATLAB и Toolbox допускает решение большинства задач без каких-то подготовительных модификаций [6, С.5].
3. РЕАЛИЗАЦИЯ ЭКОНОМИЧЕСКОЙ МОДЕЛИ ВЗАИМОРАСЧЁТОВ ПРЕДПРИЯТИЙ В СРЕДЕ
MATLAB
Разглядим модель математической оценки с внедрением рублей и баксового эквивалента, при помощи 2-ух определенных интегралов, для вычисления которых употребляется формула трапеций.
В данном случае объектом исследования являются взаиморасчеты, в каких употребляются баксы и рубли. Контракт заключен меж 3-мя сторонами: заказчиком, генеральным подрядчиком и субподрядчиком.
Для анализа доходности сделок генерального подрядчика нас будут заинтересовывать последующие свойства экономической ситуации:
1) курс бакса в момент времени t;
2) уровень инфляции, характеризующийся коэффициентом момент вступления контракта в силу K(0), I(0).
Используя данные свойства, зададим уровень .
Если принять за базу уровень цен в момент вступления контракта в силу, т.е. I(0)=1, то уровень цен в момент времени t можно выразить так:
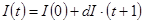
Запишем формулу современной цены непрерывного потока выплат подрядчику в рублях по текущему курсу бакса K(t) с учетом индекса I(t).
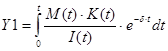
Запишем сейчас формулу современной цены непрерывного потока платежей субподрядчикам в рублях с учетом
Разность меж Y1 и Y2 даст современную стоимость потока наличности подрядчика в момент времени t.
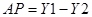
Если величина АР>0, означает, можно гласить и доходности сделок меж заказчиком, генеральным подрядчиком и субподрядчиком.
Определим все характеристики модели.
>>N=10000;
>>M=50000;
>>T=1;
>>δ=0.1;
>>dI=0.1763;
>>dK=0.85;
>>Io=1;
>>Ko=27.8;
Вычислим K(t) и I(t):
>> K(t) = 57.3
>> I(t) = 2.3526
Для удобства вычисления введём последующие обозначения:
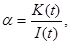
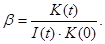
Перепишем интегралы Y1 и Y2:
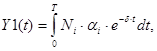
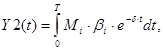
А их подынтегральные функции обозначим через S1(t) и S1(t) соответственно:
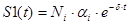
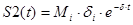
Вычислим S1(t) и S1(t):
>>S1= 2.2038
>>S2= 1.1019
Определим подынтегральную функцию интегрального сальдо наличности генерального подрядчика как функцию S(t).
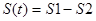
>>S(t)=1.1019
Крайним шагом вычислим интеграл по формуле трапеций:
 , где
, где  – шаг интегрирования
– шаг интегрирования
>>А=1.65285
Потому что интеграл А больше 0, то можно прийти к выводу о том, что контракт меж заказчиком, генеральным подрядчиком и субподрядчиком, является экономически прибыльным.
ЗАКЛЮЧЕНИЕ
Из данной работы видно, как ординарна и комфортна в использовании система Matlab. Для работы с ней нужно иметь самые простые способности работы на ПК .
Говоря о математических качествах MATLAB, необходимо отметить, что его обозначения весьма близки к тем, которые издавна употребляются в арифметике, и это приметно упрощает освоение бессчетных математических установок.
Этот пакет может употребляться во всех сферах вычислений начиная с самых обычных, заканчивая самыми сложными.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Ануфриев, И. Е. MATLAB 7: Самоучитель / Ануфриев, И. Е. Смирнов, А.Б. Смирнова, Е. Н. – СПб.: БХВ-Петербург, 2005. – 1104 с.
2. Выгодский, М. Я. Справочник по высшей арифметике / Выгодский, М. Я. – М.: АСТ: Астрель, 2005. – 991с.
3. Демидович, Б. П.Базы вычислительной арифметики / Демидович, Б. П. Марон, И. А. – М.: Наука, 1970. – 402с.
4. Масловская, А.Г. Главные принципы работы и конструирование интерфейса в Matlab : Практикум / Масловская, А. Г. – Благовещенск.: Амурский гос. ун-т, 2008. – 55с.
5. Масловская, А. Г. Численные способы. Моделирование на базе Matlab : Практикум / Масловская, А. Г. Черпак, Л. В. – Благовещенск.: Амурский гос. ун-т, 2006. – 120с.
6. Самарский, А. А. Математическое моделирование: Идеи. способы. Примеры / Самарский, А. А. Михайлов, А.П. – М.: Наука. Физматлит. 1997 – 320с.
7. Тарасевич, Ю.Ю. Математическое и компьютерное моделирование / Тарасевич, Ю.Ю. – М.: Едиториал УРСС, 2004. – 152с.
приложение 1
Определение характеристик экономической модели.

Приложение 2
Вычисление курса бакса и уровня цен, в момент времени
t
.
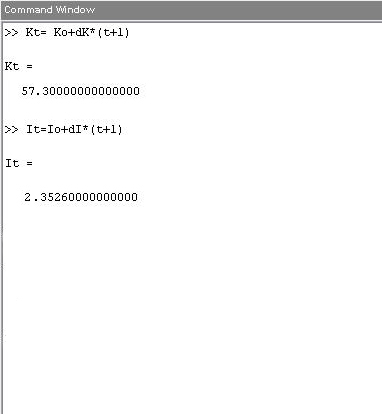
Приложение 3
Вычисление подынтегральных функций
S
1 и
S
2.
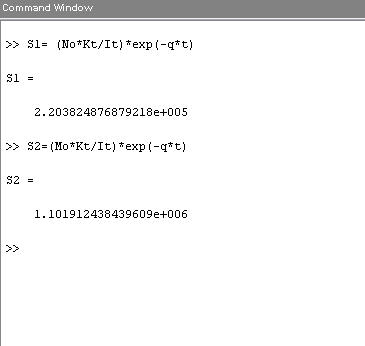
приложение 4
Вычисление интеграла по формуле трапеций.

]]>

