Учебная работа. Реферат: Акустические резонаторы
БЕЛОРУССКИЙ государственный УНИВЕРСИТЕТ
Факультет радиофизики и физической электроники
Реферат
Студента I курса 4-ой группы
Б.Никты
По теме:
Акустические резонаторы.
МИНСК 2001 г.
Акустические резонаторы.
Звуковыми волнами
или просто звуком
принято называть волны, воспринимаемые человеческим ухом. Диапазон звуковых частот лежит в пределах приблизительно от 20 Гц до 20 кГц. Волны с частотой менее 20 Гц называются инфразвуком
, а с частотой более 20 кГц — ультразвуком
. Волны звукового диапазона могут распространяться не только в газе, но и в жидкости (продольные волны) и в твердом теле (продольные и поперечные волны). однако волны в газообразной среде — среде нашего обитания — представляют особый интерес. Изучением звуковых явлений занимается раздел физики, который называют акустикой
.
При распространении звука в газе атомы и молекулы колеблются вдоль направления распространения волны. Это приводит к изменениям локальной плотности и давления p. Звуковые волны в газе часто называют волнами плотности или волнами давления.
При восприятии различных звуков человеческое ухо оценивает их прежде всего по уровню громкости, зависящей от потока энергии или интенсивности звуковой волны. Воздействие звуковой волны на барабанную перепонку зависит от звукового давления
, т.е. амплитуды p0
колебаний давления в волне. Человеческое ухо является совершенным созданием Природы, способным воспринимать звуки в огромном диапазоне интенсивностей: от слабого писка комара до грохота вулкана. Порог слышимости
соответствует значению p0
порядка 10-10
атм., т.е. 10-5
Па. При таком слабом звуке молекулы воздуха колеблются в звуковой волне с амплитудой всего лишь 10-7
см! Болевой порог
соответствует значению p0
порядка 10-4
атм. или 10 Па. Таким образом, человеческое ухо способно воспринимать волны, в которых звуковое давление изменяется в миллион раз. Так как интенсивность звука пропорциональна квадрату звукового давления, то диапазон интенсивностей оказывается порядка 1012
! такой огромный диапазон человеческого уха эквивалентен использованию одного и того же прибора для измерения диаметра атома и размеров футбольного поля.
Для сравнения укажем, что при обычных разговорах людей в комнате интенсивность звука приблизительно в 106
раз превышает порог слышимости, а интенсивность звука при рок-концерте приближается к болевому порогу.
Еще одной характеристикой звуковых волн, определяющей их слуховое восприятие, является высота звука
. Колебания в гармонической звуковой волне воспринимаются человеческим ухом как музыкальный тон
. Колебания высокой частоты воспринимаются как звуки высокого тона
, колебания низкой частоты — как звук низкого тона
. Звуки, издаваемые музыкальными инструментами, а также звуки человеческого голоса могут сильно различаться по высоте тона и по диапазону частот. Так, например, диапазон наиболее низкого мужского голоса — баса — простирается приблизительно от 80 до 400 Гц, а диапазон высокого женского голоса — сопрано — от 250 до 1050 Гц.
диапазон звуковых колебаний, соответствующий изменению частоты колебаний в два раза, называется октавой
. Голос скрипки, например, перекрывает приблизительно три с половиной октавы (196-2340 Гц), а звуки пианино — семь с лишним октав (27.5 — 4186 Гц).
При настройке музыкальных инструментов часто используется устройство, называемое камертоном
. Оно состоит из деревянного акустического резонатора и скрепленной с ним металлической вилки, настроенных в резонанс. При ударе молоточком по вилке вся система возбуждается и издает чистый музыкальный тон.
Акустическим резонатором является и гортань певца.
Резонаторы —
усилители колебаний. Явление акустического резонанса заключается в том, что акустическая система приводится в колебание, когда невдалеке от нее звучит другая акустическая система с частотой колебаний, совпадающей с собственной частотой первой.
Резонатором в акустике может служить натянутая струна, открытый или закрытый объем, например, в виде деревянного, стеклянного, металлического цилиндра (трубы), пластинка, закрепленная с одного конца, камертон и т.д. В резонаторе возбуждаются колебания даже от сравнительно слабых звуковых волн, падающих на него.
Почему же резонатор увеличивает интенсивность доходящих до него колебаний? Ответов может быть два:
· или резонатор собирает рассеянную в пространстве энергию,
· или усиление происходит за счет уменьшения продолжительности
колебаний.
Оба ответа справедливы.
В театрах древней Греции и Древнего Рима устанавливали так называемые «гармоники» — открытые объемы, горловина которых соединялась с окружающим пространством (рис. 1, а). Масса воздуха m в горловине приводилась в колебательное движение внешним звуковым давлением. Резонансная частота f0 определялась этой массой и гибкостью (сжимаемостью) c воздушного объема V резонатора. При резонансе скорость колебаний v в горле резонатора увеличивается, увеличивается и объемный поток vS ( S — площадь поперечного сечения горла). Ввиду того, что колебательная скорость падающей волны остается постоянной, для поддержания возрастающего объемного потока фронт падающей волны деформируется (рис.1, б). Деформация охватывает тем большую зону, чем больше скорость колебаний в горле. поэтому резонатор концентрирует значительно большую энергию, чем та, которая содержится в части падающей волны, приходящейся на площадь входного отверстия. после прекращения внешнего воздействия резонатор отдает накопленную энергию в окружающее пространство (рис. 1, в).
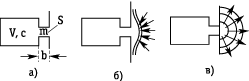
Рис.1
Принцип действия акустического резонатора.
- а) конструкция;
- б) деформация фронта падающей волны;
- в) отдача накопленной энергии в окружающее
пространство
Дается экспериментальное подтверждение второму предположению — увеличению интенсивности колебаний за счет уменьшения их продолжительности. Свободно подвешенный и возбужденный ударом камертон звучит 252 с, приложенный к мраморной доске — 115 с, приложенный к деревянной доске — 10 с. Особенно усиливаются колебания, если приложить камертон к ящику-резонатору с той же собственной частотой, что и у камертона. Однако продолжительность колебаний в этом случае еще более сокращается.
Итак, звук усиливается, но запасенная энергия исчерпывается быстрее. Степень усиления колебаний определяется добротностью резонатора, а ощущение громкости — интенсивностью колебаний и их продолжительностью. поэтому не следует преувеличивать эффективность действия «гармоник» древних театров на открытом воздухе или кувшинов-«голосников» древних православных храмов. Эти устройства создавали сравнительно небольшое усиление колебаний. Такие резонаторы иногда используют в современных акустических лабораториях.
Можно предположить, что замкнутые пространства под эстрадой концертных залов и под оркестровой ямой оперных театров также являются своеобразными резонаторами, усиливающими звучность. Аналогичную роль играют подвесные «мембранные потолки» концертных и театральных залов, разумеется, если они не отягощены помещенным на них грузом-засыпкой из камней и шлака. В отличие от резонаторов-сосудов, представляющих собой системы с сосредоточенными параметрами, пространства под эстрадой или подвесные потолки являются системами с распределенными параметрами, «многочастотными системами».
Связь собственной резонансной частоты объемных акустических резонаторов с их геометрическими размерами устанавливалась различными авторами, начиная с Гельмгольца. Внешнее несходство полученных выражений определяется различием некоторых исходных предпосылок, но рассчитанные значения f0 получаются примерно одинаковыми. Для резонаторов без горла (b=0) И.Г. Дрейзен приводит выражение


а Е. Скучик – выражение
причем a — радиус отверстия, V — объем. При а = 1 см и V = 500 см3 расчеты f0 по приведенным двум формулам дают соответственно значения 340 и 330 Гц.

И. Г. Дрейзен и Е. Скучик получили выражения для добротности Q объемного резонатора. По Дрейзену, усилительная способность резонатора определяется отношением звукового давления в горле резонатора p2 к звуковому давлению р1 в падающей волне:
причем k = 2p/l = 2pf/c0 — волновое число, V — объем резонатора.
По Е. Скучику,

Подставив в последнюю формулу данные предыдущего примера, получим

Очевидно, что резонатор будет отвечать на возбуждение с частотами, лежащими в некоторой полосе частот, но наибольшая интенсивность колебаний установится при совпадении частоты источника колебаний с собственной частотой резонатора.
Резонансные поглощающие конструкции.
В зависимости от добротности акустические резонаторы действуют либо как усилители звуковых колебаний, либо как высокоэффективные поглотители. При резонансе скорость движения частиц воздуха в горле резонатора максимальна. Если поместить в горле элемент активного сопротивления r, то из-за большой скорости колебаний v потери мощности Ра = v2r будут велики. Потери возникают ввиду трения частиц воздуха о стенки горла. Потери возрастут, если отверстие перегородить такой тканью, как марля.
Одиночные резонансные поглотители иногда используют для исправления АЧХ помещения в области нижних частот. Комбинации резонаторов в виде перфорированных листов (панелей), укрепленных на некотором расстоянии от стены или потолка помещения, на частоте резонанса поглощают 0,8 — 0,95 энергии падающей волны. В нашей стране высокоэффективные перфорированные звукопоглощающие конструкции были разработаны Г.Д. Малюжинцем и С.И. Ржевкиным.

Расчетные соотношения.
Резонансная частота перфорированной конструкции, как и для одиночного резонатора, определяется выражением
в котором S — площадь отверстия, b — длина горла (или, что то же самое, толщина листа), V — объем полости, равный произведению квадрата шага перфорации d на расстояние между листом и преградой d.

Большими коэффициентами поглощения обладают мембранные резонансные конструкции. Они состоят из тонких листов фанеры, закрепленных по периметру на жестком каркасе из деревянных брусьев. Падение звуковой волны вызывает изгибные колебания листа. Энергия волны тратится на вязкие потери (трение) между слоями фанеры, скрепленными клеем. Для увеличения потерь между стеной и листом помещают демпфирующий материал с большой вязкостью, например губчатую резину, поролоновые коврики, строительный войлок и т.п. Разновидностью мембранных конструкций являются щиты Г. Бекеши. Они представляют собой рамы, на которые натянут холст, клеенка, пластмассовая пленка. Для демпфирования колебаний используют подкладку из поролона, ваты, войлока. В отличие от перфорированных конструкций мембранные являются системой с распределенными параметрами. Максимумы поглощения получаются на резонансных частотах. Для натянутого с силой F материала мембраны резонансные частоты
где n — порядок резонансной частоты, l, b и d — длина, ширина и толщина материала, r — его плотность.

Пусть полотно размером 2 х 1 м, толщиной 0,2 мм и плотностью 200 г/м3 натянуто с силой 1,6 Н. Тогда резонансные частоты
следовательно, резонансные частоты будут 50, 100 Гц и т.д. Коэффициенты поглощения мембранных конструкций достигают:
· для фанеры и бумажно-слоистого пластика примерно 0,5;
· для щитов Бекеши — 0,8.
Отметим интересный факт. Г. Гельмгольц использовал набор резонаторов с разными резонансными частотами для анализа спектров звуковых колебаний. С помощью этого своеобразного анализатора Гельмгольц наблюдал, какие резонаторы отзываются на разные частотные составляющие спектра. Он же применил комбинации резонаторов для синтеза гласных звуков речи.
Экспериментальное исследование взаимодействия упругих волн
в акустическом резонаторе.
В.Е.Назаров, А.В.Радостин, И.А.Соустова
Институт прикладной физики ран
В акустике подробно изучены нелинейные эффекты, возникающие при распространении и взаимодействии упругих волн в твердых телах, уравнение состояния которых описываются 5-ти константной теорией упругости. Подобный подход, как правило, справедлив для описания однородных сред. Для микронеоднородных сред, в частности горных пород, содержащих различные дефекты (дислокации, зерна, трещины и т.д.) даже при относительно небольших деформациях, уравнение состояния часто характеризуется неоднозначной (гистерезисной) зависимостью «напряжение – деформация» и может также содержать диссипативную нелинейность. При распространении интенсивных упругих волн в таких средах наблюдаются нелинейные эффекты: амплитудно-зависимые потери, изменение скорости волны, генерация высших гармоник и т.д. наиболее сильно эти эффекты проявляются в акустических резонаторах. Такие эксперименты проводились с некоторыми металлами и горными породами [1-3]. В настоящей работе представлены результаты экспериментальных исследований влияния мощной волны накачки на слабую волну в резонаторе из песчаника — горной породы, встречающейся в местах добычи нефти и газа. эксперименты проводились со стержневым резонатором диаметром d
= 2.5см и длиной L
= 28см. Блок-схема измерительной установки представлена рис.2.
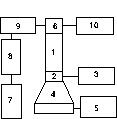
Рис.2
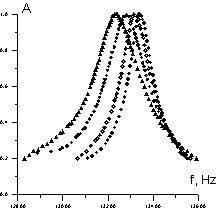
Рис.3
Пьезокерамический излучатель слабой волны (2) был приклеен к торцу образца (1) и массивному (М
= 2 кг) титановому концентратору (4), являющемуся излучателем мощной волны накачки (ее минимальный уровень превышал максимальный уровень слабой волны примерно на 30 дБ), так что граничное условие на этом торце резонатора было близко к условию на абсолютно жесткой поверхности. К другому концу стержня приклеивался пьезоакселерометр (6) достаточно малой массы, так что эта граница была близка к акустически мягкой. Для таких резонаторов спектр собственных частот определяется следующим выражением: fn
=c0
(2n‑1)/4L
, где c0
— скорость продольной волны в стержне, n
= 1,2…- номер продольной моды резонатора. С пьезоакселерометра сигнал поступал на спектроанализатор (10) для измерения амплитуды накачки, а также через режекторный фильтр (9), подавляющий сигнал на частоте накачки на 30 дБ, на селективный вольтметр (8) и осциллограф (7), где производилось измерение уровня слабого сигнала. Собственные частоты первых продольных мод резонатора при малых амплитудах возбуждения составляли соответственно 2250 Гц, 6800 Гц, 10150 Гц и 16650 Гц, а добротности — 45, 90, 81 и 93. таким собственным частотам соответствует c0
»2500 м/с. Измерения проводились для слабой волны на 4-й моде резонатора и для накачки на 1-й моде, а также — наоборот. На рис.3 приведены резонансные кривые для слабой волны на 4-й моде в присутствии накачки на 1-й моде при различных ее амплитудах. Видно, что с ростом амплитуды волны накачки происходит сдвиг резонансной частоты и расширение резонансной кривой, т.е. уменьшение добротности резонатора
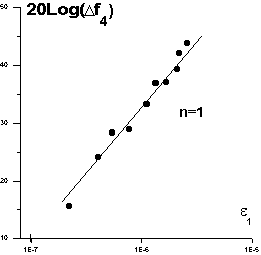
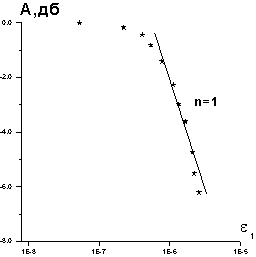
Рис.4
Рис.5
На рис.4 в логарифмическом масштабе приведена зависимость сдвига резонансной частоты D
F
от амплитуды деформации волны накачки e
1
,
из которого следует, что D
F
µ
e
1
.
На рис.5 приведена зависимость амплитуды слабой волны A
(в резонансе) от e
1
,
из которого видно, что A
µ
e
1
.
аналогичные зависимости наблюдались и в случае возбуждения слабой волны на 1-й моде резонатора, а накачки — на 4-й.
Аналитическое описание сдвига резонансной частоты проведено в рамках уравнения состояния, содержащего упругую нелинейность:
,
где E
— модуль Юнга, f(
e
)
— малая нелинейная поправка (|f(
e
)|<<|
e
|
), a
— коэффициент диссипации, r
— плотность. С помощью методов, изложенных в работах [1,4], получена резонансная кривая стержня для слабой волны на 4-й моде резонатора при накачке на 1-й моде:
,
где A0
— амплитуда слабой волны, создаваемой излучателем, d
=
w
n
—
w
— расстройка частоты от резонанса, B0
=
ў
e
>=
g
e
1
, где g
— эффективный параметр упругой нелинейности песчаника. Из сравнения экспериментальной и аналитической зависимости получаем оценку для параметра упругой нелинейности песчаника: g
»2Ч103
. Отметим, что полученное значение параметра упругой нелинейности существенно превышает характерные значения для однородных сред (g
<10).
таким образом, уравнение состояния, содержащее упругую нелинейность, описывает только сдвиг резонансной частоты, и не описывает уменьшение добротности резонатора для слабой волны в поле мощной волны накачки. Для объяснения этого эффекта необходимо предположить, что песчаник обладает также и диссипативной акустической нелинейностью.
Работа выполнена при поддержке РФФИ (гранд 96-15-96603).
Использованная литература:
1) «Три взгляда на акустику помещений» А.П. Ефимов, журнал «Install Pro Magazine», 2000 г.
2) Назаров В.Е., Островский Л.А., Соустова И.А., Сутин А.М. «Акустический журнал», №3,1988 г.
3) «
Физика металлов и металловедение» Назаров В.Е. 1992.

