Учебная работа. Курсовая работа: Метод Ньютона и его модификации решения систем нелинейных уравнений
Сочинский муниципальный институт туризма и курортного дела
Факультет информационных технологий и арифметики
Кафедра общей арифметики
Курсовая работа по дисциплине
«Численные способы»
на тему:
«Способ Ньютона и его модификации решения систем нелинейных уравнений»
Выполнила:
студентка 3 курса
группы 06-ИНФ
Лавренко М.В.
Проверил:
доцент, кандидат
педагогических наук
Иванов И.А.
Сочи 2009
СОДЕРЖАНИЕ.
ВВЕДЕНИЕ.3
1.
способ НЬЮТОНА И ЕГО РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.4
ВЕКТОРНАЯ ЗАПИСЬ НЕЛИНЕЙНЫХ СИСТЕМ.5
1.2. ОСНОВНАЯ ТЕОРЕМА О СХОДИМОСТИ МЕТОДА НЬЮТОНА.7
1.3.
КРИТЕРИЙ ОКОНЧАНИЯ.8
2.
способ НЬЮТОНА И ЕГО РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.11
2.1.
ОПИСАНИЕ МЕТОДА.11
2.2.
СХОДИМОСТЬ МЕТОДА.12
2.3.
ТРУДНОСТИ ИСПОЛЬЗОВАНИЯ.14
3.
МОДЕФИКАЦИЯ МЕТОДА НЬЮТОНА.15
3.1.
УПРОЩЁННЫЙ способ НЬЮТОНА.15
3.2.
ИСПОЛЬЗОВАНИЕ ФОРМУЛ ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ.16
3.3.
способ ЛОЖНОГО ПОЛОЖЕНИЯ.17
3.4.
метод СЕКУЩИХ.17
3.5.
МЕТОД СТЕФФЕНСЕНА.18
4.
ЧИСЛЕННЫЙ ПРИМЕР. 20
5.
ЛИСТИНГ ПРОГРАММЫ НА ЯЗЫКЕ MATHCAD.. 21
ЗАКЛЮЧЕНИЕ. 23
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.24
ВВЕДЕНИЕ.
В связи с развитием новейшей вычислительной техники инженерная практика наших дней все почаще и почаще встречается с математическими задачками, четкое решение которых получить очень трудно либо нереально. В этих вариантах обычно прибегают к тем либо другим приближенным вычислениям. Вот почему приближенные и численные способы математического анализа получили за крайние годы обширное развитие и заполучили только принципиальное
В данной курсовой работе рассматривается именитый способ Ньютона и его модификация решения систем нелинейных уравнений. Решение систем нелинейных уравнений – одна из тяжелых задач вычислительной арифметики. Трудность заключается в том, чтоб найти: имеет ли система решение, и, если – да, то сколько. Изучается сходимость основного и облегченного способов Ньютона и способа, получаемого из способа Ньютона применением итерационного процесса для приближенного воззвания матриц Якоби.
А так же кратко описываются: способы неверного положения, способ секущих, способ Стеффенсена, который почаще оказывается наилучшим выбором для решения систем нелинейных уравнений нежели способ секущих либо способ неверного положения.
1. способ НЬЮТОНА И ЕГО РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Именитый способ Ньютона является одним из более действенных способов решения самых различных нелинейных задач. Расчётную формулу способа можно получить, используя разные подходы. Разглядим два из их.
1) способ касательных.
Выведем расчётную формулу способа для решения нелинейного уравнения  из обычных геометрических суждений. Пусть
из обычных геометрических суждений. Пусть  — данное изначальное приближение к корню
— данное изначальное приближение к корню  . В точке
. В точке  с координатами
с координатами  проведём касательную к графику функции
проведём касательную к графику функции  и за новое приближение
и за новое приближение  примем абсциссу точки пересечения данной для нас касательной с осью
примем абсциссу точки пересечения данной для нас касательной с осью  . Аналогично за приближение
. Аналогично за приближение  примем абсциссу точки пересечения с осью
примем абсциссу точки пересечения с осью  касательной, проведённой к графику в точке
касательной, проведённой к графику в точке  с координатами
с координатами  . Продолжая этот процесс дальше, получим последовательность
. Продолжая этот процесс дальше, получим последовательность  приближённой к корню
приближённой к корню  .
.
Уравнение касательной, проведённой к графику функции  в точке
в точке  имеет вид:
имеет вид:
 . (1.1)
. (1.1)
Полагая в равенстве (1.1)  , замечаем, что при выполнении условия
, замечаем, что при выполнении условия  абсцисса
абсцисса  точки пересечения касательной с осью
точки пересечения касательной с осью  удовлетворяет равенству:
удовлетворяет равенству:
 . (1.2)
. (1.2)
Выражая из него  , получаем расчётную формулу
, получаем расчётную формулу
:
 ,
,  . (1.3)
. (1.3)
Благодаря таковой геометрической интерпретации этот способ нередко именуют
.
ВЕКТОРНАЯ ЗАПИСЬ НЕЛИНЕЙНЫХ СИСТЕМ.
Пусть требуется решить систему уравнений
 (1)
(1)
где — данные, нелинейные (посреди их могут быть и линейные)
— данные, нелинейные (посреди их могут быть и линейные)
вещественнозначные функции
вещественных переменных  . Обозначив
. Обозначив
 ,
, 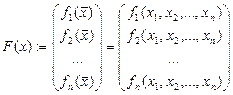 ,
, 
данную систему (2.1) можно записать одним уравнением
 (2)
(2)
относительно векторной функции
векторного аргумента х. Таковым образом, начальную задачку можно разглядывать как задачу о нулях нелинейного отображения  В данной для нас постановке она является прямым обобщением главный задачки предшествующей главы — задачки построения способов нахождения нулей одномерных нелинейных отображений. Практически это та же задачка, лишь в местах большей размерности. Потому можно как поновой строить способы ее решения на базе разработанных выше подходов, так и производить формальный перенос выведенных для скалярного варианта расчетных формул. В любом случае следует позаботиться о правомочности тех либо других операций над векторными переменными и векторными функциями, также о сходимости получаемых таковым методом итерационных действий. Нередко аксиомы сходимости для этих действий являются элементарными обобщениями соответственных результатов, приобретенных для способов решения скалярных уравнений. Но не все результаты и не все способы можно перенести со варианта
В данной для нас постановке она является прямым обобщением главный задачки предшествующей главы — задачки построения способов нахождения нулей одномерных нелинейных отображений. Практически это та же задачка, лишь в местах большей размерности. Потому можно как поновой строить способы ее решения на базе разработанных выше подходов, так и производить формальный перенос выведенных для скалярного варианта расчетных формул. В любом случае следует позаботиться о правомочности тех либо других операций над векторными переменными и векторными функциями, также о сходимости получаемых таковым методом итерационных действий. Нередко аксиомы сходимости для этих действий являются элементарными обобщениями соответственных результатов, приобретенных для способов решения скалярных уравнений. Но не все результаты и не все способы можно перенести со варианта
= 1 на вариант
≥2. к примеру, тут уже не будут работать способы дихотомии, так как огромное количество векторов не упорядочено. В то же время, переход от
= 1 до
2 заносит в задачку нахождения нулей нелинейного отображения свою специфику, учет которой приводит к новеньким способам и к разным модификациям уже имеющихся. А именно, большая вариативность способов решения нелинейных систем связана с многообразием методов, которыми можно решать линейные алгебраические задачки, возникающие при пошаговой линеаризации данной нелинейной вектор-функции
2) способ линеаризации.
С более общих позиций способ Ньютона можно разглядывать как итерационный способ, использующий специальную линеаризацию задачки и позволяющий свести решение начального нелинейного уравнения к решению последовательности линейных уравнений.
Пусть приближение  уже получено. Представим функцию в округи точки
уже получено. Представим функцию в округи точки  по формуле Тейлора:
по формуле Тейлора:
 . (1.4)
. (1.4)
тут  — некая точка, расположенная меж
— некая точка, расположенная меж  и
и  . Заменяя в уравнении
. Заменяя в уравнении  функцию
функцию  главной линейной частью разложений (1.4), получим линейное уравнение:
главной линейной частью разложений (1.4), получим линейное уравнение:
 . (1.5)
. (1.5)
Принимая решение уравнения (5) за новое приближение  , приходим к формуле (1.3).
, приходим к формуле (1.3).
1.2. ОСНОВНАЯ ТЕОРЕМА О СХОДИМОСТИ МЕТОДА НЬЮТОНА.
Аксиома 1.
 ,
,  , (1.6)
, (1.6)
где  ,
,
.
Следствием оценки (6) является априорная оценка:
 ,
,  , (1.7)
, (1.7)
в какой  .
.
Потому что  (по определению обычного корня), то в силу непрерывности функции
(по определению обычного корня), то в силу непрерывности функции  и
и  найдётся
найдётся  — округа корня, в какой при неких неизменных
— округа корня, в какой при неких неизменных  и
и  выполнены неравенства
выполнены неравенства  .
.
Пусть
, где  . Подставляя
. Подставляя  в (1.4), получим равенство:
в (1.4), получим равенство:
 ,
,
в каком  . Вычитая из него равенство (1.2), имеем
. Вычитая из него равенство (1.2), имеем
 .
.
Тогда, приравняв модули обеих частей этого равенства и используя условия ограниченности  и
и  , приходим к неравенству:
, приходим к неравенству:
 ,
,
откуда следует справедливость оценки (1.6).
Таковым образом, при выбирании исходного приближения из довольно малой округи корня способ Ньютона сходится квадратично. Это значит, что на каждой итерации число верных цифр приближения приблизительно умножается.
Приведённые в аксиоме 1 оценки погрешности являются априорными и их внедрение в практике вычислений для количественной оценки погрешности неэффективно либо почаще всего нереально.
1.3. КРИТЕРИЙ ОКОНЧАНИЯ.
На практике лучше внедрение обычной апостериорной оценки:
 , (1.8)
, (1.8)
справедливость которой обосновывается последующим утверждением.
Аксиома 2.
(8).
Из оценки (1.7) следует, что  . Потому, применяя неравенство (6), получим цепочку неравенств:
. Потому, применяя неравенство (6), получим цепочку неравенств:
 ,
,
из которой вытекает оценка (1.8).
наличие оценки (1.8) дозволяет сконструировать последующий практический аспект окончания итерации способа Ньютона. При данной точности  вычисления необходимо вести до того времени, пока не окажется выполнимым равенство:
вычисления необходимо вести до того времени, пока не окажется выполнимым равенство:
 . (1.9)
. (1.9)
Пример 1.
Используя способ Ньютона, найдём с точностью  положительный корень уравнения
положительный корень уравнения  .
.
 Для
Для  имеем
имеем  . Разумеется, что
. Разумеется, что  , т.е.
, т.е.  -простой корень. Возьмём изначальное приближение
-простой корень. Возьмём изначальное приближение  и будем делать итерации способа Ньютона по формуле:
и будем делать итерации способа Ньютона по формуле:
 .
.
Результаты первых итераций с 10 знаками мантиссы приведены в табл. 1.
Табл. 1


















При  вычисления следует закончить, и опосля округления получим
вычисления следует закончить, и опосля округления получим  .
.
Сопоставление результатов итераций со значением  указывает, что приближения
указывает, что приближения  содержат 1, 3, 6 верных означающих цифр соответственно. Это подтверждает отмеченный ранее факт, что при каждой итерации способа Ньютона число верных означающих цифр приблизительно умножается.
содержат 1, 3, 6 верных означающих цифр соответственно. Это подтверждает отмеченный ранее факт, что при каждой итерации способа Ньютона число верных означающих цифр приблизительно умножается.
Пример 2.
Используя способ Ньютона, укажем итерационный процесс вычисления  , где
, где  ,
,  — натуральное число.
— натуральное число.
По определению,  — это неотрицательная величина, удовлетворяющая равенству
— это неотрицательная величина, удовлетворяющая равенству  . Таковым образом, задачка сводится к вычислению положительного корня уравнения
. Таковым образом, задачка сводится к вычислению положительного корня уравнения  , где
, где  . Итерационная формула способа Ньютона имеет вид:
. Итерационная формула способа Ньютона имеет вид:
 . (1.10)
. (1.10)
2. способ НЬЮТОНА И ЕГО РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
2.1. ОПИСАНИЕ МЕТОДА.
Обобщим способ Ньютона, изложенный в пт 1 для решения 1-го нелинейного уравнения, на решение систем нелинейных уравнений. При всем этом будем исходить из трактовки способа Ньютона как способа линеаризации.
Представим, что исходя из исходного приближения  к решению
к решению  построены приближения
построены приближения  . Заменим в системе
. Заменим в системе

каждую из функций  линейной частью её разложения по формуле Тейлора в точке
линейной частью её разложения по формуле Тейлора в точке  :
:
 .
.
В итоге придём к системе линейных алгебраических уравнений:
 ,
,
 ,
,
. . . . . . . . . . . . . . .
 ,
,
имеющей в матричной форме записи вид:
 . (2.1)
. (2.1)
тут  — матрица Якоби.
— матрица Якоби. 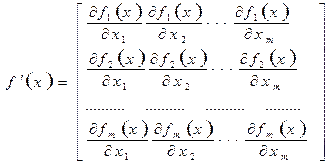 .
.
Представим, что матрица  невырожденная, т.е. существует оборотная матрица
невырожденная, т.е. существует оборотная матрица  . Тогда система (2.1) имеет единственное решение, которое принимается за еще одно приближение
. Тогда система (2.1) имеет единственное решение, которое принимается за еще одно приближение  к решению
к решению  . Таковым образом, приближение
. Таковым образом, приближение  удовлетворяет равенству:
удовлетворяет равенству:
 , (2.2)
, (2.2)
выражая из которого  , выводим итерационную формулу способа Ньютона:
, выводим итерационную формулу способа Ньютона:
 . (2.3)
. (2.3)
Замечание.
Формула (2.3) подразумевает внедрение трудоёмкой операции воззвания матрицы, потому конкретное её внедрение для вычисления  почти всегда нецелесообразно. Обычно заместо этого решают эквивалентную системе (2.2) систему линейных алгебраических уравнений:
почти всегда нецелесообразно. Обычно заместо этого решают эквивалентную системе (2.2) систему линейных алгебраических уравнений:
 (2.4)
(2.4)
относительно поправки  . Потом считают:
. Потом считают:
 (2.5)
(2.5)
2.2. СХОДИМОСТЬ МЕТОДА.
Сформулируем основную аксиому о сходимости способа Ньютона.
Аксиома 3.
Пусть в некой округи решения  системы
системы
функции  два раза безпрерывно дифференцируемы и матрица
два раза безпрерывно дифференцируемы и матрица  невырождена. Тогда найдётся таковая малая
невырождена. Тогда найдётся таковая малая  — округа решения
— округа решения  , что при случайном выборе исходного приближения
, что при случайном выборе исходного приближения  из данной для нас округи итерационная последовательность способа Ньютона не выходит за границы округи и справедлива оценка:
из данной для нас округи итерационная последовательность способа Ньютона не выходит за границы округи и справедлива оценка:
 ,
,  .
.
Эта оценка значит, что способ сходится с квадратичной скоростью.
Квадратичная скорость сходимости способа Ньютона дозволяет употреблять обычной практический аспект окончания:
 . (2.6)
. (2.6)
Пример 3.
Используя способ Ньютона, найдём с точностью  решение
решение  ,
,  системы
системы  .
.
Возьмём  ,
,  и будем вести вычисления по формулам (2.4), (2.5), в каких
и будем вести вычисления по формулам (2.4), (2.5), в каких
 ,
, 
 .
.
Результаты вычислений с шестью знаками мантиссы приведены в табл. 2.
Табл. 2















При  аспект окончания
аспект окончания  производится и можно положить
производится и можно положить  ,
,  .
.
2.3. ТРУДНОСТИ ИСПОЛЬЗОВАНИЯ.
Трудности использования способа Ньютона не только лишь сохраняются, да и усугубляются. Во-1-х, возникает неувязка вычисления на каждой итерации матрицы  из
из  личных производных, что {само по себе} может оказаться очень сложным делом. Во-2-х, обостряется неувязка нахождения неплохого исходного приближения. Её решить в многомерном случае еще сложнее, чем в одномерном.
личных производных, что {само по себе} может оказаться очень сложным делом. Во-2-х, обостряется неувязка нахождения неплохого исходного приближения. Её решить в многомерном случае еще сложнее, чем в одномерном.
3. МОДЕФИКАЦИЯ МЕТОДА НЬЮТОНА.
Если оценивать свойство способа Ньютона лишь по числу нужных итераций, то следовало бы прийти к выводу о том, что этот способ стоит использовать постоянно, когда он сходится. На практике для заслуги разумной точности  при выбирании довольно неплохого исходного приближения
при выбирании довольно неплохого исходного приближения  требуется, как правило, 3-5 итераций.
требуется, как правило, 3-5 итераций.
Но при оценке общеё трудоёмкости способа следует учесть, что на каждой итерации требуется выполнение последующей доборной работы:
1) вычисление  компонент вектора
компонент вектора  ;
;
2) вычисление  компонент матрицы Якоби
компонент матрицы Якоби  ;
;
3) решение системы линейных алгебраических уравнений (2.4).
Существует огромное число модификаций способа Ньютона, позволяющих в тех либо других ситуациях понизить его трудоёмкость или избежать необходимости вычисления производных. Разглядим коротко некие из таковых модификаций.
3.1. УПРОЩЁННЫЙ способ НЬЮТОНА.
Заменим в расчётных формулах способа Ньютона (2.4), (2.5) матрицу  , зависящую от
, зависящую от  , неизменной матрицы
, неизменной матрицы  . В итоге получим расчётные формулы
. В итоге получим расчётные формулы
:
 , (3.1)
, (3.1)
 . (3.2)
. (3.2)
Этот способ сходится со скоростью геометрической прогрессии, если изначальное приближение  выбрано довольно близким к решению
выбрано довольно близким к решению  , причём знаменатель прогрессии
, причём знаменатель прогрессии  тем меньше, чем поближе
тем меньше, чем поближе  к
к  .
.
По сопоставлению с способом Ньютона число итераций, нужное для заслуги данной точности  , значительно растет. Тем не наименее общие вычислительные Издержки могут оказаться меньше. Предпосылки этого состоят в последующем. Во-1-х, вычисление матрицы Якоби делается тут лишь один раз; во-2-х при использовании упрощённого способа Ньютона (3.1), (3.2) неоднократно решается система линейных уравнений с фиксированной матрицей
, значительно растет. Тем не наименее общие вычислительные Издержки могут оказаться меньше. Предпосылки этого состоят в последующем. Во-1-х, вычисление матрицы Якоби делается тут лишь один раз; во-2-х при использовании упрощённого способа Ньютона (3.1), (3.2) неоднократно решается система линейных уравнений с фиксированной матрицей  и разными правыми частями. Это значит, что при решении систем (3.1) способом Гаусса может быть применение LU– разложения матрицы
и разными правыми частями. Это значит, что при решении систем (3.1) способом Гаусса может быть применение LU– разложения матрицы  , которое резко уменьшает число операций, нужных для вычисления
, которое резко уменьшает число операций, нужных для вычисления  .
.
3.2. ИСПОЛЬЗОВАНИЕ ФОРМУЛ ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ.
Достаточно нередко вычисление производных  , являющихся элементами матрицы
, являющихся элементами матрицы  , затруднено либо совершенно нереально. В таковой ситуации для приближения вычисления производных можно употреблять формулы численного дифференцирования.
, затруднено либо совершенно нереально. В таковой ситуации для приближения вычисления производных можно употреблять формулы численного дифференцирования.
к примеру, можно употреблять последующую конечно-разностную аппроксимацию производной:
 .
.
характеристики  — это
— это
.
Если в расчётных формулах способа Ньютона (2.4), (2.5) поменять матрицу  аппроксимирующей её матрицей
аппроксимирующей её матрицей  с элементами
с элементами  , то получим последующий итерационный способ:
, то получим последующий итерационный способ:
 , (3.3)
, (3.3)
 . (3.4)
. (3.4)
В простом варианте этого способа шаги  не зависят от
не зависят от  . Отметим, что выбор величины шагов представляет собой не весьма ординарную задачку. С одной стороны, они должны быть довольно малыми, чтоб матрица
. Отметим, что выбор величины шагов представляет собой не весьма ординарную задачку. С одной стороны, они должны быть довольно малыми, чтоб матрица  отлично приближала матрицу
отлично приближала матрицу  , с иной стороны, они не могут быть весьма малы, та как в этом случае воздействие погрешностей вычисления функций
, с иной стороны, они не могут быть весьма малы, та как в этом случае воздействие погрешностей вычисления функций  на погрешность формулы (3.3) численного дифференцирования становится чертовским (производится вычитание близких приближённых чисел).
на погрешность формулы (3.3) численного дифференцирования становится чертовским (производится вычитание близких приближённых чисел).
Последующие три способа можно разглядывать как варианты способа (3.3), (3.4), в каких реализованы особые подходы к вычислению вектора  . Для того чтоб приведённые ниже рассуждения были формально корректными, в формуле (3.3) положим
. Для того чтоб приведённые ниже рассуждения были формально корректными, в формуле (3.3) положим  , если оказалось, что
, если оказалось, что  .
.
3.3. способ ЛОЖНОГО ПОЛОЖЕНИЯ.
Пусть  — фиксированный вектор. Положим
— фиксированный вектор. Положим  . Тогда формулы (3.3), (3.4) определяют способ неверного положении, владеющий линейной скоростью сходимости в случае, если вектор
. Тогда формулы (3.3), (3.4) определяют способ неверного положении, владеющий линейной скоростью сходимости в случае, если вектор  и изначальное приближённое
и изначальное приближённое  выбраны довольно близко к решению.
выбраны довольно близко к решению.
3.4. способ СЕКУЩИХ.
Можно связать задание последовательности  с какой-нибудь сходящейся к нулю векторной последовательностью, к примеру, с последовательность невязок
с какой-нибудь сходящейся к нулю векторной последовательностью, к примеру, с последовательность невязок  либо поправок
либо поправок  . Так, полагая
. Так, полагая  , где
, где
, a
…, приходим к простейшему способу секущих — обобщению скалярного способа секущих:
 , (3.5)
, (3.5)
где
 ,
,
=1,2,3,… .
Этот способ является двухшаговым и просит задания 2-ух исходных точек  и
и  . При п = 1 сходимость способа (3.5) имеет порядок
. При п = 1 сходимость способа (3.5) имеет порядок  . Можно рассчитывать на такую же скорость и в многомерном случае.
. Можно рассчитывать на такую же скорость и в многомерном случае.
К способу секущих так же, как и к способу Ньютона, можно применить пошаговую аппроксимацию оборотных матриц на базе способа Шульца. Расчетные формулы данной для нас модификации просто выписать, заменив в совокупы формул ААМН (аппроксимаиионный аналог способа Ньютона)  матрицу
матрицу  на матрицу
на матрицу
 из (3.5).
из (3.5).
3.5. способ
СТЕФФЕНСЕНА.
Вычисления по способу Стеффенсена создают по формулам (3.3), (3.4), где  .
.
Замечательно то, что хотя этот способ не просит вычисления производных и в отличие от способа секущих является одношаговым, он, как и способ Ньютона, владеет свойством квадратичной сходимости. правда, как и в способе Ньютона, его применение затруднено необходимостью выбора неплохого исходного приближения.
По-видимому, для решения нелинейных систем вида  способ Стеффенсена почаще кажется наилучшим выбором, чем способ секущих либо способ неверного положения.
способ Стеффенсена почаще кажется наилучшим выбором, чем способ секущих либо способ неверного положения.
Как и в одномерном случае способы секущих и Стеффенсена теряют устойчивость поблизости решения (практически это происходит при попадании приближения  в область неопределённости решения
в область неопределённости решения  ). Потому при использовании этих способов принципиально впору закончить выполнение итераций.
). Потому при использовании этих способов принципиально впору закончить выполнение итераций.
4. ЧИСЛЕННЫЙ ПРИМЕР

Изначальное приближение:

Вектор-функция:

Матрица Якоби вектор-функции:

Вычисляем корень по формуле способа Ньютона c точностью  :
:

k






0
0
-1
-0.841
0
-1.06 0.54
0 -2
-0.944 -0.255
0 -0.5
-0.794
-1
0.794>
1
-0.794
-1
0.295
0.63
-1.821 -0.221
-1.588 -2
-0.608 0.067
0.482 -0.553
-0.657
-0.794
0.247>
2
-0.657
-0.794
0.058
0.062
-1.48 0.12
-1.314 -1.588
-0.633 -0.048
0.524 -0.59
-0.617
-0.788
0.040>
3
-0.617
-0.788
-0.0000597
0.011
-1.441 0.159
-1.234 -1.588
-0.639 -0.064
0.497 -0.58
-0.616
-0.788
0.001=
4
-0.616
-0.788
0.000522
0.0004
-1.434 0.166
-1.232 -1.576
-0.639 -0.067
0.5 -0.582
-0.616
-0.788
0<
Ответ: 
5. ЛИСТИНГ ПРОГРАММЫ НА ЯЗЫКЕ
MATHCAD
Вводим вектор функцию:

Функция iter(x,y) вычисляет последующее приближение к корню по формуле Ньютона  , где
, где
 ,
,
 ,
,
 ,
,
 :
:

Функция norma(x,y,x1,y1) вычисляет норму меж текущим и последующим приближением:

Функция Newton(x,y,eps) находит решение системы уравнений с точностью до eps:

Найдем решение данной системы нелинейных уравнений при исходном приближении x=0, y=-1, с точностью до 0.001:


Приобретенное решение совпадает с рассчитанным.
ЗАКЛЮЧЕНИЕ
В данной курсовой работе был представлен способ Ньютона. Если оценивать свойство способа по числу нужных итераций, то следовало бы отметить, что этот способ стоит использовать постоянно, когда он сходится. Трудность использования способа Ньютона не только лишь сохраняются при применении его к решению систем нелинейных уравнений, да и усугубляются из-за возникающей препядствия вычисления на каждой итерации матрицы  из
из  личных производных, что {само по себе} может оказаться очень сложным делом.
личных производных, что {само по себе} может оказаться очень сложным делом.
Существует огромное число модификаций способа Ньютона, позволяющих в тех либо других ситуациях понизить его трудоёмкость или избежать необходимости вычисления производных. Такие модификации были также рассмотрены в данной курсовой работе: упрощённый способ Ньютона, использования формул численного дифференцирования, способ неверного положения, способ секущих, способ Стеффенсена.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.
1.
Шикин Е. В., Чхартишвили А. Г.
Математические способы и модели в управлении: Учеб. пособие. – М.: Дело, 2000. – 440 с.
2.
Амосов А. А., Дубинский Ю. А., Копчёнова Н. В.
Вычислительные способы для инженеров: Учеб. пособие. – М.: Высш. Школа, 1994. – 544 с.
3.
Демидович Б. П., Марон И. А., Шувалова Э. З.
Численные способы анализа. 2-е изд., испр. и доп. – М.: Гос. изд-во физ .-мат. Лит., 1963. – 400 с.
]]>

