Учебная работа. Реферат: Расчет плоских ферм при подвижной нагрузке
Сургутский государственный Педагогический Институт
Кафедра высшей математики.
Реферат
«методы расчета ферм при подвижной нагрузке»
по дисциплине: простейшие динамические модели.
Выполнил:
студентка Факультет ДНиМО, 4 курс
Макарова елена Вячеславовна
Проверил:
профессор Кащеев В. П.
Сургут, 2001 год.
Оглавление
Введение. 2
Глава 1. Расчет плоских ферм. 3
§1 метод вырезания узлов. 4
§2 Определение усилий в стержнях фермы построением диаграммы Максвелла-Кремоны. 5
§3 Определение усилий в стержнях фермы методом сечений (методом Риттера). 7
Глава 2.Расчет плоской фермы на подвижную нагрузку.
8
Заключение. 12
Литература. 13
Введение
такая конструкция как плоская ферма, используется очень часто в строительстве, в проектировании. Любая ферма, и ее стержни, как составляющие, несет на себе некую нагрузку. Как правило, нагрузка на ферму – подвижна (примером тому можно привести фермы мостов). Расчет необходимой прочности стержней мостов, расчет усилий для каждого стержня при заданной нагрузке, в этом случае, один из важнейших элементов подготовки к строительству.
Для раскрытия темы реферата потребуется теоретический материал, а также иллюстрация его практического применения. В необходимое теоретическое обоснование решения представленной задачи входят описание основных теоретических методов расчета плоских ферм на нагрузку.
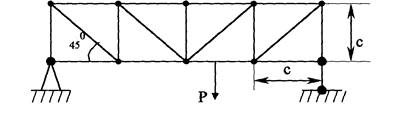
Практическая часть работы представлена решением следующей задачи: рассчитать на прочность (т. е. подобрать площадь сечения) стержни 1, 2, 3, определив предварительно опасное положение силы Р=50 тонн, движущейся по нижнему поясу фермы; нагрузка, при движении груза, передается только на узлы фермы. Принять допустимое напряжение
s = 7600 кг/см2
.
Решение поставленной задачи позволяет рассчитать линейные размеры конструкции при определенных начальных условиях, таких как максимальная нагрузка и допустимое для материала, из которого изготовлена конструкция.
Глава 1. Расчет плоских ферм
Фермой
называется жесткая (геометрически неизменяемая) конструкция из прямолинейных стержней, соединенных на концах шарнирами (рис. 1).
Ферму называют плоской,
если все ее стержни лежат в одной плоскости. Метод соединения стержней фермы называют узлами.
Все внешние нагрузки к ферме прикладываются только в узлах. При расчете фермы, трением в узлах и весом стержней (по сравнению с внешними нагрузками), пренебрегают или распределяют веса стержней по узлам, тогда на каждый из стержней фермы будут действовать две силы, приложенные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или сжатие.
Ферма считается статически определимой, если число узлов n и число стержней m удовлетворяют уравнению:
m=2n-3 если число стержней не удовлетворяет этому равенству, то возможны два случая:
1. если: m>2n-3,
ферма является в этом случае статически неопределимой;
2. если: m<2n-3,
то конструкция перестает быть геометрически неизменяемой. Получает подвижность, следовательно, становится механизмом.
Расчет фермы сводится к определению опорных реакций и усилий в ее стержнях. Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело. Расчет усилий в стержнях фермы методами статики может быть произведен только для статически определимых ферм.
§1 метод вырезания узлов.
Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов, определению усилий в стержнях фермы.
Активные силы и реакции опор являются внешними силами для всей фермы, рассматриваемой как твердое тело; усилия в стержнях в этом случае — внутренние силы. поэтому для определения усилий необходимо рассмотреть равновесие части фермы, для которой искомые усилия являются внешними силами.
При решении задач на расчете ферм способом вырезания узлов необходимо придерживаться следующего плана действий:
1. Выбор тела (или т ел),равновесие которого должно быть рассмотрено. Для решения задачи надо рассмотреть равновесие тела, к которому приложены заданные и искомые силы или силы, равные искомым (например, если надо найти давление на опору, то можно рассмотреть равновесие тела, к которому приложена численно равная этой силе реакция опоры и т. п.).
2. Когда заданные силы действуют на одно тело, а искомые на другое или когда те и другие силы действуют одновременно на несколько тел, может оказаться необходимым рассмотреть равновесие системы этих тел или последовательно равновесие каждого тела в отдельности.
3. Изображение действующих (активных) сил. Установив равновесие какого тела или тел рассматривается (и только после этого), следует на чертеже изобразить все действующие на это тело, (или тела) внешние силы, включая как заданные, таи и искомые сковы, в том числе реакции всех связей.
4. Составление условий равновесия. Условия равновесия составляют для сил, действующих на тело (или тела), равновесие которых рассматривается.
5. Определение ,реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматриваемой как твердое тело, проверка правильности решения и исследование полученных результатов.
6. Вырезать узел, в котором сходятся два стержня, и рассмотреть его равновесие под действием активных сил и реакций разрезанных стержней; определить эти реакции
7. Переходя от узла к узлу, рассматривать аналогично равновесие каждого узла.
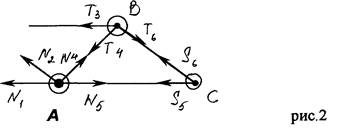
§2 Определение усилий в стержнях фермы построением диаграммы Максвелла-Кремоны.
Это графический способ расчета усилий в стержнях фермы. Построение диаграммы Максвелла-Кремоны заключается в построении силовых многоугольников, построенных для всех узлов фермы, в один чертеж так, чтобы ни одно из усилий не повторялось дважды (рис. 3).
При расчете фермы способом Максвелла-Кремоны следует придерживаться следующей последовательности действий:
Определить реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматриваемой как твердое тело.
Отбросить опоры и изобразить все приложенные к ферме внешние силы, включая реакции опор, так чтобы эти векторы располагались вне контура фермы.
части плоскости, ограниченные контуром фермы и линиями действия внешних сил, а так же те, что ограниченны стержнями фермы, обозначить буквами; узлы обозначить римскими цифрами, стержни — нумеруем арабскими.
построить замкнутый многоугольник внешних сил, откладывая силы в том порядке, в котором они встречаются при обходе фермы (направление произвольно) силы обозначаются малыми буквами, соответствующими обозначениям смежных участков плоскости.
последовательно, на том же рисунке, построить силовые многоугольники для каждого узла (узлы выбираются таким образом, чтобы число неизвестных усилий в стержнях равнялось двум), направление обхода узла должно совпадать с направлением обхода плоскости.
Стержень считать сжатым, если направление, указанное известными силами, направлено к узлу, в противном случае стержень растянут
Измерить на диаграмме отрезки, изображающие искомые усилия в стержнях фермы, и найти усилия, учитывая принятый масштаб сил.
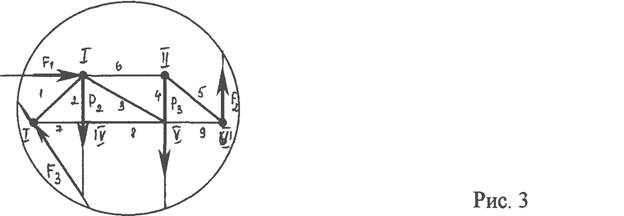
§3 Определение усилий в стержнях фермы методом сечений (методом Риттера).
Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, например, для проверочных расчетов (рис. 4)
При расчете методом сечении рекомендуется такая последовательность действии:
1. определить реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматриваемой как твердое тело, находящееся под действием плоской системы сил.
2. Ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е., считая их растянутыми.
3. затем составляются уравнения равновесия так, чтобы в каждое уравнение входило одно неизвестное усилие.
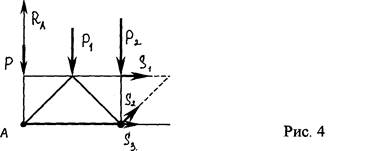
4. Из полученных уравнений находятся неизвестные усилия в стержнях; если в ответе получается знак «-», то это означает, что стержень сжат, а не растянут.
Глава 2.Расчет плоской фермы на подвижную нагрузку.
Содержание главы представляет из себя решение задачи на расчет плоской фермы при подвижной нагрузке.
Задача:
Рассчитать на прочность (т. е. подобрать площадь сечения) стержни 1, 2, 3, определив предварительно опасное положение силы Р=50 тонн, движущейся по нижнему поясу фермы; нагрузка , при движении груза, передается только на узлы фермы. Принять допустимое напряжение сигма
= 1600
кг/см2
.
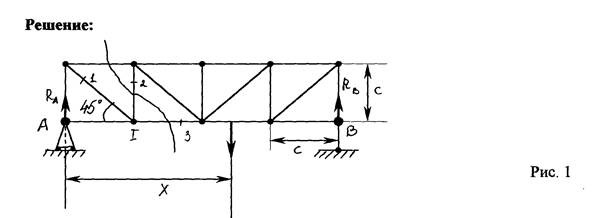
Для определения усилий в стержнях сначала необходимо найти реакции опор А и В. Для этого мысленно отбросим опоры и заменим их действие на ферму реакциями ra
и rb
. Составим условия равновесия:
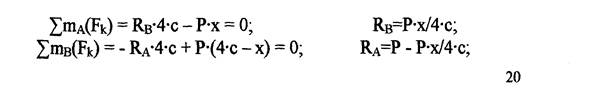
0<=х=>4с
Проверим правильность полученных реакций:
åFky
=RA
+RB
-P=0, 0=0
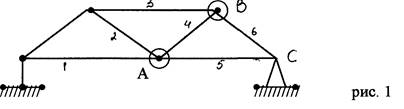
Проведем сечение конструкции так, как указано на рис.1, и рассмотрим равновесие левой части фермы (рис.2), заменяя действие на нее правой части силами, направленными вдоль стержней (соответственно N0
, N2
, N3
) . Составим условия равновесия, учитывая, что нагрузка движется слева направо, а «х» есть изменение расстояние от опоры до узла, в котором приложена сила. Найдем усилия в стержнях для случая, когда 0<=х=>с
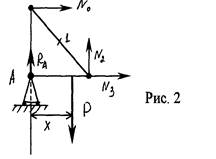
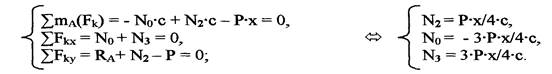
Рассмотрим теперь случай, когда 2с<=х=>4с (рис. 3). Так как нагрузка передается только на узлы, то условия равновесия будут иметь следующий вид:
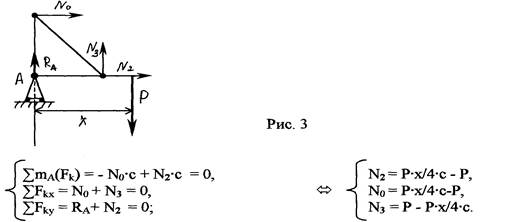
Таким образом, найдены усилия в стержнях 2 и 3. Для того, чтобы найти усилие в стержне 1 , применим метод вырезания узлов. Вырежем узел I. (Рис. 4) Составим условия равновесия, учитывая, что 0<=х=>с.
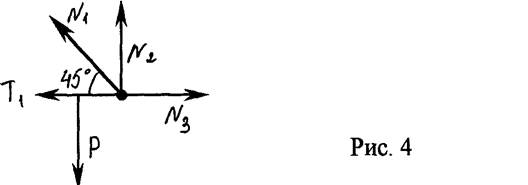
åFky
= N2
+N1*
cos(45°) — P = 0; Û N1
= (P – Px/ 4c)Ö2
Составим условия равновесия, учитывая, что 2с<=х=>4с.
åFky
= N2
+N1*
cos(45°) = 0; Û N1
= (P – Px/ 4c)Ö2
Можно сделать вывод, что усилие в стержне 1 не зависит от точки приложения груза. Изобразим наглядно изменения усилий в стержнях при подвижной нагрузке.
Для стержня 1:
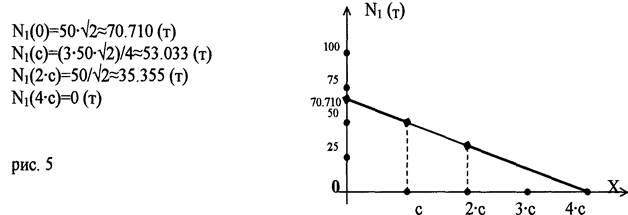
Из графиков легко можно определить наиболее опасные положения груза для каждого из рассматриваемых стержней, а, следовательно, и определить оптимальные площади сечений для них.
Площадь сечения (обозначим ее буквой S) элемента конструкции должна быть больше или равна отношению усилия, прилагаемого к этому элементу, к допустимому напряжению.
Для стержня 1:
наиболее опасно положение груза при х= 0, тогда абсолютное
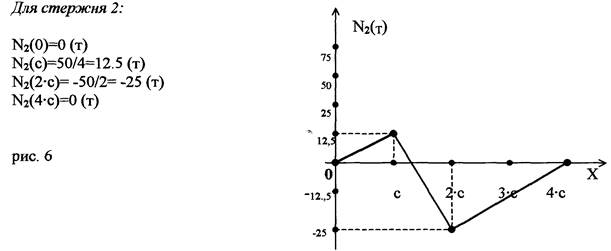
Для стержня 2:
наиболее опасно положение груза при х= 2с, тогда абсолютное
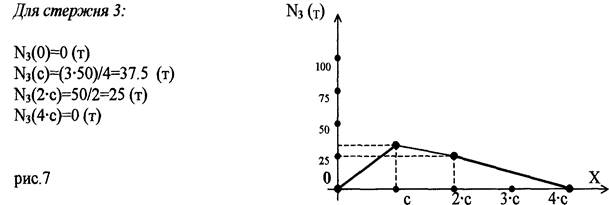
Для стержня 3:
наиболее опасно положение груза при х= с, тогда абсолютное
таким образом, можно сделать вывод, что стержень 1 подвергается наибольшему воздействию, из трех исследуемых стержней. задача решена. Заключение.
В своей курсовой работе я рассмотрела одну из областей применения методов математики на теоретическом и практическом материале. В теоретическое обоснование решения математической задачи, поставленной темой курсовой, вошли: основные понятия статики, исходные положения статики, теория о связях и их реакциях, теория о системах сил (сходящихся и плоских), а также методы расчета плоских ферм. итог курсовой работы — применение изложенной теории к решению конкретной задачи. Литература
1. Б а т ь М. И., Джанелидзе Г. Ю., КельзонА. С. Теоретическая механика в примерах и задачах: 2. Т а р г С. М. краткий курс теоретической механики:
Учеб. пособие для втузов. Т. 1. — М.: Наука. Гл. ред. физ.-мат.. лит., 1990.
Учебник для втузов. 12-е издание, — М.: Высшая школа, 1998.

