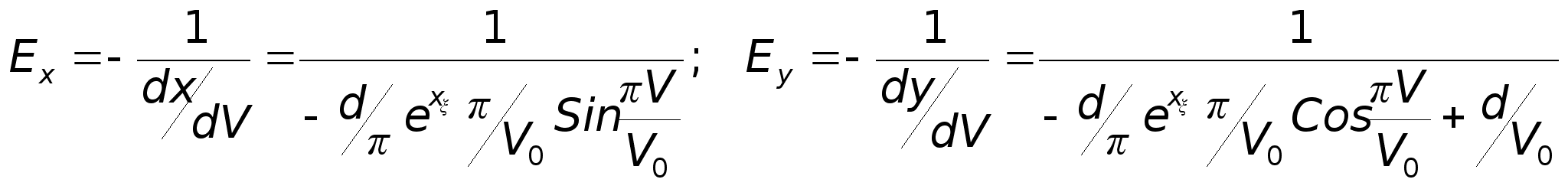Учебная работа. Реферат: Техника и электроника СВЧ (Часть 1)
1
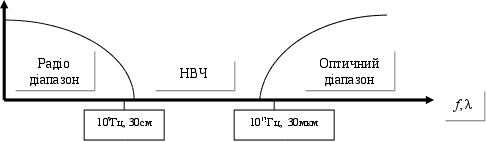
Існують
локаційні
пристрої, які
повинні працювати
на ~мм,
~100ГГц.
Оскільки
~1м мають
малу роздільну
здатність, а
оптичний діапазон
швидко поглинаються
постає необхідність
вивчення НВЧ
діапазону.
Перші НВЧ
прилади виникли
під час 2-ї світової
війни при створенні
РЛС. Застосування
НВЧ електроніки:
Малопотужна
електроніка:
НВЧ телебачення
– супутникове,
мобільні телефони,
комп’ютери.
Потужна
електроніка:
НВЧ — піч, РЛ –
електроніка.
Фізичні
причини виділення
діапазону НВЧ
D –
розмір об’єкта.
При
 —
—
закон Кірхгофа,
Ома,
 —
—
використовуються
закони променевої
оптики,

— НВЧ діапазон,
диференційна
інтерференція.
Отже в НВЧ не
можемо користуватись
законами Кірхгофа
і геометричної
оптики. Закони
Кірхгофа мають
місце до якихось
частот та швидкості
розповсюдження
інформації
– швидкості
світла.
Р озглянемо
озглянемо
малюнок. Даний
ланцюг можна
розрахувати
за допомогою
закону Ома,
поки генератор
– постійного
струму. Розглянемо
змінну напругу:
електрон почне
рух тоді, коли
сигнал про
потенціал дійде
до нього:
 .
.
Якщо частота
генератора
така, що
 ,
,
то в той час,
як електрон
рухається в
одну сторону,
генератор вже
сформував
зворотній
потенціал,
тобто існують
струми в різних
напрямках. Отже
не можна використовувати
звичайні закони.
Описаний
ефект – ефект
запізнення.

на частоті

при таких
 працюють
працюють
РЛС. На частоті
10ГГц
при
 ніяких
ніяких
законів Кірхгофа,
Ома вже застосовувати
не можна.
Виникнення
випромінювання.
При змінному
струмі можливе
випромінювання,
на його характеристики
впливає відстань
між дротами
по відношенню
до
 .
.
50Гц: ~100км.
Тому зі збільшенням
частоти основна
енергія знаходиться
поза провідником
у вигляді поля.
При високій
частоті – густина
струму розподілена
нерівномірно,
електрони
рухаються в
скін шарі товщиною
~1мкм.
Тому опір потрібно
рахувати іншими
законами.
Найбільш
розвинутий
оптичний
діапазон НВЧ.
Рівняння
Максвела 2-ого
порядку описують
всі електромагнітні
явища:
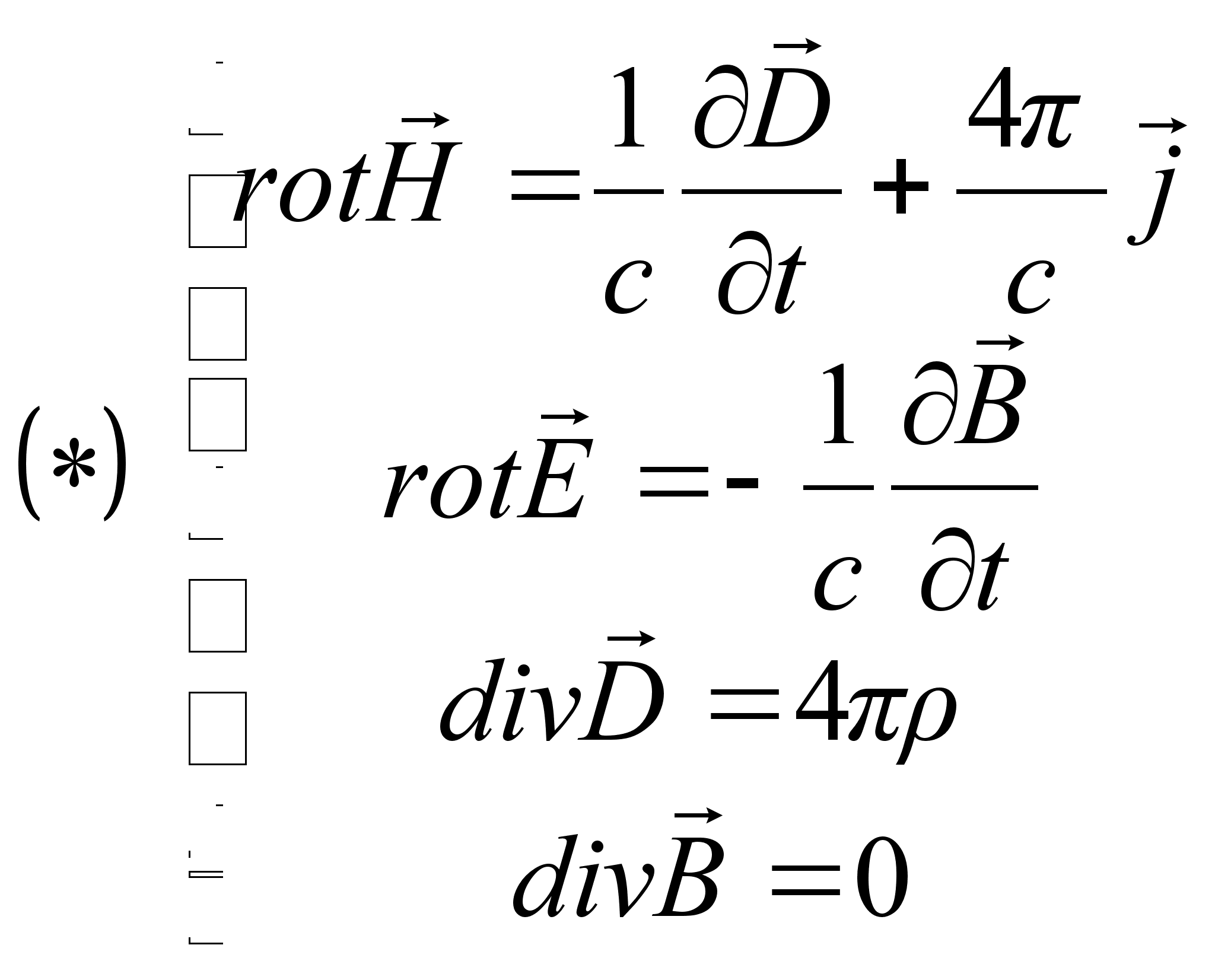
де
 —
—
густина струму,
 —
—
напруженість
ЕП,
 —
—
напруженість
МП,
 —
—
індукція МП,
 —
—
індукція ЕП,
 —
—
густина заряду,
 —
—
поверхневий
струм.
Поки що монополь
Дірака не виявлено.
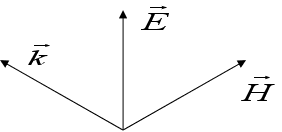
Знаки
розставлено
відповідно
до положення
векторів
 ,
,

та напрямку
розповсюдження
хвилі
 —
—
утворюють праву
трійку. Це – не
всі рівняння
Максвела, у
такій формі
їх іноді називають
рівняннями
Герца.
Рівняння
записано в
СГСЕ. В системі
СІ не буде
 ,
,
 —
—
це зручно, але
в СІ опір вільного
простору скінчений,
що немає фізичного
змісту.
Ці диференційні
рівняння в
частинних
похідних другого
порядку неоднорідні.
Хоча з точки
зору математики
рівняння Максвела
лінійні. Але
лінійні рівняння
ніколи не описують
підсилення,
генерації і
т.д. Електромагнітні
процеси нелінійні.
Нелінійність
обумовлюється
речовиною, яку
описують рівняння:
 .
.
Народження
електрону —
позитивної
пари в вакуумі
– нелінійний
процес. Крім
цього можна
генерувати
гармоніки, 1 з
1050
фотонів зливаються
і дають новий
фотон.
 ,
,
 (А/см2),
(А/см2),
поверхневий
струм —
 ,
,
 (А/см).
(А/см).
Матеріальне
рівняння –
рівняння
неперервності.
 .
.
Ніякого струму
не може бути
якщо заряд не
виноситься.
 —
—
що виноситься
 —
—
що залишається
в середині.
 —
—
це рівняння
в частинних
похідних, тому
дуже важливі
граничні та
початкові
умови. Всі фізичні
поля неперервні
з точки зору
фізики.
Граничні
умови:
 ,
,
 .
.
Магнітне
поле всередині
металу(має
уявні розриви):
 .
.
Не буває
нульової товщини
тому всередині
металу буде
плавний перехід,
тому що поля
неперервні.
В векторному
вигляді:
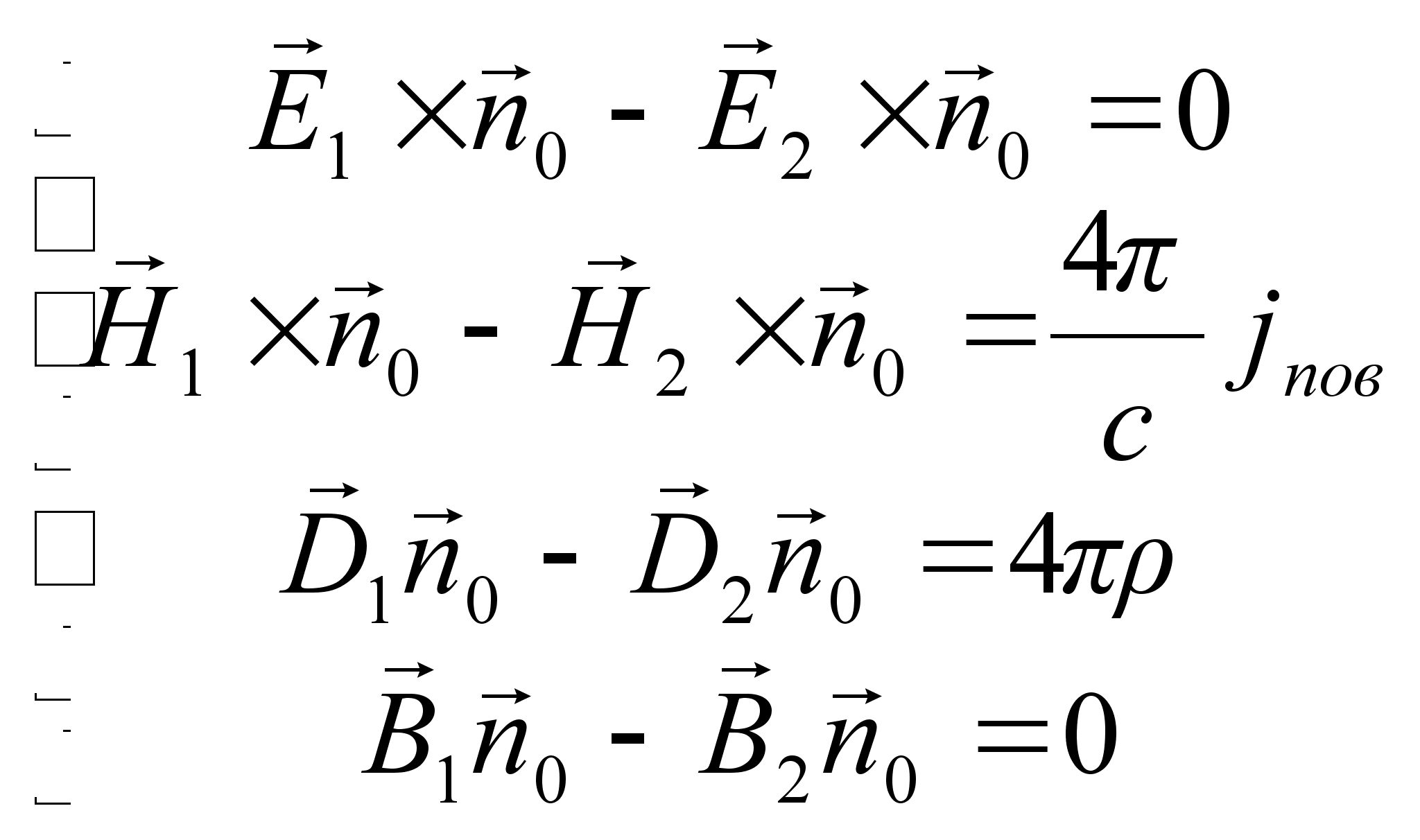
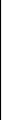

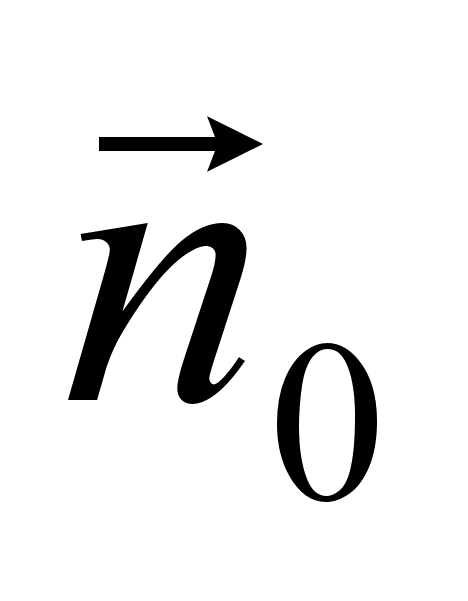
(1)
(2)
Якщо змінимо
граничні умови,
то все повністю
змінюється.
 —
—
права трійка.
Тому знак “-“
в
 .
.
У рівняннях
в комплексній
формі цього
немає. Мінус
там може бути
в 1-му і 2-му рівнянні
в системі (*).
Граничні
умови в металі:
 .
.
Гранична
умова в ідеальному
металі:

(для нетензорного
середовища).
 —
—
для
 металу.
металу.
Якщо присутнє
 ,
,
то за рахунок
сили Лоренца
виникає струм.
Для напівпровідника:
У застосуванні
граничних умов
головне те, що
ми не розв’язуємо
рівняння в
середині матеріалу,
а розв’язуємо
рівняння лише
на поверхні.
Лекція
10
Реальний
смушковий
несиметричний
хвильовід.
У попередній
задачі ми нехтували
всіма розмірами
– розглядали
ідеальний
випадок. Тепер
розглянемо
реальний:
скористаємося
тими самими
моделями: нехай
розповсюджується
Т – хвиля, а ми
розглядаємо
одну половину
(симетрія).
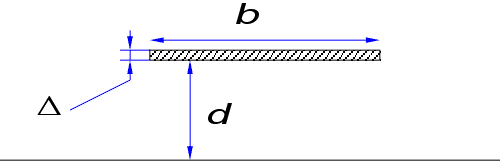
Використаємо
конформні
відображення:
 .
.
тут
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
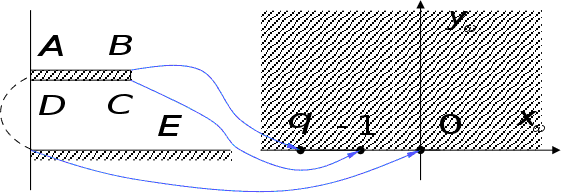
Точка

визначається
обраним масштабом;
ми знайдемо
її потім з граничних
умов. Таким
чином ми маємо:
 .
.
Проінтегрувавши,
маємо:
 .
.
Лінія
з втратами
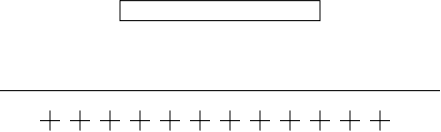
Нехай
існують лише
втрати в металі.
Для їх розрахунку
потрібно знайти
струм
 .
.
Для цього можна
використати
вектор Умова-Пойтінга.
Треба розрахувати
потік енергії
з лінії в метал.
Знайдемо частину
 :
:
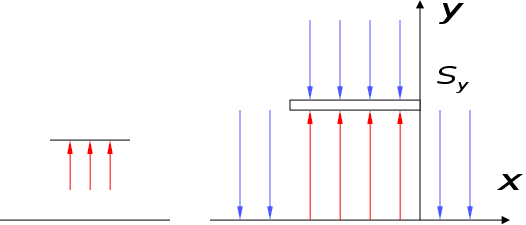
 .
.
Оскільки ми
розглядаємо
Т – хвилю, то
 ;
;
тому втрат
енергії немає
(це для ідеальної
хвилі). Щоб наблизити
задачу до реальної,
потрібно використати
граничні умови
Леонтовича:
 .
.
Тоді все рівно

але друга складова
зберігається:
 .
.
Підставивши,
одержимо:
 ,
,
тут
 —
—
середовище
куди іде хвиля.
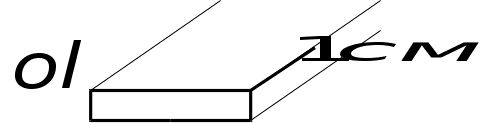
Тепер
знайдемо повну
потужність,
що входить у
метал: це
 ,
,
але можна розрахувати
на одиницю
довжини хвильовода.
Для цього розрахуємо

по контуру
 ,
,
і це буде потужність
на 1 см.
 .
.
Тоді втрати
характеризуються
 —
—
потужність,
що розповсюджується
в лінії. Вона
зменшується
з відстанню:
 .
.
стала
затухання:
 .
.
М и
и
знаємо
 ,
,
знайдемо
 .
.
Для цього запишемо
вектор Умова-Пойтінга
для хвилі, що
розповсюджується
в хвилеводі:
 .
.
Ця хвиля розповсюджується
по всій площині
 ,
,
тому
 .
.
Ми одержали
в (*) знак “-“. Однак
ми не будемо
ставити його
(оскільки при
зміні напрямку
знак змінюється,
то вважатимемо
просто

завдяки симетрії
задачі). таким
чином:
 .
.
Оцінимо цю
величину:
Введемо
наближення:
будемо враховувати
поле лише у
заштрихованій
ділянці, оскільки
тут більша
частина (тому,
що ця потужність
зумовлена
ємністю, а вона
сконцентрована
в цій ділянці).

— характеризує
якість лінії,
але частіше
використовують
добротність
лінії:
 ,
,
де

(по аналогії
з добротністю
КК:
 ).
).
Для
Хвильоводів
—
 ;
;
Коаксіальних
кабелів —
 ;
;
Мікросмушкових
ліній —
 .
.
Оцінимо
довжину хвильовода,
в якому хвиля
затухає в

разів при
 :
:
 .
.
Крім втрат у
металі, існують
і інші механізми
– для них теж
можна обчислити
 ,
,
яке додається
до нашого. Наприклад,
це витрати на
випромінювання
(радіаційні):
 .
.
Де
 —
—
опір лінії.
Існують також
діелектричні
втрати (розглянемо
нижче); найкращий
діелектрик
– тефлон.
Розглянемо
хвильовий опір
лінії:
 ;
;
або
 ,
,
де С – ємність
лінії. Обчисливши
її, одержимо:
 [Ом].
[Ом].
Лекція
11
С
 иметрична
иметричнасмушкова хвильовід.
Скористаємося
тими самими
наближеннями:
Т
– хвиля;

рівняння Лапласа

конформні
відображення.
Розглянемо
половину (симетрія).
Застосуємо
перетворення
Кристофеля-Шварца.
Далі – аналогічно
попереднім
задачам. Розв’язавши,
одержимо картинку
полів:
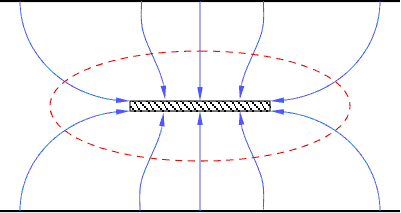
Її параметри:
 .
.
тут

менше, аніж у
попередній
лінії, оскільки
ємність тут
більша. Однак,
тут

менше не в 2 рази,
оскільки у
попередньому
хвильоводі
ємність враховувалась
і до верхньої
сторони верхньої
смужки, і до
нижньої (див.
Мал.), тому там
ємність більша,
аніж у звичайному
конденсаторі.
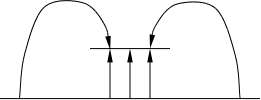
Довжина
хвилі для симетрично
смушкової лінії
 ,
,
якщо всі три
смушки знаходяться
в середовищі
 .
.
В
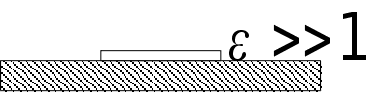 ідкриті
ідкритілінії.
тут смужка
на шарі діелектрику.
Тоді:
Зверху
—
 .
.
Знизу
—
 .
.
Тому
використовують
деяке ефективне
 :
:
 ,
,
треба знайти
частину енергії,
яка йде по
діелектрику.
Нехай ця частина

в
 .
.
Тоді:
 .
.
часто використовують
таку наближену
формулу:
 .
.
Лекція
12
Повільні
хвилі.
Для багатьох
електричних
приладів необхідно
отримати хвилю,
що рухається
зі швидкістю
 .
.
Це зокрема
стосується
приладів, у
яких відбувається
передача енергії
та інформації
від хвилі іншим
носіям. Однак,
згідно Ейнштейну,
хвилі у вакуумі
рухаються зі
швидкістю
світла, а будь-який
інший носій
(наприклад
 )
)
не може рухатися
зі швидкістю
 .
.
Д ля
ля
створення
уповільнених
хвиль використовуються
різні спеціальні
хвильоводи:
Передача
енергії від
електричного
потоку до ЕМ
– поля називається
ефектом Вавілова-Черенкова.
Він виникає,
коли швидкості
електричного
потоку та ЕМ
– хвилі рівні.
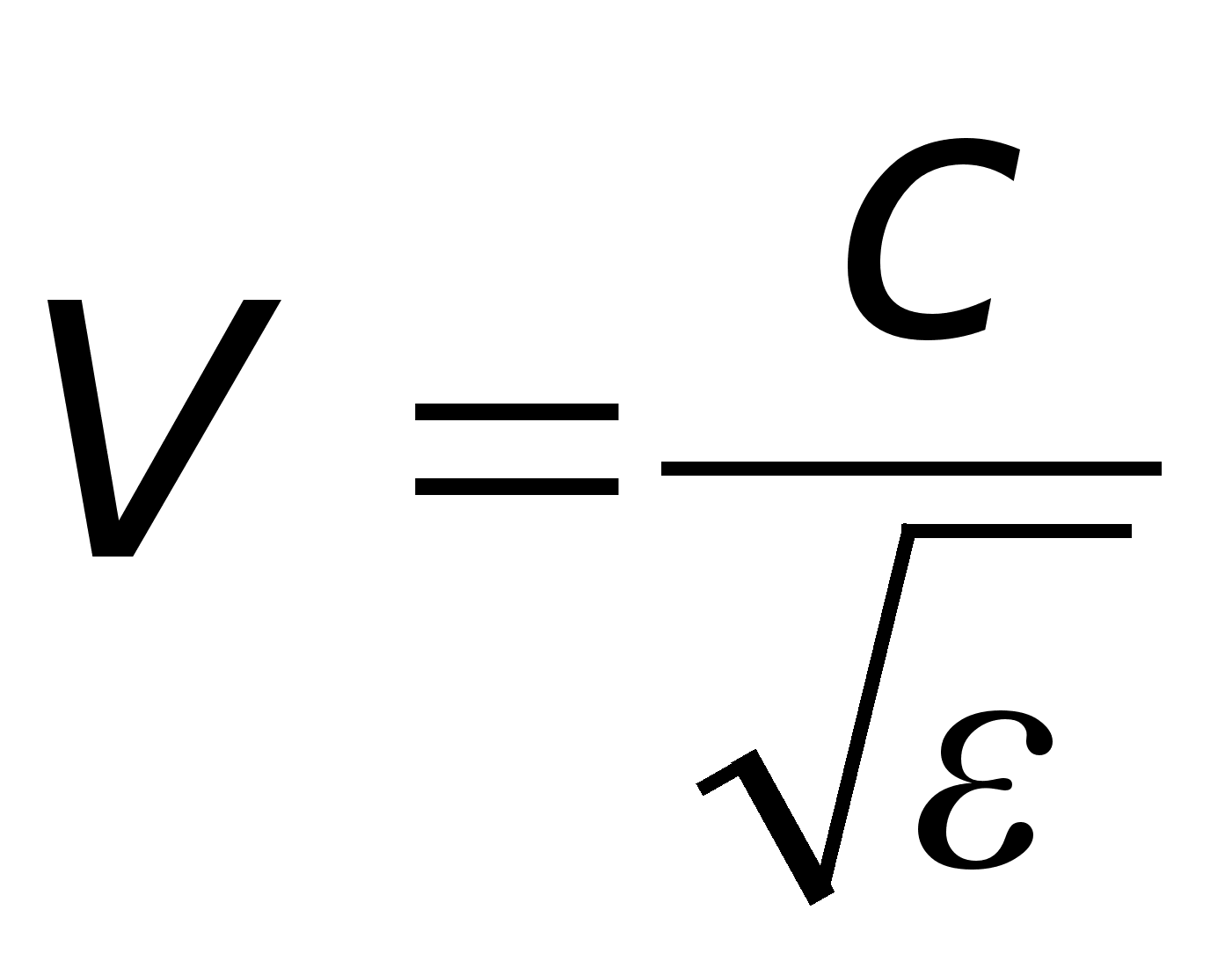
 .
.
метод передачі
енергії: в
діелектрику
– вузький канал,
куди запускають
потік електронів.
метод уповільнення:
використовуються
дифракційні
ефекти.
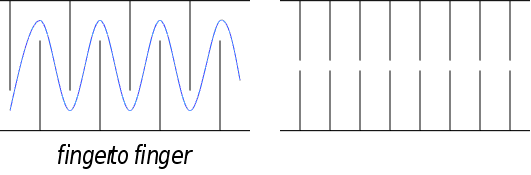
Розглянемо
прямокутний
хвильовід з
діелектрику:

Розповсюдження
хвилі в бруску
з діелектриком
– за рахунок
повного відбиття.
Це – відкриті
діелектричні
хвильоводи
(бо немає металевих
стінок) або
світловоди.
На практиці
використовуються
круглі волокна
(див. мал.) – fiber-glass.

Досягнення
полягає в тому,
що немає металу,
яким обумовлена
більшість
втрат. Ця лінія
також є уповільнюючою,
бо:
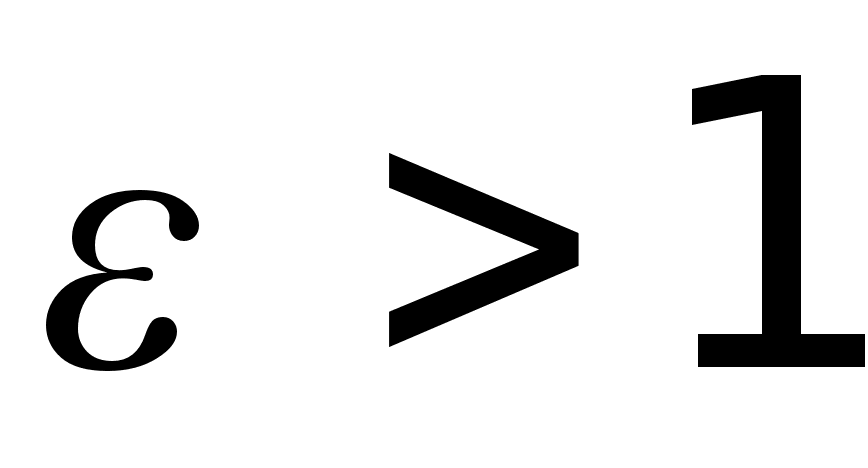
непрямолінійне
розповсюдження
хвилі,
 .
.
Хвиля існує
не лише в хвильоводі,
але й в металі,
бо хвильовід
– відкритий.
Висновки
Ейнштейна про
те, що фотон у
вакуумі рухається
зі швидкістю
 ,
,
стосується
вільного
нескінченного
простору, тому
за межами хвильовода
неподалік від
нього поле є,
і воно рухається
зі швидкістю
 ;
;
проте на

поля бути не
може через
експоненційне
спадання поля.
З інших
міркувань:
хвиля не виходить
з діелектрику,
тому, що всередині
швидкість

тобто імпульс
 ;
;
і згідно з законом
збереження
імпульсу хвиля
не може вийти
з хвильоводу,
бо за його межами
імпульс має
бути
 .
.
Єдина умова
виходу хвилі
з хвильоводу
– тоді, коли
швидкість хвилі
в хвильоводі
стане рівною
с (імпульси
всередині і
зовні – однакові).
Розрахуємо
поле у fiber-glass:
шукаємо хвилю
Е або ТМ.
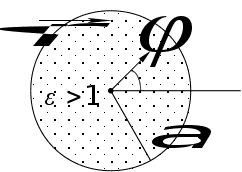
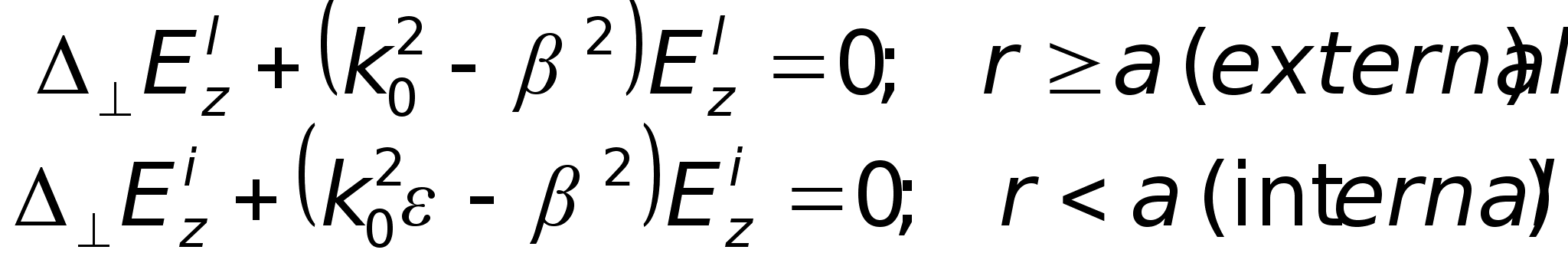
Розв’язки
обох рівнянь
(для зовнішнього
та внутрішнього
середовища)
необхідно
прирівняти
при

(на границі):
 ;
;
 .
.
В циліндричній
СК:
 .
.
Запишемо рівняння
для скалярної
функції:
 .
.
Розглянемо
симетричні
розв’язки:
 .
.
 .
.
 .
.
Якщо область
містить точку
 ;
;
то розв’язок
зручно брати
у вигляді функцій
Ханкеля, бо
саме в базисі

є функція, що
експоненційно
прямує до нуля
при
 .
.

— йде в

з хвильовода,
 —
—
йде з

в хвильовід.
Отже,
розв’язок треба
брати у вигляді:
 ,
,
 ,
,
тобто
 .
.
Граничні
умови для похідних
 .
.
Врахуємо

для

або
 ;
;

циліндрична
функція. Тоді
 .
.
таким чином
з граничних
умов одержали:
 .
.
Це – лінійна
однорідна
система відносно
А та В. Вона має
розв’язок за
умови
 :
:
 .
.
 .
.
Розв’язок
позначається

(перший індекс
в
 —
—
нуль, бо брали
 ).
).
Знайдемо
сталу розповсюдження:
 ,
,
тоді одержуємо:
 .
.
тут також
існує критична
довжина хвилі,
яка відповідає
 :
:
 .
.
Однак існує
більш жорстка
умова – умова
того, щоб хвиля
не пішла з
хвильоводу:
 :
:
 .
.
Умовою визначення
критичної хвилі
у відкритих
системах є не
рівність сталої
розповсюдження
 ,
,
а більш жорстка
умова
 .
.
Це – умова
невитікання
хвилі з хвильоводу.
Фізично вона
є законом збереження
імпульсу (коли
імпульси зовні
і всередині
співпадають,
з’являється
можливість
для витікання
хвилі.
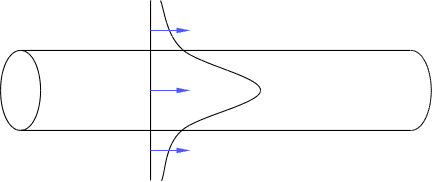
П риблизна
риблизна
картина розподілу

та

у хвильоводі
та зовні показана
на малюнку:
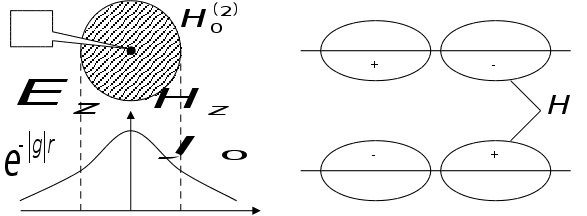
Ця картина
— для

( ,
,
1 – номер кореня).
Лекція
13
Гібридні
хвилі.
Раніше ми
розглядали
всі види хвиль
(Е, Н чи Т) окремо.
Однак у загальному
випадку хвиля
є суперпозицією
Е, Н, Т – повний
розв’язок
рівняння Максвела.
Гібридна
хвиля
– це хвиля, яка
має всі компоненти;
це суперпозиція
Е, Н, Т.
У випадку
розглянутому
вище, хвильовода
(стержня), ми
маємо три граничні
умови і дві
константи в
рівняннях, а
тому рівняння
в загальному
випадку не буде
мати розв’язків.
Однак, тут нам
потрібно розглядати
не тільки
 ,
,
 ,
,
 ,
,
а і хвилю
 :
:
 .
.
Тепер поле
описується
чотирма константами
і відповідно
чотирма граничними
умовами.
метод
узгодження
поперечного
імпедансу.
Гофра.

Покажемо,
що ця система
– уповільнююча.
Розглянемо
модель:
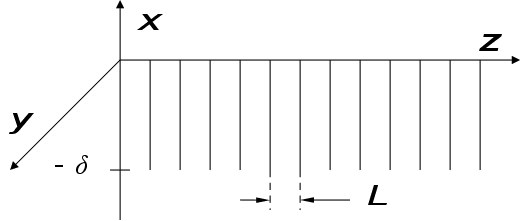
Уявимо,
що в цій системі
дійсно існує
хвиля, близька
до хвилі біля
круглого хвильоводу.
Нехай це буде
Е – хвиля, що
розповсюджується
в напрямку
 .
.
По аналогії
зі стержнем
 .
.
Виходячи з
цього, можна
знайти інші
компоненти:
 .
.
Це – компоненти
зовні. Що буде
всередині?
Всередині
будуть стоячі
хвилі:
 .
.
Це – дві Т — хвилі
(пряма і відбита).
Можна
розглянути
таке рішення
для

всередині:
 .
.
Тоді
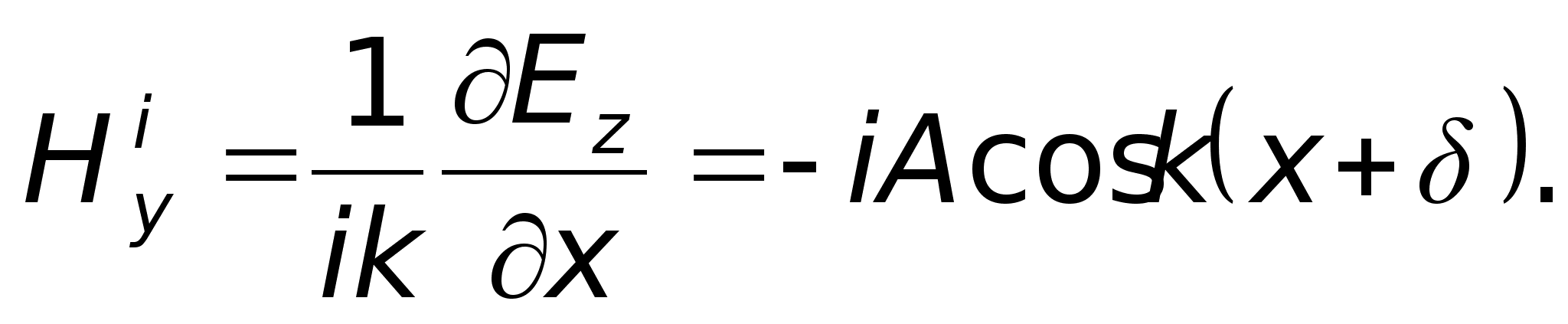
Пом’якшимо
умову (це метод
узгодження
поперечного
імпедансу) так,
щоб неперервні
були відношення
полів.
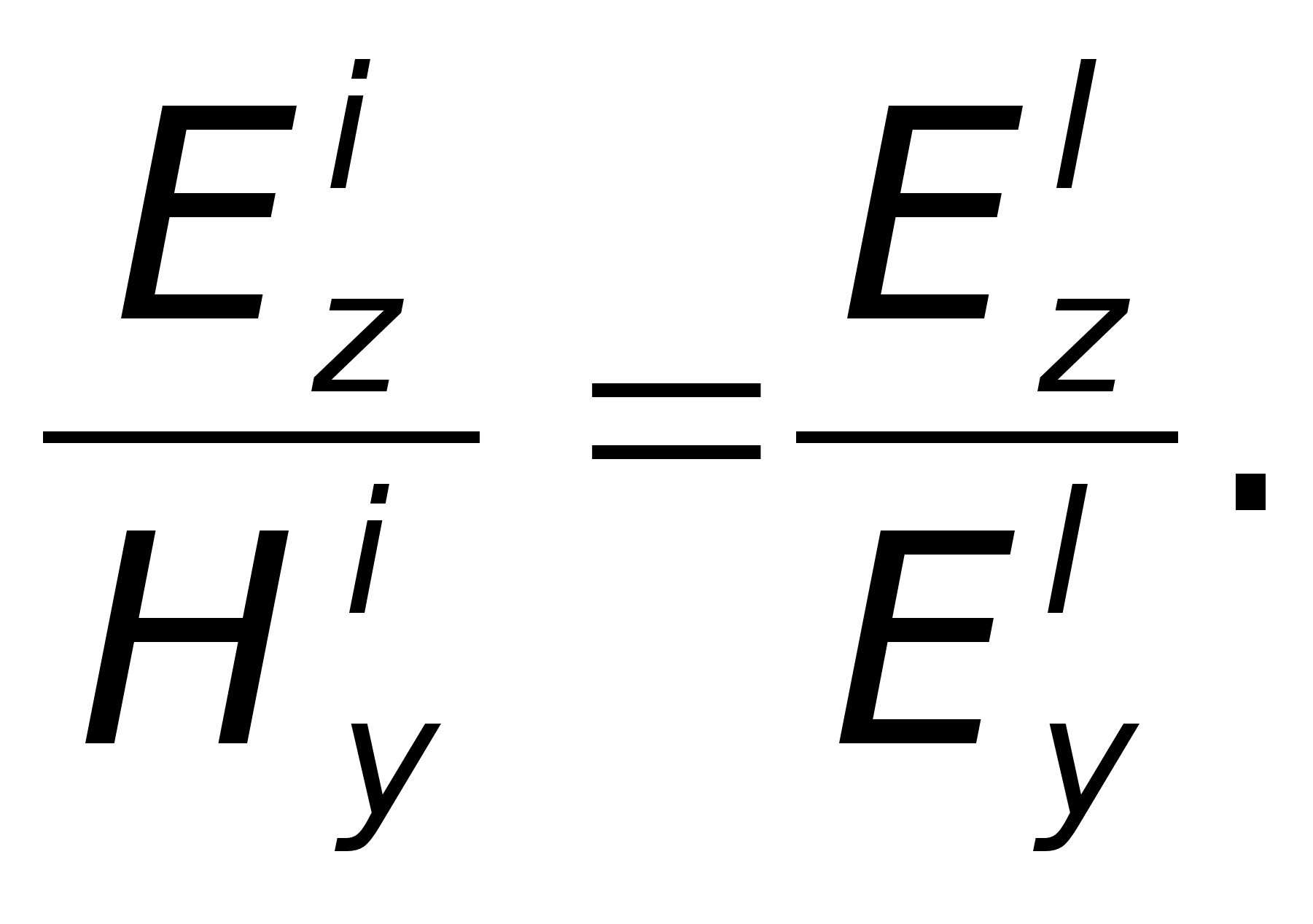
Тоді

.
Поперечна
стала розповсюдження
хвилі
 .
.
Т оді
оді
 .
.
 .
.
В точках

отримаємо
 .
.
Іноді будують
фотонну криву:
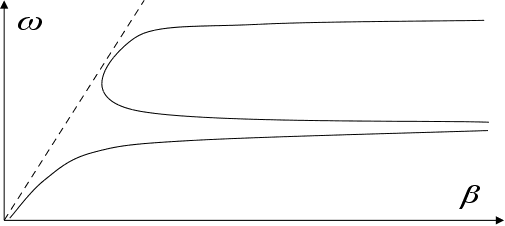
Маємо
ділянку, де
 ,
,
тобто маємо
уповільнення.
Це – звичайний
резонатор для
ЕМ – хвилі. При
розрахунках
у нас

переходило
в
 ,
,
а це можливо
при
 .
.
Це – ще одна
умова.
Спіраль.
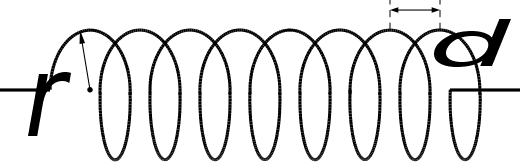
Тут
 ,
,
 .
.
Така система
по своїй конструкції
уповільнююча,
з коефіцієнтом
уповільнення
 .
.
Але тут теж є
резонансні
ефекти, що призводять
до уповільнення,
якщо
 .
.
Лекція
14
об’ємні
резонатори.
У них хвиля
“б’ється” між
стінками (див.
Мал.):
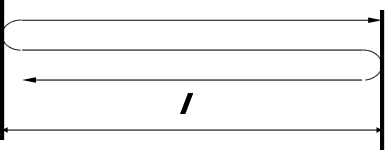
 ,
,
тоді хвиля, що
заходить у
резонатор, і
відбита, будуть
у фазі; тобто
це – умова резонансу.
Розв’яжемо
рівняння Максвела
для даної системи
– знайдемо
коливання, що
існують у цій
коробці.
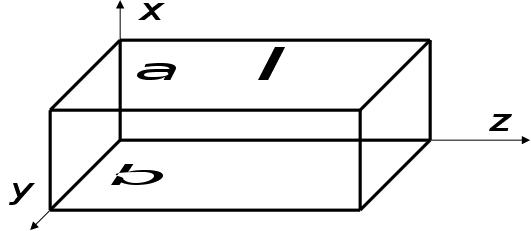
 .
.
З урахуванням
граничних умов
на бокових
стінках (стінках
хвильовода):
 .
.
Накладемо ще
дві граничні
умови:

звідки одержимо

— неправильно.
Це тому, що не
врахували
відбиття від
торців; правильно
буде записати:
 .
.
Тоді при накладанні
умови

одержимо
 .
.
 .
.
Розглянемо
 ,
,
одержимо
 .
.
Тоді
 .
.
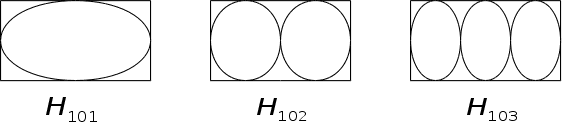
Типи коливань:
(останній індекс
– кількість
півхвиль)
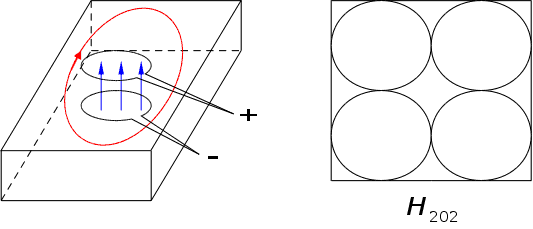
В круглому
резонаторі:
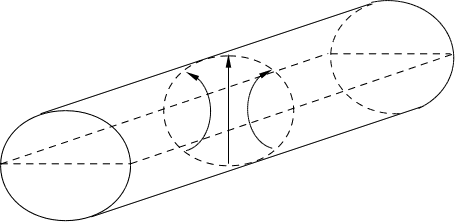
Існує дуже
багато типів
резонаторів.
Наприклад,
резонатор
хвилі, що біжить,
такий резонатор
ще називають
кільцевим.
Резонанс:
 .
.
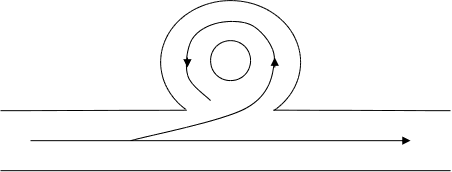
Добротність
резонаторів
 .
.
Для будь-якого
резонатора
звичайно існує
АЧХ, яка має
ширину.
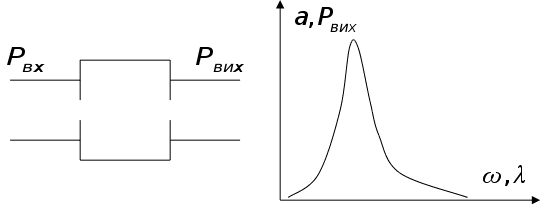
Напівширина

вимірюється
для

на 0.5; а для вихідної
амплітуди –
на 0.7 висоти
контуру.
 .
.
Хвиля затухає
із декрементом
 :
:
 ,
,
 .
.
Доведемо, що
 .
.
Це випливає
з розв’язку
рівняння:
 .
.
Втрати

— тут добротність
 .
.
Втрати можуть
бути в металі,
на випромінювання
в діелектрику:
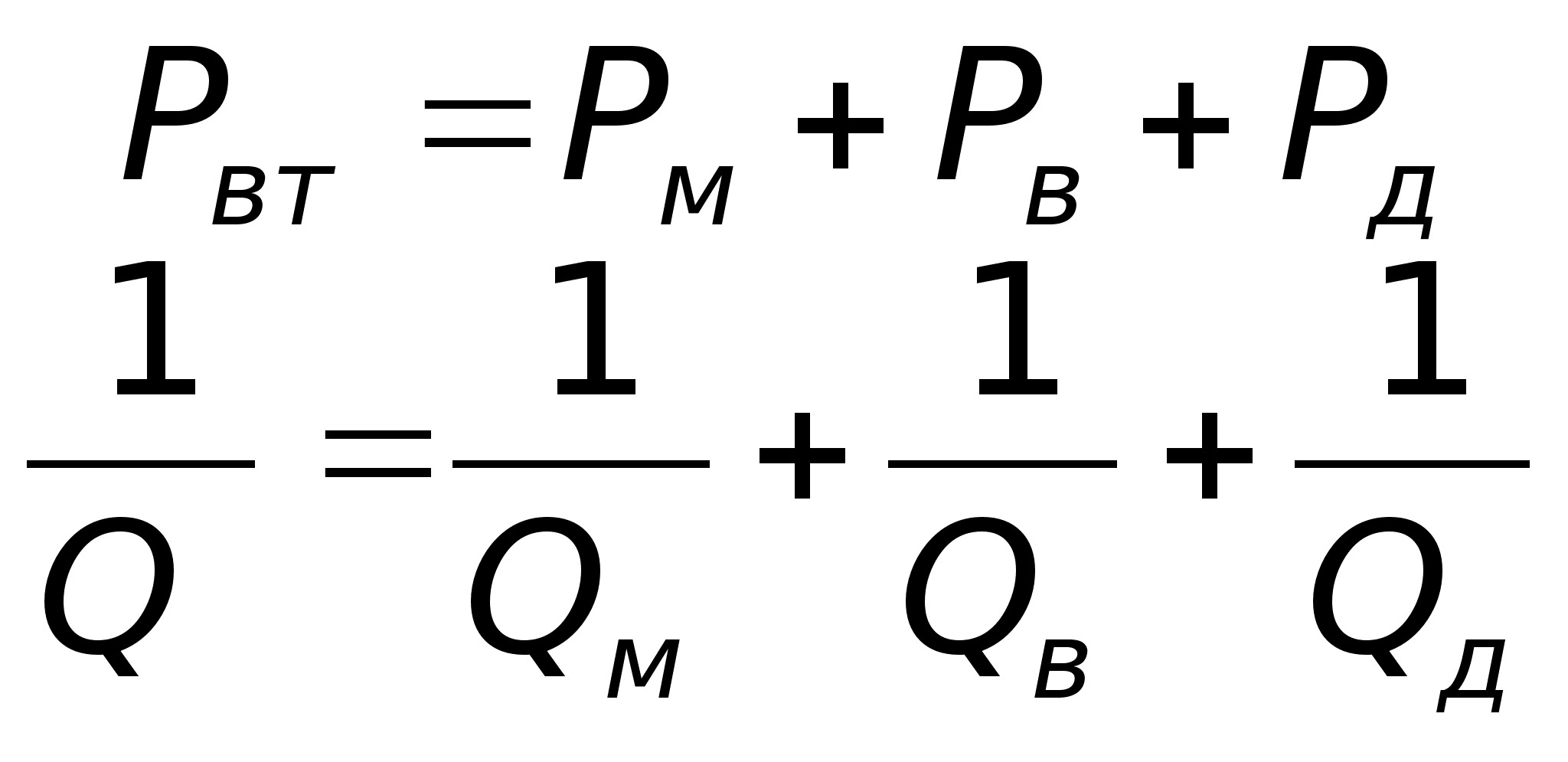
Підрахуємо
добротність,
пов’язану з
втратами у
діелектрику:
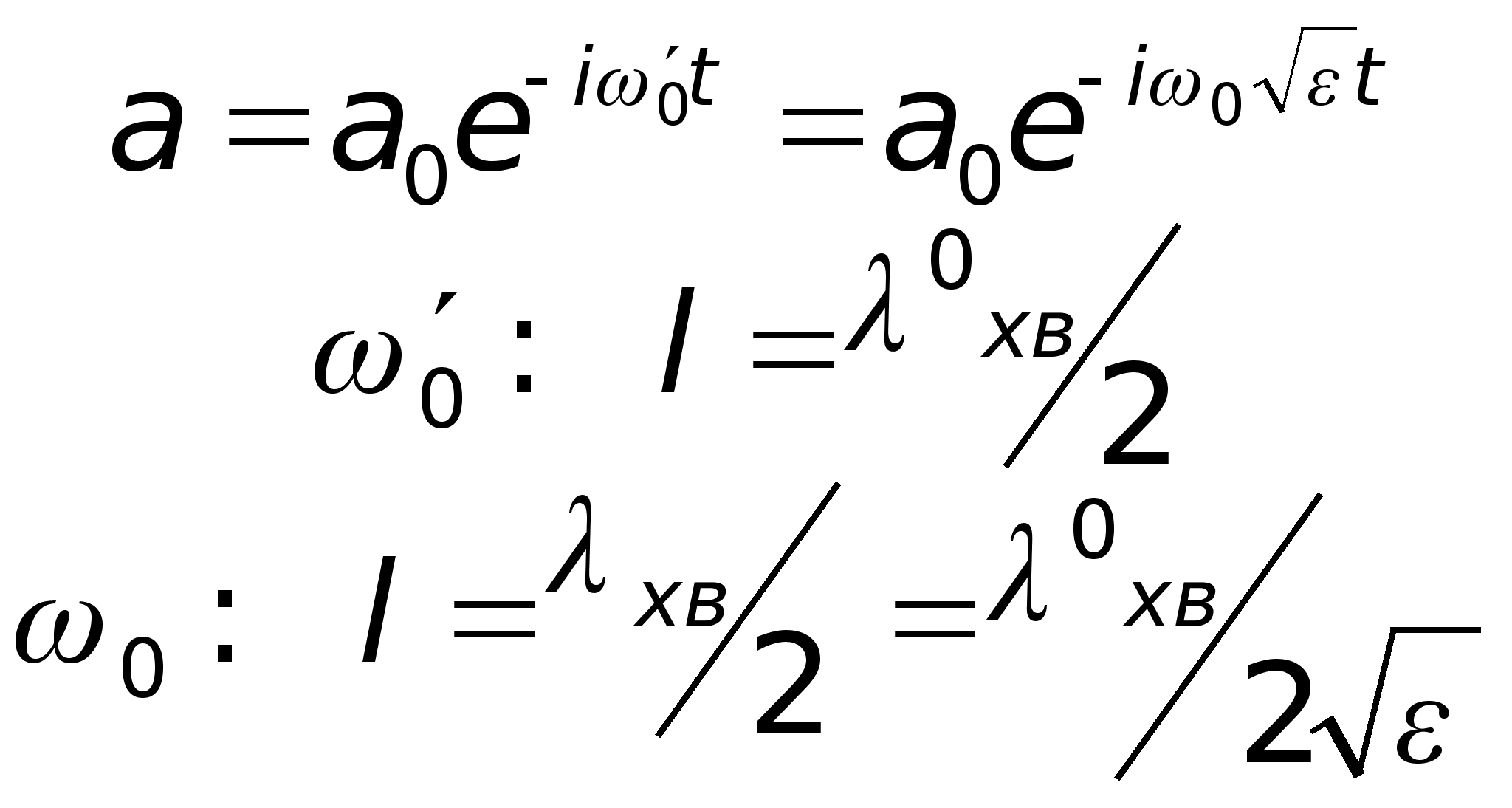
таким чином,

(
— коливання
резонатора
з діелектриком,

— порожнього)
.
 ,
,
де
 ,
,
отже
 .
.
таким чином
ми одержали
 ,
,
 .
.
Для розрахунку

в металі треба
знайти потік
енергії (як у
смушковому
резонаторі).
Лекція
15
Відкриті
резонатори.
Це резонатори
на основі відкритих
ліній передач.
Вони мають
електромагнітний
контакт з відкритим
простором.
Звичайно
використовуються
в лазерах сферичні
діелектричні
резонатори.
Нас цікавлять
шари діелектрика
для лінії
 .
.
тут не можна
використовувати
геометричні
наближення,
потрібно розв’язувати
рівняння Максвела.
Розв’яжемо
рівняння Максвела
для сферичного
діелектричного
резонатора.
тут потрібно
використати
ССК:

 ,
,
 .
.
В сферичній
СК не можна
перейти до
скалярних
рівнянь звичайним
чином. Використовують
заміну: ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Це – ТМ
чи Е – заміна,
оскільки
 .
.
Аналогічно
можна зробити
Н – заміну:
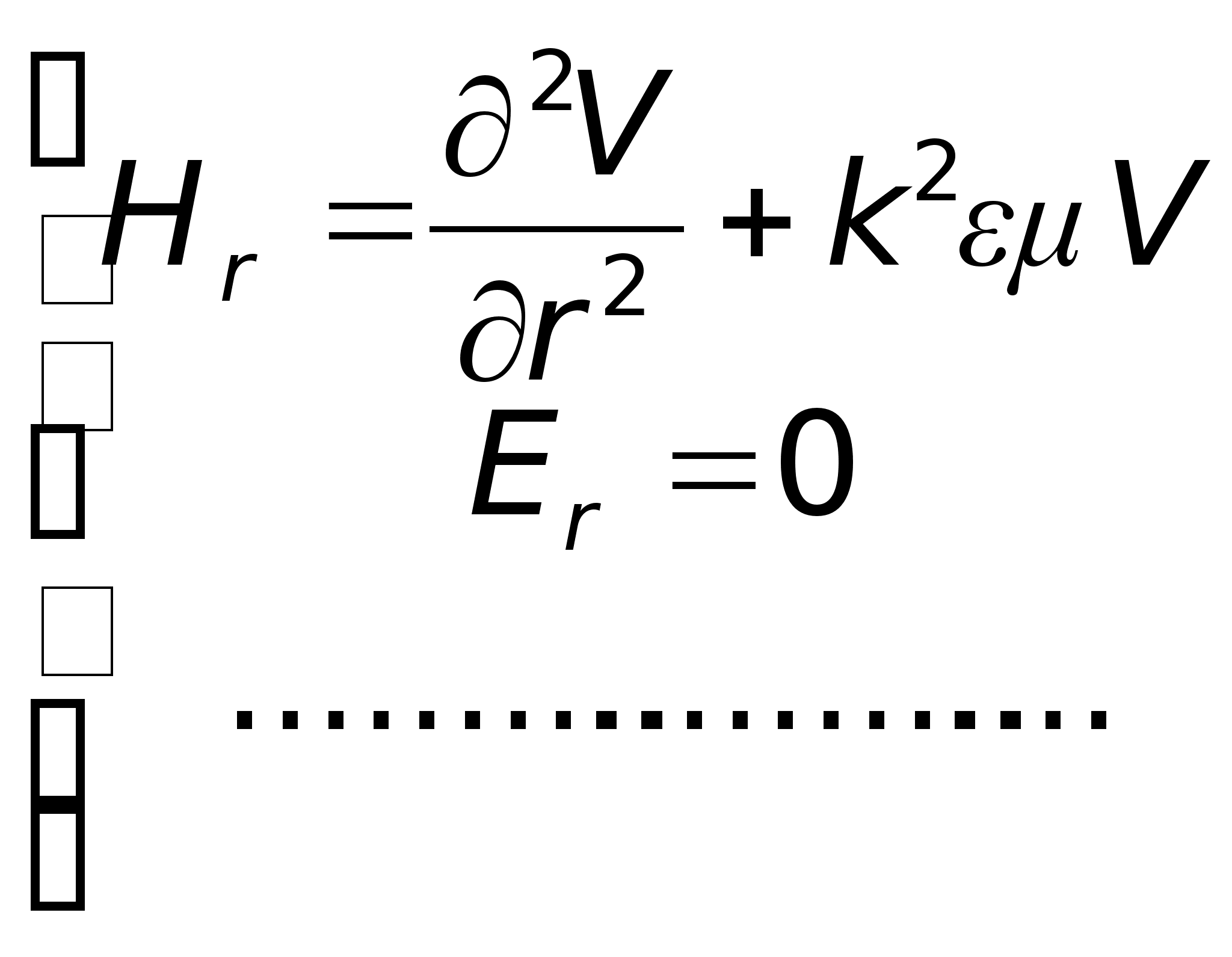
Ми будемо
використовувати
Е – заміну,
перейшовши
до потенціалу
 ,
,
в результаті
одержимо:
 .
.
Щоб отримати
саме хвильове
рівняння, де
була б ще й похідна
 ,
,
необхідно
зробити заміну:
 .
.
Потенціали

та

називають
потенціалами
Дебаю. Вони
мають методичне
значення. Розв’яжемо
простіше рівняння
для

та

— методом відокремлених
змінних:

тоді
 .
.
Рівняння
для

— це рівняння
Лежандра. Його
розв’язки –
поліноми Лежандра.
Рівняння для

можна звести
до рівняння
Бесселя заміною
 .
.
Це рівняння
для сферичних
функцій Бесселя
(або функцій
Бесселя напівцілого
вигляду). Стандартний
вигляд рівняння:
 ,
,
його розв’язки
 :
:
 .
.
таким чином
розв’язки:
 .
.
Щоб використати
граничні умови,
необхідно
виразити
 ,
,

через
 .
.
 ,
,

о тримаємо
тримаємо
два рівняння
для А та В, причому
А і В будуть
відмінні від
нуля лише тоді,
коли

системи рівна
нулю. Користуючись
виразами для

та
 ,
,
отримаємо:

з цього рівняння
отримаємо
 .
.
Для
 :
:
 .
.
Поле має вигляд:
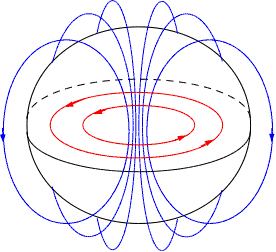
таким чином,
поля тут ідуть
таким же чином,
як і в кільці,
по якому біжить
струм.
Це була строга,
точна теорія
резонаторів
сферичної
форми. Проте,
їх важко виготовляти,
вони незручні
у використанні.
Використовують:
Розрахувати
таку систему
неможливо, бо
немає регулярних
граничних умов
(наприклад при
 ).
).
Можна вважати,
що резонансна
частота є проміжним
значенням між
резонансною
частотою у
вписаній та
описаній кулі.
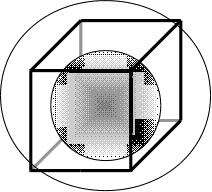
Відмінність
формування
граничних умов:
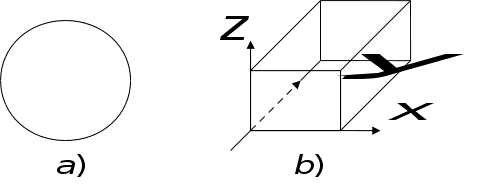

— регулярна
гранична умова
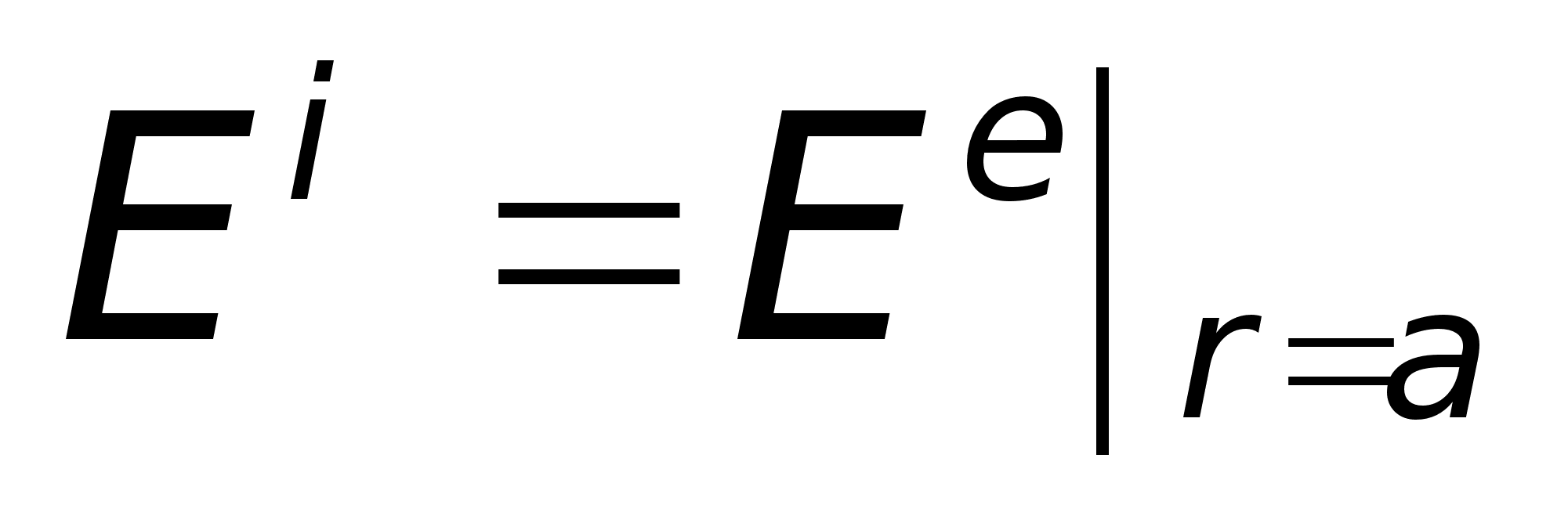

— нерегулярна
гранична умова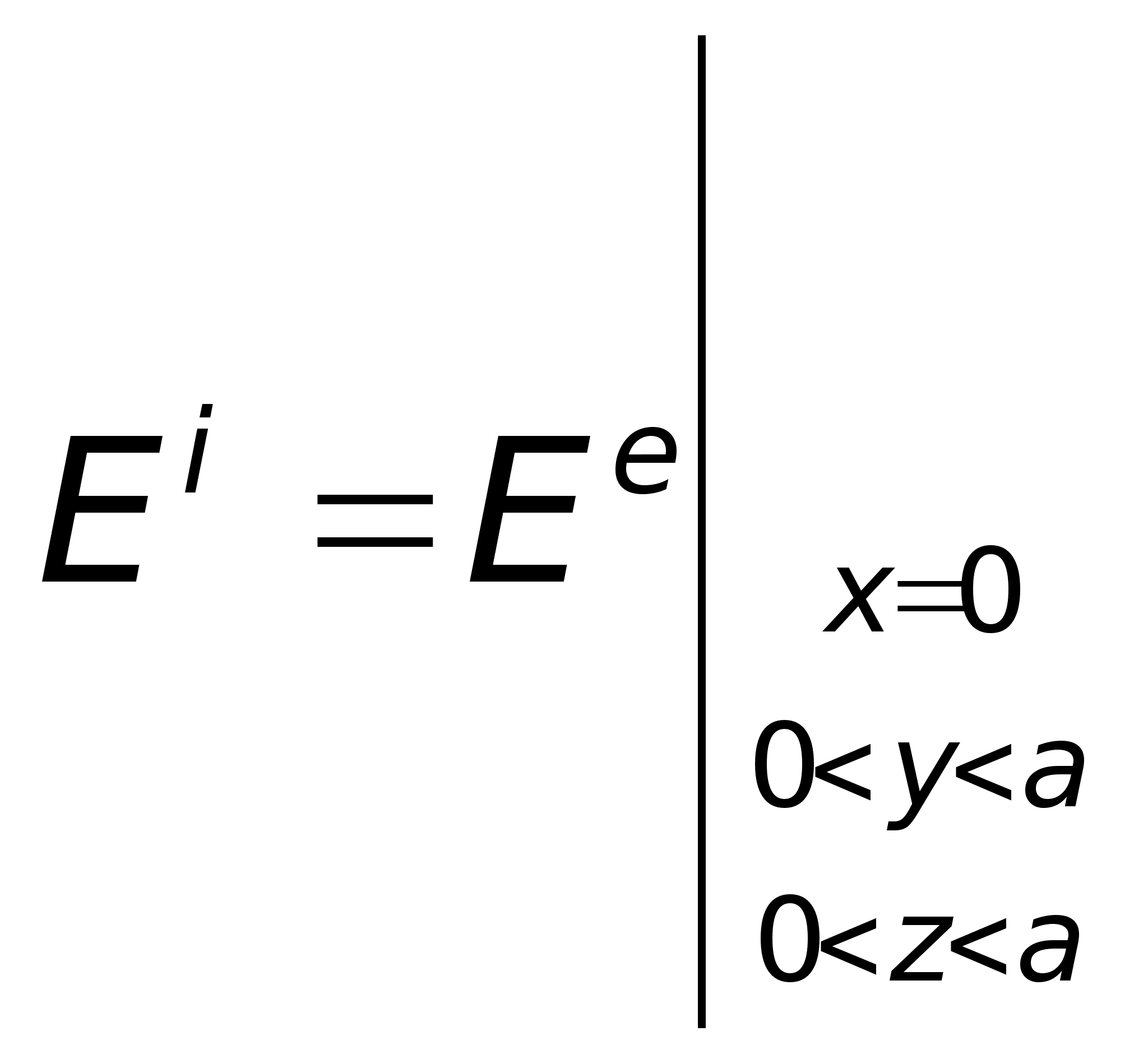
коли є
металева поверхня,
можна записати
 .
.
Це так звані
електричні
стінки.
Лекція
16
метод
магнітної
стінки.
Він застосовується
при аналізі
діелектричних
резонаторів.

Обернена
ситуація –
хвиля виходить
з металу (або
діелектрика)
в вакуум.

Зліва – стояча
хвиля, справа
– біжуча, звичайна,
зі сталою амплітудою.
Тільки
таким чином
можна досягти
виконання умов:
 ,
,
 ;
;
якщо на границі
ЕП має максимум,
а МП – мінімум
(вузол).
В середині
з великим

ЕП сильно
поглинається,
а МП залишається
сталим.
Магнітна
стінка виникає
при виході
хвилі з діелектрика
з
 .
.
Це означає, що
на межі

(на відміну від
електричної
стінки, яка
утворюється
при виході
хвилі, де
 ).
).
Метал:
 .
.
Діелектрик
 :
:
 .
.
Самостійно:
Знайти умови
існування
хвилі, частоти
за аналогією
з задачею для
металу.
Вимушені
коливання.
Лема Лоренца
і теорема взаємності.
В лінійних
полях немає
взаємодії між
полями. Однак,
існують випадки,
коли лінійні
поля впливають
одне на одне.
Уявимо, що є
два незалежних
ЕМ – процеси:
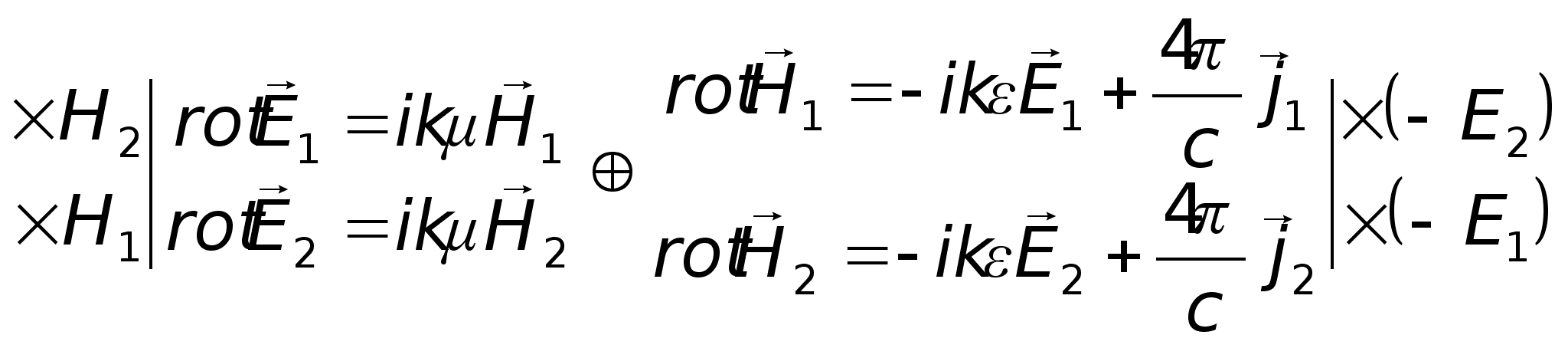
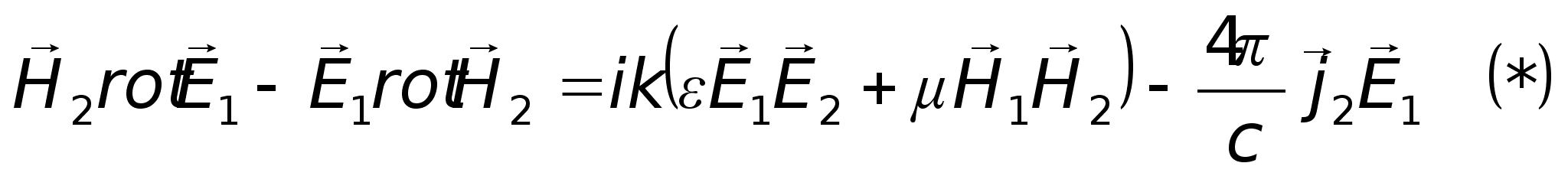
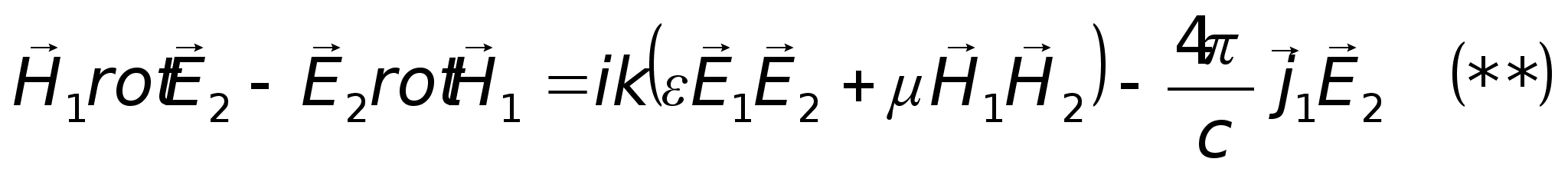
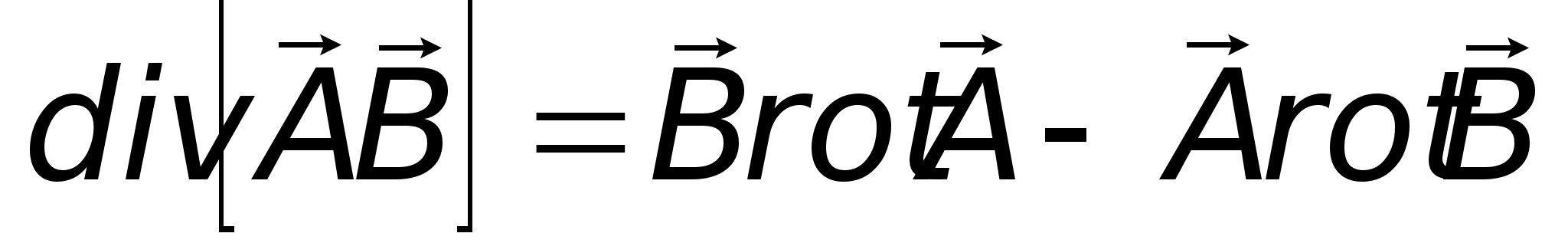

— диференціальний
вигляд леми
Лоренца.

— лема
Лоренца. (поля
не незалежні,
а залежать одне
від одного).
Р озглянемо
озглянемо
ситуацію, коли
 :
:
 ,
,
бо на

всі фотони
затухають.
 ,
,
 .
.
Р озглянемо
озглянемо
два диполі:
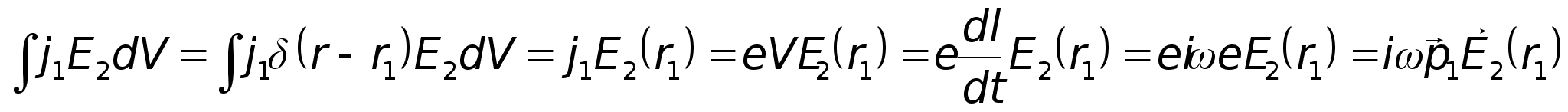

— енергія
першого диполя
у полі
 .
.

— теорема
взаємності.
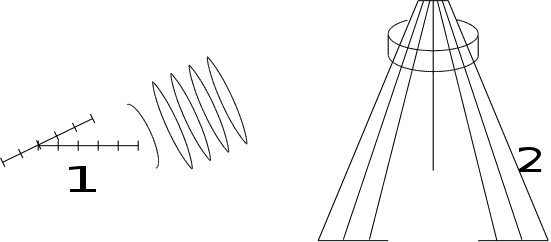
Приймач не
тільки приймає,
але й випромінює.
Для того, щоб
десь збудити
поле, потрібно,
щоб це поле
збуджувало
струм в нашій
антені тобто
потрібно розмістити
антену в центрі,
де поле найбільше.
Збудження
хвиль у хвильоводі.
У хвильоводі
можуть існувати
лише Е та Н –
хвилі.
Лекція
17
Ортогональність
власних хвиль
у хвильоводі.
Запишемо
лему Лоренца
для цього випадку.
(
— стала розповсюдження.)
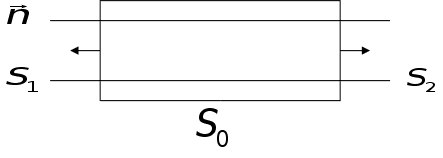
У вигляді
хвилі візьмемо
властивість
хвилі у хвильоводі:
 ;
;
 —
—
позначення.
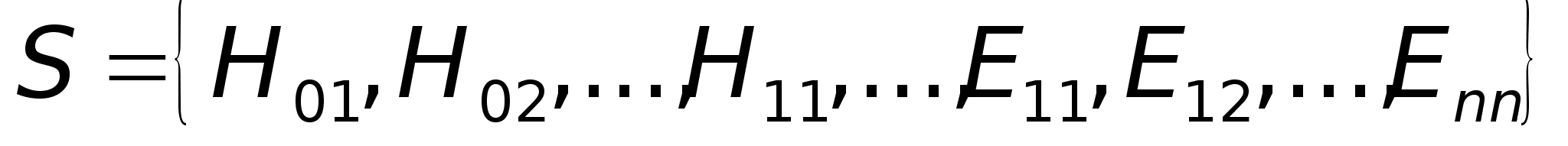
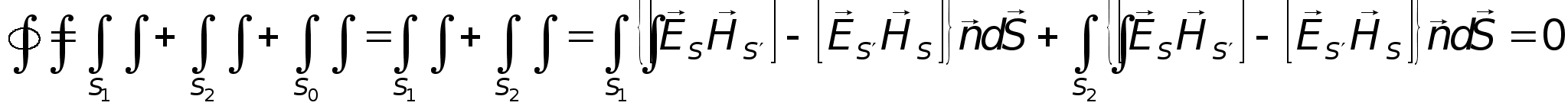
бо розглядаємо
власні хвилі
і зовнішніх
струмів немає.
таким чином:
 .
.
Незалежно
від поверхні
 .
.
Для того,
щоб це була
константа,
необхідно
 .
.
Сталість не
буде залежати
від
 ,
,
коли хвиля йде
 ,
,
і також хвиля
йде
 ;
;
для всіх інших
хвиль =0.

 .
.
Підрахуємо
норму хвилі
(співвідношення
ортогональне)
для хвилі
 .
.
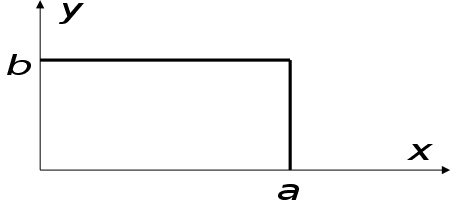
 ,
,
 .
.
 —
—
це
 .
.
Доведемо
ортонормованість.
Уявимо, що є
деякий хвильовід
і струми (див.
Мал.)
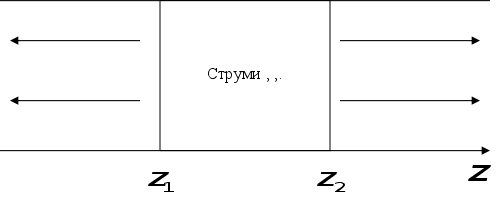
 .
.
Звернемося
до леми Лоренца.
Будемо вважати,
що:
 ,
,

— зворотна власна
хвиля.
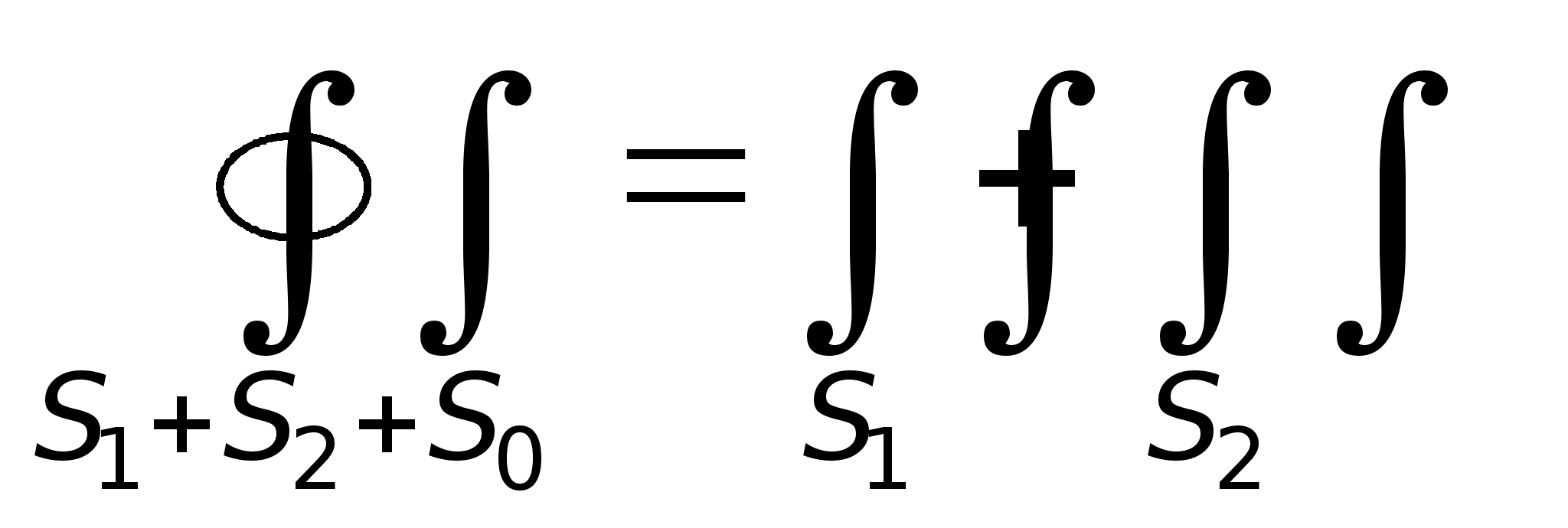
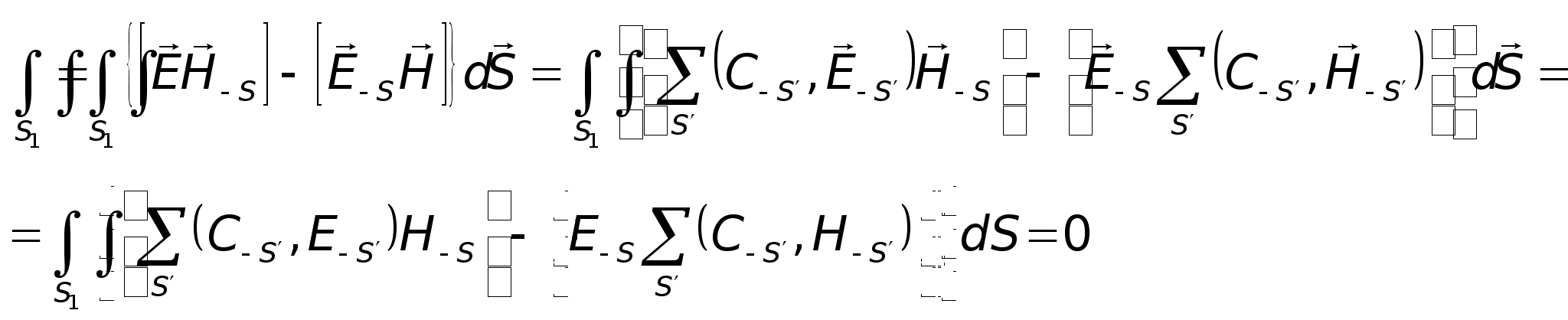
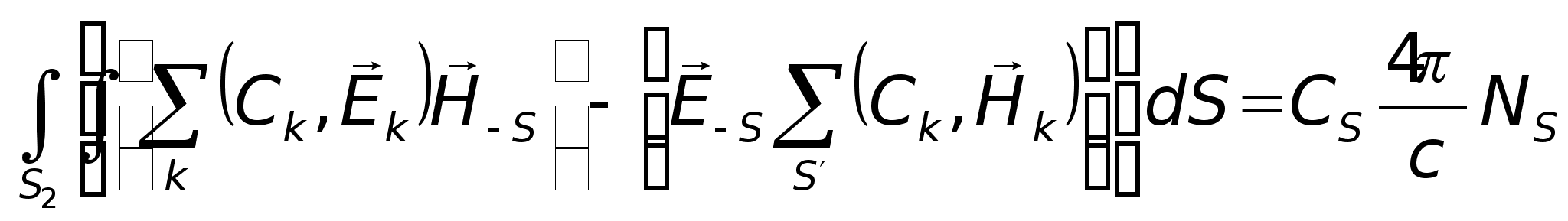
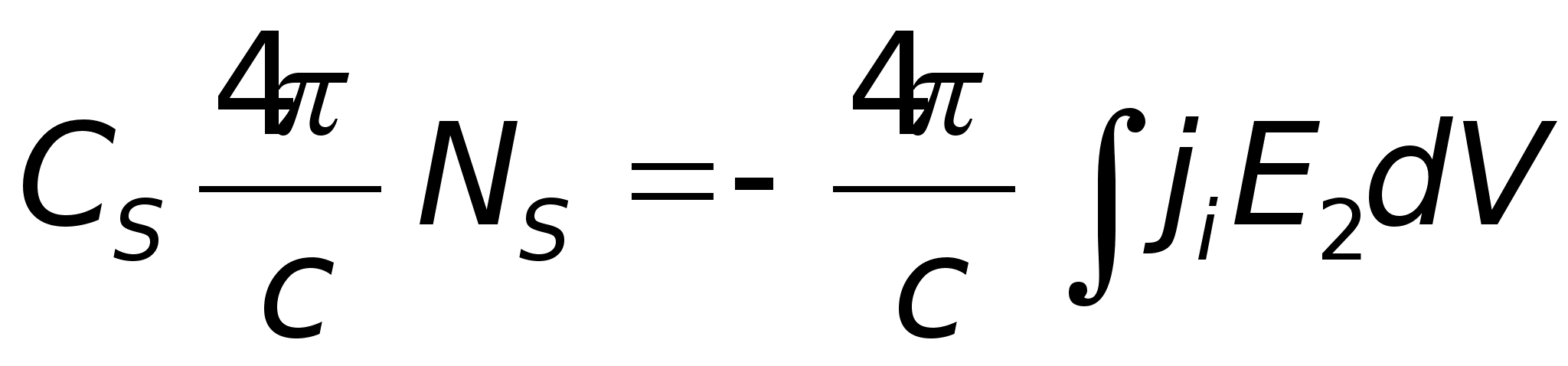

— формула
для визначення
коефіцієнтів
через струми.
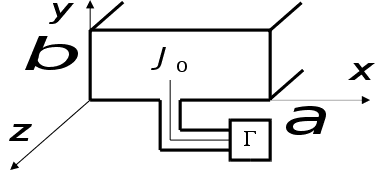
Нехай,
наприклад, у
прямокутному
хвильоводі
через отвір
у точці

введений стержень,
по якому від
генератора
Г
йде струм
 .
.
Необхідно
розрахувати
амплітуду хвилі
 .
.
 ,
,
де
 ,
,
 .
.
Отже :
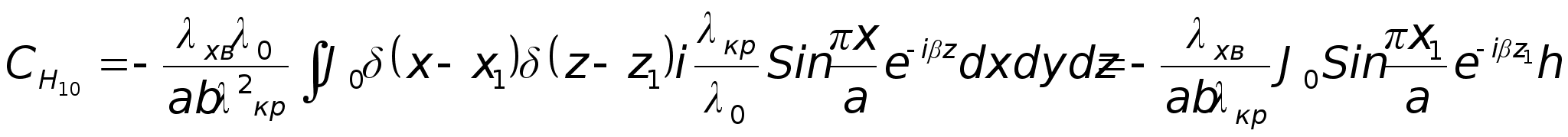
 ,
,
бачимо, що амплітуда
хвиль максимальна,
якщо
 ,
,
і дорівнює
нулю, коли стержень
коло стінки:
 .
.
Лекція
18
Збудження
об’ємних резонаторів.
ортонормованість
власних функцій
резонатора.
 ,
,
 ,
,
бо задача про
власні коливання
розв’язується
без струмів.
Для другого
коливання:
 .
.
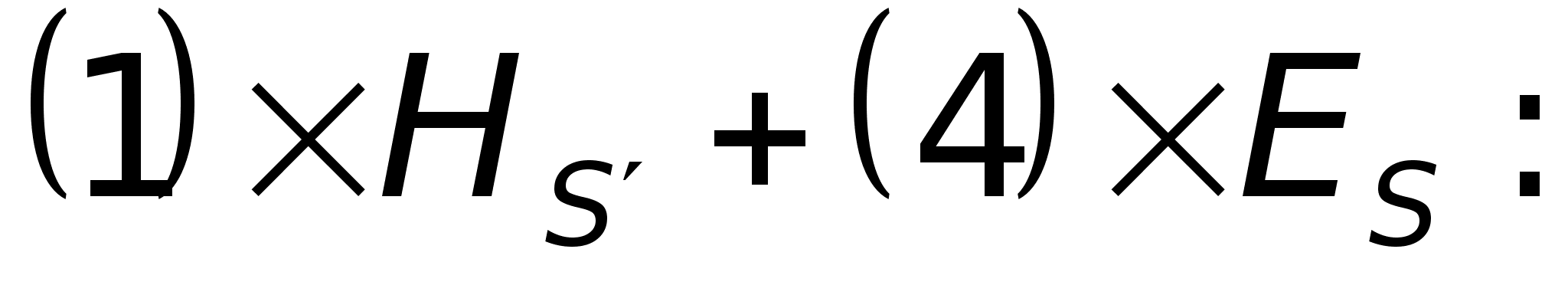
 ,
,
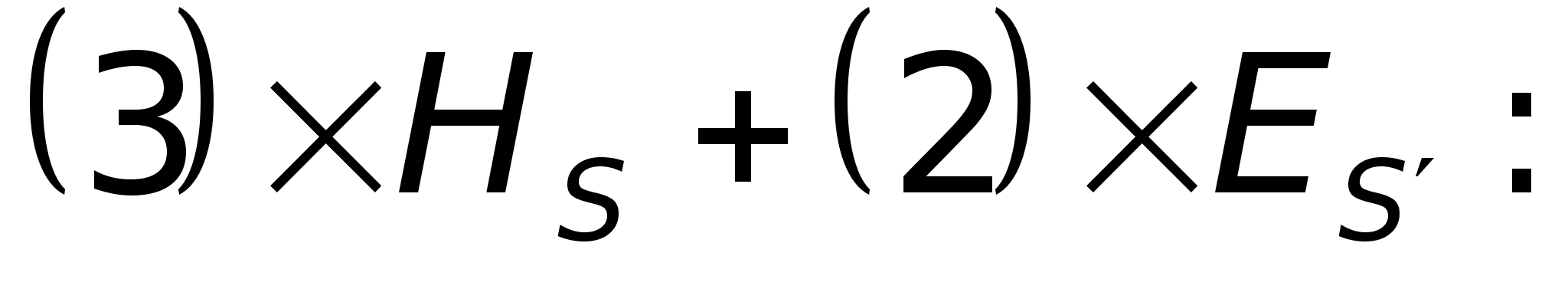
 .
.
Проінтегрувавши
обидві рівності
по всьому об’єму
та врахувавши
властивості

векторного
добутку, отримаємо:
 ,
,
 .
.
Враховуючи,
що

та позначивши

маємо лінійну
однорідну
систему відносно

з коефіцієнтами

та
 :
:
 .
.
Система має
нетрівіальні
розв’язки якщо
 ;
;
 .
.
Тоді
 ,
,
тобто
 .
.
таким чином
маємо ортонормованість
власних функцій
резонатора
з нормою
 ,
,
яку легко знайти.
Знайдемо
поля

та

всередині
резонатора
при наявності
струмів.

— рівняння
Максвела.
Псевдовектор
в математиці
– вектор, що
змінює свій
напрямок при
інверсії системи
координат
(напрямок, векторний
добуток). У фізиці
псевдовектор
змінює напрямок
при інверсії
часу
 .
.
Наприклад, при
інверсії часу
електрон починає
обертатися
в протилежному
напрямку, а
відповідно
змінює і напрямок
МП.
таким
чином, МП –
псевдовектор,
ЕП – вектор.
Звідси можна
зробити висновок,
що гамільтоніан
не може містити

(щоб він був
інваріантний
до інверсії
часу). Ще один
висновок – що
немає магнітного
п’єзоефекту.
І снує
снує
іще одна класифікація:
соленоїдальні
та потенціальні.
Потенціальний
(поздовжній):

— немає
вихорів.
С оленоїдальний
оленоїдальний
(поперечний):

— немає
вузлів.
Записавши

ми зробили
помилку, бо не
врахували
потенційні
поля, пов’язані
з електростатичними
полями зарядів,
що збуджують
струми.
Отже,
 ,
,
 ,
,
де
 ,
,
 .
.
Взагалі то,
 ,
,
бо магнітних
зарядів не
існує. Проте,
є припущення
про існування
магнітних
зарядів – монополь
Дірака;
тоді
 .
.
 ,
,
 .
.
Підставимо
в рівняння
Максвела:
 .
.
Прирівнявши
відповідні
коефіцієнти
при базисних
функціях

та
 ,
,
одержимо

— з рівняння
а). Оскільки
 ,
,
то
 .
.
 .
.
 ;
;
 .
.
таким
чином, для
гармонічних
полів:
 .
.
Тоді
 .
.
Використаємо
 ,
,
 .
.
 ,
,

бо
 .
.
таким чином,
довели строге
рівняння Пуансона
для електростатичної
частини полів.
Проінтегруємо

по
 ,
,
попередньо
помноживши
на
 :
:
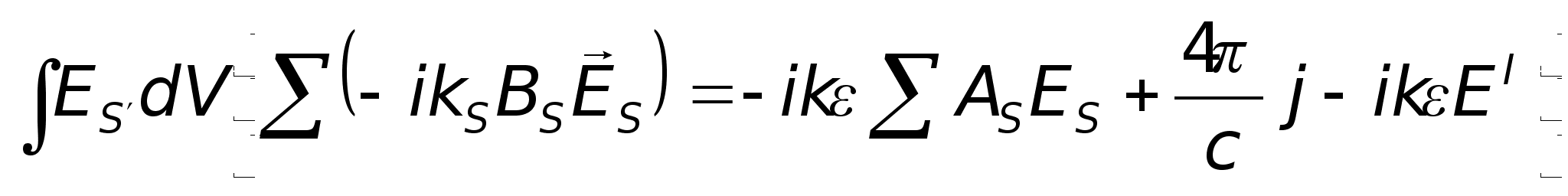
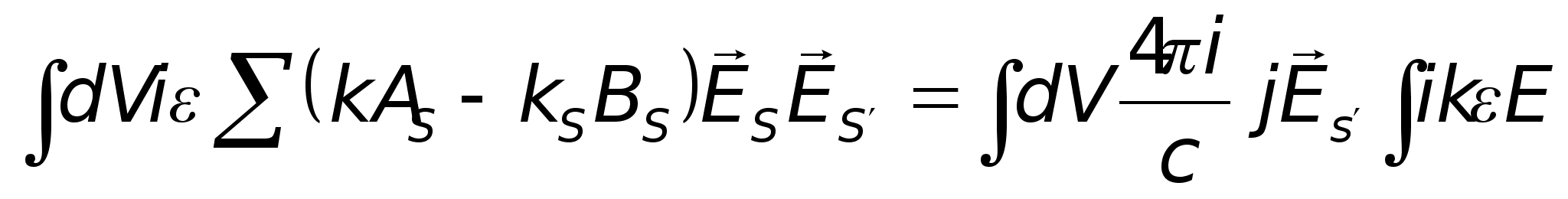
 .
.
В результаті
отримаємо:
 ,
,
маємо систему
двох рівнянь
з двома невідомими.
Амплітуда
 .
.
Ми отримали
формулу для
резонансного
збудження. тут
не враховано
дисипацію,
тому можливо
 .
.
Якщо дисипацію
врахувати
наступним
чином:
 ,
,
то отримаємо
Лоренцівську
резонансну
криву:
 .
.
Лекція
19
Неоднорідності
у хвильоводі.
Неоднорідності
є в будь-якому
хвильоводі,
вони мають
різний характер.
Для цих систем
поля можна
розбити на:
Дальню зону
(де не відчувається
неоднорідність).
Ближню зону
(неоднорідність
відчувається
суттєво).
Наприклад,
якщо буде заклепка
на стінці хвильовода,
то:
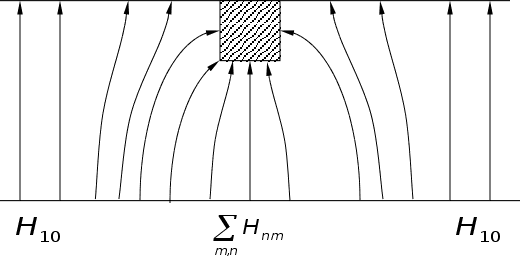
По хвильоводу
буде розповсюджуватися
лише одна хвиля

за рахунок
вибору розмірів.
Отже, біля
неоднорідності
буде зона з
енергією, яка
не розповсюджується.
Тому це деякий
еквівалент
індуктивності
або ємності.
Нам необхідно:
Розв’язати
рівняння Максвела
і знайти Г
(коефіцієнт
відбиття) і Т
(коефіцієнт
прозорості),
далі в позначеннях

та
 .
.
 ,
,
де

— лінія,
 —
—
перешкода,
тобто отримуємо

знаючи
 .
.
 .
.
Розглянемо
неоднорідність
яка називається
Діафрагма.
Вона може бути
індуктивна
чи ємнісна у
залежності
від опору.
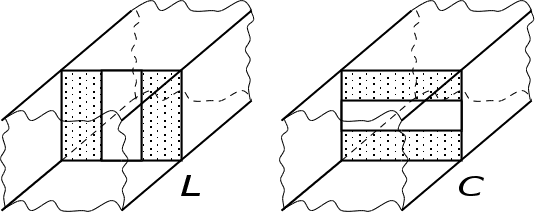
Діафрагма.
Ми розглянемо
лише індуктивну
діафрагму, для
іншої – аналогічно.
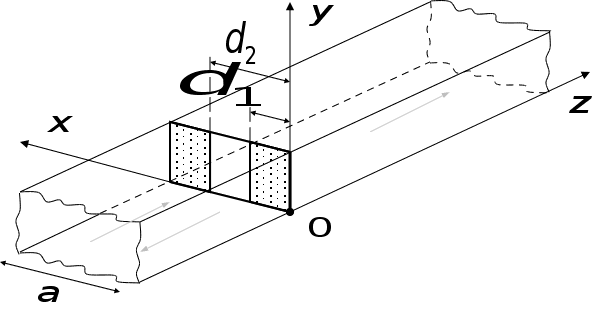
Припущення:
діафрагма
нескінченно
тонка і розташована
у площині
 .
.
Симетрія
задачі така,
що крім хвилі
Н інших хвиль
не існує.
Тоді можна
записати, що
при
 :
:
 ,
,
тобто хвиля
є сумою прямої,
відбитої (р –
коефіцієнт
відбиття) хвилі
та вищих хвиль,
що виникають
на діафрагмі.
Всі інші компоненти
розраховуються
за допомогою
системи рівнянь
Максвела:
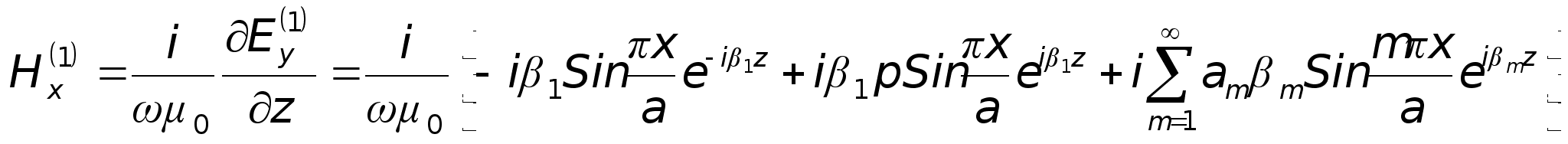
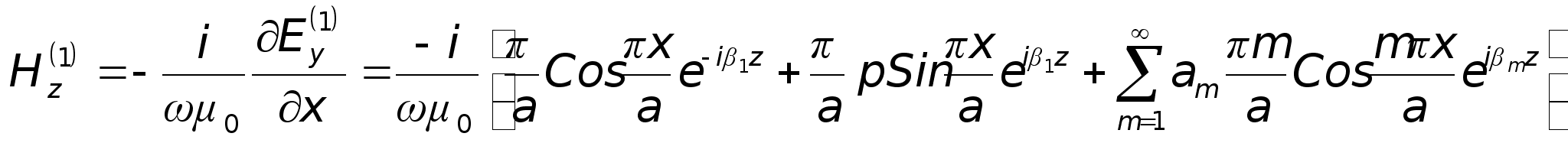
таким
чином, ми маємо
всі компоненти
поля зліва від
діафрагми.
Тепер запишемо
хвилю справа
 :
:
 ,
,
де

— коефіцієнт
пропускання
(діафрагма
генерує в обох
напрямках).
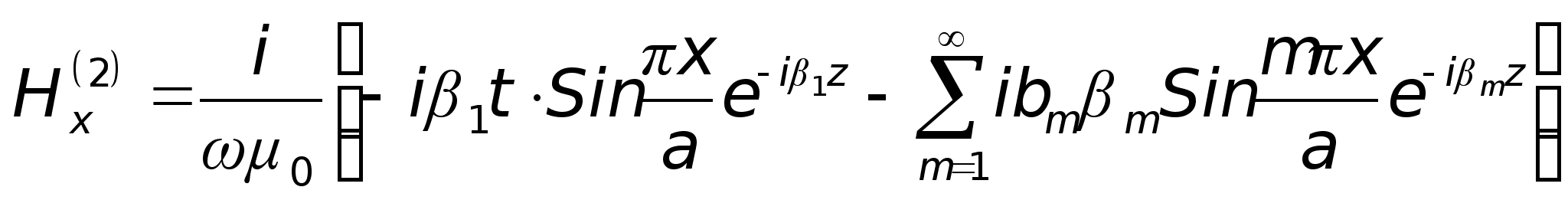
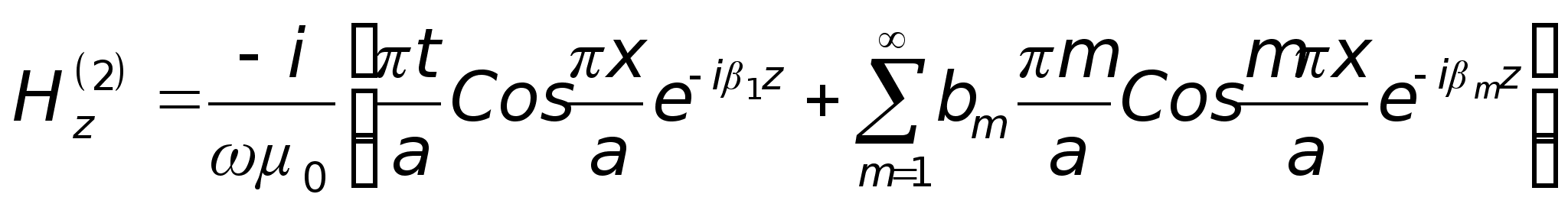
таким
чином ми розв’язали
рівняння Максвела,
не розв’язуючи
їх. (Зауваження:
ми не враховували
електростатичних
полів).
Тепер зашиємо
розв’язки
справа та зліва,
наклавши граничні
умови при

(всі поля повинні
бути неперервні):
 .
.
Розглянемо:
Граничні
умови для
 :
:

 ,
,
помножимо це
рівняння на

і проінтегруємо
від 0 до
 ,
,
в результаті
одержимо:
 ,
,
 .
.
Роблячи те
саме для поля
справа від
діафрагми
 ,
,
одержимо:
 ,
,
 .
.
Підставляючи
 ,
,
 ,
,

в рівняння для

і провівши
аналогічні
розрахунки
, отримаємо
наступне рівняння
:
 .
.
таким чином,
маємо систему
інтегральних
рівняннь (*) та
(**), можемо знайти

та
 .
.
 ;
;
 ;
;
де
 ;
;
 .
.
 .
.
Фізичні
міркування:

повинна бути

чи

в межах діафрагми.
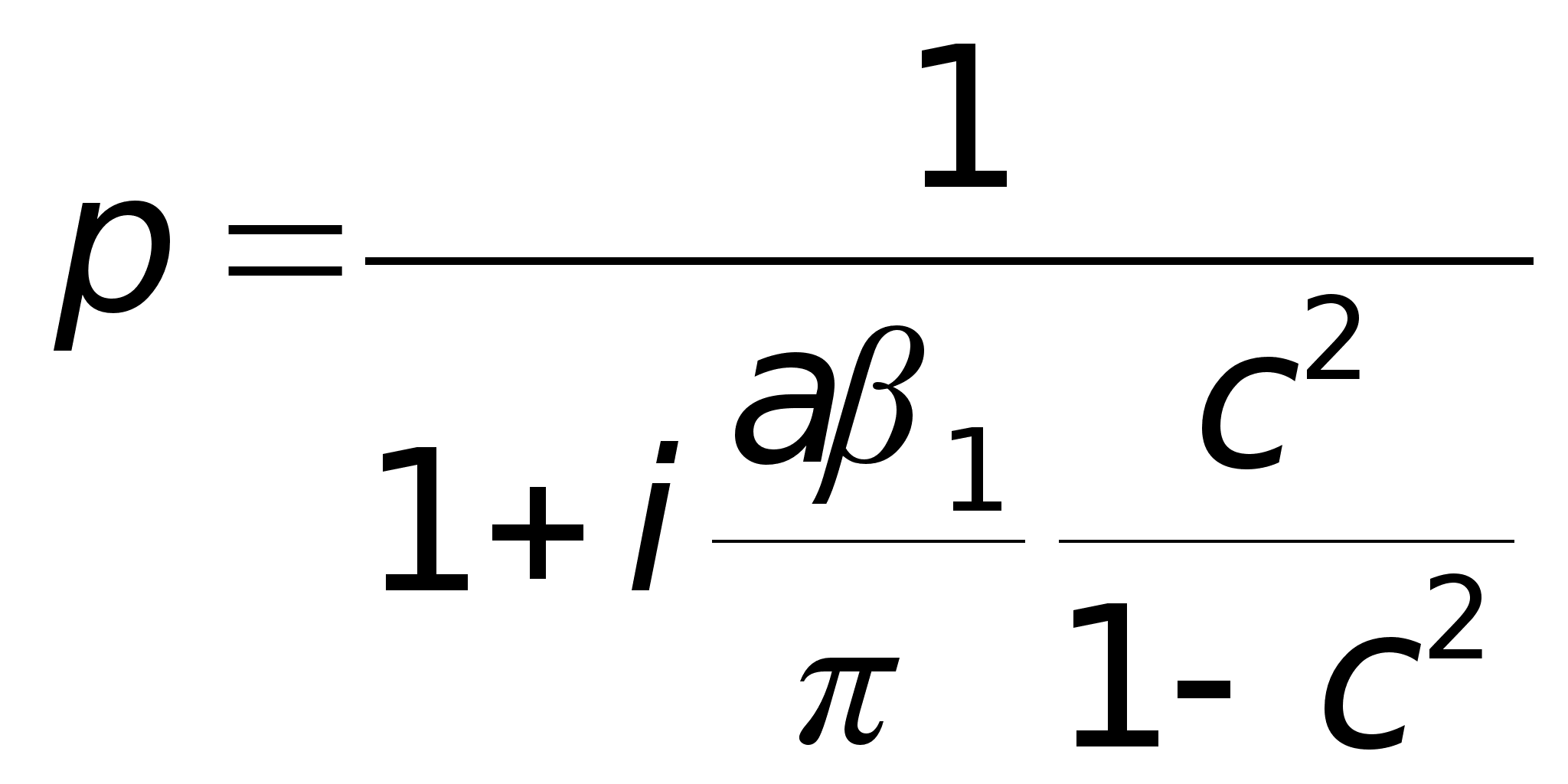
З найдемо
найдемо
 :
:
оскільки ;
;
то буде

;
 .
.
таким чином,
це дійсно індуктивна
діафрагма.
Лекція
2
Класифікація
електромагнітних
явищ
Існують
загальні підходи
для спрощення:
Рівняння
стаціонарного
електромагнітного
поля. Інколи
можна розглядати
постійні струми.
При цьому в
рівнянні (*)
зникають похідні:
 Приклад
Приклад
використання:
розрахунок
наводок.
Розглянемо
систему рівнянь
у вакуумі,
де
 .
.
Рівняння
магнітостатики:
 ,
,
рівняння
електростатики:
 .
.
Рівняння
магнітостатики
має місце і
там, де
 .Рівняння
.Рівняння
Максвела нехвильове.
Хвильовим воно
стає в однорідному
ізотропному
середовищі.
Звідси

тобто

звідки одержуємо
рівняння Лапласа:
 (з
(з
урахуванням
заряду), Пуасона:
 (без).
(без).
Квазістатичне
наближення:
 ,
,
 —
—
розмір об’єкту.
Тоді рівняння
Максвела
спрощуються.
Розглянемо
метал: там
просторові
переходи дуже
швидко зростають
(швидке затухання)
тобто частинними
похідними
можна знехтувати.
Для
монохроматичного
лінійного поля
можна використати
метод
комплексних
амплітуд:
позбавляємося
частинних
похідних тобто
спрощуємо
рівняння Максвела.
Рівняння ЕМП
в комплексній
формі будемо
розглядати
лише для лінійних
рівнянь, хоча
існує метод
і для нелінійних.
Розглянемо
рівняння: .
.
Зробимо наступну
заміну: ,
,
та аналогічно
 .
.
Підставивши
отримаємо:
 ,
,
прирівнявши
коефіцієнти
отримуємо:
 —
—
ми спростили
рівняння. Для
того, щоб записати
лінійне ДР у
комплексних
амплітудах,
потрібно: а)
замість дійсних
змінних записати
комплексні
змінні; б) замість
похідних по
часу треба
записати
 .
.
Для того щоб
знайти розв’язок
рівняння, потрібно
розв’язати
спрощене рівняння,
а потім знайти
реальну частину
від одного з
виразів:

або
 .
.
Часто рівняння
записують з
урахуванням
того, що хвильовий
вектор
 ,
,
де
 .
.
Надалі ми будемо
працювати в
комплексних
амплітудах.
Було б зручно
звести рівняння
Максвела до
хвильових, але
це можна зробити
лише у деяких
випадках, які
і розглянемо.
Плоскі
хвилі
Розглядатимемо
плоскі хвилі
в однорідному
ізотропному
середовищі.
задача:
знайти характеристики
плоскої хвилі
в такому середовищі.
Розв’язок:
Обираємо
декартову
систему координат;
Рівняння
Максвела:
 ;
;
де
 .
.
У плоскої хвилі
на хвильовому
фронті амплітуда
і фаза однакова.
Нехай хвиля
розповсюджується
в напрямку
 ,
,
то
 .
.
Отримаємо

(з
 ).
).
Розв’язок
отриманог
рівнянння
осцилятора:
 .
.
Перейдемо
до справжньої
компоненти
поля:

де
 —
—
рівняння хвильового
фронту (фаза
 ).
).
Цей фронт
розповсюджується
зліва направо.
Якби ми взяли
замість
 компоненту
компоненту
 ,
,
то одержали
б
 —
—
фронт, що рухається
справа наліво.
Розглянемо
 .
.
 .
.
 ;
;
 ,
,
тобто маємо
дійсно праву
трійку
 .
.
Оскільки
 ,
,
то
 .
.
таким
чином у плоскій
хвилі

і
 залежні
залежні
величини: якщо
одне з них задане,
то друге визначається
лише серидовищем
(див. *). Це в СГСЕ,
в інших системах
по іншому. Наприклад,
в СІ у вакуумі
 377
377
(Ом) – опір вільного
простору (хвильовий
опір простору).
Затухання
електромагнітних
хвиль (ЕМХ).
Нехай
вздовж осі
 розповсюджується
розповсюджується
ЕМХ:
 ;
;
тут

 .
.
Розглянемо
в середовищі,
де
 ,
,
(найрозповсюдженіший
випадок);
 .
.
Тоді
 .
.
З’явилася
дійсна величина
 в
в
експоненті.
Тобто кожна
хвиля затухає.
Лекція
3
Затухання
у металі, скін
– шар.
У попередньому
пункті ми записали
ЕМХ як
 ,
,
для металу
 ,
,
тоді маємо
 .
.
Оскільки
 ,
,
то
 .
.
В металі хвиля
затухає як
 .
.
Глибина, на
якій хвиля
спадає в
 раз
раз
називається
скін – шаром.
 .
.
Для постійного
поля
 .
.
Перехід
хвилі з одного
середовища
в інше.
Р озглянемо
озглянемо
такий випадок:
(див. Мал.)
Це – гранична
задача електродинаміки.
Для її розв’язку
необхідно:
Розв’язати
рівняння Максвела
у кожному
середовищі.
Прирівняти
розв’язки на
границі.
З отриманих
алгебраїчних
рівнянь одержати
всі характеристики
ЕМП.
Спочатку
обираємо повну
систему рівнянь
Максвела, однак
оскільки обидва
середовища
– однорідні
ізотропні,
можна використати
векторне рівняння
Максвела:
 .
.
Межа – пряма,
тому обираємо
декартову СК:
 .
.
У даних середовищах
буде:
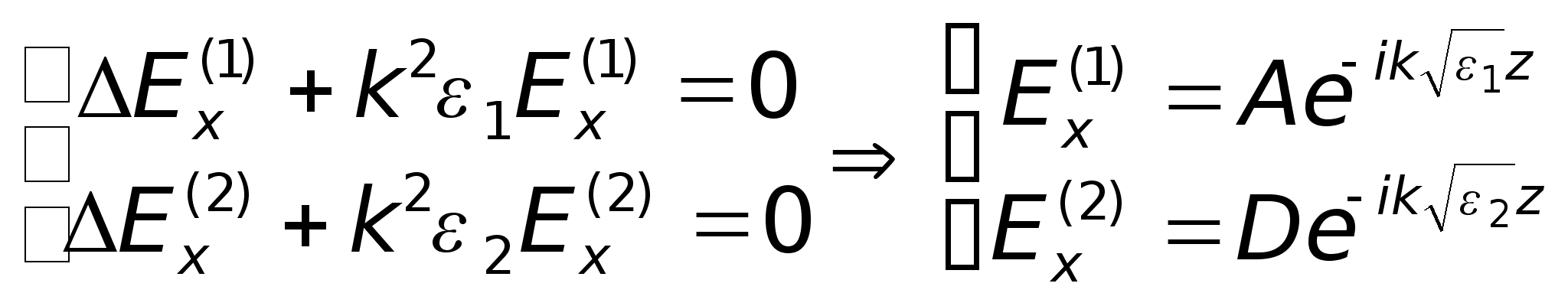
Нехай
 ,
,
тоді
 .
.
З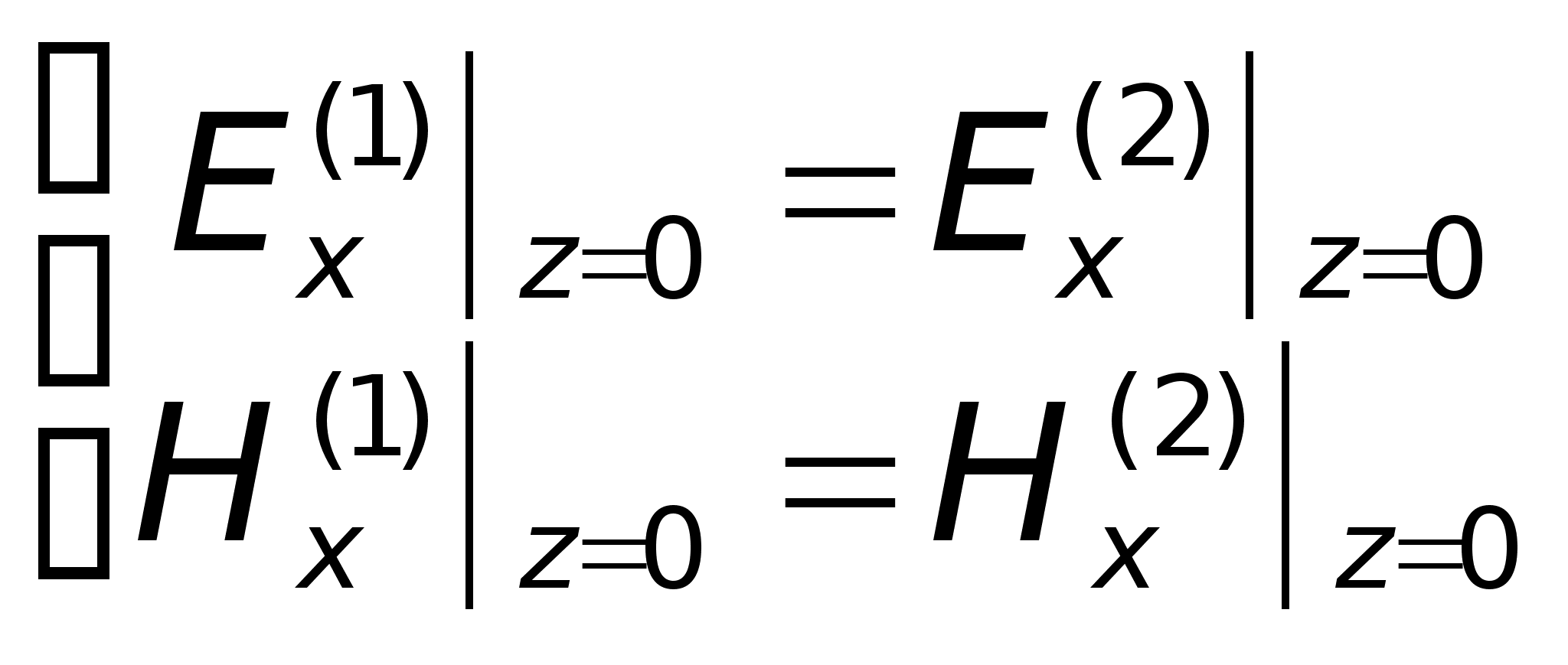
апишемо
граничні умови:
Підставивши
одержимо:
 —
—
система несумісна.
Ми не врахували
те, що існує
також відбита
хвиля у середовищі
(1):
 .
.
При відбитті
трійка векторів
залишається
правою, тому
напрямок вектора
 змінюється,
змінюється,
тому у виразі
для

— мінус:
 .
.
Підставивши
одержимо:
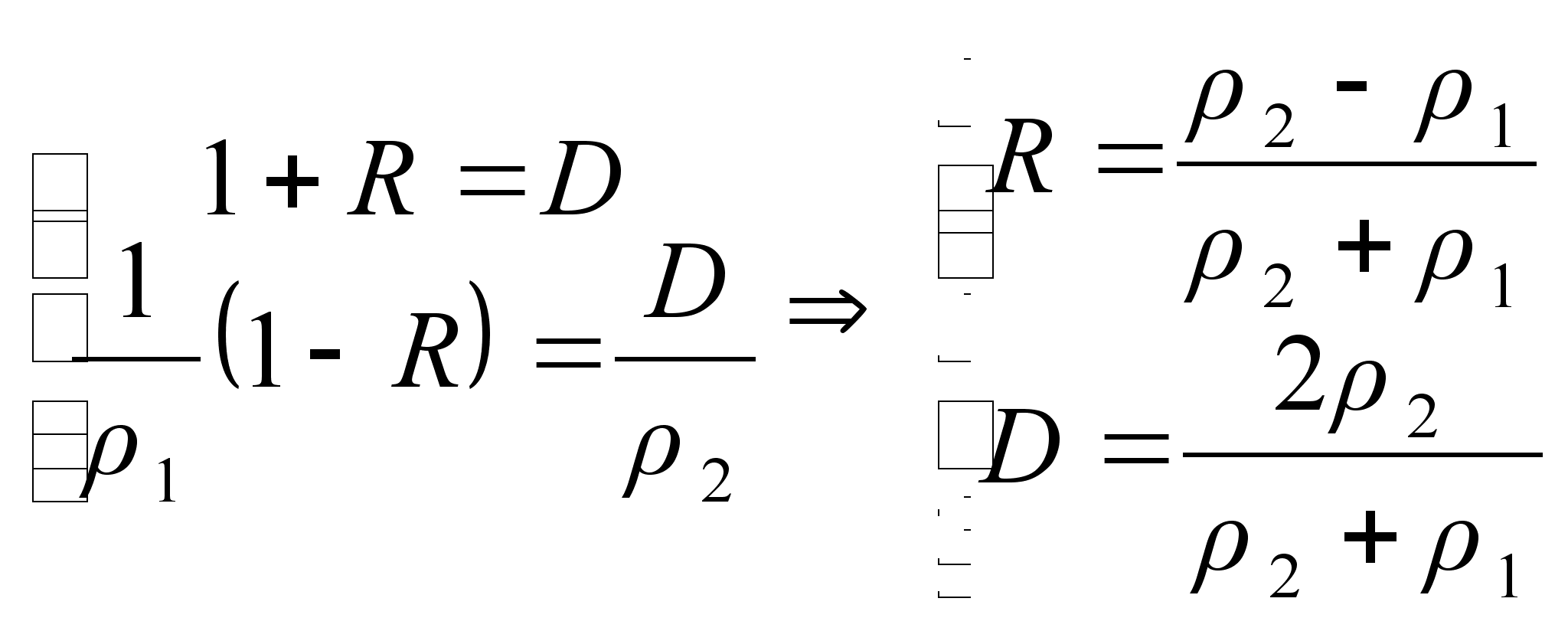
таким чином,
найбільша
(повна) передача
енергії в друге
середовище
при
 —
—
коефіцієнт
відбиття
 .
.
По аналогії
з електротехнікою
величини

називають
опорами.
Лекція
4
Узагальнена
плоска хвиля.
Для рівняння

загальний
розв’язок
 (можна
(можна
перевірити
підстановкою).
таким чином
хвиля розповсюджується
в багатьох
напрямках:
 —
—
хвиля в напрямку
 .
.
 —
—
хвиля в напрямку
 .
.
задача:
Нехай хвиля
падає під кутом
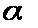
до поверхні
середовища,
знайти характеристики
відбитої хвилі
та заломленої.
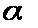
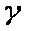
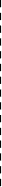

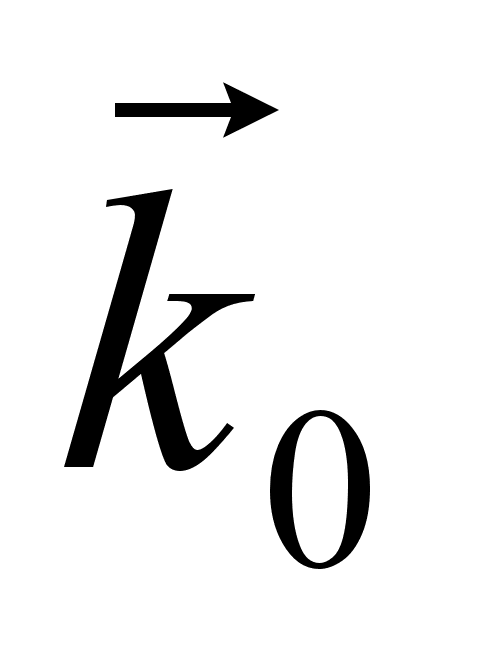



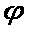

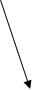
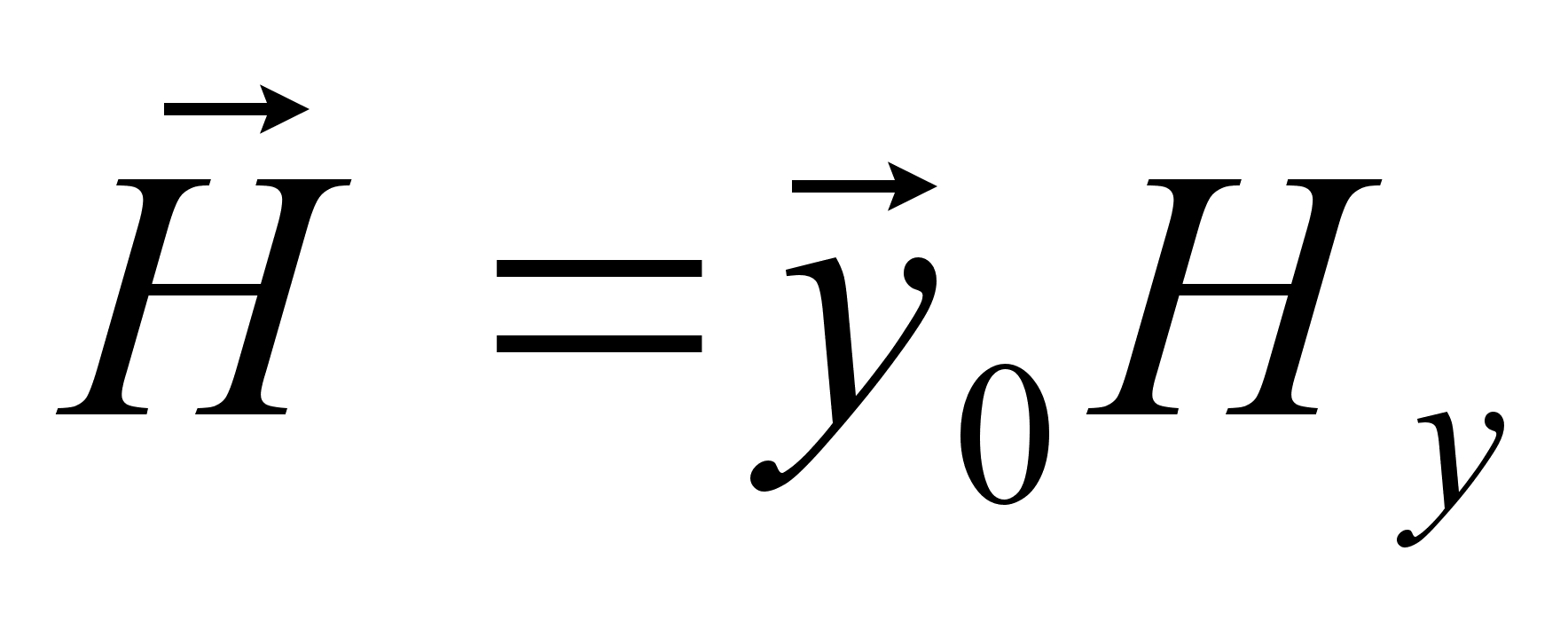
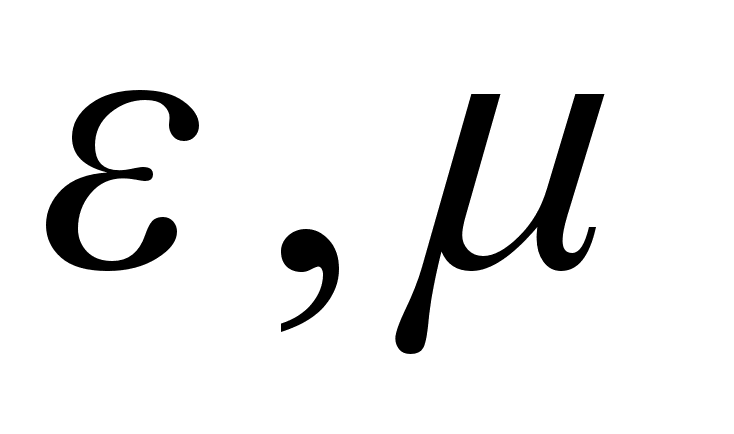


Розв’язок:
Вважаємо, що
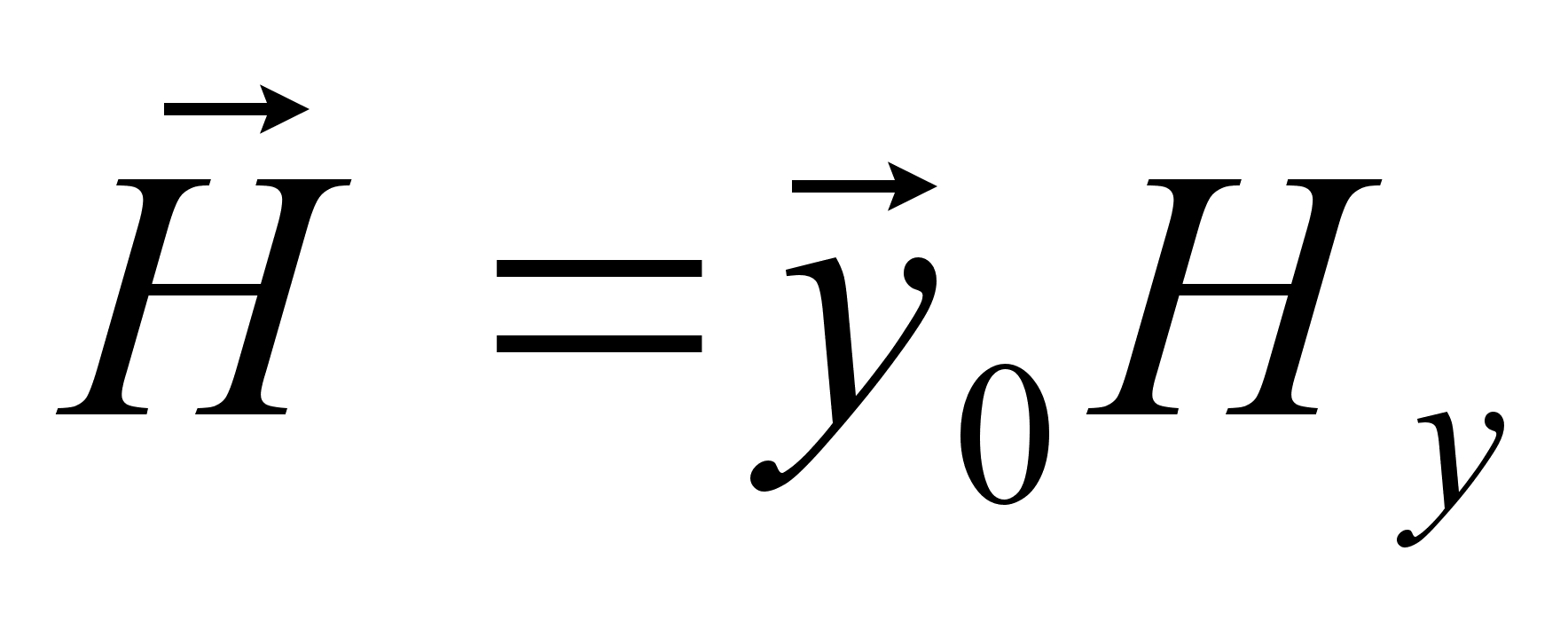 .
.
Раніше ми показали,
що розв’язком
рівнянь Максвела
є узагальнене
рівняння хвилі.
Тоді для даних
хвиль:
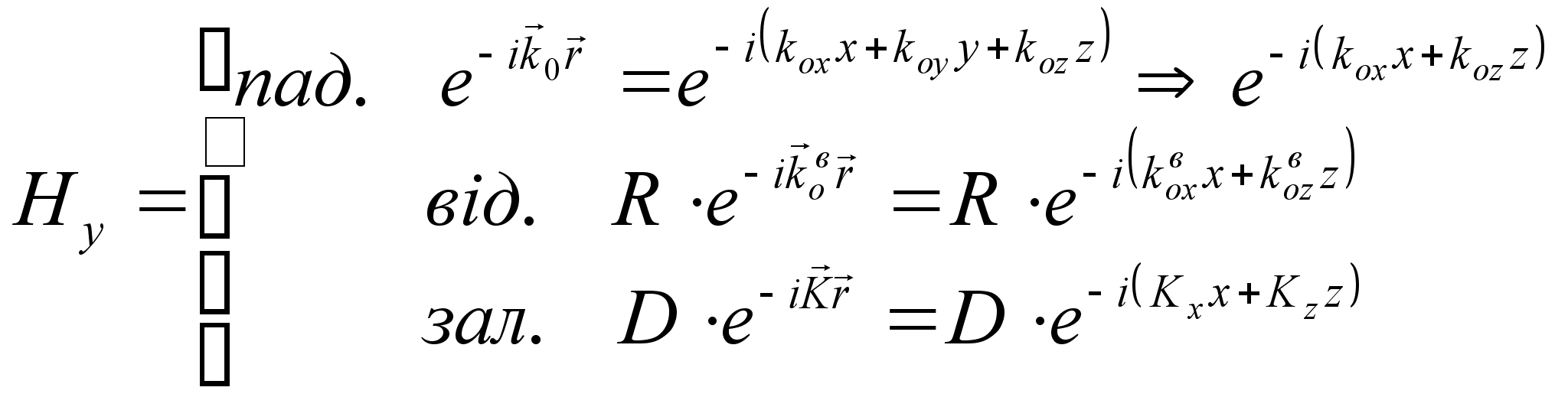
( ми розглянули
плоску задачу
в
 ).
).
Гранична
умова:
 .
.
Тоді
 ,
,
де
 ;
;
 ;
;
 ;
;
коефіцієнти

не повинні
залежати від
 .
.
В цьому випадку
 (*).
(*).
Тоді
 (**).
(**).
Виходячи
з (*), маємо
 .
.
(очевидно якщо
відкласти
відрізки на
малюнку). Аналогічно
 .
.
 —
—
перший закон

— другий закон
Смеліуса.
Наближені
граничні умови
Леонтовича.
Р
 озглянемо
озглянемо
ідеальну металеву
поверхню. Для
неї граничні
умови:
 ;
;
 .
.
Однак, тут
 —
—
не враховувалися
втрати в металі.
Їх врахував
Леонтович:
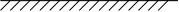
Нехай хвиля
падає під кутом
до поверхні.
Леонтович
вважав, що якби
хвиля не падала,
вона йде нормально
до поверхні.
Це можна пояснити
тим, що в металі
 ,
,
тому кут заломлення
дуже малий:
 .
.
Це наближена
умова.
Леонтович
вважав, що в
металі розповсюджується
звичайна
електромагнітна
хвиля, в якій
 ,
,
де
 .
.
Ця рівність
зберігається
і на межі металу.
У вакуумі
 ,
,
при цьому
 ;
;
 .
.
Це і є наближена
гранична умова.
В
 ідбивання
ідбиваннявід ідеально
провідної
границі (метал)
ТЕ, ТМ хвилі.

— падаюча
хвиля (індекс
“п”). Обираємо
знак “+” для
 .
.
Тоді
 .
.
Сумарне поле
над металом
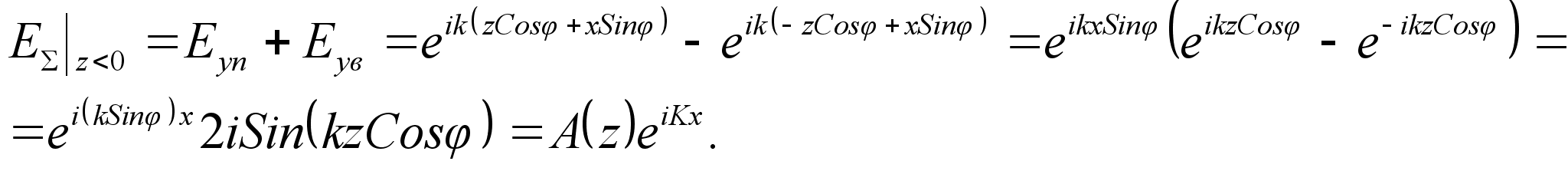
таким чином,
сумарна хвиля
розповсюджується
в напрямку
 .
.
Отже в результаті
розв’язку
рівняння Максвела
ми маємо хвилю,
що падає, і хвилю,
що відбита.
Сума цих полів
дає нову хвилю,
що розповсюджується
вздовж

і є сумою цих
двох хвиль.
Падаюча і відбита
хвиля називаються
парціальними;
Сумарна зветься
неоднорідною
плоскою хвилею.
Неоднорідна
плоска хвиля
теж є розв’язком
рівняння Максвела.
Властивості
неоднорідної
плоскої хвилі:
Ця хвиля має
поздовжні
компоненти
полів: якщо
з’являється
а)

—
 -хвиля
-хвиля
(ТЕ); б)

—
 -хвиля
-хвиля
(ТМ).
Її амплітуда
вздовж хвильового
фронту змінюється:

— через це її
називають
неоднорідною.
Плоскою називають
тому, що фронт
до напрямку
розповсюдження
 .
.
 довжина
довжина
сумарної хвилі

вихідних. Фазова
швидкість цієї
хвилі
 ,
,
оскільки в той
час, коли вихідна
хвиля а
проходить,
сумарна хвиля
проходить
 .
.
За цей же час
енергія переноситься
на відстань
 —
—
групова швидкість
 .
.

а




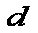


Висновок:
Існують неоднорідні
плоскі хвилі:
 ;
;
 ;
;
 ;
;
 .
.
Існують компоненти
 ,
,
 .
.
Лекція
5
Рівняння
Максвела для
Т, ТЕ, ТМ хвиль.
Для однорідного
ізотропного
середовища
в декартовій
СК:
 .
.
Т — хвиля
розповсюджується
зі швидкістю
світла,
 .
.
Для неї
 .
.
Підставимо
в рівняння
Максвела:
 ;
;
оскільки
 ,
,
таким чином
для Т – хвилі:

— рівняння Лапласа.
Для ТЕ та ТМ:
 ,
,

(хвиля розповсюджується
в напрямку
 ).
).
 .
.
Маємо

— для ТЕ, ТМ.
Ми отримали
систему рівнянь
Максвела:
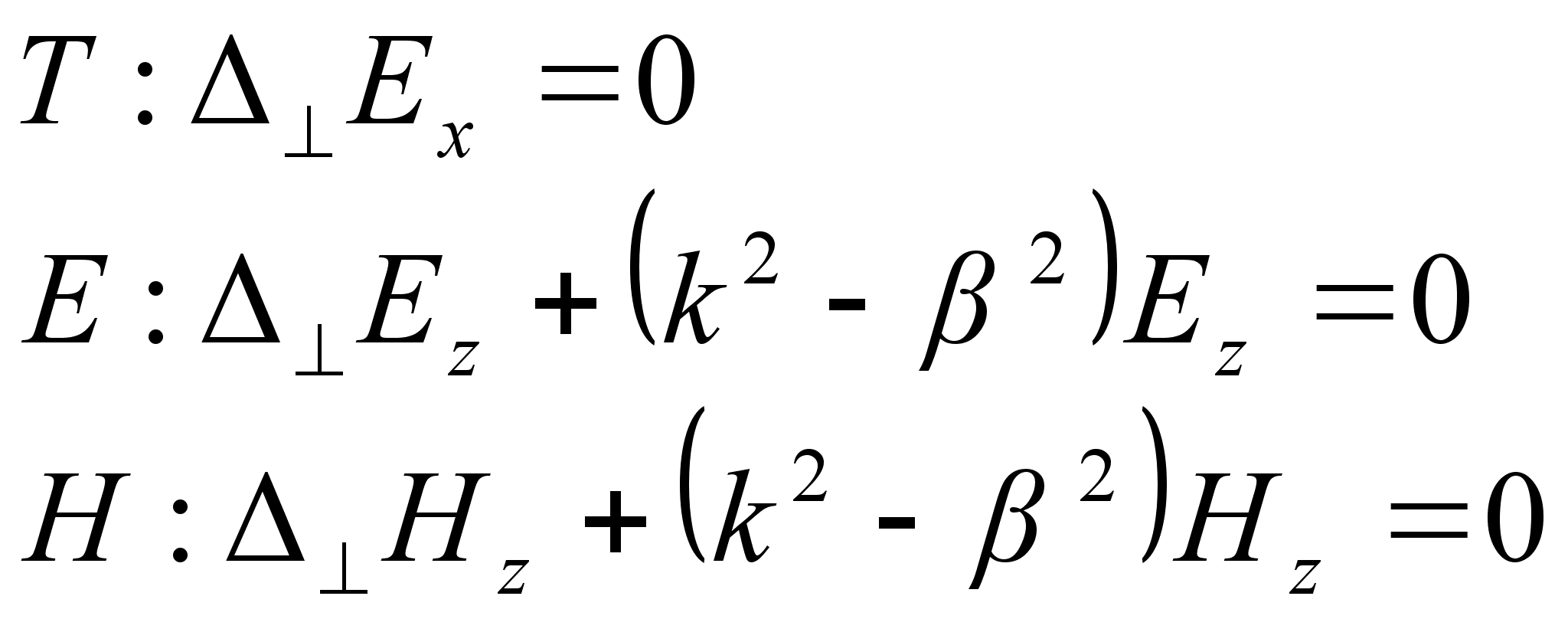
 .
.
Т – хвиля
існує там, де
є розв’язок
рівняння Лапласа
(електрика). Ми
знаємо, що рівнянням
Лапласа описується
електростатичне
поле, наприклад
у конденсаторі.
Тому якщо існує
електростатичне
поле, то може
існувати і Т
– хвиля. таким
чином вона може
існувати у
конденсаторі,
коаксіальному
кабелі.
Оскільки
одне рівняння
і однакові
граничні умови
для електростатичного
поля і Т – хвиля,
то їх силові
лінії співпадають.
Для того, щоб
розв’язати
задачу про
хвилю, треба
знайти:
Картину полів;
Сталу розповсюдження
(швидкість);
З найдемо
найдемо
ЕМ – поля між
║ пластинами:
тут може
існувати Т –
хвиля, бо існує
розв’язок
рівняння Лапласа
для конденсатора.
Картина полів
зображена на
малюнку, таким
чином ми розв’язали
задачу без
викладок. А чи
може у цій системі
розповсюджуватися
Е чи Н хвиля?
Для того щоб
відповісти
на це запитання,
необхідно
розв’язати
задачу (розрахувати
картину полів
і знайти
 ):
):
 ,
,
будемо вважати,
що
 .
.
Ми отримали
задачу Коші:
 .
.
Її розв’язок
 .
.
 ;
;
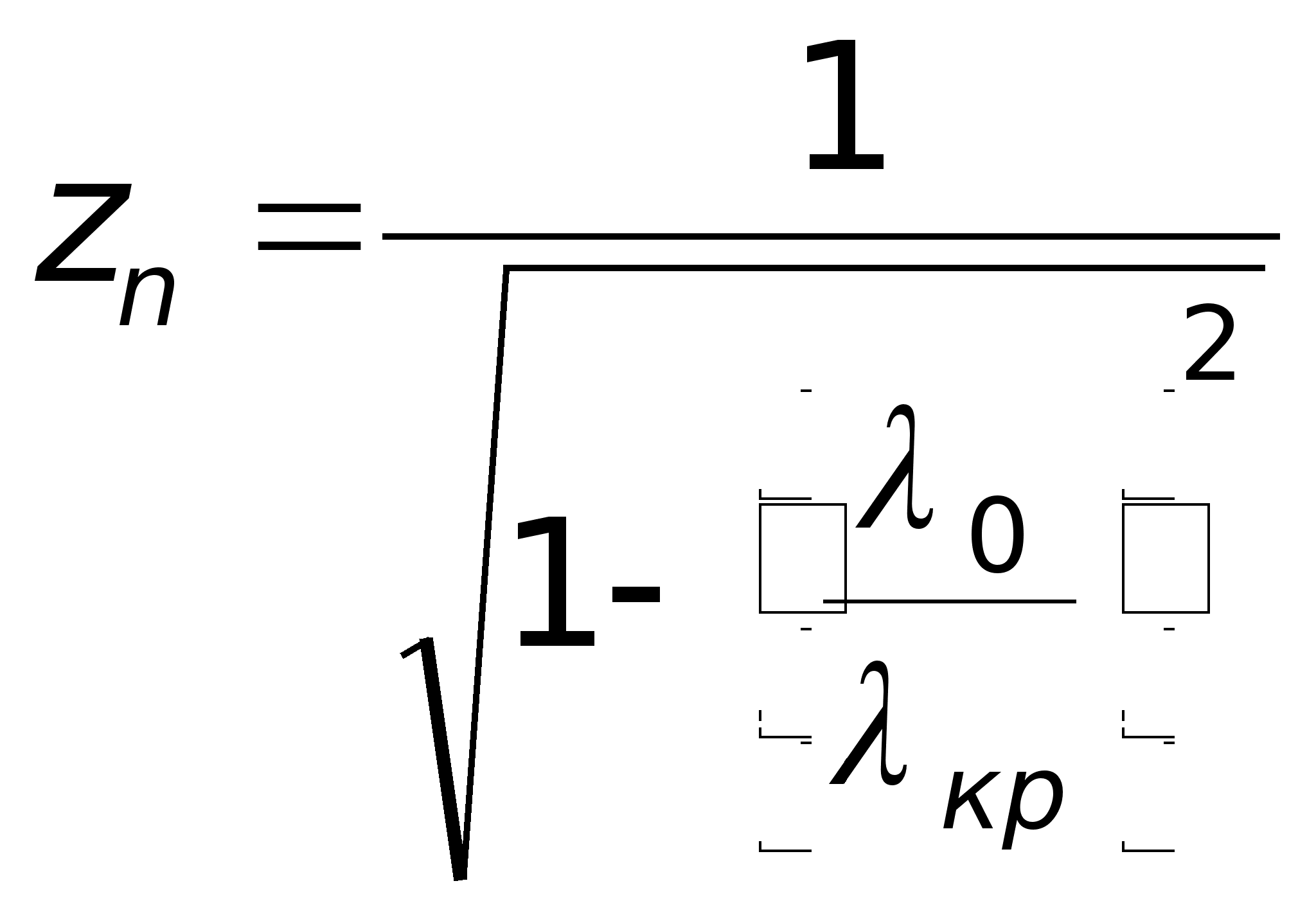
 .
.
 .
.
 .
.
Де
 —
—
довжина хвилі
у хвилі у хвилеводі.
очевидно,
що
 при
при
 ;
;
тобто існує
деяка критична
довжина хвилі
 —
—
така, що при
 хвиля
хвиля
не буде розповсюджуватися
у хвилеводі:
при
 :
:
 —
—
уявне, тобто
присутнє затухання.
 ;
;
нижня
 .
.
таким чином
у хвилевід
зайде Т – хвиля
з будь-яким

і Е – хвиля лише
з
 .
.
Можна отримати,
що
 .
.
Якщо зменшувати
 ,
,
то

збільшується.
Також змінюється

при зміні
 .
.
Існує критична
частота, коли
 ,
,
тоді хвиля не
розповсюджується.
 —
—
довжина Т –
хвилі у вільному
просторі
 ,
,
 ;
;
таким чином,
в результаті
розв’язку
рівняння Максвела
ми знайшли лише
одну компоненту
хвилі
 .
.
Однак для побудови
картини необхідно
знайти всі інші
компоненти
(у ТЕ та ТМ хвиль
може бути не
більше п’яти
компонент).
Скористаємося
рівняннями
Максвела: будемо
виходити з
 .
.
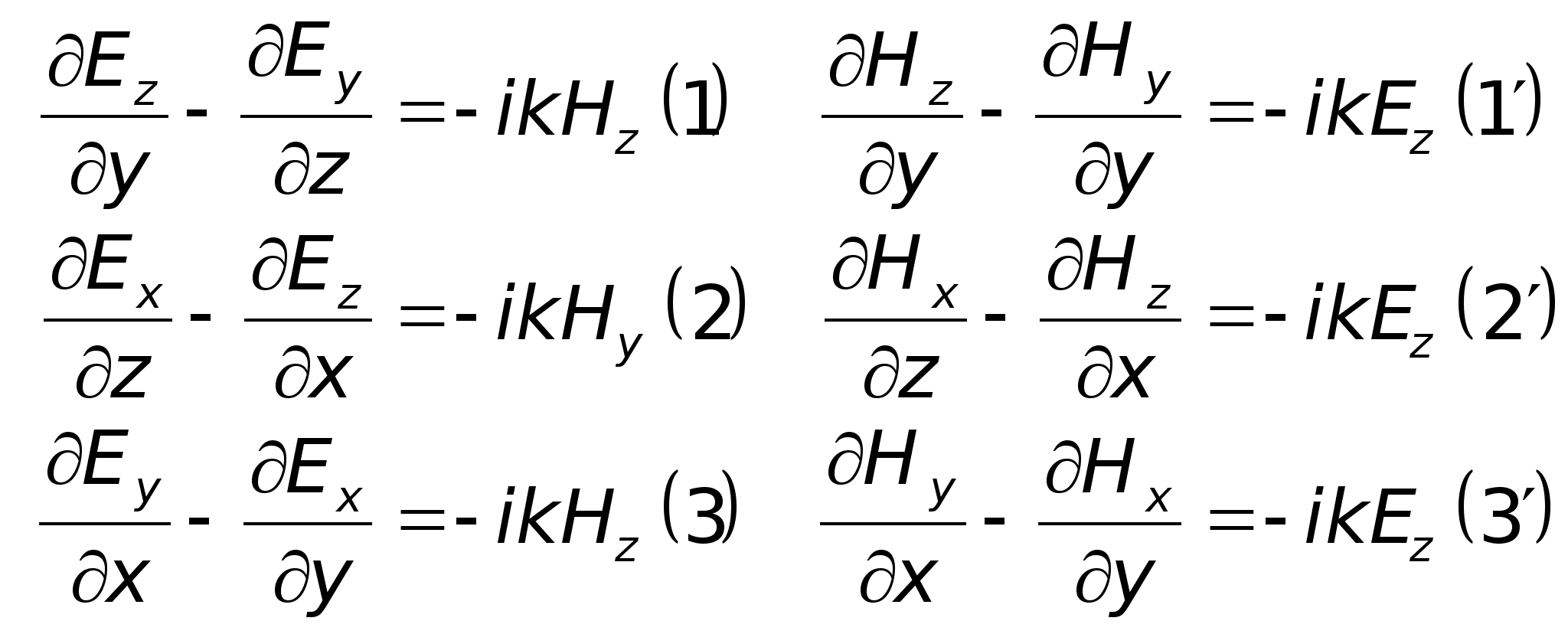
А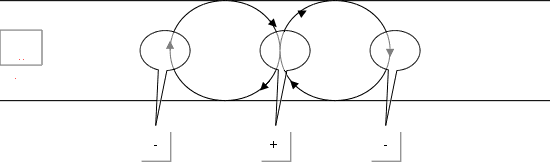
 налогічно
налогічно
для
 ,
,
таким чином,
для неоднорідної
хвилі ми отримали
повний розв’язок:
 .
.
Розглянемо
пари:
 .
.
В нашій Е – хвилі
обов’язково
 ,
,
тоді з системи
легко отримати
інші компоненти: .
.
Таким чином
маємо картину
полів ТМ (Е –
хвилі). Для ТЕ
– хвилі – аналогічно.
Лекція
6
П
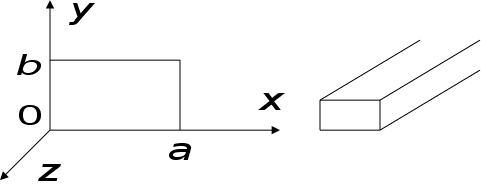 рямокутний
рямокутнийхвильовід.
В середині
металевого
проводу не може
бути електростатичних
полів. Можуть
бути лише Е, Н.
 .
.
Граничні умови:
 Нехай
Нехай
 ;
;
тоді
 ;
;
 ;
;
 ;
;
 ;
;
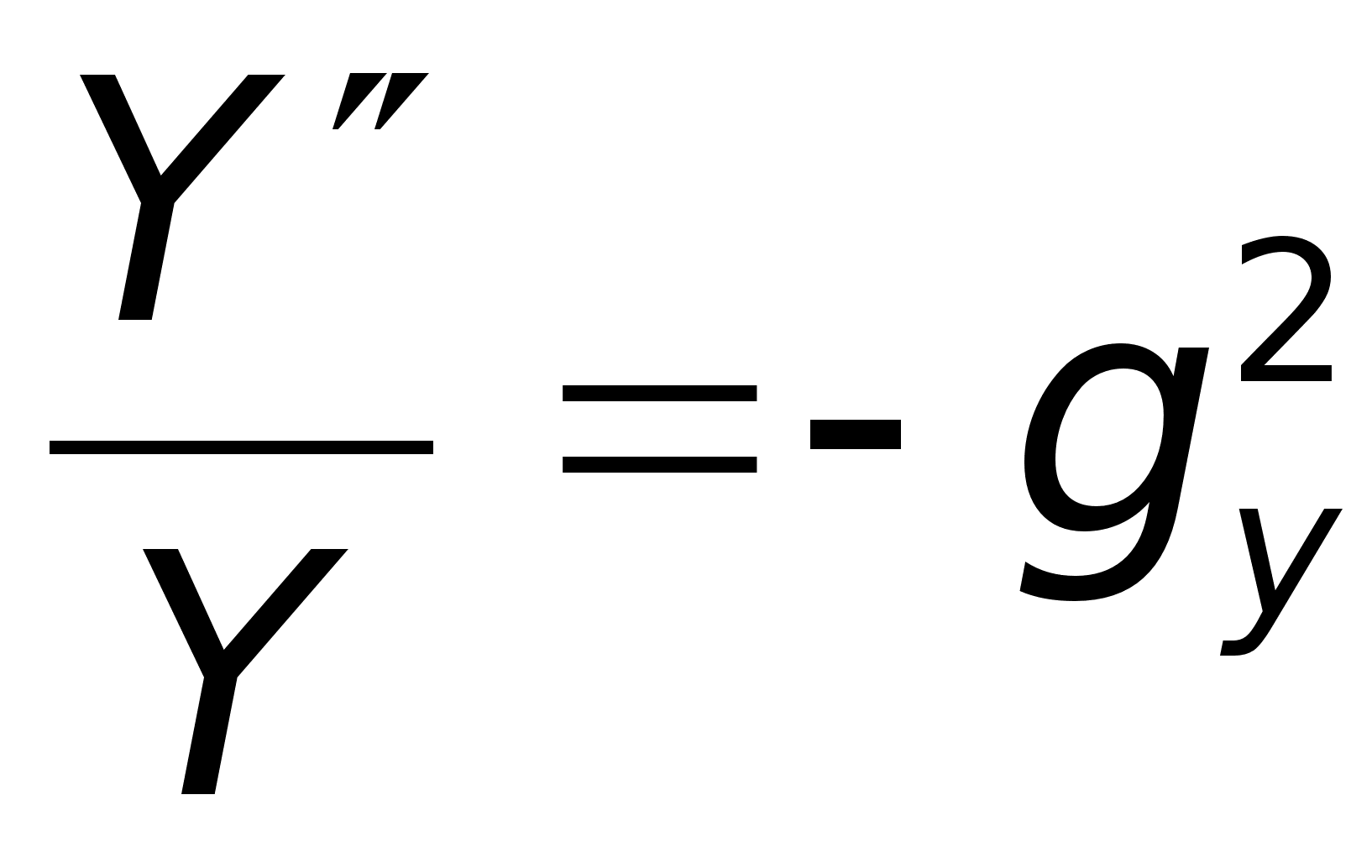
 .
.

таким
чином
 .
.
 .
.
Тут
 ;
;
звідси
 .
.
Аналогічно
 .
.
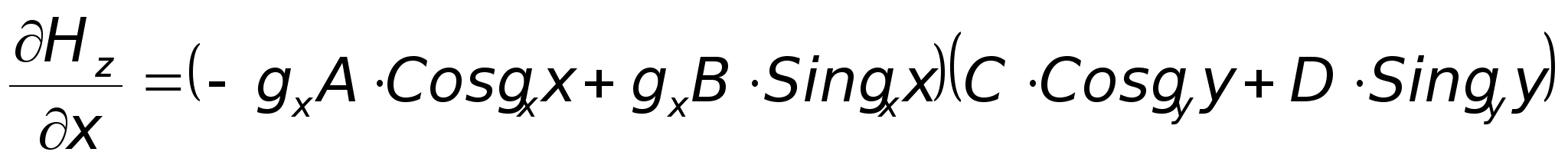

за симетрією
 .
.
 отже
отже
 .
.
 .
.
Розв’язок:
 ;
;
де
 ,
,
можна також
знайти
 ,
,
але
 .
.
Ця задача
в частинних
похідних має
безліч розв’язків
 .
.
Загальна хвиля
буде
 .
.
Розглянемо
один з розв’язків:
 -це
-це
хвиля
 .
.
Отримаємо
 .
.
Інші компоненти:
 ,
,
тут
 .
.
У хвилеводі
будуть розповсюджуватися
хвилі з
 .
.
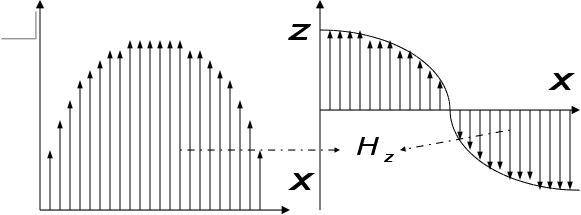
Визначимо
фізичний зміст
індексів: розглянемо
 .
.

— по

одна півхвиля.
Таким чином,
перший індекс

означає скільки
варіацій має
поле в напрямку
 .
.
Другий індекс
 —
—
вздовж
 .
.
Розглянемо
типову картину
полів у хвильоводі
для
 :
:
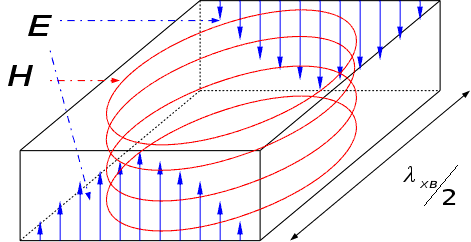
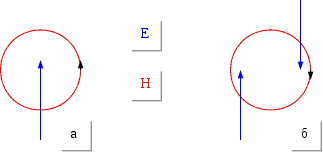
Оскільки
хвиля рухається
з певною швидкістю,
 зсунуте
зсунуте
в часі на

(в формулі це
 ),
),
тому маємо
картину не а)
а б).
Для хвилі
 :
:
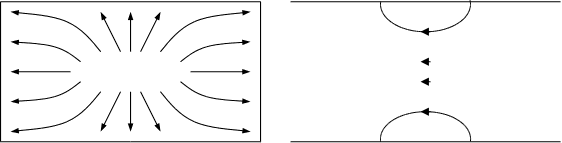
Для хвилі

завдяки граничним
умовам на стінках
 ,
,
а по певній
координаті
(там, де індекс
= 0 ) це поле однорідне,
тоді
 буде
буде
всюди, тобто
цієї хвилі не
буде.
Лекція
7
Хвильовий
опір хвильовода.
Для Т –
хвилі:

(для вакууму).
Для ТЕ, ТМ хвиль
введення хвильового
опору не є
однозначною
задачею, бо
існує кілька
компонент.
Домовились
відносити опір
до поперечної
компоненти:
 .
.
Електродинамічні
потенціали
Векторний
і скалярний
потенціали
вводяться
наступним
чином:
 ;
;
 .
.
У першому рівнянні,
очевидно,

можна задавати
з точністю до
 .
.
При цьому рівняння
Максвела:
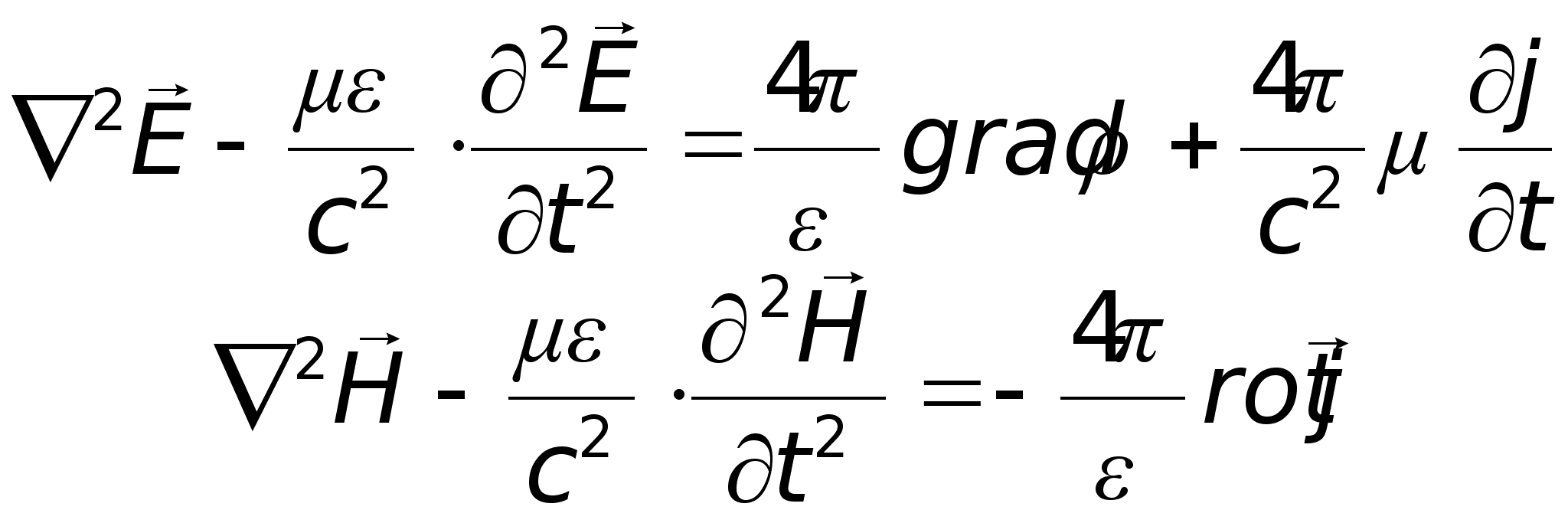
Тоді отримаємо
рівняння для
ЕД потенціалів:
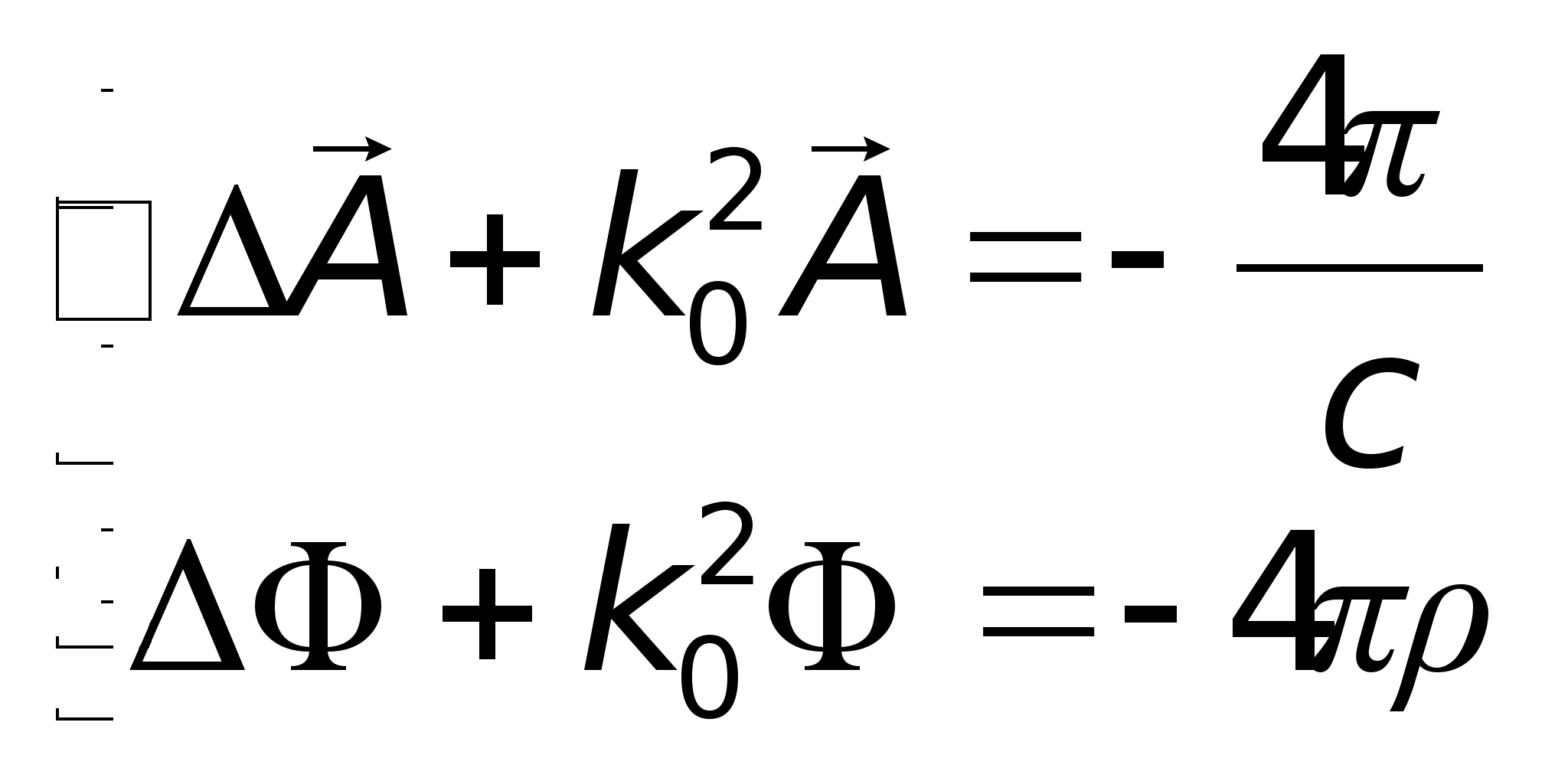
Рівняння
для Т, ТЕ, ТМ хвиль
різні. Щоб звести
їх до одного
виду, використовуючи
потенціали
 ,
,
 ,
,
де
 —
—
електрична
скалярна функція,
 —
—
магнітна скалярна
функція. Якщо
для Т – хвилі

завжди, то
 ,
,
а

перетворюється
в нуль завдяки
 .
.
Рівняння для
 :
:
 .
.
При цьому
компоненти
 .
.
Інші
компоненти
можна отримати
методом, який
розглядався
раніше. Для
циліндричної
СК:
 .
.
Круглий
хвильовід.
очевидно,
будемо користуватися
циліндричною
СК
 :
:
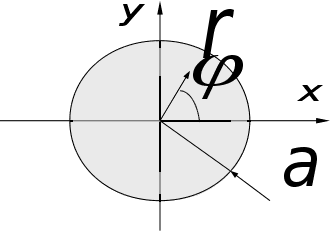
Шукатимемо
хвилю
 .
.
Можна розв’язати
 ,
,
однак ми розв’яжемо
рівняння для
скалярних
потенціалів:
 .
.
З урахуванням
вигляду оператора
Лапласа у
циліндричній
системі координат
одержимо:
 .
.
Використаємо
метод відокремлення
змінних:
 ;
;
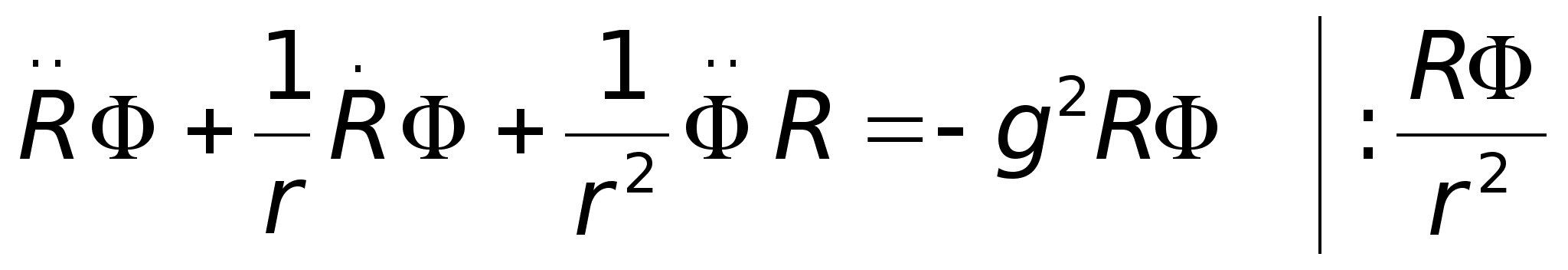
 .
.
Звідки очевидно,
що:
а)
 ,
,
тут

— будь-який кут
повороту, залежить
лише від вибору
координат
(з’явився через
симетрію задачі).
Оберемо
 .
.
б)
 —
—
ЛДР зі змінними
коефіцієнтами,
тому звичайним
шляхом його
розв’язувати
неможливо;
потрібно застосувати
спеціальні
функції. Приведемо
рівняння до
стандартного
вигляду: заміною

воно зводиться
до рівняння
Бесселя:
 .
.
Його розв’язками
є циліндричні
функції (функції
Бесселя):

(*)
Функції
Неймана
 ,
,
а тому очевидно,
що
 ,
,
тому що поле
при

повинно бути
скінченим.
таким чином,
якщо в задачі
існує точка
 ,
,
то розв’язок
завжди береться
у вигляді (*), де
 ,
,
тобто у вигляді
функції Бесселя:
 .
.
таким чином,
 ,
,
 .
.
Скористаємося
граничними
умовами. Оскільки
 ;
;
а
 ;
;
то можна записати:
 .
.
Отже,
 —
—
це є умова для
визначення
 .
.
Корені цього
рівняння аналітично
не отримуються,
але їх можна
знайти чисельно:
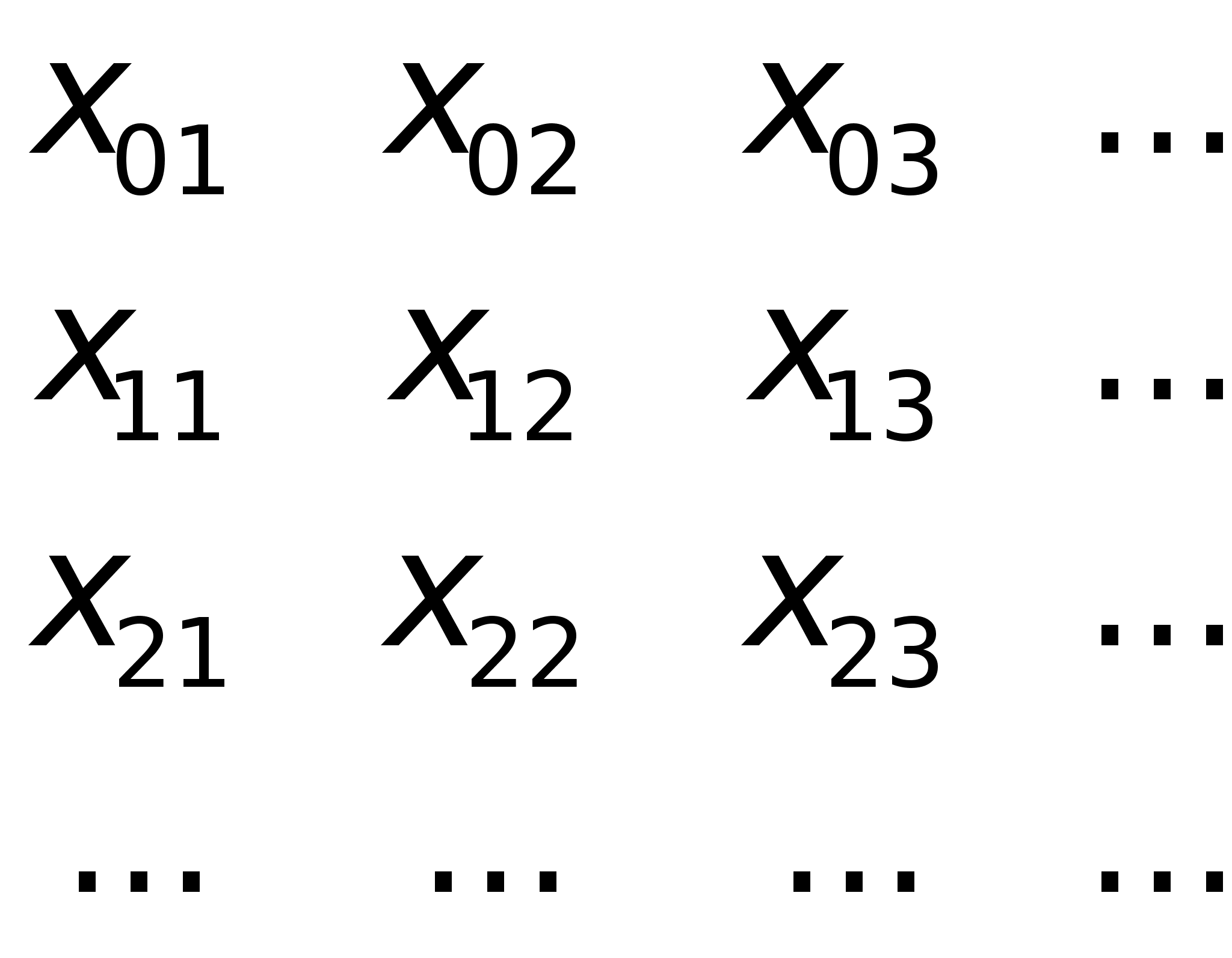
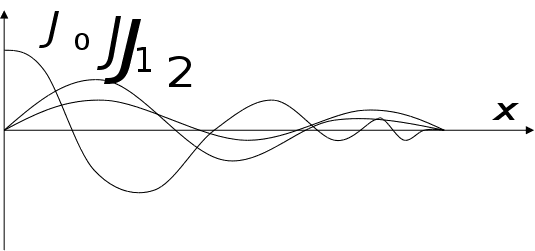
 ,
,
де
 —
—
номер хвилі,
 —
—
номер рядку.
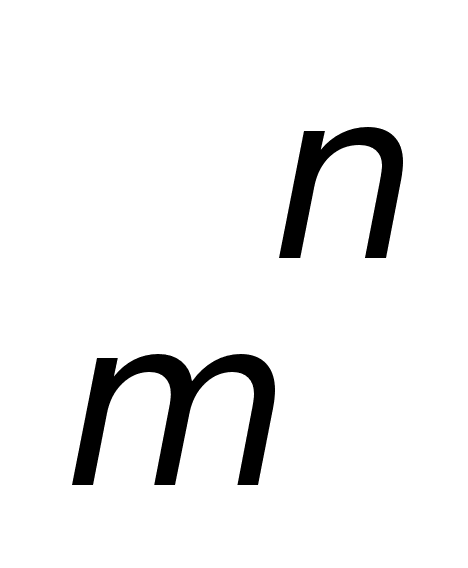
1
2
0
3.83
—
1
1.84
—
Отже,
 .
.
таким чином,
для хвилі
 .
.
Критична довжина
хвилі у хвилеводі
визначається
з умови
 .
.
Аналогічно
 .
.
Тепер знайдемо
картину хвиль.
Для цього
скористаємося
топологічними
перетвореннями:
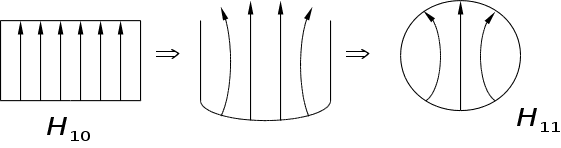
Перетворюючи

в декартову
СК, одержали

в циліндричній
СК.
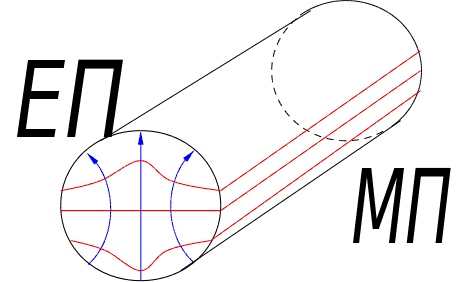
Перший
індекс – змінна
по
 ,
,
другий – змінна
по
 .
.
таким чином
у круглому
хвильоводі
“головною”,
“найкращою”
є хвиля

(в той час як у
квадратному
—
 .
.
Лекція
8
К
 оаксіальна
оаксіальналінія.
тут можуть
розповсюджуватись
хвилі Т (бо тут
можна утворити
конденсатор),
ТЕ, ТМ.
 ,
,
 ,
,
 .
.
 .
.
Розглянемо
хвилю Т. Нам
необхідно
розв’язати
рівняння
 .
.
Зробимо це
методом конформних
відображень.
Його можна
застосувати
для аналітичних
функцій (тих,
що задовольняють
рівнянню Лапласа),
яким і є поле
Т-хвиль.
Для того, щоб
скористатись
методом КВ,
необхідно:
Знайти
відображення,
яке переводить
нашу область,
де існує ЕМ –
поле, у плоский
конденсатор;
Розв’язати
рівняння Лапласа
у плоскому
конденсаторі;
Зворотнім
конформним
перетворенням
знов перейти
в нашу область
– це і буде
розв’язок
задачі:
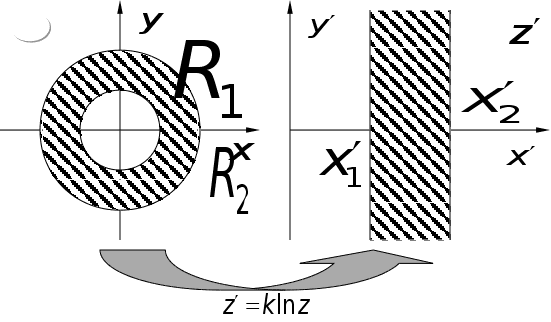
метод конформних
відображень
можна застосувати
для Т – хвилі,
бо вона є розв’язком
рівняння Лапласа:
 ,
,
 .
.
Доведемо, що
відображення

перетворює
циліндричний
конденсатор
в плоский:
 ,
,
 ,
,
тобто
 ,
,
 .
.
Таким чином,
якщо
 .
.
 ,
,
 .
.
Т аким
аким
чином, можна
перетворити
межу циліндричної
області в межу
плоскої. Тому
й область
 перетворюється
перетворюється
в область
 .
.
Розв’язок
задачі в плоскому
конденсаторі: має
має
вигляд:
 .
.
Поклавши

(скориставшись
тим, що потенціал
визначається
з точністю до
константи),
маємо:
 .
.
Скориставшись
зворотнім
перетворенням,
одержимо:
 .
.
Знайдемо
поле:
 ,
,
 .
.
Хвильовий опір:
 .
.
Проте такий
опір не вимірюється.
Більш практичне
означення
хвильового
опору:

— відношення
напруг лінії
до струмів у
цій лінії. Знайдемо

для Т – лінії,
використавши
інтегральні
рівняння Максвела:
 ,
,
тут
 —
—
заряд,
 —
—
ємність на
одиницю довжини.
З урахуванням

можна записати:
 .
.
 .
.
Окрім Т – хвилі,
в коаксіальному
кабелі може
існувати ще
й ТЕ чи ТМ хвиля:
 .
.
Картина хвиль:
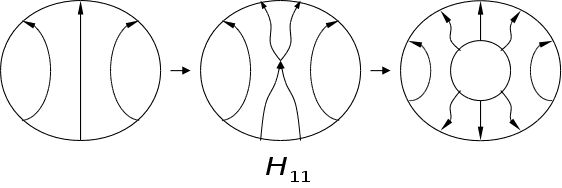
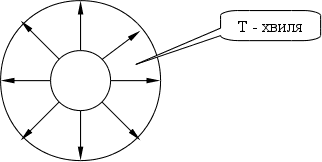
 .
.
Наприклад, для
R1=1мм,
R2=6мм:
 .
.
Лекція
9
Лінії
передач для
інтегральних
схем.
В інтегральній
електроніці
використовуються
в основному
плоскі лінії.
Симетрично
– смушкова
лінія (ССЛ): вона
відкрита, тому
має втрати.

Не симетрично
– смушкова
лінія (НСЛ):

Мікросмушкова
лінія (microstrip
line) – МСЛ. тут
ємність дуже
велика, енергія
сконцентрована.
Підкладка з
діелектрика
 .
.
Лінія двоповерхова
– це не дуже
зручно.

Щілинна лінія
(slot line).
Вона є одноповерховою:
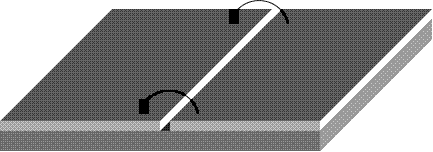
Компланарний
хвильовід –
все в одній
площині.

Поля
в несиметрично
– смушковій
лінії.
Складність
розв’язання
цієї задачі
полягає в тому,
що граничні
умови тут –
нерегулярні;
не можна покласти,
що на поверхні
 .
.
Використовують
наближені
методи; зокрема
конформних
відображень.
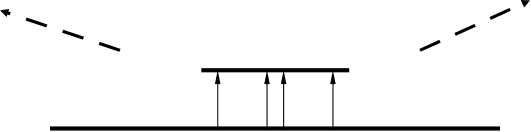
Наближення:
Існує Т – хвиля
(нехтуємо
випромінюванням).
Використаємо
симетрію задачі.
Цікавимося
випромінюванням
на краю.
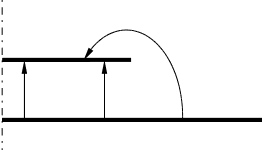

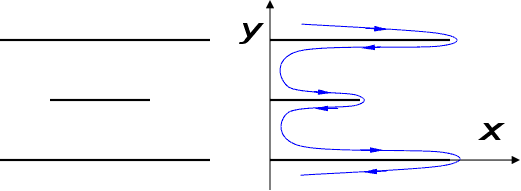
Т реба
реба
розв’язати
задачу: знайти
розв’язок
рівняння Лапласа
у верхній площині
з напівнескінченним
розрізом.
Використаємо
метод конформних
відображень:
тут застосовується
інтегральне
конформне
перетворення
Кристофеля
– Шварца.
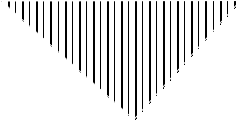
Розглянемо
ламану лінію,
що в точці а
змінює напрямок
на кут
 :
:
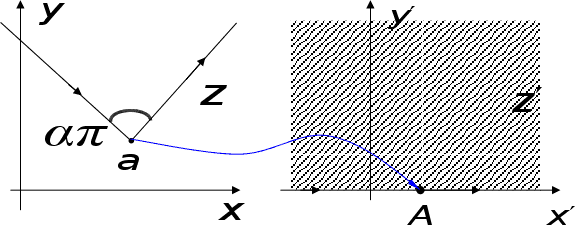
 .
.
Якщо є два зломи,
то
 ,
,
де
 ,
,
 ,
,
 .
.
В нашій конкретній
задачі ламану
можна подати
у вигляді:

К ут
ут
відраховується
проти годинникової
стрілки від
наступного
напрямку до
попереднього.
 ,
,
 ,
,
перенесемо
точки:
 .
.
Проінтегрувавши
отримаємо
шукане перетворення:
 .
.
Константи

та

визначаються
з умов:
 ,
,
отже
 .
.
Умовою

ми не можемо
скористатися,
бо одержимо
 .
.
Використаємо
фізичні міркування:
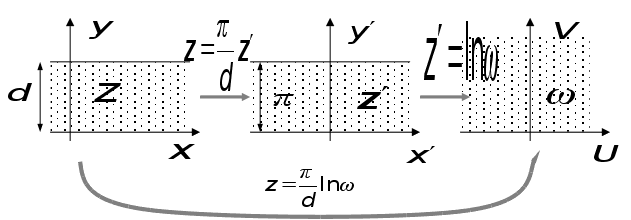
Загальний
вид відображення
 ;
;
бо область
інваріанта
відносно зсуву
вздовж ОХ
(трансляційна
симетрія).
Зрозуміло,
у нашій задачі
область при
 .
.
При
 перетворення
перетворення
набуває вигляду:
 .
.
Порівнюючи
з
 ,
,
 .
.
Отже шукане
перетворення:
 .
.
Для того, щоб
знайти розв’язок
у верхній півплощині,
необхідно
перетворити
її в конденсатор,
використовуючи
перетворення
зворотне до
 :
:
 .
.
Тоді відображення,
що перетворить
вихідну область
( )
)
(край конденсатора)
у конденсатор
( ),
),
має вигляд:
 .
.
Тепер необхідно
розв’язати
рівняння у
плоскому конденсаторі
та скористатись
зворотнім
перетворенням:
 ,
,
 .
.
 .
.
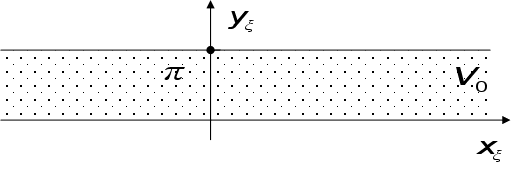
таким чином:
 .
.
Запишемо
рівняння
еквіпотенційних
поверхонь:
 .
.
ЕПП

переходить
в
 .
.
ЕПП

переходить
в
 .
.
Таким чином,
отримаємо таку
картину еквіпотенціальних
поверхонь:
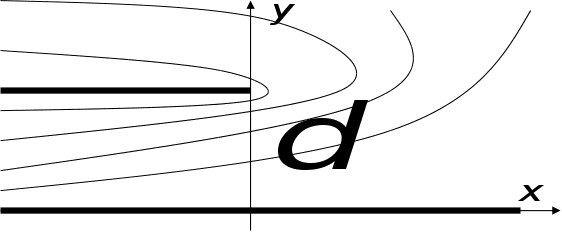
Тепер знайдемо
електричні
силові лінії.
Ці лінії перпендикулярні
ЕПП, однак ми
знайдемо їх
в аналітичний
спосіб. очевидно,
в ( )
)
такі силові
лінії, як на
малюнку. Знайдемо
образ цих ліній
у просторі ( ).
).
Наприклад,
 ,
, .
.
Отримаємо
картину ЕП в
( ):
):
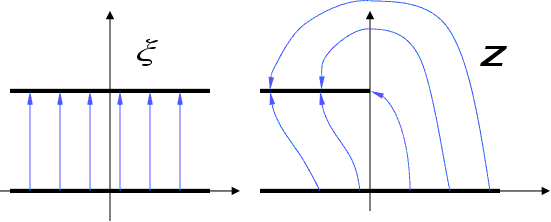
часто важливо
знайти напруженість
поля в певній
точці:
 .
.