Учебная работа. Реферат: Обобщенное золотое сечение и теория времени

Учебная работа. Реферат: Обобщенное золотое сечение и теория времени

Обобщенное Золотое Сечение и Теория времени

В предлагаемой вашему вниманию работе сделана попытка решить одну из частных задач Теории Времени, а именно задачу определения устойчивых скоростей хода времени или, что то же самое, нахождения устойчивых значений плотности времени в данном конкретном причинно-следственном звене посредством применения аппарата структурного анализа [1] к теории времени профессора Н.А.Козырева [2].

Для начала необходимо сделать несколько выводов из Теории Времени Козырева, которые позволят нам применить к ней метод структурного анализа. рассмотрим элементарное причинно-следственное звено. Ключевым подходом к нему у Козырева служило смотреть из нее по направлению на следствие, и против часовой стрелки в следствии, если смотреть на него также из причины. таким образом, Козырев уподоблял ход времени повороту оси вращающегося волчка. однако, если отказаться от таких абстракций и попытаться представить, какой реальный физический процесс может за этим стоять, то самое простое, что приходит в голову — это процесс свертки-развертки пространства, то есть скручивания и возвращения в исходное или близкое к нему состояние. При этом в причине пространство сворачивается, чтобы развернуться в следствии, что полностью соответствует представлениям Козырева о том, что время переносит момент вращения, и что энергия времени поглощается (затрачивается) в причине и выделяется (высвобождается) в следствии. Итак, мы получаем, что движение по часовой стрелке в причине связано со сверткой, сжатием пространства, воздействием причины на следствие и уменьшает плотность времени, а движение против часовой стрелки в следствии связано с разверткой пространства, расширением, воздействием следствия на причину, то есть с обратной связью, и увеличивает плотность времени. Можно также сказать, что время вдыхает жизнь во все в нашем мире.

На самом же деле рассуждения о причине и о следствии являются не более чем данью чисто человеческим представлениям о времени, потому что, по определению, причина — это то, из чего вытекает следствие. Но в реальном причинно-следственном звене не только причина оказывает влияние на следствие, но и следствие оказывает влияние на причину. Поэтому понятия причины и следствия весьма условны и стоит обратной причинной связи, направленной от следствия к причине стать более сильной, сразу же понятия причины и следствия поменяются местами, так как поменяется направление хода времени в причинно-следственном звене.

Теснейшая взаимосвязь между вращательным движением и ходом времени означает, что любое вращательное движение увеличивает или уменьшает плотность времени, а любой ход времени порождает вращательное движение. Одним словом, вращение галактик в метагалактиках, вращение звезд в галактиках, вращение планет вокруг солнц, спутников вокруг планет, также как и собственное вращение тел не только генерирует время, но и является индикатором его хода и неразрывно с ним связано. Поэтому ход времени и движение в пространстве — это одно и тоже. Без движения нет времени, также как без времени нет движения. Не случайно, определенная Козыревым "постоянная" хода времени

км/с

с точностью эксперимента равна абсолютной скорости движения Солнечной системы, которая, согласно [3], сейчас составляет как раз около 400 км/с. очевидно, в общем случае равна абсолютной скорости движения системы, то есть скорости ее движения относительно мирового эфира, первичной материи, абсолютной и неподвижной Вселенной.

Таким образом, время течет совершенно по-разному и не является раз и навсегда заданной константой. Очевидно, суммарная скорость хода времени всей Вселенной как в Едином Целом должна быть равна нулю, то есть должен выполняться закон сохранения времени. Этот же законочевидном виде: суммарная скорость движения всех частиц, составляющих Вселенную равна нулю. При этом не важно, имеет ли Вселенная конечные размеры или же она бесконечна. Главное, чтобы понятие Вселенная означало замкнутую систему, то есть завершенный Абсолют.

Аналогичным образом мы можем рассматривать не только абсолютную скорость движения во времени одной системы, но и измерять относительные скорости движения во времени различных систем. Так, например, имеет смысл говорить о скорости хода времени Земли относительно Солнца, также как о скорости хода времени Солнца относительно центра галактики или скорости хода времени Луны относительно Земли. Все это возможно потому, что Солнечную систему, систему Земля-Луна, галактику в целом, в первом приближении мы вправе считать замкнутыми системами, и, видимо, для таких условно замкнутых систем на коротком промежутке их шкалы времени скорость хода времени относительно центра системы может быть принята за абсолютную.

теперь необходимо кратко изложить принципы структурного анализа [1], дабы применить его к Теории Времени. Структурный анализ рассматривает самоорганизацию систем как процесс стабилизации через резонанс. В основе самоорганизации лежит принцип сохранения универсума, выражающийся в законе сохранения логарифма числа состояний:

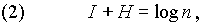
где I
— информация, H
— энтропия, n
— число возможных состояний.

В нормализованном виде этот закон

, где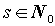

а также

, где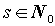

где — энтропия, R
— избыточность, .

системы уравнений (3) и (4) показывают дискретный набор соотношений двух частей Единого Целого, пр и которых будет достигаться состояние динамического равновесия. Значения s
при этом будут показывать количество самоустраняемых дефектов структуры. Преобразуя (3) и (4), получаем соответственно:

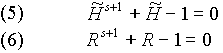
Если рассматривать процесс хода времени как Единое Целое, состоящее из двух противоположностей (причины и следствия, прямой и обратной связи), то, несомненно, мы вправе применить все методы структурного анализа к элементарному причинно-следственному звену, а через него распространить полученные выводы на всю Теорию Времени. поэтому по мере дальнейшего изложения методов структурного анализа, мы сразу будем применять их к Теории Времени.

Так, если причинно-следственная связь в причинно-следственном звене выражается значением , то обратная, следственно-причинная связь выражается значением R
. поэтому, зная значение , характеризующее состояние причинно-следственного звена, мы можем определить отношение фатума и свободы. очевидно, что доля фатума максимальна, когда действует только причинная связь и отсутствует обратная, то есть=1 и R
=0. Когда же прямая и обратная связи равны по силе, то есть =0,5 и R
=0,5, наступает полный хаос, полная свобода. Таким образом, доля фатума в причинно-следственном звене может быть выражена как

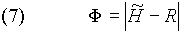
А доля свободы соответственно как

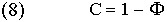
Таким образом, мы получаем возможность, определив порядок состояния динамического равновесия системы s
, вычислить соотношение прямой и обратной связей и и определить долю фатума и свободы , присутствующих в ней.

очевидно, решения уравнений (5) и (6) существуют при любых s
, однако для начала ограничимся рассмотрением при 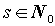. значения для s
от 0 до 31 приведены в таблице 1 и в графическом виде на рисунке 1.

Таблица 1

s

s

0
0,50000000000
16
0,88191004828

1
0,61803398875
17
0,88624516859

2
0,68232780383
18
0,89022556753

3
0,72449195900
19
0,89389541191

4
0,75487766625
20
0,89729162218

5
0,77808959868
21
0,90044532576

6
0,79654435413
22
0,90338297001

7
0,81165232003
23
0,90612718508

8
0,82430056323
24
0,90869746041

9
0,83507904272
25
0,91111068059

10
0,84439752879
26
0,91338155389

11
0,85255071449
27
0,91552295788

12
0,85975667169
28
0,91754622045

13
0,86618067237
29
0,91946135001

14
0,87195053878
30
0,92127722540

15
0,87716686945
31
0,92300175350

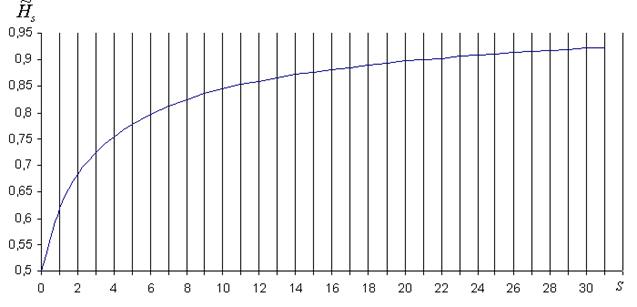
рис. 1

Как видно из таблицы 1, , то есть при нулевом значении s
достигается полное равновесие между двумя частями Единого Целого, то есть состояние полной свободы. При s
=1 значение равно обыкновенному Золотому Сечению:

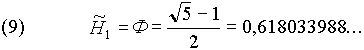
Поэтому соотношения (5) и (6) получили название Обобщенного Золотого Сечения (ОЗС). Мы не будем вдаваться в философско-мировоззренческий смысл Золотого Сечения, который подробно освещен в большом количестве работ [см. например 1, 7, 8]. Отметим лишь тот факт, что исторически оно имеет огромное значение в изучении свойств живой (самоорганизующейся) материи.

дальнейшее развитие идеи ОЗС приводит нас к построению функции

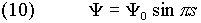
Выражая s
через R
и и используя (3), получаем

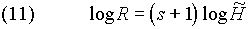
Подставляя полученное выражение для s
в (10), находим окончательный вид функции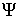

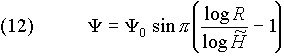
где .

Итак, мы построили такую функцию 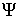, что ее нули представляют собой наиболее гармоничные, равновесные состояния. Теперь необходимо определить границы качественных переходов, то есть точки максимальной дисгармонии системы, когда никакое равновесие невозможно. Очевидно, такими точками будут являться экстремумы функции 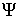. Из этого следует, что ряд при 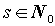является структурной дисгармонии. Он будет определять "зеркальные грани", переход через которые будет означать резкую перемену качества, смену структурно-функционального состояния. В рамках данной работы в виду ее ограниченного объема не имеет особого смысла подробно рассматривать этот ряд, однако без его упоминания описание методов структурного анализа выглядело бы незаконченным.

Теперь, прежде чем перейти к рассмотрению Солнечной системы, приведем некоторые интересные статистические данные, касающиеся нашей планеты [4].

Таблица 2

Полушарие

Северное полушарие

Южное полушарие

Всего на Земле

Суша
100*
39%
49*
19%
149*
29%

Вода
155*
61%
206*
81%
361*
71%

Всего
255*
100%
255*
100%
510*
100%

* миллионы квадратных километров

Итак, пропорция воды и суши в северном полушарии Земли с точностью до процента равна значению при s
=1, в южном — значению при s
=7, а в целом по Земле — значению при s
=3. очевидно, такое различие обусловлено разностью скорости хода времени в северном и южном полушариях, возникающей из-за собственного вращения Земли, увеличивающего плотность времени в северном и уменьшающего ее в южном полушарии. таким образом, процессы эволюции должны происходить быстрее в северном полушарии, чем в южном, как это доказано в [6] на основании разницы в величине ускорения свободного падения на полюсах. Таким образом, Обобщенное Золотое Сечение — это не просто математическая абстракция, а вполне реальная функция, которая может и должна быть применена для анализа строения Мироздания, как двойственной системы, состоящей, какой бы уровень мы ни взяли, из двух противоположностей.

Обратим внимание на то, что для Земли в целом распределение воды и суши оказалось равным третьему "порогу" ОЗС (s
=3). В то же время Земля — третья планета от Солнца. именно при сопоставлении этих двух фактов и возникла основная идея данной работы. Не означает ли такое совпадение, что устойчивые (под устойчивостью в данном случае понимается состояние динамического равновесия всей Солнечной системы в целом) орбиты планет определяются рядом Обобщенных Золотых Сечений как устойчивые орбитали "атома" Солнечной системы, как устойчивые скорости хода времени планет относительно Солнца?

чтобы попытаться найти ответ на этот вопрос, Автором была построена кривая, где по оси абсцисс были отложены значения , а по оси ординат — большие полуоси главных планет Солнечной системы (рис.2). И выяснилось, что эта кривая отлично описывается обыкновенной гиперболой!

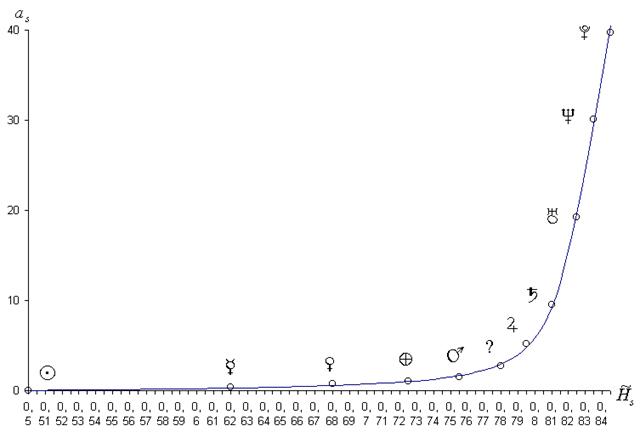
рис. 2

В [1] в качестве целевой функции для поиска реальных физических параметров системы, определяющих ее динамическое равновесие, предлагается брать функцию вида:

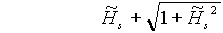
или более сложную, например,

или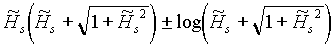

Однако, после непродолжительных экспериментов стало очевидно, что наиболее хорошее приближение получается, если за основу взять обобщение гиперболы

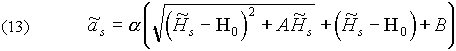
где 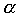, , 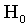A
и B
— неизвестные коэффициенты, которые требуется найти.

При этом коэффициент 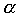определяет масштаб и выражается в астрономических единицах, 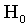определяет расположение фокуса гиперболы, A
— ее кривизну, B
— начальное смещение при s
=0, поскольку в ходе исследований выяснилось, что не удается добиться хорошей аппроксимации, если зафиксировать значение равным нулю. Это объясняется тем, что само Солнце за счет своего собственного вращения, ненулевых размеров и возмущений от планет имеет ненулевую скорость хода времени относительно центра Солнечной системы.

Функция (13) является "фильтром", отделяющим идеальную пропорцию ОЗС от реальности. Если такая характеристика как соотношение площадей воды и суши на поверхности Земли оказалась зависящей от ОЗС по линейному закону, то большие полуоси планет оказались гиперболической функцией от ОЗС. объяснять этот факт можно различными путями, однако близость данной зависимости к гиперболе очевидна и может быть принята за рабочую гипотезу.

В качестве исходных данных для аппроксимации были взяты большие полуоси главных планет на 27 июня 1992 года [5]. Для пояса астероидов (по одной из гипотез здесь была орбита разрушенной планеты
Фаэтон) была взята большая полуось орбиты астероида Церера [5] и весовой коэффициент 0,5. Для Солнца "период обращения" был приравнен к периоду его собственного вращения (около 25 часов). Решение искалось методом наименьших квадратов и были получены следующие значения коэффициентов:

=
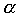
622,70482193

=
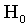
0,8154296084

A

=
0,0004920468

B

=
-0,0003427966

Результаты вычислений по формуле (13) при этих коэффициентах приведены в таблице 3 и на рисунке 3.

Таблица 3

s

название

, а.е.

, год
идеальный цикл

, а.е.

, год
реальный цикл

, %

0

солнце

0,0292323
0,0049980

[0,0201477]
[0,0028520
]
[-36,79
]

1

Меркурий

0,2652667
0,1366231

0,3870972
0,2408408

37,35

2

Венера

0,5682112
0,4283164

0,7233286
0,6151817

24,02

3

Земля

0,9941917
0,9913002

0,9999846
0,9999769

0,58

4

Марс

1,6503591
2,1201553

1,5236959
1,8808209

—7,98

5

Фаэтон

2,7855127
4,6489803

[2,7688824]
[4,6074090
]
[-0,60
]

6

Юпитер

5,0640356
11,395808

5,2031024
11,868438

2,71

7

Сатурн

10,099045
32,093748

9,5219707
29,382603

—5,88

8

Уран

19,014111
82,911361

19,201051
84,137093

0,98

9

Нептун

29,602015
161,05785

30,073664
164,92235

1,58

10

Плутон

39,881622
251,86001

39,724908
250,37695

—0,39

11

Сома

49,302596
346,18216

?
?
?

12

Дхарма

57,818584
439,64402

?
?
?

13

Род

65,507058
530,19075

?
?
?

14

Тот

72,467239
616,89688

?
?
?

15

Аредвисура

78,793033
699,40983

?
?
?

16

Митра

84,566649
777,67597

?
?
?

17

?
89,858233
851,79838

?
?
?

18

?
94,727183
921,95969

?
?
?

19

?
99,223783
988,37936

?
?
?

20

?
103,39073
1051,2896

?
?
?

21

?
107,26442
1110,9219

?
?
?

22

?
110,87607
1167,4996

?
?
?

23

?
114,25255
1221,2338

?
?
?

представляют собой относительное различие между вычисленными (идеальными) и реальными значениями больших полуосей:

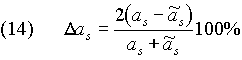
Наибольшие отклонения получились для Солнца, Меркурия и Венеры, то есть для тел, расположенных в непосредственной близости к центру системы. По видимому, это объясняется тем, что Солнце, являясь генератором времени, искривляет время вокруг себя, что особенно заметно на малом расстоянии. Погрешности для остальных планет являются доказательством того, что они находится не точно на устойчивых орбитах, а в их окрестности.

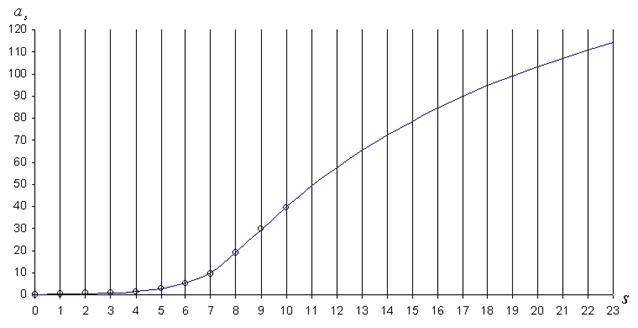
рис. 3

Из таблицы 3 и рисунка 3 видно, что, если гипотеза о связи ОЗС со значениями больших полуосей верна, за Плутоном должны существовать планеты с циклами около 346, 440, 530, 617, 699, 777 и так далее лет. Конечно, не на всех устойчивых орбитах обязательно существуют планеты, но опыт с Фаэтоном
показывает, что свято место пусто не бывает и даже если там нет одной большой планеты, там должно находиться эквивалентное по массе количество малых тел. Автор взял на себя риск, исходя из мифологии, предложить имя одной из дальних (высших) планет. кроме того, опираясь на некоторые данные, почерпнутые из древних текстов, можно предположить, что эклиптическая долгота планеты с циклом 440 лет, которую предлагается назвать Дхарма
(в буддизме
Дхарма
— это общий универсальный мистериальный принцип взаимосвязи всех законов и явлений в мироздании, законзаконгода составляет примерно 43 градуса.

Обратим внимание, что фокус гиперболы лежит между значениями s
=7 и s
=8, то есть между Сатурном и Ураном, как раз на грани между планетами, видимыми невооруженным глазом, и планетами дальними, открытыми лишь относительно недавно. Кроме того, вблизи этой точки перегиба находится замечательный астероид Хирон (2060), который больше похож на планетоид, чем на осколок разрушенного небесного тела, как большинство других астероидов. Еще более интересно, что самая большая планета Солнечной системы — Юпитер, который иногда называют несостоявшейся звездой — попала почти точно в точку перегиба гиперболы (рис.2)! Не потому ли Юпитер "набрал" самый большой вес, что его орбита находится как раз на этом перегибе?

Из (13) также следует, что а.е.,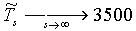

следующим этапом нашего анализа будет рассмотрение систем спутников планет, имеющее своей целью подтвердить или опровергнуть гипотезу о связи ОЗС с большими полуосями через функцию (13).

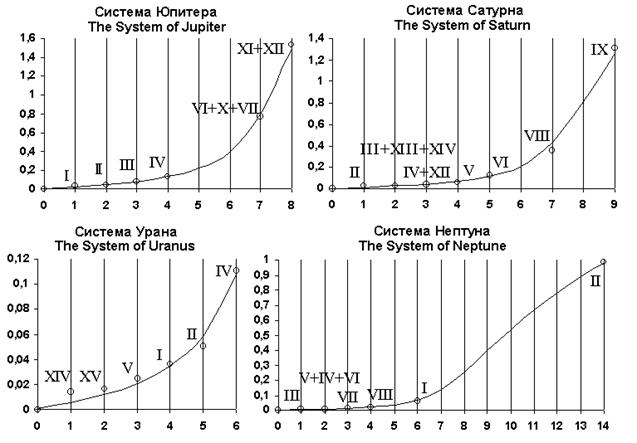
рис. 4

Наибольший Интерес представляют системы спутников Юпитера, Сатурна, Урана и Нептуна. Скажем несколько слов о том, как проводился анализ. В первую очередь из рассмотрения пришлось исключить часть тел, имеющих неправильную форму, так как в большинстве своем они явно не укладывались ни в какую гладкую аппроксимацию. Также пришлось исключить из рассмотрения несколько весьма незначительных по размерам ближайших спутников в системах Юпитера, Сатурна и Урана. предварительный анализ показал, что все системы спутников планет Солнечной системы хорошо аппроксимируются зависимостью (13), умноженной на поправочный коэффициент 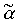уникальный для каждой конкретной системы. Результаты этой аппроксимации для систем спутников Юпитера, Сатурна, Урана и Нептуна приведены на рисунке 4 (по оси абсцисс отложены значения s, по оси ординат — значения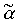 ). Значения поправочных коэффициентов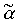 даны в таблице 4 и в виде графика на рисунке 5.

Приведенные на рисунке 4 графики позволяют сделать заключение, что общий вид и даже все параметры формулы (13) остаются практически без изменений в пределах всей Солнечной системы.

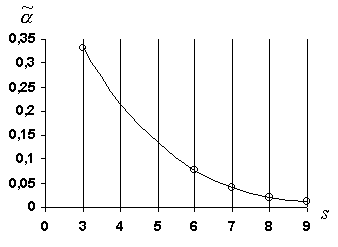
рис. 5

Таблица 4

s

планета

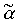
3

Земля
0,3315

6

Юпитер
0,0783

7

Сатурн
0,0428

8

Уран
0,0212

9

Нептун
0,0135

Из рисунка 5 и данных таблицы 4 очевидно, что коэффициент 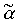зависитобратно пропорционально от большой полуоси :

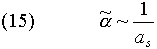
То есть чем дальше от Солнца находится система, тем более она "сжата", тем стремительнее уменьшаются большие полуоси устойчивых орбит спутников при тех же значениях s
. противоположная картина наблюдается при приближении к Солнцу: здесь устойчивые орбиты спутников стремительно "раздуваются" и поэтому, к примеру, у Меркурия вообще не может быть спутников, так как первая ближайшая к нему устойчивая орбита спутника настолько велика, что любое тело, помещенное на нее, либо упадет на Солнце, либо переместиться на околосолнечную орбиту и станет еще одной малой планетой.

Отдельного рассмотрения заслуживает система спутников нашей с вами планеты — Земли. Коэффициент 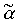=0,3315 был выбран исключительно из того предположения, что идеальный цикл Луны должен составлять около 30 земных суток и Луна находится на орбите вокруг Земли соответствующей ОЗС при s
=2.

Цикл в 30 земных суток был выбран отнюдь не вследствие округления. Ведь градусная мера содержит в себе ровно 360 градусов, а древние календари — 12 месяцев по 30 дней. Такое совпадение не может быть случайным. наиболее убедительным его объяснением является то, что идеальный (доисторический) цикл Луны составлял ровно 30 земных суток, а земной год длился ровно 360 земных дней (идеальный цикл Земли в таблице 3 получился равным 362 дня, что подтверждает эту гипотезу). Конечно, и сутки на Земле тогда должны были быть другими, но точную их продолжительность в те далекие времена установить пока не представляется возможным.

Соответствие орбиты Луны значению s
=2 было принято, чтобы сохранить гладкость кривой на рисунке 5. При этом цикл первой устойчивой орбиты спутника Земли составил 9,5 дней, а третьей — 69 дней.

Система спутников Марса оказалась не подлежащей никакому анализу, так как оба его спутника являются телами неправильной формы и скорее всего это просто случайно захваченные Марсом астероиды, находящиеся вдали от устойчивых орбит. попытки поместить один из спутников Марса на устойчивую орбиту приводили к потере гладкости кривой на рисунке 5.

Исходя из построенной аппроксимации, теоретически можно предположить существование спутника Венеры. К примеру, если принять для Венеры 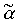=0,55, то период обращения спутника по первой устойчивой орбите вокруг Венеры составит около 20 земных суток, а по второй — около 64 суток.

Итак, сделаем несколько заключительных выводов из всего вышеизложенного.

Ход времени и движение в пространстве неразрывно связаны друг с другом и по сути представляют собой один процесс.

"постоянная" хода времени Козырева на самом деле равна абсолютной скорости движения системы, то есть скорости ее движения относительно фонового излучения Вселенной.

Для систем, которые на коротком промежутке времени можно считать замкнутыми, скорость хода времени относительно центра этой системы на протяжение короткого промежутка времени может быть принята за абсолютную.

Обобщенное Золотое Сечение (ОЗС) является универсальным ключом к анализу состояний динамического равновесия и может быть и должно быть применено для рассмотрения процесса хода времени, как процесса динамического равновесия свертки-развертки пространства.

Дискретный набор устойчивых соотношений прямой и обратной связи в причинно-следственном звене определяется по закону ОЗС.

Главные планеты Солнечной системы, также как и их спутники находятся вблизи устойчивых орбит, определяемых по закону ОЗС.

При удалении от центра Солнечной системы, системы спутников планет испытывают сжатие, которое выражается в уменьшении больших полуосей спутников для одного и того же "порога" ОЗС. Это происходит из-за возрастания расстояния до генератора времени — Солнца — и, вследствие этого, уменьшения плотности времени. Причем уменьшение плотности происходит обратно пропорционально расстоянию.

Так как классическое Золотое Сечение является, согласно большинству исследований, свойством живой материи, из этого следует, что Земля, Солнечная система и Вселенная в целом есть живой организм, живая самоорганизующаяся система, Самосознающий Воплощенный Абсолют.

Литература

Сороко Э. М. Структурная гармония систем. Минск: Наука и техника, 1984. 264 с.

Козырев Н. А. Избранные труды. Л.: Издательство Ленинградского университета, 1991. 448 с.

Шпитальная А. А., Заколдаев Ю. А., Ефимов А. А. Проблема времени в геологии и звездной астрономии // Серия "проблемы исследования Вселенной" Выпуск 15. проблемы пространства и времени в современном естествознании. С.-Петербург, 1991. с.95-106.

Малый Атлас Мира, главное управление геодезии и картографии при Совете Министров СССР. Москва: 1981.

Эфемериды малых планет на 1993 год. С.-Петербург: ИТА, 1992.

Бутусов К. П. время — физическая субстанция // Серия "проблемы исследования Вселенной" Выпуск 15. проблемы пространства и времени в современном естествознании. С.-Петербург, 1991. с.301-310.

Васютинский Н. А. Золотая пропорция. Москва: молодая гвардия, 1990.

Стахов А. П. Коды золотой пропорции. Москва: Радио и связь, 1984.