Учебная работа. Реферат: Курсовая работа по теории электрических цепей

(Пока оценок нет)

Загрузка...

Учебная работа. Реферат: Курсовая работа по теории электрических цепей

часть 1.

Анализ цепи во временной области методом переменных состояния при постоянных воздействиях.

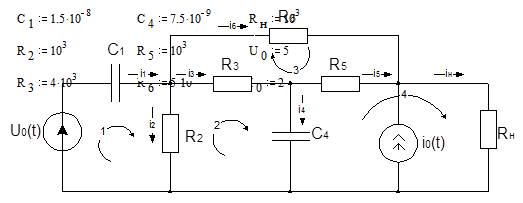
Дано:

Для схемы:

U0
(t)= U0
=constU0
=5 В

i0
(t)=I0
d1
(t) I0
=2 A

1.1
Составить уравнения состояния для цепи при
t
³
0.

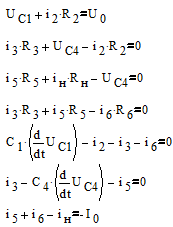Переменными состояния для данной схемы будут являться напряжения на емкостях С1
и С4
. Для нахождения уравнений состояния запишем уравнения по I и II законам Кирхгофа:

(1)

Для нахождения производных переменных состояния решим следующую систему, полученную из системы (1), приняв за неизвестные все токи, участвующие в системе (1) и первые производные переменных состояния. Переменные состояния примем за известные величины для получения их в правой части уравнений состояния:

(2)

Решаем эту систему в матричном виде с помощью MathCad:

таким образом, уравнения состояния будут иметь вид:

1.2 найти точные решения уравнений состояния.

Сначала найдем корни характеристического уравнения как собственные числа матрицы, составленной из коэффициентов при переменных состояния в уравнениях состояния:

Общий вид точных решений уравнений состояния:

Вынужденные составляющие найдем как частное решение уравнений состояния, учитывая то, что если в цепи включены только постоянные источники питания, значит, и принужденные составляющие будут константами, соответственно производные принужденных составляющих будут равны нулю. Учитывая выше сказанное, найдем их из уравнений состояния следующим способом:

Начальные условия (находятся из схемы):

Для нахождения постоянных интегрирования A1
, A2
, A3
, A4
требуется 4 уравнения. первые два уравнения получим из выражений точного решения уравнений состояния, учитывая законы коммутаций: переменные состояния не меняют своего значения в момент коммутации.

При t=0:

Далее найдем значения производных переменных состояния при t=0 из уравнений состояния:

Выражения эти производных найденные из выражений решения уравнений состояния:

При t=0:

таким образом имеем 4 уравнения для нахождения постоянных интегрирования, находим их:

Точные решения уравнений состояния:

1.2
найти решения уравнений состояния, используя один из численных методов.

Для численного решения уравнений состояния воспользуемся алгоритмом Эйлера:

Подставляя выражения производных из уравнений состояния:

h – шаг расчета =2*10-6
с. i=1…100. Переменными с нулевыми индексами являются значения начальных условий.

1.2.2 Найти точные решения уравнений состояния.(второй способ)

e(A)t
= a0
+ a1
(A) e(A)t
=

(X) = [e(A)t
-1][A]-1
[B][V]

1.4 построить точные и численные решения уравнений состояния, совместив их попарно на одном графике для каждой из переменной состояния.

часть 2.

Анализ цепи операторным методом при апериодическом воздействии.

Анализу подлежит следующая цепь:

Параметры импульса: Um
=10 В tu
=6*10-5
c

Форма импульса:

2.1 определить функцию передачи:

воспользуемся методом пропорциональных величин и определим u(t)=1(t), его Лапласово изображение U0
(s)=1/s.

Запишем уравнения по законам Кирхгофа в операторной форме, учитывая, что начальные условия нулевые:

Решаем эту систему:

таким образом:

Функция передачи:

2.2 Найти нули и полюсы функции передачи и нанести их на плоскость комплексной частоты.
Полюсы:

Нули:

Плоскость комплексной частоты:

2.3 найти переходную и импульсную характеристики для выходного напряжения.

Импульсная характеристика:

Выделим постоянную часть в HU
(s):

Числитель получившейся дроби:

упрощенное выражение HU
(s):

Для нахождения оригинала воспользуемся теоремой о разложении. Для этого найдем производную знаменателя:

Коэффициенты разложения:

Оригинал импульсной характеристики:

Переходная характеристика:

Этим же методом находим оригинал характеристики:

2.4 Определить изображение по Лапласу входного импульса.

Изабражение по Лапласу фукции f(t):

Входной импульс представляет собой функцию

поэтому изображение входного сигнала будет

2.5 Найти напряжение на выходе схемы, используя
HU

(
s
).

Изображение выходного сигнала:

Найдем отдельно оригиналы части выражения при и при части, не имеющей этого множителя:

Для части выражения при ,используя теорему о разложении:

Для части выражения не имеющей множителя ,используя теорему о разложении:

Функция напряжения на выходе схемы, получена с использованием теоремы о смещении оригинала:

2.6 Построить на одном графике переходную и импульсную характеристики цепи, на другом – входной и выходной сигналы.

Переходная h1
(t) и импульсная h(t) характеристики.

Входной и выходной сигналы.

Часть 3.

Анализ цепи частотным методом при апериодическом воздействии.

3.1 Найти и построить амплитудно-фазовую (АФХ), амлитудно-частотную (АЧХ) и фазо-частотную (ФЧХ) характеристики функций передачи HU
(s).

амплитудно-фазовая характеристика:

амплитудно-частотная характеристика:

фазо-частотная характеристика:

График АЧХ:

График ФЧХ:

3.2 определить полосу пропускания цепи по уровню 0.707

.

Из графика АЧХ находим полосу пропускания цепи: с-1
.

3.3 найти и построить амплитудный и фазовый спектры входного сигнала по уровню 0.1

.

Амплитудный спектр входного сигнала:

Фазовый спектр входного сигнала:

График амплитудного и фазового спектра входного сигнала:

Ширина спектра с-1
.

3.4 Сопоставляя спектры входного сигнала с частотными характеристиками цепи, дать предварительные заключения об ожидаемых искажениях сигнала на выходе цепи.

существенная часть амплитудного спектра входного сигнала укладывается в полосу пропускания, исключая полосу 0-5*104
с-1
, где и будут наблюдаться основные амплитудные искажения. Фазо-частотная характеристика цепи нелинейна, поэтому здесь будут иметь место фазовые искажения, что видно на рис.

3.5 Найти и построить амплитудный и фазовый спектр выходного сигнала.

Получаются по формулам:

3.6 определить выходной сигнал по вещественной частотной характеристике, используя приближенный метод Гиллемина.

Вещественная характеристика:

Существенную часть этой характеристики кусочно-линейно аппроксимируем. Начертим первую и вторую производную кусочно-линейной аппроксимирующей функции.

График вещественной характеристики:

Тогда:

График напряжения, вычисленного по этой формуле, и полученный в ч.2.

Часть 4.

Анализ цепи частотным методом при периодическом воздействии.

Дано: T=18*10-5
c. Um
=10 В. tu
=6*10-5
c.

форма сигнала u0
(t):

4.1 Разложить в ряд Фурье заданную периодическую последовательность импульсов и построить ее амплитудный и фазовый спектры.

Коэффициенты ряда Фурье для u0
(t) найдём из следующего соотношения:

где w1
= 2p/Т , k=0, 1, 2, … w1=
3.491*104
с.

значения Ak
и ak
приведены в табл. ,на рис. , построены соответственно амплитудный и фазовый спектры заданной периодически последовательности сигналов u0
(t).

k
Ak

0
0
0

1
2.067
0.524

2
3.308
-0.524

3
2.774
-1.571

4
2.363
-2.618

5
1.034
2.618

6
0
1.571

7
0.413
-2.618

8
0.301
2.618

9
0
1.571

таким образом, в соответствии с шириной спектра .

4.2 Построить на одном графике заданную периодическую последовательность импульсов и ее аппроксимацию отрезком ряда Фурье, число гармоник которого определяется шириной амплитудного спектра входного сигнала, найденной в п 3.3.

4.3 Используя рассчитанные в п. 3.1 АЧХ и ФЧХ функции передачи цепи, определить напряжение или ток на выходе цепи в виде отрезка ряда Фурье.