Учебная работа. Реферат: Эффект Холла

Учебная работа. Реферат: Эффект Холла

САНКТ-ПЕТЕРБУРГСКИЙ государственный МОРСКОЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра физики

Реферат

на тему

Эффект Холла

Выполнил:

студент группы 32СУ1

Лазарев Герасим

Проверил:

преподаватель Скидан В.В.

2000

Содержание.

Общие сведения

Объяснение эффекта Холла с помощью электронной теории

Эффект Холла в ферромагнетиках

Эффект Холла в полупроводниках

Эффект Холла на инерционных электронах в полупроводниках

Датчик ЭДС Холла

список используемой литературы

1.Общие сведения.

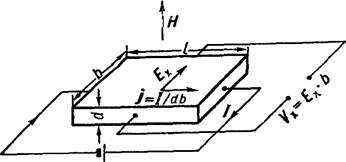Эффектом Холла называется появление в провод­нике с током плотностью j
, помещён­ном в магнитное поле Н
, электрического поля Ех

, перпендикулярного Н
и j
. При этом на­пряжённость электрического поля, называемого ещё полем Холла, равна:

Рис 1.1

Ex
= RHj sin
a
, (1)

где a угол между векторами Н
и J
(a
<180°
). Когда H
^
j
, то величина поля Холла Ех

максимальна: Ex
= RHj
. Ве­личина R
, называемая коэффициентом Холла, является основной характеристикой эффекта Холла. Эффект открыт Эдвином Гербертом Холлом в 1879 в тонких пла­стинках золота. Для наблюдения Холла эффекта вдоль прямоугольных пластин из иссле­дуемых веществ, длина которых l
значитель­но больше ширины b
и толщины d
, про­пускается ток:

I = jbd
(см. рис.);

здесь маг­нитное поле перпендикулярно плоскос­ти пластинки. На середине боковых граней, перпендикулярно току, распо­ложены электроды, между которыми из­меряется ЭДС Холла Vx

:

Vx
= Ех
b = RHj
/
d. (2)

Так как ЭДС Холла меняет знак на обратный при изменении направления магнитного поля на обратное, то Холла эффект относится к не­чётным гальваномагнитным явлениям.

простейшая теория Холла эффекта объясняет появление ЭДС Холла взаимодействием носителей тока (электронов проводимости и дырок) с магнитным полем. Под дейст­вием электрического поля носители заряда приобретают направленное движе­ние (дрейф), средняя скорость которого (дрейфовая скорость) vдр

¹
0
. Плотность тока в проводнике j = n*evдр

, где n
— концентрация чи­сла носителей, е
— их заряд. При наложе­нии магнитного поля на носители действу­ет Лоренца сила: F = e[Hvдp
]
, под действием которой частицы отклоняются в направлении, перпендикулярном vдр

и Н
. В результате в обеих гранях провод­ника конечных размеров происходит на­копление заряда и возникает электростатическое поле — поле Холла. В свою очередь поле Холла действует на заряды и урав­новешивает силу Лоренца. В условиях равновесия eEx
= еНvдр

, Ex
=1/ne Hj
, отсюда R = 1/ne
(cмз
/кулон). знак R
сов­падает со знаком носителей тока. Для металлов, у которых концентрация носи­телей (электронов проводимости) близка к плотности атомов (n
»1022
См-3
), R
~10-3
(см3
/кулон), у полупроводников кон­центрация носителей значительно меньше и R
~105
(см3
/кулон). Коэффициент Холла R
мо­жет быть выражен через подвижность носителей заряда m
= е
t
/m*
и удельную электропроводность s
= j/E = еnvлр
/Е
:

R=
m
/
s
(3)

здесь m*
— эффективная масса носи­телей, t
— среднее время между двумя последовательными соударениями с рассеивающи­ми центрами.

иногда при описании Холла эффекта вводят угол Холла j
между током j
и направлением суммарного поля Е
: tg
j
= Ex
/E=
W
t
, где W
— циклотронная частота носи­телей заряда. В слабых полях (
W
t
<<1)
угол Холла j
»
W
t
, можно рассматривать как угол, на который отклоняется движу­щийся заряд за время t
. Приведённая те­ория справедлива для изотропного про­водника (в частности, для поликристал­ла), у которого m*
и t
их— постоянные вели­чины. Коэффициент Холла (для изотроп­ных полупроводников) выражается через парциальные проводимости s
э

и s
д

и концентрации электронов nэ

и дырок nд

:

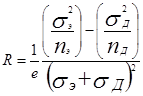(a) для слабых полей

(4)

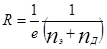(б) для сильных полей.

При nэ
= nд
, = n
для всей области магнитных полей :

,

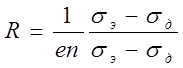а знак R
указывает на преобладающий тип про­водимости.

Для металлов величина R
зависит от зонной структуры и формы Ферми поверхности. В случае замкнутых по­верхностей Ферми и в сильных магнит­ных полях (
W
t
»1)
коэффициент Холла изо­тропен, а выражения для R
совпадают с формулой 4,б. Для открытых поверхно­стей Ферми коэффициент R
анизотропен. Одна­ко, если направление Н
относительно кристаллографических осей выбрано так, что не возникает открытых сечений поверхности Ферми, то выражение для R
аналогич­но 4,б.

2. объяснение эффекта Холла с помощью электронной теории.

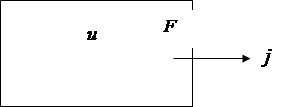
Если металлическую пластинку, вдоль которой течет постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлениям тока и поля возникает разность потенциалов U=j1
-j2
(смотри рис 2.1). Она называется Холловской разностью потенциалов (в предыдущем пункте – ЭДС Холла) и определяется выражением:

uh

=RbjB (2.1)

здесь b
— ширина пластинки, j
— плотность тока, B
— магнитная индукция поля, R
— коэффициент пропорциональности, получивший название постоянной Холла. Эффект Холла очень просто объясняется электронной теорией, отсутствие магнитного поля ток в пластинке обусловливается электрическим полем Ео

(смотри рис 2.2). Эквипотенциальные поверхности этого поля образуют систему перпендикулярных к вектору Ео

скоростей. Две из них изображены на рисунке сплошными прямыми линиями. Потенциал во всех точках каждой поверхности, а следовательно, и в точках 1 и 2 одинаков. Носители тока — электроны — имеют отрицательный заряд, поэтому скорость их упорядоченного движения и направлена противоположно вектору плотности тока j
.

При включении магнитного поля каждый носитель оказывается под действием магнитной силы F
, направленной вдоль стороны b
пластинки и равной по модулю

F=euB (2.2)

В результате у электронов появляется составляющая скорости, направленная к верхней (на рисунке) грани пластинки. У этой грани образуется избыток отрицательных, соответственно у нижней грани — избыток положительных зарядов. Следовательно, возникает дополнительное поперечное электрическое поле ЕB

. Тогда напряженность этого поля достигает такого значения, что его действие на заряды будет уравновешивать силу (2.2), установится стационарное распределение зарядов в поперечном направлении. соответствующее значение EB

определяется условием: eEB
=euB
. Отсюда:

ЕB
=uВ.

Поле ЕB

складывается с полем Ео

в результирующее поле E
. Эквипотенциальные поверхности перпендикулярны к вектору напряженности поля. Следовательно, они повернутся и займут положение, изображенное на рис. 2.2 пунктиром. Точки 1 и 2, которые прежде лежали на одной и той же эквипотенциальной поверхности, теперь имеют разные потенциалы. Чтобы найти напряжение воз­никающее между этими точками, нужно умножить расстояние между ними b
на напряженность ЕB

:

UH=bEB
=buB

Выразим u
через j
, n
и e
в соответствии с формулой j=neu
. В результате получим:

UH
=(1/ne)bjB (2.3)

Последнее выражение совпадает с (2.1), если положить

R=1/ne (2.4)

Из (2.4) следует, что, измерив постоянную Холла, можно найти концентрацию носителей тока в данном металле (т. е. число носи­телей в единице объема).

Важной характеристикой вещества является подвижность в нем носителей тока. Подвижностью носителей тока называется средняя скорость, приобретаемая носителями при напряженности электри­ческого поля, равной единице. Если в поле напряженности Е
носи­тели приобретают скорость u
то подвижность их u0

равна:

U0
=u/E (2.5)

Подвижность можно связать с проводимостьюs
и концентрацией носителей n
. Для этого разделим соотношение j=neu
на напряжённость поля Е
. Приняв во внимание, что отношение j
к Е
дает s
, а отношение u
к Е
— подвижность, получим:

s
=neu0
(2.6)

Измерив постоянную Холла R
и проводимость s
, можно по формулам (2.4) и (2.6) найти концентрацию и подвижность носи­ли тока в соответствующем образце.

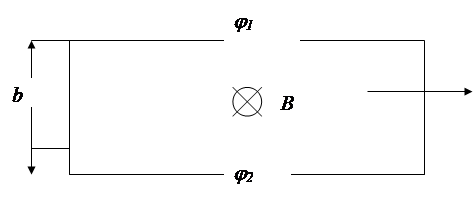
j

– – – – – – – – – – 1
– – – – – – – – – – –

Рис 2.1

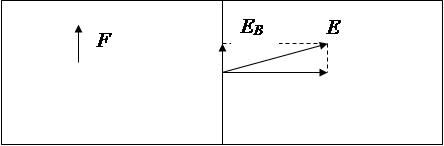
E0

u

+++++++++++++2+++++++++++++

Рис 2.2

3. Эффект Холла в ферромагнетиках.

В ферромагнетиках на электроны про­водимости действует не только внешнее, но и внутреннее магнитное поле:

В = Н + 4pМ

Это приводит к особому ферромагнит­ному эффекту Холла. Экспериментально обнаруже­но, Ex
= (RB + Rа
M)j
, где R
— обык­новенный, a Ra

— необыкновенный (ано­мальный) коэффициент Холла. Между Ra
и удельным электросопротивлением ферромагнетиков установлена корреляция.

4. Эффект Холла в полупроводниках.

Эффект Холла наблюдается не только в металлах, но и в полупроводниках, причем по знаку эффекта можно судить о принадлеж­ности полупроводника к n- или p-типу, так как в полупроводниках n-типа знак носителей тока отрицательный, полупроводниках p-типа – положительный. На рис. 4.1 сопоставлен эффект Холла для образцов с положительными и отрицательными носителями. Направление магнитной силы изменяется на противоположное как при изменении направления движения заряда, так и при изменении его знака. следовательно, при одинаковом направлении тока и поля магнитная сила, действующая на положительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потенциал верхней (на рисунке) грани выше, чем нижней, а в случае отрицательных носителей — ниже. Таким образом, определив знак холловской разности потенциалов, можно установить знак носителей тока. Любопытно, что у некоторых металлов знак Uн
соответствует положительным носителям тока. Объяснение этой аномалии дает квантовая теория.

– – – – – – – – – – –

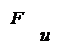
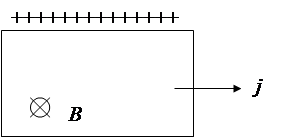
B

– – – – – – – – – – –

+++++++++++++++

Рис 4.1

5. Эффект Холла на инерционных электронах в полупроводниках.

Предсказан новый физический эффект, обусловленный действием силы Лоренца на электроны полупроводника, движущегося ускоренно. Получено выражение для поля Холла и выполнены оценки холловского напряжения для реальной двумерной гетероструктуры. Выполнен анализ возможной схемы усиления холловского поля на примере двух холловских элементов, один из которых — генератор напряжения, а второй — нагрузка.

Известен опыт Толмена и Стюарта, в котором наблюдался импульс тока j
, связанный с инерцией свободных электронов. При инерционном разделении зарядов в проводнике возникает электрическое поле напряженностью E
. Если такой проводник поместить в магнитное поле B
, то следует ожидать появления эдс, аналогичной эффекту Холла, обусловленной действием силы Лоренца на инерционные электроны.

В проводнике, движущемся с ускорением dvx

/dt
, возникает ток jx

и поле Ex

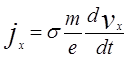, (1)

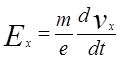, (2)

где s = en
m
— проводимость, m
— подвижность. В магнитном поле B
(0; 0; Bz

) возбуждается поле Ey

= (1/ne
) jx
Bz

или

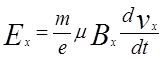(3)

Последнее выражение эквивалентно Ey

= Ex

m
Bz

.

Наиболее подходящий объект для экспериментального наблюдения эффекта — двумерные электроны в гетеросистеме n
-Alx

Ga1-x
As/GaAs. В единичном образце (1×1 см2
) в поле 1 Тл и m@ 104
см2
(В * с) для dvx
/dt
@
10 м/с2
следует ожидать сигнал Vy

@
6*10-11
B, что вполне доступно для современной техники измерений.

Рассмотрим одну из возможностей усиления эффекта на примере двух холловских элементов, один из которых (I) является генератором поля Холла, а второй (II) —нагрузкой. Схема соединений холловских элементов I и II показана на рисунке.

Итак, в магнитном поле Bz

(направление которого на рисунке обозначено знаком Å) в первом холловском элементе (I) возбуждается ток j
(1)
x

, поле E
(1)
x

и холловское поле E
(1)
y

, даваемые выражениями (1)–(3). Замкнув потенциальные (холловские) контакты X
1
—X1

на токовые контакты T
2
—T2

холловского элемента II, в последнем дополнительно к первичному полю E
(2)
x

= E
(1)
x

, определяемому выражением (2), имеем и поле E
(1)
y

. Так что результирующее поле имеет два компонента — E
(2)
x

= E
(1)
x
+ E
(1)
y

. Это возможно, если холловский элемент I рассматривать как генератор напряжения, нагруженный на холловский элемент II. В этом случае должен выполняться режим ”холостого хода”, для чего необходимо выполнить условие R
(X
1
—X
1
)<<R
(T
2
—T
2
), где R
— сопротивление между соответствующими контактами. В таком случае в холловском элементе II возбуждается поле

E(2)
y
=(E(1)
y
+ E(1)
y
)mBz
(4)

учитывая соотношение E
(1)
y
=E
(1)
x

m
Bz
,
получаем

E(2)
y
=(1+mBz
)mBz
E(1)
x
(5)

непосредственное наблюдение эффекта, видимо, затруднено. Более реально осуществить опыты с вибрацией образца в магнитном поле. полезный сигнал ey

при этом может быть отделен от наводки e*
y

по квадратичной зависимости от частоты колебаний w (наводка пропорциональна 1-й степени частоты колебаний).

В самом деле, для данной геометрии опыта (см рисунок) в магнитном поле B
(0; 0; Bz

) при изменении координаты x
со временем по закону x
= x
0
cos wt, где w — частота задающего генератора, нагруженного на пьезоэлемент, и x
0
— амплитуда колебаний последнего, имеем из соотношения (3)

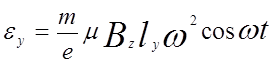(6)

где ly

— расстояние между холловскими контактами образца (X
1
—X
1
) т. е. Ey

= Ey
ly

. Паразитная наводка e*
y

, возникающая в соединительных проводах в соответствии с законом электромагнитной индукции Фарадея, определяется выражением

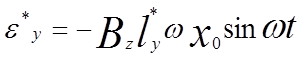(7)

где l*
y

— эффективная длина соединительных проводников, включающих образец в схему измерений. таким образом, полезный сигнал ey

имеет отличительные особенности по отношению к наводке e*
y

. Первая особенность это пропорциональность величине w2
, тогда как e*
y

»w. одновременно ey

во времени изменяется синфазно, а e*
y

— противофазно напряжению задающего генератора. существенно отметить, что масса, входящая в выражения (1)-(3), это масса свободного электрона; величина же подвижности m
определяется эффективной массой.

Рис 5.1

Схема усиления холловского поля из двух элементов I и II.

Указаны направления: знаком
Å
— магнитного поля Bz
; стрелками — ускорения dVx
/dt; полей Холла E(1)
y
, E(2)
y
; плотностей тока j(1)
x
, j(2)
x
.

6. Датчик ЭДС Холла.

Датчик ЭДС Холла – это элемент автоматики, радиоэлектроники и измерительной техники, используемый в качестве измерительного преобразователя, действие которого основано на эффекте Холла. Представляет собой тонкую прямоугольную пластину (площадь – несколько мм2
), или пленку, изготовленную из полупроводника (Si, Ge, InSb, InAs), имеет четыре электрода для подвода тока и съёма ЭДС Холла. Чтобы избежать механических повреждений, пластинки Холла ЭДС датчика монтируют (а пленку напыляют в вакууме) на прочной подложке из диэлектрика (слюды, керамики). Для получения наибольшего эффекта толщина пластины (плёнки) делается возможно меньшей. Датчики ЭДС Холла применяют для бесконтактного измерения магнитных полей (от 10-6
до 105
Э). При измерении слабых магнитных полей пользуются Холла ЭДС датчиками, вмонтированными в зазоре ферро– или ферримагнитного стержня (концентратора), что позволяет значительно повысить чувствительность датчика. Так как в полупроводниках концентрация носителей зарядов (а следовательно, и коэффициент Холла) может зависеть от температуры, то в случае точных измерений необходимо либо термостатировать Холла ЭДС датчик, либо применять сильнолегированные полупроводники (последнее снижает чувствительность датчика).

При помощи Холла ЭДС датчика можно измерять любую физическую величину, которая однозначно связана с магнитным полем; в частности можно изменять силу тока, так как вокруг проводника с током образуется магнитное поле, которое можно измерить. На основе Холла ЭДС датчика созданы амперметры на токи до 100 кА. кроме того Холла ЭДС датчики применяются в измерителях линейных и угловых перемещений, а также в измерителях градиента магнитного поля, магнитного потока и мощности электрических машин, в бесконтактных преобразователях постоянного тока в переменный, и, наконец, в воспроизводящих головках систем звукозаписи.

8. Список используемой литературы.

1) Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика
, т. VIII. Электродинамика сплошных сред
(М., Наука, 1982)

с. 309.

2) И.М. Цидильковский УФН, 115
, 321 (1975).

Редактор Т.А. Полянская

3) Физика и техника полупроводников, 1997, том 31, № 4

4) И.В. Савельев Курс общей физики, т. II. Электричество и магнетизм. Волны. Оптика
: Учебное пособие. – 2-е издание, переработанное (М., Наука, главная редакция физико-математической литературы,1982) с.233 – 235.

5) Большая советская энциклопедия, том 28, третье издание (М., издательство «Советская энциклопедия», 1978) с.338-339.