Загрузка...
Учебная работа. Реферат: Фрактальная размерность стримерных каналов
Балханов Василий Карлович
Бурятский НЦ СО ран, г. Улан-Удэ
Тремя независимыми методами измерена фрактальная размерность плоскостной проекции стримерных каналов. На основе фрактального исчисления скейлинговые показатели полной длины внутри выделенной области и числа ветвлений стримерных каналов выражаются через фрактальную размерность.
Введение. В последнее время активизировалось изучение стримерных разрядов — сети каналов, возникающих при электрическом пробое в диэлектриках (воздухе, полимерных изоляторах, фотоэмульсии) [1,2]. изучение стало особенно актуальным в связи с использование кабелей с полимерной изоляцией [2]. однако отмечается, что количественной теории, описывающей рост ветвления электрического пробоя, до сих пор нет. В статье геометрическую конфигурацию разрядных каналов, рост числа каналов, их ветвление предложено рассматривать как фрактальные разветвленные объекты и описывать их количественно с помощью понятия фрактальной размерности [3-5]. электрический пробой — видимый в оптическом диапазоне стримерный канал в диэлектриках, образованный локально растущим электрическим полем. Пробой возникает, когда на небольшой участок удаленной от заряженной подложки подается такое высокое напряжение, что происходит собственно электрический пробой. Под такое определение подходят разряды молний в воздухе, частичные разряды в эпоксидной смоле, плазменные структуры в фотоэмульсии. В указанном смысле стримерные каналы относятся к классу универсальности, зависящие только от двух безразмерных величин: фрактальной размерности и размерности пространства, в котором происходит процесс. М.Д. Носковым и др. [2] прямым измерением, было определено, что фрактальная размерность D частичных разрядов лежит в пределах 1.45 ¸ 1.55. Н.А. Поповым [1] определялась фрактальная размерность коронного разряда, им получено, что D = 2.16 
0.05. Для разряда молний также измерялась фрактальная размерность, при этом установлено, что на масштабах от десятков метров и выше D = 1. Видим существенное различие в значениях для размерности. В связи с этим в статье тремя независимыми методами измерена фрактальная размерность планового рисунка системы стримерных каналов (рис. 1) [1].
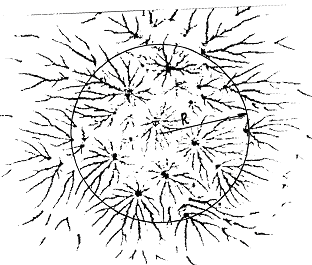
Рис. 1. Система микроразрядов, пересекающих диэлектрическую фотопластинку [1].
используемые методы являются результатами фрактального исчисления [6], основы последнего для связности изложения представлены в следующей части. Изложение в статье теории фрактального исчисления также связано с тем, что начиная с первых книг Б. Мандельброта и кончая научными работами последнего времени, пишут "- структуры, обладающие в том или ином смысле пространственным самоподобием -". Мы дадим замкнутую систему аксиом фрактального исчисления, и теперь не нужно будет говорить "- в том или ином смысле -".
Аксиомы фрактального исчисления. Фрактальная геометрия, открытая Б. Мендельбротом 30 лет назад, основывается на экспериментальном факте, что в общем случае длина L произвольной кривой (которая может быть изломана в любой точке) степенным образом зависит от масштаба измерения d :
L = Cd1-
D
. (1)
здесь С — типичный для фрактальной геометрии размерный множитель, свой для каждой кривой, D — фрактальная размерность. Для обычных, гладких линий D = 1 и получаем "истинную" длину. Если кривая плотно заполняет всю плоскость (простой пример — броуновская траектория), то для нее D = 2. Формулу легко проверить, нарисовав синусоподобную линию и, меняя раствор циркуля, измерить длину такой линии. С появлением формулы Мандельброта (1) сразу же было осознано, что фрактальные линии масштабно — инварианты (самоподобны). Самоподобие означает, что как вся линия, так и любой ее участок обладают одной и той же размерностью. Если линию увеличить в l раз, то для измерения новой длины lL достаточно использовать масштаб, равный ld, т.е.
lL = C(ld ) 1-
D
. (2)
Формулы Мандельброта и условие самоподобия в форме (2) достаточно взять в виде аксиом фрактального исчисления, тогда чисто логическим путем можно получить практически все известные на последнее время результаты. Мы их применим к "разветвленным структурам", к которым относятся и сети стримерных каналов.
Разветвленные структуры. Для построения разветвленных структур возьмем линию и разрежем ее на множество неравнозначных отрезков. Разбросав эти отрезки по плоскости, мы как раз и получаем пример искомых структур. Проведем в (2) замену обозначений, это аналогично тому, что шестиметровую длину сначала измеряем двухметровым масштабом, укладывая ее три раза. Но можно использовать трехметровый масштаб, прикладывая ее только два раза. Итак, переобозначим l на 1/R, где R считаем линейным размером выделяемой области. Тогда из (2) получаем
L = C×d1-
D
×RD
. Убрав все неопределенные масштабные множители, находим:
L ~ R D
. (3)
Применение формулы (3) к определению фрактальной размерности разветвленных структур состоит в следующем. На плановом рисунке стримерных каналов выделяется некоторая область (на рис. 1 это окружность радиусом R), и подсчитывается общая длина всех каналов, попадающих в рассматриваемую область. Так мы получаем первые значения L1
и R1
. Далее выделяется другая область (чуть больше первоначальной), и после подсчета получаются другие значения L2
и R2
. Таким образом, в итоге мы получаем набор значений L и R, по которым методом линейной регрессии строим прямую на осях LnL и LnR. Угловой коэффициент будет равняться фрактальной размерности D. Таким образом было установлено, что для стримерных каналов
D = 1.52 0.03.
Для улучшения статистики нами выбирались разные формы областей разбиения — от прямоугольных до круглых, а также менялось и само число таких разбиений.
Здесь мы изложили первый из используемых методов измерения фрактальной размерности. второй метод измерения состоит в подсчете числа N пересечений ветвлениями стримерных каналов периметра области. На рис. 1 границей выделенной области является окружность радиусом R. Легко сосчитать, что для изображенного на рисунке случая N = 53. Варьируя радиус R, находим, что N и R связаны степенным (скейлинговым) законом:
N~Rn
, (4)
с показателем n = 1.012 0.05. Аппарат фрактального исчисления [6] позволяет связать n с размерностью D, именно:
n = 2 (D -1). (5)
Качественно результат можно обосновать следующим образом. Для обычных дифференцируемых линий число N не должно зависеть от R, т.е. при D = 1 должно быть n = 0. Если линия заполняет всю плоскость, т.е. D = 2, то N будет квадратично зависеть от области, т.е. n = 2. Предполагая линейную зависимость между n и D, приходим к результату (5). При строгом подходе необходимо использовать понятие фрактальной производной, в данном случае от степенной функции (3) с нормирующим множителем 1/R2
:
.
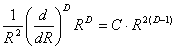
А это и есть формула (4) с показателем (5). теперь находим D = 1 + n / 2 = 1.506 0.005.
Приступим к третьему методу измерения величины D. метод основан на анализе графика на рис. 2 [2], где представлена зависимость роста границы канальных лучей от
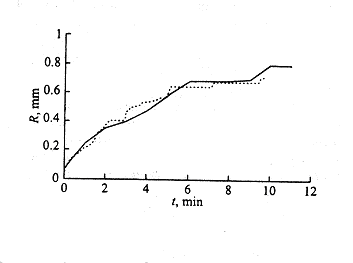
Рис. 2 Зависимость длины дендрита от времени роста. Сплошная кривая — эксперимент, штриховая — моделирование.
времени. Пропорционально со временем увеличивается и число ветвлений, т.е. N~t и из (4) следует, что
R~t1/
n
. (7)
На интервале времен от 1 мин до 6 мин из рис. 2 следует, что R~t0.943
, откуда n = 1.06 и D = 1.53.
Обсуждение. тремя независимыми методами получена фрактальная размерность плоскостной проекции стримерных каналов, представленных на рис. 1. полученные значения 1.53, 1.52 и 1.52 совпадают с данными работы [2]. Согласованность значений для размерности указывает на работоспособность предложенных выше аксиом фрактального исчисления. подобной рис. 2 имеется и результат в работе [1], где полечен следующий закон для числа ветвления: N~R1.18
. Из него следует, что D = 1.59, т.е. близкая к нашим значениям размерность. Из энергетических соображений Н.А. Поповым [1] приведено D = 2.16, отличие этого значения от 1.59 указывает, что величина D = 2.16 относится только к скейлинговому показателю и еще предстоит задача связать ее с фрактальной размерностью.
полученный в работах [1,2] и нами усредненный результат D = 1.53 указывает на выполнение закона класса универсальности для электрических разрядов в различных диэлектрических средах.
Список литературы
Попов Н.А. исследование пространственной структуры ветвящихся стримерных каналов коронного разряда // Физика плазмы, 2002, том 28, ¦ 7, с. 664-672.
Носков М.Д., Малиновский А.С., Закк М., Шваб А.Й. Моделирование роста дендритов и частичных разрядов в эпоксидной смоле // ЖТФ, 2002, том 72, вып. 2, с. 121-128.
Федер Е. Фракталы. — М.: мир, 1991, 254 с.
Шредер М. Фракталы, хаос, степенные законы. — Ижевск: НИЦ "Регулярная и хаотическая динамика", 2001, 528 с.
Божокин С.В., Паршин Д.А. Фракталы и мультифракталы. — Ижевск: НИЦ "регулярная и хаотическая динамика", 2001, 128 с.
Балханов В.К. Введение в теорию фрактального исчисления. — Улан-Удэ.: Изд. Бурятского гос. ун-та, 2001, 58 с.