Учебная работа. Реферат: Исследование динамики финансовых рынков нейросетевыми методами

Учебная работа. Реферат: Исследование динамики финансовых рынков нейросетевыми методами

СОДЕРЖАНИЕ

ВВЕДЕНИЕ
………………………………………..………………………………3

ГЛАВА 1

понятие ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ

1.1. Искусственный нейрон: понятие, индивидуальности структуры……….7

1.2. Искусственные нейронные сети: их характеристики и систематизация..12

1.3. Обучение нейронных сетей………………………………………..19

ГЛАВА 2

ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ

2.1. Индивидуальности внедрения искусственных нейронных сетей в разных областях……………………………………………………….23

2.2. Применение нейронных сетей в биржевой деятель………..28

2.3. Ограничения и недочеты, связанные с внедрением нейронных сетей на бирже……………………………………………….33

ГЛАВА 3

исследование ДИНАМИКИ ФИНАНСОВЫХ РЫНКОВ НЕЙРОСЕТЕВЫМИ МЕТОДАМИ

3.1. задачки и способы нейросетевого анализа и прогнозов……………38

3.2. Нейросетевые прогнозы доходностей…………………………….44

ЗАКЛЮЧЕНИЕ
…………………………………………………………………52

СПИСОК ИСТОЧНИКОВ
…………………………………………………….54

ВВЕДЕНИЕ

Искусственные нейронные сети, подобно биологическим, являются вычислительной системой с большущим числом параллельно функционирующих обычных микропроцессоров с обилием связей. Невзирая на то, что при построении таковых сетей обычно делается ряд допущений и значимых упрощений, отличающих их от био аналогов, искусственные нейронные сети показывают необычное число параметров, присущих мозгу, – это обучение на базе опыта, обобщение, извлечение существенных данных из лишней инфы.

Нейронные сети могут поменять свое сеть быть может устойчивой к неким отклонениям входных данных, что дозволяет ей верно «созидать» образ, содержащий разные помехи и преломления. сейчас существует огромное число разных конфигураций нейронных сетей с разными принципами функционирования, которые нацелены на решение самых различных задач. Они интенсивно используются там, где обыденные алгоритмические решения оказываются неэффективными либо совсем неосуществимыми. Практика использования нейросетей показала их эффективность в таковых областях, как прогнозирование, выявление зависимостей, ситуационное управление. Все это применимо на денежных рынках. Этот инструментарий дозволяет выявлять и получать новейшие познания о динамике цены ценных бумаг, о конфигурациях характеристик экономической активности и о колебаниях обменного курса валют, включая, муниципальные облигации. На базе этих познаний можно выявить взаимозависимости, имеющиеся меж этими чертами, что в свою очередь дозволяет значимым образом повысить надежность прогнозирования.

В истинное время применение нейронных сетей к задачкам биржевой деятель в особенности животрепещуще, так как классические, ставшие уже традиционными, подходы были разработаны для описания относительно устойчивого, медлительно эволюционирующего и не конструктивно изменяющегося мира, мира – который еще не очень отклонился от состояния равновесия. По самой собственной сущности эти способы и подходы не были предусмотрены для описания и моделирования стремительных конфигураций, непредсказуемых скачков и сложных взаимодействий отдельных составляющих современного мирового рыночного процесса.

Как понятно, украинский Рынок ценных бумаг за свою новейшую постсоветскую историю пережил много добротных и нехороших времен. Денежный кризис 1998 года практически разрушил этот сектор экономики. Но следует осознавать, что без развитого рынка ценных бумаг выстроить рыночную экономику нереально. Одним из важных направлений развития Украины обязано стать принципное изменение роли рынка ценных бумаг в денежной системе страны и его хозяйственном механизме в целом. Большие усилия страны должны быть ориентированы на увеличение доверия инвесторов к украинской экономике. одной из принципиальных задач на пути стабилизации фондового рынка Украины является вербование личных лиц для инвестирования в компании и большие компании нашей страны. Для инвесторов особо нужным и животрепещущим является возможность прогнозирования ситуации на рынке ценных бумаг. Прогнозирование подразумевает научно-обоснованное суждение о вероятных состояниях экономической системы в дальнейшем, о других путях и сроках его воплощения, оно обязано полагать получение высококачественных оценок этих состояний с помощью математических и инструментальных средств реализации.

вместе с большими государственными фондовыми, фьючерсными, денежными биржевыми рынками, возникли рынки мирового масштаба. Обычный пример – современный денежный Рынок FOREX, сейчас представляет собой всемирную сеть банков, вкладывательных фондов и брокерских домов, которая содержит в себе связанную компьютерную инфраструктуру, обслуживающую клиентов, торгующих валютами, заключающих спекулятивные сделки для того, чтоб получить Прибыль от раз в секунду изменяющихся курсов валют. Уже на данный момент каждодневный оборот на рынке FOREX превосходит один триллион баксов (что осязаемо даже в масштабах страны), а согласно прогнозам профессионалов он будет возрастать и далее. Понятно, что приблизительно 99% всех сделок на денежных рынках – спекулятивные, т.е. заключаемые только с целью извлечения прибыли по схеме «приобрести дешевле – реализовать дороже». Они все основаны на пророчествах конфигураций котировок участниками рынка. Для действенного анализа рынка требуются надлежащие современным требованиям экономико-математические способы. сейчас большущее количество «западных» ученых работают в области разработки способов прогнозирования денежных рынков. Таковым образом, исследования в области биржевых рынков – животрепещущее и перспективное направление деятель и будет оставаться таким в течение долгого периода времени.

Целью нашей работы является подробное исследование внедрения нейронных сетей к задачкам биржевой деятель, подтверждение их эффективности в управлении капиталом и анализе денежных рынков.

Для заслуги поставленной цели нужно решить последующие задачки: ознакомится со структурой нейронных сетей, правилами и принципами их функционирования; возможностью их внедрения при решении заморочек пророчества, систематизации, моделирования денежных временных рядов, также оптимизации в области денежного анализа и управления риском.

Объектом исследования является внедрение систем, базирующихся на искусственных нейронных сетях, интенсивно применяемых для прогнозирования денежных рынков.

Предметом ­­– нейронная сеть, прогнозирующая дневную динамику таковых денежных инструментов: курс бакс США

В первой главе описано понятие нейрона, нейронной сети. Тщательно описаны принципы работы искусственных нейронных сетей, дана их систематизация.

2-ая глава даёт детализированное возможности создать систему самообучающейся, что в особенности принципиально для трудноформализуемых задач. Благодаря способности работы с «зашумленными» данными (нечеткие нейроны) система выходит гибкой и, хотя обычно не решает задачку со 100%-ной точностью, может принести значительную Прибыль в денежной сфере.

3-я глава показывает способность умственных систем на базе искусственных нейронных сетей с фуррором решать задачки прогнозирования. При всем этом показано, что более прогнозируемо направление хода цены. Наиболее сложной задачей является прогнозирование длины хода.

Таковым образом, при анализе и пророчестве сложных денежных систем в истинное время недозволено обойтись без такового массивного инструмента как нейросетевые технологии. Нейронные сети находят все новейшие удачные внедрения в практике управления и принятия решений, в том числе – в денежной и торговой сферах. Лежащая в их базе теория нелинейных адаптивных систем обосновала свою полезность при выработке прогнозов в целом ряде отраслей экономики и денег.

ГЛАВА 1. ПОНЯТИЕ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ

1.1.
Искусственный нейрон: понятие, индивидуальности структуры

Под нейронными сетями предполагаются вычислительные структуры, которые моделируют обыкновенные био процессы, обычно ассоциируемые с действиями людского мозга . Они представляют собой распределенные и параллельные системы, способные к адаптивному обучению методом анализа положительных и отрицательных действий. Простым преобразователем в данных сетях является искусственный нейрон либо просто ней­рон, нареченный так по аналогии с биологическим макетом.

К истинному времени предложено и исследовано огромное ко­личество моделей нейроподобных частей и нейронных сетей.

Искусственный нейрон является основой хоть какой искусственной нейронной сети. Нейроны представляют собой относительно обыкновенные, однотипные элементы, имитирующие работу нейронов мозга . Любой нейрон характеризуется своим текущим состоянием по аналогии с нервными клеточками мозга, которые могут быть возбуждены и заторможены.

Искусственный нейрон, также как и его естественный макет, имеет группу синапсов (входов), которые соединены с выходами остальных нейронов, также аксон – выходную связь данного нейрона – откуда сигнал возбуждения либо торможения поступает на синапсы остальных нейронов.

Вид нейрона представлен на рисунке 1.1., где
– сигнал, поступающий от нейрона
– скалярное произведение вектора входных сигналов и вектора весов;
функция возбуждения;
выходной сигнал нейрона.

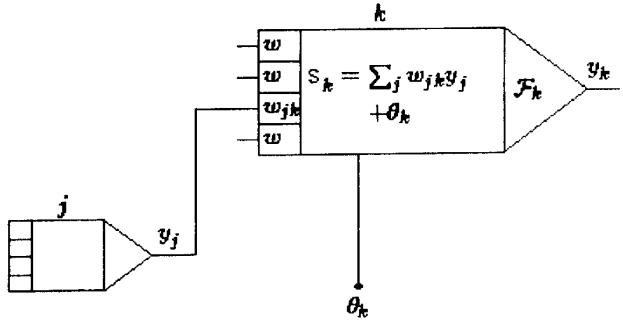
Рис. 1.2. Искусственный нейрон – простой элемент искусственной нейронной сети

Источник: [7, с. 22]

Таковым образом, нейрон состоит из частей 3-х ти­пов: умножителей (синапсов), сумматора и нелинейного преобра­зователя. Синапсы производят связь меж нейронами, умно­жают входной сигнал на число, характеризующее силу связи (вес синапса). Сумматор делает сложение сигналов, поступающих по синаптическим связям от остальных нейронов, и наружных входных сигналов. Нелинейный преобразователь реализует нелинейную функцию 1-го аргумента — выхода сумматора. Эта функция на­зывается функцией активации либо передаточной функциейнейрона. Нейрон в целом реализует скалярную функцию векторного аргумента. Математическая модель нейрона:

S=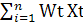 + b (1.1)

Y= f(s) (1.2)

где Wt
– вес синапса, i= 1…n; b–

В общем случае входной сигнал, весовые коэффициенты и смещение могут принимать действительные значения, а в почти всех практических задачках – только некие фиксированные значения. Выход (у) определяется видом функции активации и быть может как реальным, так и целым.

Синаптические связи с положительными весами именуют возбуждающими, с отрицательными весами – тормозящими.

Описанный вычислительный элемент можно считать упро­щенной математической моделью био нейронов. Чтоб выделить различие нейронов био и искусственных, 2-ые время от времени именуют нейроноподобными элементами либо формальными нейронами.

На входной сигнал (s) нелинейный преобразователь отвеча­ет выходным сигналом f(s), который представляет собой выход у нейрона. Главные разновидности активационных функций, используемых в

нейронных сетях, представлены на рис. 1.2.

Рис. 1.2. Активационная функция

а) пороговая; b) полулинейная; c) сигмоидальная

Источник: [2, с. 45]

В качестве активационной функции нередко употребляется сигмоидальная (s-образная либо логистическая) функция, показанная на рис. 1.2 с. Эта функция математически выражается по формуле

f(x) = 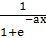(1.3)

При уменьшении α сигмоидальная функция становится наиболее пологой, в пределе при α=0 вырождаясь в горизонтальную линию на уровне 0,5; при

увеличении α сигмоидальная функция приближается по наружному виду к функции единичного скачка с порогом T в точке x=0. Из выражения для сигмоидальной функции видно, что выходное

f (x) = α f (x) (1- f (x)) (1.3)

Необходимо подчеркнуть, что сигмоидальная функция дифференцируема на всей оси абсцисс, что употребляется в неких методах обучения. Не считая того, сигмоидальная функция владеет свойством усиливать малые сигналы лучше, чем огромные, тем предотвращая насыщение от огромных сигналов, потому что они соответствуют областям аргументов, где сигмоидальная функция имеет пологий наклон.

Выбор структуры нейронной сети осуществляется в согласовании с чертами и сложностью задачки. Для решения неких отдельных типов задач уже есть рациональные, на нынешний денек конфигурации, описанные, к примеру, в [6, 7, 8]. Если же задачка не быть может сведена ни к одному из узнаваемых типов, разрабу приходится решать сложную делему синтеза новейшей конфигурации.

На теоретическом уровне число слоев и число нейронов в любом слое нейронной сети быть может произвольным, но практически оно ограничено ресурсами компа либо спец микросхемы, на которых обычно реализуется нейронная сеть. При всем этом, если в качестве активационной функции для всех нейронов сети употребляется функция единичного скачка, нейронная сеть именуется мультислойным персептроном.

В нейронных сетях, именуемых персептронами, употребляется активационная функция единичного скачка.

Также примерами активационных функций являются: полулинейная, линейная, логистическая (сигмоидальная), гиперболический тангенс, экспоненциальная, синусоидальная, сигмоидальная (рациональная), шаговая (линейная с насы­щением), пороговая, модульная, знаковая (сигнатурная), квадратичная.

1.2. Искусственные нейронные сети:
их характеристики и
к
лассификация

Нейронная сеть представляет собой совокупа нейроподобных частей, определенным образом соединенных друг с другом и с наружной средой при помощи связей, определяемых ве­совыми коэффициентами.

Зависимо от функций, выполняе­мых нейронами в сети, можно выделить три их типа:

• входные нейроны, на которые подается вектор, кодирую­щий входное действие либо образ наружной среды; в их обычно не осуществляется вычислительных процедур, а информация пе­редается с входа на выход методом конфигурации их активации;

• выходные нейроны, выходные значения которых пред­ставляют выходы нейронной сети; преобразования в их осущест­вляются по выражениям (1.1) и (1.2);

• промежные нейроны, составляющие базу нейрон­ных сетей, преобразования в каких производятся также по вы­ражениям (1.1) и (1.2).

В большинстве нейронных моделей тип нейрона связан с его расположением в сети. Если нейрон имеет лишь выходные связи, то это входной нейрон, если напротив – выходной нейрон. Но вероятен вариант, когда выход топологически внутреннего нейрона рассматривается как часть выхода сети. В процессе функциониро­вания сети осуществляется преобразование входного вектора в выходной, некая переработка инфы. Определенный вид выполняемого сетью преобразования данных обусловливается не только лишь чертами нейроподобных частей, да и особен­ностями ее архитектуры, а конкретно топологией межнейронных связей, выбором определенных подмножеств нейроподобных элемен­тов для ввода и вывода инфы, методами обучения сети, наличием либо отсутствием конкуренции меж нейронами, на­правлением и методами управления и синхронизации передачи инфы меж нейронами.

Исходя из убеждений топологии можно выделить три главных ти­па нейронных сетей:

• полносвязные (рис. 1.4. а);

• мультислойные либо слоистые (рис. 1.4. б);

• слабосвязные (с локальными связями) (рис. 1.4. в).

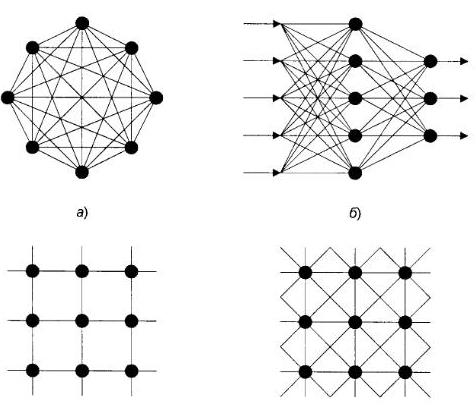
Рис. 1.3. Архитектуры нейронных сетей

Источник: [12, с. 35]

В полносвязных нейронных сетях любой нейрон передает собственный выходной сигнал остальным нейронам, в том числе и себе. Все входные сигналы подаются всем нейронам. Выходными сигналами сети могут быть все либо некие выходные сигналы нейронов опосля нескольких тактов функционирования сети.

В мультислойных нейронных сетях нейроны соединяются воединыжды в слои. Слой содержит совокупа нейронов с едиными входными сигналами. Число нейронов в слое быть может хоть каким и не зави­сит от количества нейронов в остальных слоях. В общем случае сеть состоит из Q слоев, пронумерованных слева вправо. Наружные входные сигналы подаются на входы нейронов входного слоя (его нередко нумеруют как нулевой), а выходами сети являются выходные сигналы крайнего слоя. Не считая входного и выходного слоев в мультислойной нейронной сети есть один либо несколько укрытых слоев. Связи от выходов нейронов некого слоя q к входам нейронов последующего слоя (q+1) именуются поочередными.

Входной слой Сокрытый слой Выходной слой

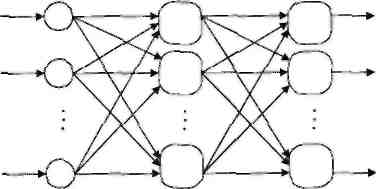
Рис 1.4. Мультислойная (двухслойная) сеть прямого распространения

Источник: [15, с. 55]

В свою очередь, посреди мультислойных нейронных сетей вы­деляют последующие типы.

1) Однообразные. Это личный вариант слоистых сетей с доп ус­ловиями на связи и нейроны. Любой слой не считая крайнего (вы­ходного) разбит на два блока: возбуждающий и тормозящий. Связи меж блоками тоже делятся на тормозящие и возбуждаю­щие. Если от нейронов блока А к нейронам блока В ведут лишь возбуждающие связи, то это значит, что хоть какой выходной сигнал блока является однотонной неубывающей функцией хоть какого вы­ходного сигнала блока А. Если же эти связи лишь тормозящие, то хоть какой выходной сигнал блока В является невозрастающей функ­цией хоть какого выходного сигнала блока А. Для нейронов монотон­ных сетей нужна однообразная зависимость выходного сигна­ла нейрона от характеристик входных сигналов

2) Сети без оборотных связей. В таковых сетях нейроны вход­ного слоя получают входные сигналы, конвертируют их и передают
нейронам первого укрытого слоя, и так дальше прямо до выходного,
который выдает сигналы для интерпретатора и юзера. Ес­ли не обсуждено неприятное, то любой выходной сигнал q-го слоя
подастся на вход всех нейронов (q+1)-го слоя; но вероятен
вариант соединения q-го слоя с произвольным (q+р)-м слоем.

Посреди мультислойных сетей без оборотных связей различают полносвязанные (выход всякого нейрона q-го слоя связан с вхо­дом всякого нейрона ((q+1)-го слоя) и отчасти полносвязанные. Традиционным вариантом слоистых сетей являются полносвязан­ные сети прямого распространения (рис. 1.4).

3) Сети с оборотными связями. В сетях с оборотными связя­ми информация с следующих слоев передается на прошлые.
Посреди их, в свою очередь, выделяют последующие.

· Слоисто-циклические, отличающиеся тем, что слои замк­нуты в кольцо, крайний слой передает свои выходные сигналы первому; все слои равноправны и могут как получать входные сиг­налы, так и выдавать выходные;

· Слоисто-полносвязанные состоят из слоев, любой из ко­торых представляет собой полносвязную сеть, а сигналы переда­ются как от слоя к слою, так и снутри слоя; в любом слое цикл ра­боты распадается на три части: прием сигналов с предшествующего слоя, обмен сигналами снутри слоя, выработка выходного сигнала и передача к следующему слою.

· Полносвязанно-слоистые по собственной структуре аналогич­ные слоисто-полносвязанным, но функционирующим по-другому: в их не делятся фазы обмена снутри слоя и передачи сле­дующему, на любом такте нейроны всех слоев принимают сигна­лы от нейронов как собственного слоя, так и следующих.

В слабосвязных нейронных сетях нейроны размещаются в узлах прямоугольной либо гексагональной сетки. Любой нейрон связан с 4-мя (округа фон Неймана), шестью (окрест­ность Голея) либо восемью (округа Мура) своими наиблежайшими соседями.

Известные нейронные сети можно поделить по типам струк­тур нейронов на гомогенные (однородные) и гетерогенные. Гомо­генные сети состоят из нейронов 1-го типа с единой функцией активации, а в гетерогенную сеть входят нейроны с разными функциями активации.

Есть бинарные и аналоговые сети. 1-ые из их оперируют лишь двоичными сигналами, и выход всякого нейрона может принимать состояние).

Еще одна систематизация разделяет нейронные сети на синхрон­ные и асинхронные. В первом случае в любой момент времени только один нейрон меняет свое состояние, во 2-м – состояние изменяется сходу у целой группы нейронов, как правило, у всего слоя. Алгоритмически ход времени в нейронных сетях задается итерационным выполнением однотипных действий над нейронами.

Сети можно систематизировать также по числу слоев. Теоре­тически число слоев и число нейронов в любом слое быть может произвольным, но практически оно ограничено ресурсами ком­пьютера либо специализированных микросхем, на которых обычно реализуется нейронная сеть. Чем труднее сеть, тем наиболее слож­ные задачки она может решать.

Выбор структуры нейронной сети осуществляется в соответ­ствии с чертами и сложностью задачки. Для решения от­дельных типов задач уже есть рациональные конфигурации, описанные в приложении. Если же задачка не быть может сведена ни к одному из узнаваемых типов, приходится решать сложную про­блему синтеза новейшей конфигурации При всем этом нужно руково­дствоваться последующими главными правилами.

· способности сети растут с повышением числа ней­ронов сети, плотности связей меж ними и числом слоев.

· Введение оборотных связей вместе с повышением воз­можностей сети поднимает вопросец о динамической стойкости сети.

· Сложность алгоритмов функционирования сети, введение нескольких типов синапсов содействует усилению мощности ней­ронной сети.

вопросец о нужных и достаточных свойствах сети для решения задач того либо другого рода представляет собой целое на­правление нейрокомпьютерной науки. Потому что неувязка синтеза нейронной сети очень зависит от решаемой задачки, отдать общие подробные советы проблемно. Почти всегда лучший вариант выходит на базе интуитивного подбо­ра, хотя в литературе приведены подтверждения того, что для лю­бого метода существует нейронная сеть, которая может его воплотить.

Почти все задачки определения образов (зрительных, рече­вых), выполнения многофункциональных преобразований при обработке сигналов, управления, прогнозирования, идентификации сложных систем, сводятся к последующей математической постановке. Необ­ходимо выстроить такое отображение X→ У, чтоб на любой вероятный входной сигнал X формировался верный выход­ной сигнал У. Отображение задается конечным набором пар (<вход>, <узнаваемый выход>). Число этих пар (обучающих приме­ров) значительно меньше общего числа вероятных сочетаний значений входных и выходных сигналов. совокупа всех обучающих примеров носит заглавие обучающей подборки.

В задачках определения образов X- некое представ­ление вида (изображение, вектор),
номер класса, к которому принадлежит входной образ. В задачках управления X- набор контролируемых парамет­ров управляемого объекта, У — код, определяющий управляющее действие, соответственное текущим значениям контролируе­мых характеристик. В задачках прогнозирования в качестве входных сигналов ис­пользуются временные ряды, представляющие значения контро­лируемых переменных на неком интервале времени. Выход­ной сигнал – огромное количество переменных, которое является подмноже­ством переменных входного сигнала. При идентификации X и У представляют входные и выход­ные сигналы системы соответственно.

Совершенно говоря, большая часть прикладных задач быть может сведена к реализации некого сложного многофункционального многомерного преобразования.

В итоге отображения X→
нужно обеспечить формирование правильных выходных сигналов в согласовании:

– со всеми примерами обучающей подборки;

– со всеми вероятными входными сигналами, которые не вошли в обучающую подборку. 2-ое требование в значимой степени усложняет задачку формирования обучающей подборки. В общем виде эта задачка в истинное время ещё не решена, но во всех узнаваемых вариантах быть может найдено личное решение.

1.3.
Обучение нейронных сетей

Способность к обучению является главным свойством мозга . Для искусственных нейронных сетей под обучением понимается процесс опции архитектуры сети (структуры связей меж нейронами) и весов синаптических связей (влияющих на сигналы коэффициентов) для действенного решения поставленной задачки. Обычно обучение нейронной сети осуществляется на некой выборке [3]. По мере процесса обучения, который происходит по некому методу, сеть обязана все лучше и вернее реагировать на входные сигналы.

Разумеется, что функционирование нейронной сети, т. е. деяния, которые она способна делать, зависит от величин синоптических связей. Потому, задавшись структурой нейронной сети, отвечающей определенной задачке, разраб должен отыскать рациональные значения для всех весовых коэффициентов w. От того, как отменно будет выполнено обучение , зависит способность сети решать во время эксплуатации поставленные перед ней препядствия. Важными параметрами обучения являются: свойство подбора весовых коэффициентов и время, которое нужно затратить на обучение . Как правило, два этих параметра соединены меж собой оборотной зависимостью и их приходится выбирать на базе компромисса.

Выделяют три парадигмы обучения: с учителем, самообучение и смешанная.

При обучении с учителем нейронной сети предъявляются значения как входных, так и выходных характеристик, и она по некому внутреннему методу подстраивает веса собственных синаптических связей.

Обучение с учителем подразумевает, что для всякого входного вектора существует мотивированной вектор, представляющий из себя требуемый выход. совместно они именуются представительской либо обучающей подборкой. Обычно нейронная сеть учится на неком числе таковых выборок. Предъявляется выходной вектор, рассчитывается выход нейронной сети и сравнивается с подходящим мотивированным вектором, разность (ошибка) при помощи оборотной связи подается в нейронную сеть, и веса меняются в согласовании с методом, стремящимся минимизировать ошибку. Векторы обучающего огромного количества предъявляются поочередно, рассчитываются ошибки и веса подстраиваются для всякого вектора до того времени, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.

При обучении без учителя нейронной сети предъявляются лишь входные сигналы, а выходы сети формируются без помощи других с учетом лишь входных и производных от их сигналов. Невзирая на бессчетные прикладные заслуги, обучение с учителем критиковалось за свою биологическую неправдоподобность. Тяжело вообразить обучающий механизм в естественном людском уме, который бы ассоциировал желаемые и действительные значения выходов, выполняя корректировку при помощи оборотной связи. Если допустить схожий механизм в людском системы животных, обычно расположенный в головном отделе тела и представляющий собой компактное скопление нервных клеток и их отростков) — центральный отдел нервной системы человека и звериных, то откуда тогда появляются желаемые выходы? Обучение без учителя является наиболее правдоподобной моделью обучения в био системе. Развитая Кохоненом и почти всеми иными, она не нуждается в мотивированном векторе для выходов и, как следует, не просит сопоставления с предопределенными безупречными ответами. Обучающее огромное количество состоит только из входных векторов. Обучающий метод подстраивает веса нейронной сети так, чтоб выходили согласованные выходные векторы, т. е. чтоб предъявление довольно близких входных векторов давало однообразные выходы. процесс обучения, как следует, выделяет статистические характеристики обучающего огромного количества и группирует схожие векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения нереально предсказать, какой выход будет выполняться данным классом входных векторов. Как следует, выходы схожей сети должны трансформироваться в некую понятную форму, обусловленную действием обучения. Это не является суровой неувязкой. Обычно легко идентифицировать связь меж входом и выходом, установленную сетью.

Существует огромное число алгоритмов обучения, нацеленных на решение различных задач [4]. Посреди их выделяет метод оборотного распространения ошибки, который является одним из более удачных современных алгоритмов. Его основная мысль состоит в том, что изменение весов синапсов происходит с учетом локального градиента функции ошибки. Разница меж настоящими и правильными ответами нейронной сети, определяемыми на выходном слое, распространяется в оборотном направлении – навстречу сгустку сигналов. В итоге любой нейрон способен найти вклад всякого собственного веса в суммарную ошибку сети. Простейшее правило обучения соответствует способу наискорейшего спуска, другими словами конфигурации синаптических весов пропорционально их вкладу в общую ошибку. естественно, при таком обучении нейронной сети нет убежденности, что она обучилась лучшим образом, так как постоянно существует возможность попадания метода в локальный минимум. Для этого употребляются особые приемы, дозволяющие «вышибить» отысканное решение из локального экстремума. Если опосля нескольких таковых действий нейронная сеть сходится к тому же решению, то можно прийти к выводу о том, что отысканное решение, быстрее всего, нормально.

Итак, нейронная сеть представляет собой совокупа нейроподобных частей, определенным образом соединенных друг с другом и с наружной средой при помощи связей, определяемых ве­совыми коэффициентами.

Известные нейронные сети можно поделить по типам струк­тур нейронов на гомогенные (однородные) и гетерогенные. Гомо­генные сети состоят из нейронов 1-го типа с единой функцией активации, а в гетерогенную сеть входят нейроны с разными функциями активации.

Есть бинарные и аналоговые сети. 1-ые из их оперируют лишь двоичными сигналами, и выход всякого нейрона может принимать состояние).

Еще одна систематизация разделяет нейронные сети на синхрон­ные и асинхронные.

Выделяют три парадигмы обучения: с учителем, самообучение и смешанная.

Возможными областями внедрения искусственных нейронных сетей являются те, где человечий ум малоэффективен, а классические вычисления трудоемки либо на физическом уровне неадекватны (т.е. не отражают либо плохо отражают настоящие физические процессы и объекты). Вправду, актуальность внедрения нейронных сетей неоднократно увеличивается тогда, когда возникает необходимость решения плохо формализованных задач.

Таковым, образом, искусственные нейронные сети, подобно биологическим, являются вычислительной системой с большущим числом параллельно функционирующих обычных микропроцессоров с обилием связей.

ГЛАВА 2. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ

2.1. Индивидуальности внедрения искусственных нейронных сетей в разных областях

Возможными областями внедрения искусственных нейронных сетей являются те, где человечий ум малоэффективен, а классические вычисления трудоемки либо на физическом уровне неадекватны (т.е. не отражают либо плохо отражают настоящие физические процессы и объекты). Вправду, актуальность внедрения нейронных сетей неоднократно увеличивается тогда, когда возникает необходимость решения плохо формализованных задач.

Типовые задачки, решаемые при помощи нейронных сетей и нейрокомпьютеров последующие:

— автоматизация процесса систематизации;

— автоматизация прогнозирования;

— автоматизация процесса пророчества;

— автоматизация процесса принятия решений;

— управление;

— кодирование и декодирование инфы;

— аппроксимация зависимостей и др.

Разглядим индивидуальности внедрения нейронных сетей, которые демонстрируют их достоинства посравнению с иными существующими способами при выбирании модели прогноза.

1. Результативность при решении неформализованных либо плохо формализованных задач. Из общеизвестных преимуществ способов на базе нейронных сетей следует выделить одно самое симпатичное – отсутствие необходимости в серьезной математической спецификации модели, что в особенности ценно при прогнозировании плохо формализуемых действий. Понятно, что большая часть денежных, бизнес и остальных схожих задач плохо формализуется.

2. Устойчивость к частым изменениям среды. Плюсы нейронных сетей стают видными, когда нередко меняются «правила игры»: среда, в какой существует предсказуемый процесс, также нрав действия влияющих причин. Потому, нейронные сети лучшим образом подступают для решений таковых задач, как прогнозирование тенденций фондового рынка, характеризующихся воздействием целого набора повсевременно изменяющихся причин.

3. Результативность при работе с огромным объемом противоречивой инфы. Нейронные сети будут лучше там, где имеется весьма много анализируемых данных, в каких укрыты закономерности. В этом случае автоматом учитываются также разные нелинейные взаимодействия меж влияющими факторами. Это в особенности принципиально, а именно, для подготовительного анализа либо отбора начальных данных, выявления «выпадающих фактов» либо грубых ошибок при принятии решений.

4. Результативность при работе с неполной информацией. Целенаправлено внедрение нейронных сетей в задачках с неполной либо «зашумленной» информацией, также в задачках, для которых свойственны интуитивные решения.

Уже сейчас искусственные нейронные сети употребляются в почти всех областях. В крайнее время предпринимаются активные пробы объединения искусственных нейронных сетей и экспертных систем. В таковой системе искусственная нейронная сеть может реагировать на большая часть относительно обычных случаев, а все другие передаются для рассмотрения экспертной системе. В итоге сложные случаи принимаются на наиболее высочайшем уровне, при всем этом, может быть, со сбором доп данных либо даже с привлечением профессионалов.

области внедрения нейронных сетей очень многообразны – это определение текста и речи, семантический поиск, экспертные системы и системы поддержки принятия решений, пророчество курсов акций, системы сохранности, анализ текстов. Одной из более сложных и нужных возможностей нейронных сетей является прогнозирование. Ведь оно является важным элементом современных информационных технологий принятия решений в управлении. Эффективность того либо другого управленческого решения оценивается по событиям, возникающим уже опосля его принятия. Потому прогноз неуправляемых качеств таковых событий перед принятием решения дозволяет создать лучший выбор, который, без прогнозирования мог бы быть не таковым удачным.

задачи прогнозирования соединены с недостающим качеством и количеством начальных данных, переменами среды, в какой протекает процесс, действием личных причин. Прогноз постоянно осуществляется с некой погрешностью, которая зависит от применяемой модели прогноза и полноты начальных данных. При увеличении информационных ресурсов, применяемых в модели, возрастает точность прогноза, а убытки, связанные с неопределенностью при принятии решений, уменьшаются. нрав издержек, связанных с прогнозированием, такой, что за определенным пределом доп Издержки не приведут к понижению утрат. Это соединено с тем, что беспристрастно нереально понизить погрешность прогнозирования ниже определенного уровня, вне зависимости от того как неплох примененный способ прогнозирования. Потому определение погрешности прогноза, вместе с самим прогнозом, дозволяет существенно понизить риск при принятии решений.

Разглядим несколько в особенности ярчайших и увлекательных примеров использования нейронных сетей в различных областях.

1. техника и телекоммуникации. Одна из важных задач в области телекоммуникаций, которая заключается в нахождении рационального пути пересылки трафика меж узлами, быть может удачно решена при помощи нейронных сетей. В данном случае нужно принимать во внимание то, что, во-1-х, предложенное решение обязано учесть текущее состояние сети, свойство связи и наличие сбойных участков, а во-2-х, поиск рационального решения должен осуществляться в настоящем времени. Нейронные сети отлично подступают для решения задач такового рода. Не считая управления маршрутизацией потоков, нейронные сети могут употребляться и при проектировании новейших телекоммуникационных сетей, позволяя получать очень действенные решения.

2. Информационные технологии.Определение темы текстовых сообщений может служить примером удачного использования искусственных нейронных сетей.

3. Экономика и деньги.Нейронные сети интенсивно используются на денежных рынках. Это нейросетевые пророчества, нейросетевые системы для подготовительной обработки транзакций на денежных биржах ряда государств, отслеживание подозрительных сделок.

4. реклама и маркетинг. При ведении бизнеса в критериях конкуренции компаниям нужно поддерживать неизменный контакт с пользователями, обеспечивая оборотную связь. Для этого некие компании проводят опросы потребителей, дозволяющие узнать, какие причины являются решающими при покупке данного продукта либо услуги. Анализ результатов подобного опроса— сложная задачка, так как нужно изучить огромное количество связанных меж собой характеристик и выявить причины, оказывающие наибольшее воздействие на Спрос. Имеющиеся нейросетевые способы разрешают узнать это и предсказывать означает, отыскивать рациональные стратегии работы компании.

5. Здравоохранение. В мед диагностике нейронные сети часто употребляются совместно с экспертными системами.

Приведенные примеры демонстрируют, что технологии нейронных сетей применимы фактически в хоть какой области. Повсеместное проникновение нейронных технологий в остальные области— лишь вопросец времени. Естественно, внедрение новейших наукоемких технологий— процесс непростой, но практика указывает, что Инвестиции не только лишь окупаются и приносят выгоду, да и дают тем, кто их употребляет, осязаемые достоинства.

2.2. Применение нейронных сетей в биржевой деятель

Подавляющее большая часть задач прогнозирования на базе нейронных сетей так либо по другому соединены со сферой бизнеса и денег. Это – короткосрочные и длительные прогнозы тенденций последующих денежных рынков:

· рынков купонных и бескупонных облигаций,

· фондовых рынков (рынков акций),

· денежных рынков.

Сюда же можно отнести прогнозы:

· платежеспособного спроса;

· продаж и выручки;

· рисков кредитования;

· финансирования экономических и инноваторских проектов;

· фьючерсных договоров и ряд остальных.

К задачкам прогнозирования на бирже можно отнести:

1. ­Прогнозирование короткосрочных и длительных тенденций. Задачей автоматической системы прогнозирования короткосрочных и длительных тенденций денежных рынков является анализ некого набора влияющих причин с следующим выводом о предстоящем короткосрочном либо длительном поведении предсказуемой величины. Вероятными предсказуемыми величинами для схожих систем являются доходность и ценовые характеристики: средневзвешенная стоимость, цены закрытия и открытия, наибольшая и малая цены. При этом прогнозироваться могут как характеристики, определенные для целой группы инструментов либо некого рынка в целом, так и характеристики, определенные лишь для 1-го инструмента денежного рынка. Как для совокупы инструментов, так и для всякого персонально может определяться доходность; ценовые характеристики определяются для всякого определенного инструмента. Целями прогноза (предсказуемой величиной) в области денежных рынков могут являться, к примеру, средневзвешенная доходность бескупонных облигаций (для группы инструментов), средневзвешенная стоимость акции, курс южноамериканского бакса к гривне и др. В качестве начальных данных (влияющих причин) для такового прогноза могут употребляться разные макро- и микроэкономические характеристики, информация с торговых площадок, данные, предоставляемые информационно-торговыми агентствами, экспертные оценки профессионалов. количество влияющих на прогноз причин зависит от рассматриваемого рыночного инструмента и определенной рыночной ситуации (временного момента). Другими словами одни причины оказывают воздействие на все денежные рынки, остальные – лишь на определенные. Не считая того, воздействие причин на рынки может изменяться с течением времени (изменяются рыночные тенденции). Потому что в определенные моменты времени выслеживается очевидная связь меж финансовыми рынками и инструментами рынков, целенаправлено в качестве начальных данных для прогнозирования 1-го рынка либо его инструментов употреблять информацию о тенденциях остальных рынков. К примеру, при прогнозировании цены открытия «сейчас» для всех инструментов всех денежных рынков, этот прогноз очень зависит от цены закрытия «вчера» и обе эти величины могут выступать как предсказуемые.

Прогнозирование короткосрочных и длительных тенденций фондового рынка включает последующие этапы.

1. Сбор и хранение статистических данных – вероятной начальной инфы для прогноза (или в качестве начальных данных, или в качестве предсказуемой величины, или как и то и это);

2. Определение для рассматриваемого рынка либо инструмента предсказуемой величины и набора влияющих причин (при этом не постоянно могут быть применены данные, конкретно хранящиеся в базе данных, часто требуется произвести некие преобразования данных: к примеру, нередко в качестве таковых причин употребляются относительные конфигурации величин);

3. Выявление зависимости меж предсказуемой величиной и набором влияющих причин в виде некой функции;

4. Вычисление интересующей величины в согласовании с определенной функцией, значениями влияющих причин на предсказуемый момент и видом прогноза (короткосрочный либо длительный).

Процедура выполнения короткосрочного прогноза различается от процедуры длительного на первом и четвертом шагах. В случае короткосрочного прогноза считается, что все участвующие в нем важные действующие причины на предсказуемую дату известны и хранятся в базе данных. Горизонт короткосрочного прогноза не превосходит 3–4 денька. В случае длительного прогноза считается, что важные действующие причины на предсказуемую дату неопознаны и должны быть указаны ожидаемые значения и погрешности. Соответственно погрешность определения предсказуемой величины значительно возрастает (чем далее горизонт прогноза, тем больше погрешность определения влияющих причин и возможность ошибки аналитика). Горизонт длительного прогноза, как правило, превосходит 3–4 денька.

2. Прогнозирование тенденций фондового рынка (рынка акций).

Принципиальная область внедрения нейронных сетей в сфере денег – прогнозирование ситуации на фондовом рынке. Обычный подход к решению данной для нас задачки (не использующий нейронные сети) базируется на агрессивно фиксированном наборе «правил игры», который со временем теряет свою актуальность из-за конфигурации критерий торгов на фондовой бирже. Кроме того, системы, построенные на базе такового обычного подхода, оказываются очень неспешными для ситуаций, требующих от трейдера (участника торгов) моментального принятия решений.

Разглядим, некие индивидуальности действий на фондовом рынке. Трейдер, принимающий решения о купле–продаже акций, имеет доступ к одному либо нескольким электрическим источникам инфы (Reuters, DowJonesTelerate, Bloomberg, Tenfore). Он следит текущие значения и графики интересующих его индексов на глобальных фондовых биржах, главные кросс-курсы валют и остальные характеристики денежного, фондового и кредитного рынков в многооконной среде с различной степенью детализации. На принятие его решения о купле–продаже акций, естественно, влияют макроэкономические и общественно-политические действия, сообщения о которых через любые 5–10 минут возникают в текстовом окне монитора и сопровождаются комментами профессионалов, озвучивающих различные слухи и прогнозы. Трейдеру также доступна доборная информация, таковая как сообщения из Государственного банка Украины и от остальных означающих источников о главных показателях рынков.

Непременно учитывается психология

Фондовый рынок характеризуется также последующими чертами:

-рыночные процессы очень неоднородны во времени: к примеру, состояние рынка в осеннюю пору значительно различается от его состояния в летнюю пору такого же года; потому не постоянно имеет смысл сформировывать обучающие подборки огромного размера;

-«загрязнениями» данных и их неоднородностью;

-наличием малоинформативных характеристик при относительно малом объеме статистики.

В целом, задачка короткосрочного прогноза котировок акций пусть и с

внедрением нейронных сетей представляется довольно сложной, в особенности на быстро изменяющемся украинском фондовом рынке.

Примером прогнозирования тенденций фондового рынка может служить нейросетевая система (компания Alela Corp.), созданная для прогноза конфигурации биржевых индексов Dow Jones, S&P500 и Merval. На веб-сайте компании можно безвозмездно пользоваться прогнозом конфигурации данных индексов и, используя его в качестве доборной инфы, убедиться, что толика верных прогнозов составляет не наименее 80,0 %.

Японские компании, оперирующие на рынке ценных бумаг, также обширно используют нейронные сети (компания Митсубиши). Для входа нейронной сети использовалась информация о деловой активности нескольких организаций, приобретенная за 33 года, включая также оборот, предшествующую стоимость акций, уровни дохода и т.д. Данная нейронная сеть самообучалась на настоящих примерах и показала высшую точность прогнозирования, также быстродействие. Общая результативность прогноза по сопоставлению с системами, использующими обычные статистические подходы, стала лучше на 19,0 %.

2.3. Ограничения и недочеты, связанные с внедрением нейронных сетей на бирже

1. Для действенного прогнозирования, как правило, нужен некий минимум наблюдений (наиболее пятидесяти и даже 100). Но существует много задач, когда такое количество статистических данных труднодоступно.

2. Остальным недочетом моделей на базе нейронных сетей являются значимые временные Издержки для заслуги удовлетворительного результата. Эта неувязка не настолько существенна, если исследуется маленькое число временных последовательностей, но обычно прогнозирующая система включает от нескольких сотен до нескольких тыщ временных последовательностей.

3. Научить и эксплуатировать нейронную сеть для решения почти всех задач, как правило, может и не спец, но накрепко интерпретировать результаты, также численно оценивать значимость получаемых прогнозов способны спецы, имеющие способности в моделировании нейронных сетей.

Разглядим также ряд особенностей и затруднений, связанных с внедрением программных товаров нейросетевого моделирования:

1. На фондовом рынке только немногие из профессионалов удачно управляются с действенной настройкой нейросимуляторов в особенности в тех вариантах, когда к прогнозированию приходится завлекать малозначимые действующие причины и требуется верно интерпретировать результаты опции нейронной сети. Для действенного использования нейросимуляторов нужно также отлично осознавать суть моделируемого процесса.

2. При использовании нейронной сети нужно учесть воздействие детерминированной повторяющейся функции именуемой в теории временных рядов «аддитивной сезонной компонентой» и определяемой способами спектрального анализа. Период сезонной составляющие составляет от 7 до 14 дней. Она может учесть, к примеру, то, что в 1-ые два–три денька всякого месяца обычно наблюдается локальный подъем котировок акций, а посреди месяца есть деньки, когда на валютный Рынок оказывают воздействие обязательства по договорам на куплю–продажу валюты по заблаговременно обсужденной стоимости и т. д. На шаге прогноза сезонная компонента может автоматом добавляться в одну из колонок электрической таблицы с данными и, таковым образом, учитываться в нейросимуляторе при оценке предсказуемого приращения котировок.

3. Практика работы с нейросимуляторами на финансовом рынке свидетельствует о том, что создание и тщательное ведение широкой, повсевременно обновляемой и отлично структурированной базы денежных, макроэкономических и политических данных очень принципиально, так как они значительно влияют на ситуацию и свойство прогноза. Потому что ситуация на рынке безпрерывно меняется, то и набор означающих влияющих причин (либо их порядок снутри этого набора) также меняется во времени. В связи с сиим, нейронную сеть нужно время от времени настраивать и учить поновой.

4. наличие подробной документации очень принципиально при работе с нейросимулятором. Документация обычно включает подробное описание способов и примеров, индексный и предметный указатели, также обучающий курс. Некие компании–создатели нейросимуляторов поддерживают «жаркую линию» по телефону и Веб, также проводят семинары юзеров по обучению приемам действенной работы с нейросимуляторами.

1.6. Задачи развития нейронных сетей

Разглядим ряд заморочек, стоящих сейчас на пути широкого распространения нейросетевых технологий.

1. Большая часть используемых нейронных сетей представляют сети оборотного распространения – более пользующегося популярностью современного метода. В свою очередь, метод оборотного распространения не волен от недочетов. До этого всего не существует гарантии, что нейронная сеть быть может обучена за конечное время: часто усилия и издержки машинного времени на обучение , пропадают зря. Когда это происходит, обучение повторяется – без всякой убежденности, что итог окажется лучше.

2. Нет также убежденности, что сеть обучится лучшим вероятным образом. метод обучения может попасть в «ловушку» так именуемого локального минимума ошибки, и лучшее решение не будет получено.

3. Создано много остальных алгоритмов обучения нейронных сетей, имеющих свои достоинства, но, необходимо подчеркнуть, что они все не свободны от ограничений.

4. Создатели склонны гиперболизировать свои успехи и замалчивать беды, создавая часто о нейронных сетях и нейрокомпьютерах необъективное воспоминание. Потому предприниматели, желающие основать новейшие компании в области нейросетевых технологий, должны максимально верно представлять пути развития того либо другого проекта и пути получения прибыли.

5. Таковым образом, существует опасность, что нейросетевые технологии начнут продаваться и покупаться ранее, чем придет их время, обещая потребительские и многофункциональные способности, которые пока нереально добиться. Если это произойдет, то разработка в целом может пострадать от утраты кредита доверия и возвратится к периоду невостребованности 70-х годов.

6. Существует неувязка неспособности обычных искусственных нейронных сетей «разъяснить», как они решают задачку. Это припоминает нашу неспособность разъяснить, как мы узнаем человека, невзирая на расстояние, освещение и прошедшие годы.

7. разработка просит улучшения имеющихся способов и расширения теоретических основ, для того чтоб нейронные сети вполне реализовали свои потенциальные способности.

8. До этого чем искусственные нейронные сети можно будет употреблять для решения задач, где поставлены на карту людские жизни либо принципиальные народнохозяйственные объекты, должны быть решены вопросцы надежности искусственных нейронных сетей.

Таковым образом, типовые задачки, решаемые при помощи нейронных сетей и нейрокомпьютеров последующие: автоматизация процесса систематизации; автоматизация прогнозирования; автоматизация процесса пророчества; автоматизация процесса принятия решений; управление; кодирование и декодирование инфы; аппроксимация зависимостей и др.

области внедрения нейронных сетей очень многообразны – это определение текста и речи, семантический поиск, экспертные системы и системы поддержки принятия решений, пророчество курсов акций, системы сохранности, анализ текстов. Одной из более сложных и нужных возможностей нейронных сетей является прогнозирование.

К задачкам прогнозирования на бирже можно отнести прогнозирование короткосрочных и длительных тенденций (сбор и хранение статистических данных; определение для рассматриваемого рынка либо инструмента предсказуемой величины и набора влияющих причин; вычисление интересующей величины в согласовании с определенной функцией, значениями влияющих причин на предсказуемый момент и видом прогноза), также прогнозирование тенденций фондового рынка.

Самые большие препядствия внедрения искусственных нейронных сетей (ИНС) соединены как с освоением непрофильными спецами базовых понятий ИНС, так и с освоением приемов нейросетевого моделирования специфичных для той либо другой задачки либо предметной области.

Отсутствие приспособленной документации и обучающего курса, включающие подробное описание способов и примеров, индексный и предметный указатели, значительно ограничивает применение ИНС на фондовой бирже.

В истинное время обучающие системы и тренажеры по применению ИНС фактически отсутствуют либо недосягаемы. Это обосновано тем, что методики использования ИНС очень разнообразны.

ГЛАВА 3. исследование ДИНАМИКИ ФИНАНСОВЫХ РЫНКОВ НЕЙРОСЕТЕВЫМИ МЕТОДАМИ

3.1. задачки и способы нейросетевого анализа и прогнозов

В истинной главе рассматриваются динамические процессы в 3-х секторах денежных рынков – денежном, валютном и серьезном.

В истинной работе мы не описываем шагов и способов данной для нас подготовительной обработки данных. Но подготовительный анализ дозволил улучшить характеристики нейросети, найти горизонт прогноза и провести сопоставление свойства пророчеств для временных рядов из разных секторов денежного рынка. А именно, для сопоставления свойства пророчества разных денежных рядов нейросетью одной и той же архитектуры мы нормировали начальные данные к схожей дисперсии.

Разглядим динамические процессы на денежном, валютном, серьезном рынках в короткосрочные периоды, прогнозируя дневную динамику способами нейронных сетей.

Анализируемые в реальном разделе денежные инструменты– это фьючерсы:

· на курс бакс США

Отметим две индивидуальности нейросетевого анализа. Если в данных, на которых училась нейросеть, не отражены ценовые конфигурации, обусловленные экзогенными факторами (начало, окончание войн, реформа денежной системы, нежданные результаты выборов президента, последствия террористических атак), то нейросеть не сумеет предсказать похожие ценовые конфигурации в дальнейшем. В то же время нейронные сети эффективны для пророчеств денежных крахов, паник, если они порождены эндогенными факторами (искаженное распространение инфы, рост курсов из-за огромных покупок, падения из-за огромных продаж, изменение ликвидности рынков, нелинейность корректировки курсов).

Итак, нейронные сети – это системы искусственного ума, способные к самообучению в процессе решения задач.

Обучение сводится к обработке сетью огромного количества примеров, состоящих из:

· набора пар входов и выходов (обучение с учителем) ;

· набора лишь входов (обучение без учителя).

В первом случае сеть по данным входам генерирует свои выходы и ассоциирует крайние с выходами из обучающего набора. Для максимизации выходов, попадающих в допустимый интервал отличия от обучающих, нейронная сеть видоизменит интенсивности связей меж нейронами, из которых она построена, и таковым образом самообучается. Прогонка обучающих примеров проводится, пока не достигается предпочитаемая точность совпадения настоящих и обучающих выходов. Отныне нейросеть считается обученной, и быть может использована к обработке данных, схожих на обучающие, но не совпадающие с ними.

Любой нейрон сети владеет своим весом (положительным, отрицательным) и так именуемой функцией активации. Нейрон обрабатывает входные сигналы, суммируя входы с весами и трансформируя приобретенный итог в выходной сигнал при помощи функции активации
линейной, нелинейной, стохастической). Нейроны сети ведут взаимодействие друг с другом зависимо от топологии связей. Крайние бывают полными (любой с каждым), частичными (противоположность полной связи), с петлями оборотных связей, без таких. В каждой задачке требуется собственный выбор архитектуры сети. наличие оборотных связей влияет на обучаемость сети (улучшая ее), тогда как степень внутренних связей описывает параллелизм вычислений. Современные мультислойные нейросети сильнее, а именно, из-за того, что они сформировывают внутреннее сеть «задумывается» о свойствах, содержащихся во входах.

Более пользующийся популярностью обучающий метод – это оборотное распространение ошибки, состоящее из взаимосвязанных действий. В прямом процессе входной сигнал проходит через сеть, генерируя определенный выход. В оборотном процессе ошибка (разница меж хотимым и приобретенным выходом) передается от выходных слоев к входным с одновременной модификацией связей нейронов так, чтоб (при следующем прогоне инфы через сеть) ошибка на выходном слое уменьшилась. В этом состоит обучение сети.

Опишем методику нейросетевого прогнозирования рассматриваемых в статье денежных инструментов.

Фуррор нейросетевых пророчеств зависит от типа инфы, подаваемой на вход, и от того, какие свойства выходных данных значимы в задачке прогноза. В построенной сети на один из входов подавались значения дневных доходностей анализируемых денежных инструментов, выраженные последующим образом: изменению 1,5 % соответствовало денек вспять сеть давала прогноз сглаженного 5-дневного среднего на один денек в будущее.

Из различных конфигураций нейросетей была выбрана рекуррентная нейросеть с оборотной связью от укрытого слоя ко входному (см. рис. 3.1).

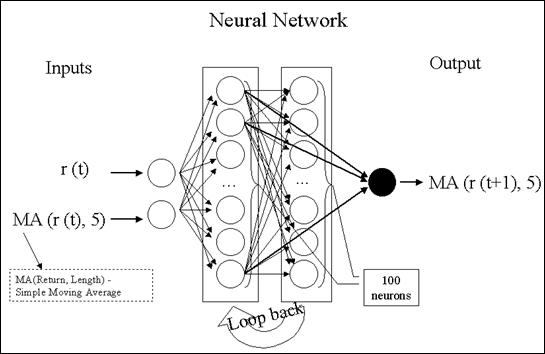
Рис. 3.1. Архитектура нейронной сети Элмана-Джордана, использованной для прогноза

Источник: составлена создателем по материалам [18, с. 145; 19, с 125]

Этот тип сетей с обучением способом оборотного распространения ошибки удачно употреблялся для пророчества денежных рынков, так как конкретно рекуррентная сеть выучивает закономерности в последовательности величин, что нужно для работы с временными рядами. Недочетом таковой сети является долгое время обучения. Послойные сети, обучаемые сиим способом, на любой схожий входной паттерн отвечают одним и этим же паттерном на выходе. Рекуррентные сети могут отвечать на один и этот же входной паттерн по-разному, зависимо от того, какой паттерн был предшествовавшим. Таковым образом, для их существенна последовательность обучающих примеров. Другими словами, рекуррентные сети могут быть обучены так же, как обычные сети с оборотным распространением ошибки, но обучающие примеры должны быть упорядочены и не могут предъявляться сети в случаем избранном порядке. Значимая разница с послойными сетями заключается в наличии у сети Элмана-Джордана доп блока, хранящего информацию о прошлых входах. Он быть может интерпретирован как блок длительной памяти нейросети.

Нейроны укрытого слоя сети Элмана-Джордана имеют логистическую функцию активации f(x)=1/(1+exp(-x)), тогда как нейроны выходного слоя владеют линейной функцией активации. Таковая композиция дозволяет аппроксимировать всякую функцию с конечным числом разрывов с данной точностью. Мы употребляли симметричную логистическую функцию активации f(x)=(2/(1+exp(-x)))-1. Это не влияло на предсказательные характеристики сети, но приводило к наиболее резвой сходимости метода обучения для данного типа временных рядов. На самом деле, единственным требованием к сети было достаточное число нейронов в сокрытом слое, так как их число обязано возрастать пропорционально трудности анализируемых данных (сложность данных оказалась таковой, что удалось ограничиться 100 нейронами в сокрытом слое).

Более сложным в использовании нейросетей является выбор момента остановки обучения. Если сеть учить недолго, то она не выучит подборку обучающих примеров. Если сеть учить очень длительно, то она выучит примеры с шумами со сколь угодно высочайшей точностью, но окажется неспособной обобщать примеры (т. е. будет действовать похожим образом на данных, не входивших в обучающее огромное количество). Для преодоления данной для нас трудности мы употребляли функцию калибровки с тем, чтоб улучшить сеть, применяя ее к независящему тестовому огромному количеству примеров в процессе обучения. Калибровка дозволяет отыскать оптимум нейросети на тестовом огромном количестве, означая способность сети к обобщению, т. е. получению добротных результатов на новейших данных. Это достигается вычислением среднеквадратичной ошибки меж настоящими и предсказанными выходами. Мы употребляли среднеквадратичную ошибку как обычную статистическую меру свойства фитирования.

3.2. Нейросетевые прогнозы доходностей

Опишем нужные технические детали, связанные с обучением и прогнозом использованной нами нейросети на обрисованных выше данных.

Из всякого временного ряда выделялось 3 подмножества:

· тренеровочное (примеры, на которых училась сеть) – 1-ые 900 значений для всех фьючерсов;

· тестовое (примеры, которые служили для предотвращения переучивания сети либо калибровки) – значения фьючерсных рядов с 901 по 1100;

· рабочее (примеры, которые сеть не лицезрела) – крайние 200 значений для фьючерсных временных рядов.

Результаты пророчества нейросетью рабочего огромного количества всех проанализированных временных денежных рядов приведены на рис. 3.2, 3.3, 3.4.

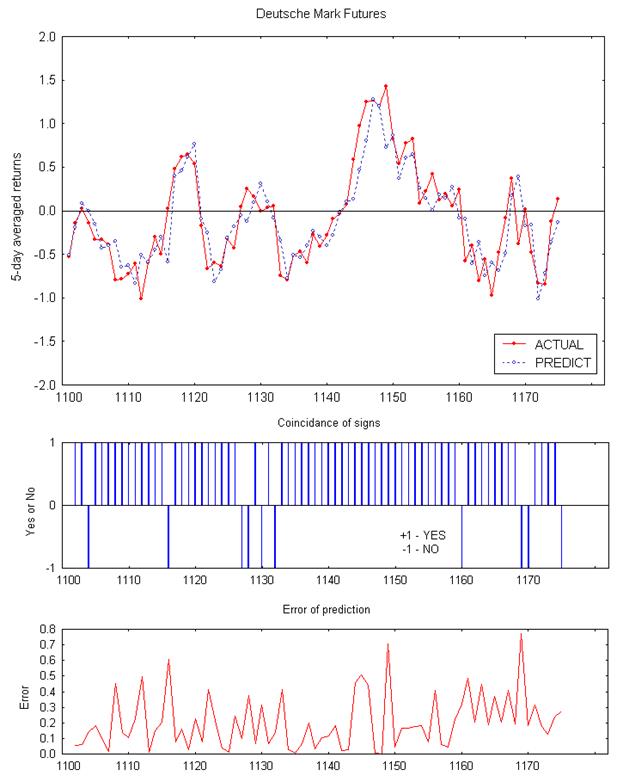
Рис. 3.2
Нейросетевые пророчества 5-дневных сглаженных относительных конфигураций котировки фьючерса на марку ФРГ – DM

Источник: составлена создателем

Верхний набросок – графики фактического и предсказанного нейросетью конфигураций, выраженных в процентах; набросок посреди – совпадение знака пророчества на любой денек; нижний набросок – модуль ошибки пророчества, выраженный в процентах. По горизонтальной оси отложены номера отсчетов (дней).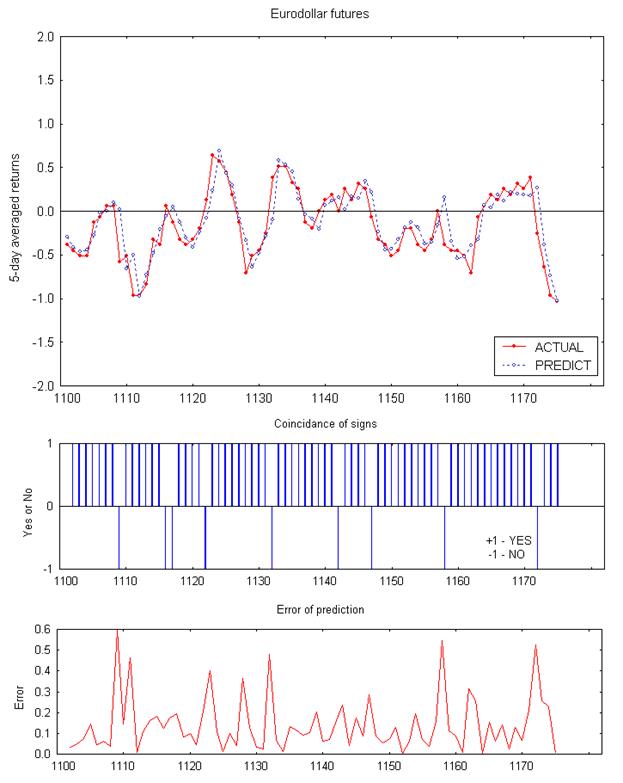

Рис. 3.3. Нейросетевые пророчества 5-дневных сглаженных относительных конфигураций котировки фьючерса на евродоллар – ED

Верхний набросок – графики фактического и предсказанного нейросетью конфигураций, выраженных в процентах; набросок посреди – совпадение знака пророчества на любой денек; нижний набросок – модуль ошибки пророчества, выраженный в процентах. По горизонтальной оси отложены номера отсчетов (дней).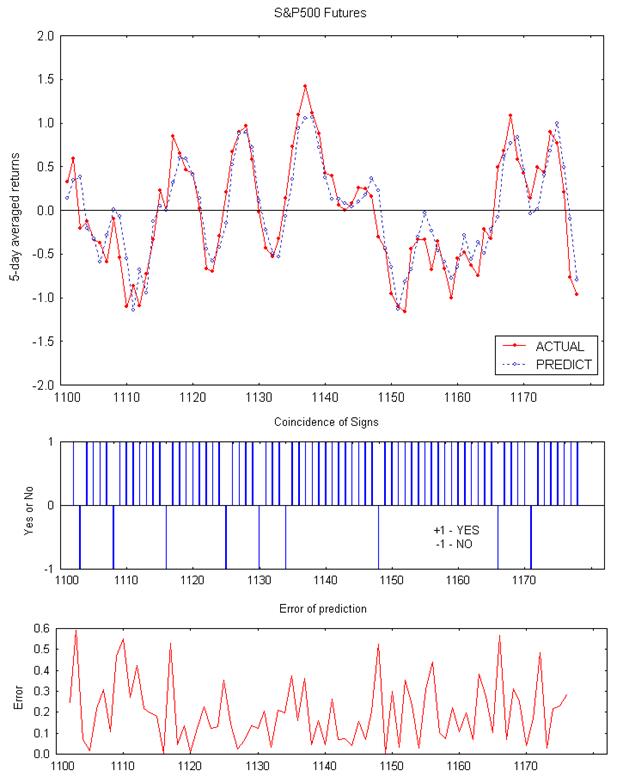

Рис. 3.4
Нейросетевые пророчества на рабочем огромном количестве 5-дневных сглаженных относительных конфигураций котировки фьючерса на биржевой индекс S&P500 – SP

Источник: составлена создателем

Верхний набросок – графики фактического и предсказанного нейросетью конфигураций, выраженных в процентах; набросок посреди – совпадение знака пророчества на любой денек; нижний набросок – модуль ошибки пророчества, выраженных в процентах. По горизонтальной оси отложены номера отсчетов (дней).

Эффективность пророчеств нейросети проверялась сопоставлением фактического значения и предсказанного нейросетью.

Аспектами свойства пророчества служили последующие характеристики:

Число эпох и время обучения – характеристики, как длительно сеть способна облагораживать пророчества на тестовом огромном количестве. Под эрой обучения соображают однократное предъявление сети набора обучающих примеров. Число эпох и время обучения изменяются зависимо от данных темпа обучения и момента, устанавливаемых из хотимой точности пророчества. Чем меньше их значения, тем наиболее точен итог и тем подольше учится нейросеть. В использованной сети оба параметра имели

Коэффициент Q ассоциирует точность нейросетевой модели с точностью модели, в какой пророчества схожи и совпадают со средним значением всех примеров. Для крайней модели коэффициент Q равен нулю. Самый наилучший итог достигается, если Q воспринимает

— r-квадрат – коэффициент детерминации, равный отношению дисперсии предсказанных значений к дисперсии фактических, демонстрируя, какая часть дисперсии предсказанных значений разъясняется уравнением регрессии.

— Средняя ошибка – усредненный по обработанным примерам модуль разности меж предсказанным и фактическим значениями.

— Наибольшая ошибка – это наибольший модуль разности меж предсказанным и фактическим значениями посреди всех обработанных примеров.

— % правильного пророчества знака конфигурации – это отношение числа примеров, для которых символ настоящего и предсказанного значения совпадают, и общего числа обработанных примеров, умноженное на 100.

Ниже с помощью их оценена эффективность нейросетевых пророчеств динамики фьючерсных котировок для SP, ED, DM. Результаты сведены в таблицу 1. Она состоит из 3-х блоков. 2-ой содержит статистику, относящуюся ко всем данным по трем временным рядам, а конкретно, к 1173 отсчетам для S&P500 и по 1170 отсчетов для марки ФРГ и евродоллара. 3-ий блок отражает статистику по рабочим огромным количествам: из 77 отсчетов для S&P500 и 74 отсчетов для марки ФРГ и евродоллара.

Таблица. 3.1.

Численные свойства свойства нейросетевого прогнозамеждународных денежных инструментов

черта свойства
Фьючерс на S&P500
Фьючерс на марку ФРГ
Фьючерс на евродоллар

Число эпох обучения
30512
6779
1873

время обучения (часов округло)
19
4
1

Число примеров для обучения
1173
1170
1170

Коэффициент

0,7408
0,7594
0,7436

r–квадрат
0,7431
0,7612
0,7452

Средняя ошибка, %
0,182
0,196
0,179


Ошибка, %
2,172
1,291
2,281

% правильных пророчеств знака конфигурации
86
83
83

Число примеров для пророчеств
77
74
74

Коэффициент

0,8032
0,5897
0,4517

r–квадрат
0,8062
0,6319
0,5697

Средняя ошибка, %
0.217
0,279
0,201


Ошибка, %
0.799
1,046
1,234

% правильных пророчеств знака конфигурации
88
86
88

Источник: составлена создателем.

Мы лицезреем, что из 3-х проанализированных фьючерсных котировок лучшие пророчества достигаются на S&P500, наихудшие – на евродолларе, промежные — для марки ФРГ. Это следует из значений коэффициента
на рабочем огромном количестве (см. нижний блок табл.1), хотя зрительно на рис. 2а, 2b и 2c отличие в качестве прогнозов увидеть давольно тяжело. Необходимо подчеркнуть, что невзирая на однообразное свойство обучения нейросети на SP, ED, DM (см. значения коэффициента
в первом блоке табл.1), сеть училась на SP в 5 раз подольше, чем на DM, а на DM – в 4 раз подольше, чем на ED. Это, по-видимому, значит, что отыскать сокрытые закономерности, содержащиеся во фьючерсных котировках на SP, существенно труднее, чем надлежащие закономерности в DM и тем наиболее в ED. В то же время, как отмечено выше, лучшее свойство прогноза достигается как раз на SP, а наихудшее – на ED. Все совместно это свидетельствует о том, что сокрытые закономерности, обнаруженные нейросетью в SP, сохраняют собственный нрав на наиболее долгих интервалах времени по сопоставлению с ED либо, другими словами, фьючерсы на ED наиболее подвержены смене внутренних закономерностей, что и приводит к наихудшему качеству прогноза.

Таковым образом, отражая современные тенденции в финансовом мире, междисциплинарный подход в экономике и денег является прорывом в комбинировании разных способов теории трудности, таковых, к примеру, как способы нелинейной и хаотической динамики, мультифрактальный анализ и нейротехнологии. Интегральной задачей этого синтеза является , развитие и построения адаптивных умственных систем, помогающих практикам выигрывать в твердой конкурентноспособной среде.

В главе 3 рассмотрены динамические процессы на денежном, валютном, серьезном рынках в короткосрочные периоды, спрогнозирована дневная динамика способом нейронных сетей.

Анализируемые в реальном разделе денежные инструменты– это фьючерсы:

· на курс бакс США

Эффективность пророчеств нейросети проверялась сопоставлением фактического значения и предсказанного нейросетью. Из 3-х проанализированных фьючерсных котировок лучшие пророчества достигаются на S&P500, наихудшие – на евродолларе, промежные — для марки ФРГ.

ЗАКЛЮЧЕНИЕ

В истинное время искусственные нейронные сети уже дозволили совладать с непростых заморочек и обещают создание новейших программ и устройств, способных решать задачки, которые пока под силу лишь человеку. Современные нейрокомпьютеры употребляются в главном в программных продуктах и потому изредка используют собственный потенциал «параллелизма». Эра реальных параллельных нейровычислений начнется с возникновением на рынке огромного числа аппаратных реализаций – специализированных нейрочипов и плат расширений, созданных для обработки речи, видео, статических изображений и остальных типов образной инфы.

Огромное количество надежд в отношении нейронных сетей сейчас связывают конкретно с аппаратными реализациями, но пока время их массового выхода на рынок, видимо, еще не пришло. Они либо выпускаются в составе специализированных устройств, либо довольно дороги, а часто и то и это. На их разработку тратится существенное время, за которое программные реализации на самых крайних компах оказываются только на порядок наименее производительными, что делает внедрение нейропроцессоров невыгодным. Но все это лишь вопросец времени – нейронным сетям предстоит пройти этот же путь, по которому еще совершенно не так давно развивались компы, увеличивая свои способности и производительность, захватывая новейшие сферы внедрения по мере появления новейших задач и развития технической базы для их разработки.

должен поменяться и интерфейс взаимодействия юзера с сетью, который будет основываться на умственных агентах – новеньком виде программного обеспечения, получившем заглавие «Agentware». Агенты будут вести взаимодействие не только лишь со своим юзером, да и с иными таковыми же агентами и со особыми сервисами. Вследствие этого в сети покажется собственного рода новейший социум с самообучающимися агентами, которые будут принимать решения от имени юзера, и еще пока тяжело сказать, к чему это приведет.

В качестве подведения итогов хотелось бы сказать, что сейчас нейронные сети уже не являются уделом маленькой группы теоретиков. К нейросетевым приложениям подключаются инженеры и исследователи различных специальностей. В особенности веселит прогресс в построении успешных нейросетевых моделей исследуемых явлений, вполне базирующихся на экспериментальных данных. тут более много появляются примечательные характеристики искусственных нейронных систем: мощная параллельность обработки инфы, ассоциативность памяти и способность к обучению на опыте. Это открывает новейшие перспективы для классификации бессчетной экспериментальной инфы в таковых областях познаний, где обычно тяжело приживается математический формализм, к примеру, в медицине, психологии и истории.

В процессе выполнения данной курсовой работы была достигнута цель исследования, а конкретно исследовано применение нейронных сетей к задачкам биржевой деятель. Также были удачно решены поставленные задачки: ознакомление со структурой нейронных сетей, правилами и принципами их функционирования. В практической части была подтверждена эффективность внедрения нейронных сетей к более нужной задачке биржевой деятель ­– прогнозированию.

В последующих исследовательских работах нужно выполнить расширение круга поставленных перед искусственной нейронной сетью задач, что может отыскать практическое применение в экономической деятель субъектов хозяйствования.

СПИСОК ИСТОЧНИКОВ

1. Бобин А. Ю., Восьмирко С.О., Зубов М.Е. Программное обеспечение способа экстраполяции измерительных данных на базе нейронной сети. Радиотехника, электротехника и энергетика. – М.: Издательство МЭИ, 2003. – 388 с.

2. Богославский С.Н. Область внедрения искусственныхнейронных сетей иперспективы их развития. – М.: Издательство МЭИ, 2003. – 388 с.

3. Горбань А. Н., Россиев Д. А. Нейронные сети на индивидуальном компе. – Новосибирск.: Наука, 2006. – 289 с.

4. Ежов А.А., Шумский С.А. Нейрокомпьютинг и его внедрения в экономике и бизнесе. – М.: Издательство МЭИ, 2007. – 556 с.

5. Крисилов В.А., Олешко Д.Н., Трутнев А.В. Применение нейронных сетей в задачках умственного анализа инфы // Труды Одесского политехнического института. – 2007. – № 2.– С. 148-152.

6. Круг П.Г. Нейронные сети и нейрокомпьютеры: Учебное пособие по курсу «Процессоры». – М.: Издательство МЭИ, 2002. – 176 с.

7. Малинецкий Г.Г., Потапов А.Б. Русла и джокеры: о новейших способах прогноза поведения сложных систем. – М.: Издательство МЭИ, 2007. – 486 с.

8. Малинецкий Г.Г., Потапов А.Б. Современные препядствия нелинейной динамики. – М.: Издательство МЭИ, 2007. – 686 с.

9. Мариуца О.В., Колнаузов Е.С. Богданов А.В. Дегтярев А.Б. Информационно-аналитическое обеспечение проектирования систем поддержки принятия решений для денежных рынков. – С.-П., 2007. – 545 с.

10. Садовой А. В. Нейронные сети. STATISTICA Neural Networks. – М., 2004. – 582 с.

11. Сотник С. Л. методы обучения нейронных сетей грядущего. – М., 2006. – 481 с.

12. Уоссермен Ф. Нейрокомпьютерная техника. – М.: Мир, 2003. – 258 с.

13. Baestaens D.E., Den Bergh W.-M.Van, Wood D. Neural Network solutions for trading in financial markets. Pitman Publishing, 2004. – 545 р.

14. Cassetti M.D. A neural Network system for reliable trading signals, Stocks&Commodities, 2003. – 645 р.

15. Cont R., Scaling and correlation in financial data, 2007. – 265 р.

16. Giles C.L., Lawrence S., Tsoi A.Ch., Rule inference for financial prediction using recurrent neural networks, 2006. – 365 р.

17. Hecht-Nielsen R., Neurocomputing.: Addison-Wesley Publishing Company, Inc., 2007. – 456 р.

18. Moody J., Liao, Y., Saffel, M. Performance Function and Reinforcement Learning for Trading Systems and Portfolios // Journal of Forecasting. – 2007. – № 17. – Р. 441-470.

19. Prokhorov D., Puskorius G., Feldkamp L. Dynamical Neural Networks for Control. In J. Kolen and S. Kremer (eds.) A Field Guide to Dynamical Recurrent Networks. – L.: IEEE Press, 2004. – P. 23-78.

]]>