Учебная работа. Реферат: Исследование электрических колебаний (№27)

Учебная работа. Реферат: Исследование электрических колебаний (№27)

Нижегородский государственный Технический Университет.

Лабораторная работа по физике №2-27.

исследование электрических колебаний
.

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы:
экспериментальное исследование собственных и вынужденных колебаний тока и напряжения на элементах в колебательном контуре; измерение параметров контура: индуктивности
L
, сопротивления
R
, добротности
Q
; исследование прохождения синусоидального тока через
LCR
-цепь.

Теоретическая часть.

Рисунок 1.

Уравнение, которому удовлетворяет ток I в колебательном контуре (рис.1) с подключенным к нему генератором синусоидальной ЭДС e
=
e
0

×
cos
w
t
имеет вид: (1)

где:

— коэффициент затухания.

— собственная круговая частота, R — сопротивление резистора, L — индуктивность катушки, С — емкость конденсатора, ; e0
, w — амплитуда и круговая частота синусоидальной ЭДС.

Общее решение неоднородного линейного уравнения (1):

(2)

где: — круговая частота собственных затухающих колебаний тока.

и — начальные амплитуда и фаза собственных колебаний.

I
0
— амплитуда вынужденных колебаний тока.

Dj
—
разность фаз между ЭДС и током.

(3)

(4)

— импеданс цепи.

— индуктивное сопротивление, — емкостное сопротивление.

Собственные колебания:

Если b2
, то w¢ — действительная и собственная частота колебаний представляет собой квазипериодический процесс с круговой частотой w¢, , периодом , и затухающей амплитудой (рис 1).

За характерное время (t — время релаксации) амплитуда тока уменьшается в е

раз, то есть эти колебания практически затухают.

— добротность контура.

Если b2
³w0
2
, то w¢ — мнимая частота, и колебания представляют собой апериодический процесс.

— критическое сопротивление.

Вынужденные колебания:


c течением времени первый член в формуле (2) обращается в ноль и остается только второй, описывающий вынужденные колебания тока в контуре.

— амплитуда вынужденных колебаний напряжения на резисторе R.

При совпадении частоты ЭДС с собственной частотой контура (w=w0
), амплитуды колебаний тока и напряжения UR
0
на резисторе максимальны. большой селективный отклик колебательной системы на периодическое внешнее воздействие называется резонансом
.

Экспериментальная часть.

Результаты эксперимента:

№

f
, кГц

e
ЭФ

, мВ

UR

ЭФ

, мВ

a

b

,
×
10-4

D
j

,
°

1

180
200
24
4,0
3,4
1,2
58

2

190
190
32
5,2
4,0
1,7
51

3

195
185
38
6,0
4,3
2,0
48

4

200
180
45
2,8
2,0
2,5
46

5

205
170
54
3,2
2,0
3,2
38

6

210
155
63
3,8
2,0
4,1
32

7

215
142
72
4,2
1,0
5,1
14

8

218
138
75
4,4
0,0
5,4
0

9

220
135
76
4,3
0,5
5,6
6

10

225
140
73
4,2
1,8
5,2
25

11

230
150
65
3,8
2,6
4,3
43

12

235
165
56
3,5
2,6
3,4
48

13

240
175
48
3,0
2,7
2,7
64

14

250
180
36
2,2
2,1
2,0
76

15

260
195
28
1,8
1,7
1,4
90

16

270
200
22
1,6
1,6
1,1
90

17

280
200
18
1,3
1,3
0,9
90

18

290
200
15
1,0
1,0
0,8
90

19

300
205
12
1,0
1,0
0,6
90

Задание 1.
исследование зависимости амплитуды вынужденных колебаний от частоты (резонансная кривая).

исходные данные:Uвых
=200 мВ, eЭФ
=200 мВ. f
Î[180;300] кГц.

Расчеты необходимых величин:

1. f
0
= 220 кГц — частота резонанса.

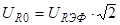
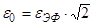
Строим график зависимости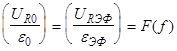

,где w1
и w2
— значения частот на уровне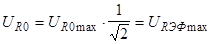

Из экспериментального графика видно, что он по своей форме совпадает с графиком, полученным теоретически из формулы: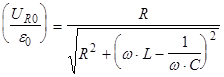

исследование зависимости разности фаз между ЭДС и током в контуре.

Из экспериментального графика Dj=F(f
) получаем: f
0
=218 кГц.

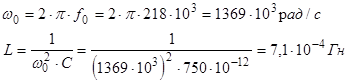
Сравнивая полученные результаты с результатами из предыдущего опыта видно, что различие в величинах w0
и L незначительны.

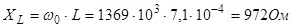
Можно сделать вывод, что при резонансной частоте XL
»XC
и величина импеданса цепи минимальна.

Рисунок 2.

Задание 2.
Исследование собственных электрических колебаний.

На данном рисунке представлена форма затухающих колебаний напряжения UC
на конденсаторе, полученная с помощью осциллографа. Изображение совпадает с теоретическим графиком.

Из графика: Т=2×2,4×10-6
с — период колебаний.

t=2×3,8×10-6
с — время релаксации.

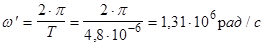
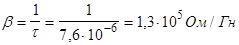
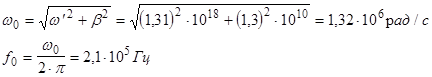
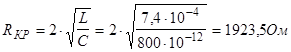
Задание 3.
Исследование прохождения синусоидального тока через
LCR
— цепь

.

f

,кГц

U
ВЫХЭФ

,10-3
В

U
0ВЫХ

,
10-3

В

150
41
56

160
33
46

170
27
38

180
22
31

190
14
19

200
9
13

205
6
8

210
3
4

215
1
2

218
0
0

220
0
0

225
1
2

230
2
3

235
4
6

240
5
7

250
9
13

260
13
18

270
17
24

280
22
31

290
25
35

300
30
42

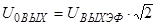
Построим график U0ВЫХ
=F(f
). Резонансная частота из графика равна: f
0
=220 кГц.

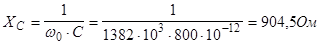
При этом импеданс цепи является бесконечно большим и ток в цепи не протекает.

R=50 Ом, f
=2 МГц.

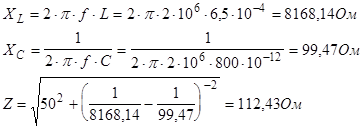
Погрешности измерений.

Задание 1.

1) Погрешностьf
0
:f
определяли на частотомере

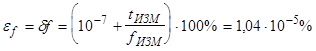
2) Погрешность L:

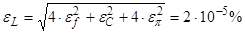
3) Погрешность Q:

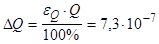
4) Погрешность R:

eR
=5% DR=3,1Ом

5) Погрешность XL
:

6) Погрешность XC
:

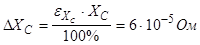
7) Погрешность b
:

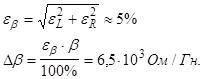
Вывод:

на этой работе мы экспериментально исследовали собственные и вынужденные колебания тока и напряжения на элементах в колебательном контуре; измерили параметры контура: индуктивности
L
, сопротивления
R
, добротности
Q
; исследовали прохождение синусоидального тока через
LCR
-цепь.