Учебная работа. Реферат: Математика в химии и экономике

Учебная работа. Реферат: Математика в химии и экономике

Реферат по арифметике ученицы 8 г класса Низовой Юлии

Городское образовательное учреждение – гимназия № 47

г. Екатеринбург, 2000

Введение

В школьном курсе арифметики достаточно не много внимания уделяется задачкам на консистенции, концентрации смесей и производительности труда. Но в крайние годы на вступительные экзамены в ВУЗы такие задачки даются абитуриентам довольно нередко и вызывают у их затруднения.

Цель реального реферата – исследование способов решения таковых задач, решение нескольких задач на изменение концентраций и на начисление обычных и сложных процентов.

Не считая того, так как в истинное время научная работа невообразима без компа я поставила для себя доп задачку освоить текстовый редакторWord, который употребляется более обширно.

задачки на концентрации

Рассматривая задачки на составление уравнений, остановимся, до этого всего, на задачках, решение которых соединено с внедрением понятий “концентрация” и “процентное содержание”. Обычно в критериях таковых задач речь идет о составлении сплавов, смесей либо консистенций 2-ух либо нескольких веществ.

Главные допущения, которые принимаются в задачках подобного рода, состоят в последующем:

а) все получающиеся сплавы либо консистенции однородны;

б) при слиянии 2-ух смесей, имеющих объемы V1
и V2
, выходит смесь, размер которой равен V1
+V2
, т.е. V0
=V1
+V2
.

Заметим, что такое допущение не представляет собой законфизики и не постоянно производится в реальности. По сути при слиянии 2-ух смесей не размер, а масса либо вес консистенции приравнивается сумме масс либо весов составляющих ее компонент.

задачки на смешивание при кажущейся простоте не являются явными. Так, в учебнике алгебры создателей Ш.А.Алимова, Ю.М.Колягина и др. в задачке

№ 491 допущена ошибка, которая не исправлена даже в 6 издании. текст задачки говорит: “Два раствора, из которых 1-ый содержит 0,8 кг, а 2-ой 0,6 кг безводной серной кислоты, соединили вкупе и получили 10 кг новейшего раствора серной кислоты. Отыскать массу первого и второго смесей в консистенции, если понятно, что !!!безводной серной кислоты в первом растворе было на 10% больше, чем во 2-м.” Если считать условие, выделенное курсивом верным, то

0,2 кг (0,8-0,6) безводной серной кислоты равно 10%, другими словами, 100% ее равно 2 кг, а по условию задачки ее всего в обоих смесях 1,4 кг (0,8+0,6). Противоречие исчезает, если заместо символов !!! вставить слово “концентрация”.

Разглядим для определенности смесь 3-х компонент А, В и С. Размер консистенции V0
складывается из размеров незапятнанных компонент:

V0
=VА
+VВ
+VС
,

а три дела

cA
=VА
/V0
, cB
=VB
/V0
, cC
=VC
/V0

демонстрируют, какую долю полного размера консистенции составляют объемы отдельных компонент:

VА
=cA
V0
, VB
=cB
V0
, VC
=cC
V0
.

Отношение размера незапятанной составляющие (VА
) в растворе ко всему размеру консистенции (V0
):

cA
=VА
/V0
=VА
/(VА
+VВ
+VС
)

именуется большой концентрацией данной составляющие.

Концентрации — это безразмерные величины; сумма концентраций всех компонент, составляющих смесь, разумеется, равна единице:

cA
+cB
+cC
=1.

Потому, для того чтоб структура раствора, состоящего из n компонент, была определена, довольно знать концентрацию (n-1)-й составляющие. Если известны концентрации сA
, сB
исC
компонент, составляющих данную смесь, то ее размер можно поделить на объемы отдельных компонент (рис. 1):

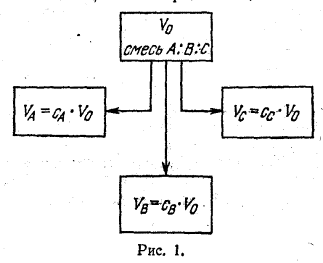
V0
=cA
V0
+cB
V0
+cC
V0
. (формула 1)

Большим процентным содержанием составляющие А именуется величина

рА
=cA
100% ,

т. е. концентрация этого вещества, выраженная в процентах.

Если понятно процентное содержание: вещества А, то его концентрация находится по формуле

cA
=рА
/100% .

Так, к примеру, если процентное содержание составляет 70%, то соответственная концентрация равна 0,7. Процентному содержанию 10% соответствует концентрация 0,1 и т.д.

Таковым же методом определяются и весовые (массовые) концентрация и процентное содержание, а конкретно как отношение веса (массы) незапятнанного вещества А

в сплаве к весу (массе) всего сплава. О какой концентрации, большой либо весовой, идет речь в определенной задачке, постоянно ясно из ее условия.

Встречается сравнимо мало задач, в каких приходится пересчитывать объемную концентрацию на весовую либо напротив. Для того чтоб это создать, нужно знать удельные веса компонент, составляющих раствор либо сплав. Разглядим для примера двухкомпонентную смесь с большими концентрациями компонент с1
и с2
(с1
+с2
=1) и удельными весами компонент d1
и d2
. Вес консистенции быть может найден по формуле

G=V1
d1
+V2
d2

в какой V1
и V2
— объемы составляющих смесь компонент. Весовые концентрации компонент находятся из равенств

k1
=V1
d1
/ (V1
d1
+V2
d2
)=c1
d1
/(c1
d1
+c2
d2
)=c1
d1
/(c1
(d1
-d2
)+d2
) ,

k2
=V2
d2
/ (V1
d1
+V2
d2
)=c2
d2
/(c1
d1
+c2
d2
)=c2
d2
/(d1
+c2
(d2
-d1
)) ,

которые определяют связь этих величин с большими концентрациями.

Как правило, в критериях задач рассматриваемого типа встречается один и этот же циклический элемент: из 2-ух либо нескольких консистенций, содержащих составляющие A1
, А2
, А3
, …, An
, составляется новенькая смесь методом перемешивания начальных консистенций, взятых в определенной пропорции. При всем этом требуется отыскать, в котором отношении составляющие A1
, А2
, А3
, …, An
войдут в получившуюся смесь.

Для решения данной задачки комфортно ввести в рассмотрение объемное либо весовое количество каждой консистенции, также концентрации составляющих их компонент A1
, А2
, А3
, …, An
. При помощи концентраций необходимо “расщепить” каждую смесь на отдельные составляющие, как это изготовлено в формуле (1), а потом обозначенным в условии задачки методом составить новейшую смесь. При всем этом просто подсчитать, какое количество каждой составляющие заходит в получившуюся смесь, также полное количество данной консистенции. Опосля этого определяются концентрации компонент A1
, А2
, …, An
в новейшей консистенции.

Проиллюстрируем произнесенное выше на примере последующей задачки.

задача1. Имеются два кусочка сплава меди и цинка с процентным содержанием меди р% и q% соответственно. В котором отношении необходимо взять эти сплавы чтоб, переплавив взятые кусочки вкупе, получить сплав, содержащий r% меди?

Решение. Составим иллюстративный набросок к данной задачке (рис. 2). Концентрация меди в первом сплаве равна р/100, во 2-м сплаве q/100.

Если первого сплава взять х кг, а второго у кг, то при помощи концентраций (ясно, что речь идет о весовых концентрациях) можно “расщепить” эти количества на отдельные составляющие:

х=хр/100 (кг меди) +x(1-p/100) (кг цинка)

и

y=yq/100 (кг меди) +y(1-q/100) (кг цинка).

количество меди в получившемся сплаве равно

хр/100+yq/100 (кг меди),

а масса этого сплава составит х+у кг. Потому новенькая концентрация меди в сплаве, согласно определению, равна

(хр/100+yq/100)/(х+у) .

По условию задачки эта концентрация обязана приравниваться r/100:

(хр/100+yq/100)/(х+у)=r/100 ,

либо

(хр+yq)/(х+у)=r .

Решим приобретенное уравнение. До этого всего заметим, что уравнение содержит два неведомых х и у. Несложно осознать, что оба неведомых совершенно точно не находятся. Концентрация получающегося сплава определяется не массой взятых кусков, а отношением этих масс. Потому в задачке и требуется найти не сами величины х и у, а лишь их отношение.

Отметим попутно, что выражение вида

F(x,y)=(ax+by)/(cx+dy) ,

называемое дробно-линейной функцией, нередко встречается в задачках на составление уравнений. В числителе и знаменателе данной дроби стоят линейный однородные выражения, зависящие от х и у. Если не разглядывать вариант у=0, то функция F(x,у) зависит практически лишь от одной переменной, а конкретно от дела x/y :

F(x,y)=(ax/y+b)/(cx/y+d)=j(x/y)

При всем этом уравнение F(x,y)=С дозволяет отыскать это отношение.

Запишем уравнение задачки в последующем виде:

x(p-r)=y(r-q) .

Разглядим вероятные случаи:

1) p=r=q .

В этом случае концентрации всех сплавов схожие и уравнение указывает, что имеется бессчетное огромное количество решений. Можно взять сколько угодно первого сплава и сколько угодно второго сплава.

2) p=r¹q .

В этом случае уравнение приобретает вид

х x 0=у(r-q),

откуда находим: х — хоть какое, у=0. Физический смыслу этого решения понятен: если концентрация сплава, который требуется получить, совпадает с концентрацией первого сплава, но не равна концентрации второго сплава, то первого сплава можно взять сколько угодно, а второго сплава не брать совсем.

3) p¹r=q .

Получаем уравнение

x(p-r)=y x 0

откуда находим: у — хоть какое, х=0.

4) p¹r , p¹q , r¹q .

В этом случае можно написать

x=y(r-q)/(p-r) .

Так как у¹0, то

x/y = (r-q)/(p-r) .

Это

(r-q)/(p-r)>0

которое, как несложно показать, имеет пространство, если

Невзирая на то, что этот пример очень обычной, он довольно отлично иллюстрирует главный способ решения задач, связанных со растворами. Разглядим еще одну задачку.

задачка 2. Три схожие пробирки заполнены до половины смесями спирта. Опосля того как содержимое третьей пробирки разлили поровну в 1-ые две, большая концентрация спирта в первой уменьшилась на 20% от начальной, а во 2-ой возросла на 10% от начального значения. Во сколько раз первоначальное количество спирта в первой пробирке превышало первоначальное количество спирта во 2-ой пробирке?

Решение. Введем в рассмотрение размер половины пробирки V0
и концентрации смесей спирта в каждой из пробирок с1
, с2
и с3
. Тогда первоначальное количество спирта в первой пробирке равно V0
с1
, во 2-ой V0
с2
, в третьей V0
с3
(рис. 3).

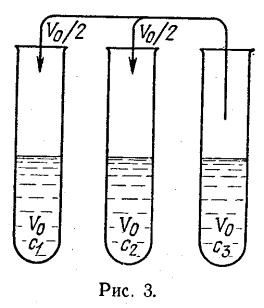
Для того чтоб решить задачку, подсчитаем количество спирта в первой и 2-ой пробирках опосля того, как туда добавят содержимое третьей пробирки. Эти количества будут равны:

в первой пробирке

V0
с1
+1/2 V0
c3
,

во 2-ой пробирке

V0
с2
+1/2 V0
c3
.

Найдем новейшие концентрации спирта в этих пробирках. Для первой пробирки она равна

с1
=V0
с1
+1/2 V0
c3
/ 3/2 V0
,

для 2-ой

с2
=V0
с2
+1/2 V0
c3
/ 3/2 V0
.

По условию задачки с1
*
=0,8c1
и с2
*
=1,1с2
, Тогда имеем систему 2-ух уравнений с 3-мя неведомыми:

2/3 c1
+1/3 c3
=0,8c1
,

2/3 c2
+1/3 c3
=1,1c2
,

либо

2c1
-5c3
=0 ,

13c2
-10c3
=0 .

Из данной системы, так же как и в предшествующей задачке недозволено найти все три концентрации с1
, c2
и c3
. Но благодаря тому, что уравнения системы представляют собой однородные линейные выражения, из нее можно отыскать дела 2-ух концентраций к третьей к примеру, с1
/с3
и с2
/с3
:

m=с1
/с3
=5/2 , n=с2
/с3
=10/13 .

количество спирта в первой пробирке относится к количеству спирта во 2-ой пробирке, как m/n. Вправду,

V0
с1
/V0
с2
=m/n=13/4 .

Потому ответ в данной задачке таковой: 13:4.

Обратимся сейчас к задачкам, которые можно соединить в одну группу из-за того, что их решение соединено с выявлением общей закономерности конфигурации той либо другой величины в итоге неоднократно циклической операции.

Разглядим последующий пример.

задачка 3. В сосуде, размер которого равен V0
л, содержится р%-ный раствор соли (рис. 4). Из сосуда выливается, a л консистенции и доливается а л воды, опосля что раствор перемешивается. Эта процедура повторяется n раз. Спрашивается, по какому закону изменяется концентрация соли в сосуде, т.е. какова будет концентрация соли опосля n процедур?

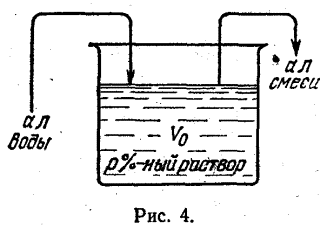
Решение. Разумеется, что первоначальное количество соли в растворе равно

p/100 x V0
.

Опосля того как отлили а л консистенции, в растворе осталось

p/100 x V0
— p/100 x a = p/100 x V0
(1-a/V0
)

соли, а ее концентрация опосля прибавления а л воды стала равной

c1
= p/100 х (1-a/V0
) .

Опосля того как отлили еще а л консистенции (но уже с концентрацией c1
), в растворе осталось соли

1/100 х V0
(1-a/V0
)-c1
a= p/100 х V0
(1-a/V0
)2
,

а ее концентрация опосля прибавления а л воды стала равной

c2
=p/100 х (1-a/V0
)2
.

Нет надобности снова проделывать ту же функцию, чтоб убедиться, что концентрация соли в растворе опосля n переливаний определяется формулой

cn
=p/100 (1-a/V0
)n
, (формула 2)

А сейчас решим несколько задач.

1. Задачка на разбавление.

Из сосуда, заполненного кислотой, вылили несколько л. и долили водой; позже снова вылили столько же л. консистенции, тогда в сосуде осталось 24л незапятанной кислоты. Емкость сосуда 54л. Сколько кислоты вылили в 1-ый и 2-ой раз?

Решение.

Пусть впервой вылили х л. кислоты. Тогда в сосуде осталось 54-х л. кислоты. Во 2-ой раз вылили х л. раствора кислоты концентрации

100(54-х)/54%., другими словами в этом растворе было х(54-х)/54 незапятанной кислоты. Другими словами

х+х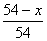=54-24

54х +54х-х2
=5430

х2
– 108х + 1620 = 0

х1
=90-не удовлетворяет условию задачки

х2
= 18

Как следует, впервой вылили 18л кислоты, во 2-ой раз – 12л.

2. задачка на смешивание. (задачка № 491)

Условие приведено на стр.4.

Пусть х – масса 1-го раствора, тогда концентрация его 0,8/х, масса второго раствора 10-х, концентрация второго раствора 0,6/(10-х). Как следует,

— = 0,1

0,8(10-х) – 0,6х = 0,1х(10-х)

х=20- не удовлетворяет условию задачки

х=4

Как следует, масса первого раствора 4 кг, масса второго раствора 6 кг.

Задачки на банковские проценты:

За хранение сбережений вкладчика и разрешение распоряжаться этими средствами средств. Зависимо от метода начисления проценты делятся на обыкновенные и сложные.

1. Обыкновенные проценты.

Повышение вклада S0
по схеме обычных процентов характеризуется тем, что суммы процентов в течение всего срока хранения определяются исходя лишь из начальной суммы вклада независимо от срока хранения и количества периодов начисления процентов. Пусть вкладчик открыл счет и положил на него S0
рублей. Пусть банк обязуется выплачивать в конце всякого года р% от начальной суммы S0.
Тогда по истечении 1-го года сумма начисленных процентов составит руб., и величина вклада станет равной S1
=S0
. Величину р % именуют годичный процентной ставкой. Если бросить вклад еще на год, то начисление процентной ставки делается на начальный вклад S0
и не делается на величину. Другими словами, через n лет сумма начисленных процентов составит Пn
= руб., а величина вклада вкупе с процентами составит Sn
= S0
руб. (формула 3). Отношение Sn
/S0
именуют коэффициентом наращивания обычных процентов.

Пример 1.

Вкладчик открыл в банке счет и положил на него S0
= 150 000 рублей сроком на 4 года под обыкновенные проценты по ставке 18% в год. Какой будет сумма S4
, которую вкладчик получит при закрытии вклада? На сколько рублей вырастет вклад за 4 года? Чему равен коэффициент наращивания?

Решение.

В нашем случае S0
= 150 000, p = 18, n = 4. По формуле Sn
= S0
.
( 1 + n .
p/ 100 рублей имеем S4
=150 000 .
( 1 + 18 .
4 / 100 ) = = 258 000 рублей .

За 4 года вклад возрос на 108 000 рублей = 258 000 рублей – 150 000 рублей. Коэффициент наращивания по формуле Sn
/ S0
=1+n .
p / 100 равен S4
/S0
= 1,72. Он указывает, что за 4 года начальный вклад S0 возрос в 1,72 раза.

Пример 2.

Какую годичную ставку обычных процентов выплачивает года достигнул величины 14 160 рублей ? Обусловьте коэффициент наращивания.

Решение.

По условию, S0
= 12 000, S3
= 14 160, n = 3. Из соотношения Sn
= So
.
( 1 +n .
p / 1 000 ) рублей имеем p = (S3
/ S0
– 1 ) .
1 000 /n. Подставляем в приобретенное выражение данные значения, вычисляем итог: p = 5,(9), т.е. p = 6% . Коэффициент наращивания равен S3
/S0
= 1,18.

2. Сложные проценты.

Если проценты начисляются не только лишь на начальный вклад, да и на приросшие проценты, то такое начисление именуют правилом сложных процентов. Это правило тесновато соединено с формулой определения концентрации раствора опосля n переливаний (формула 2).

Мы говорим, что имеем дело со “сложными процентами”, в том случае, когда некая величина подвержена поэтапному изменению. При всем этом всякий раз ее изменение составляет определенное число процентов от значения, которое эта величина имела на прошлом шаге.

Разглядим поначалу вариант, когда в конце всякого шага величина меняется на одно и то же неизменное количество процентов — р%.

Некая величина S, начальное значение которой равно S0
, в конце первого шага будет равна

S1
=S0
+p/100 х S0
= S0
(1+p/100) .

В конце второго шага ее значение станет равным

S2
=S1
+p/100 х S1
= S1
(1+p/100) = S0
(1+p/100)2
.

тут множитель 1+p/100 указывает, во сколько раз величина S возросла за один шаг. В прошлых задачках о концентрациях эту роль играл множитель

1-a/V0
.

В конце третьего шага

S3
=S2
+p/100 х S2
= S0
(1+p/100)3
,

и т. д.

Несложно осознать, что в конце n-го шага

Формула (4) является начальной формулой при решении почти всех задач на проценты.

Пример3. Сберкасса выплачивает 3% годичных. Во сколько раз возрастет величина вклада через 2 года?

Решение. Пусть величина вклада составляет S0
руб. Тогда через 2 года эта величина станет равной S2
= S0
(1+p/100)2
= (1,03)2
S0
= 1,0609 S0

Ответ. В 1,0609 раза.

Приведем обобщение формулы (4) на вариант, когда прирост величины S на любом шаге собственный.

Пусть величина S в конце первого шага испытывает изменение на p1
%, в конце второго шага — на р2
%, в конце третьего шага — на p3
% и т. д. Если pk
>0, то величина S на этом шаге увеличивается, если pk
<0, то величина S на этом шаге убывает.

Как говорилось выше, изменение величины S на р% равносильно умножению данной величины на множитель 1+p/100. Потому окончательный вид разыскиваемой формулы таковой:

Sn
= S0
(1+p1
/100) (1+p2
/100)… (1+pn
/100) . (формула 5)

тут S0
— первоначальное

время от времени в задачках на составление уравнений встречается понятие “средний процент прироста”. Под сиим термином соображают таковой неизменный процент прироста, который за n шагов давал бы такое же изменение величины S, которое она получает в реальности, при неравных поэтапных процентах конфигурации.

Средний процент прироста q% определяется формулой

S0
(1+p1
/100) (1+p2
/100)… (1+pn
/100) = S0
(1+p/100)n

либо q/100=(1+p1
/100) (1+p2
/100)… (1+pn
/100) -1 .

Отсюда видно, что средний процент прироста неравен среднему арифметическому величин p1
, р2
, …, рn
. тут существует полная работы компании возросла на 4%. На последующий год она возросла на 8%. Найти средний каждогодний прирост продукции за этот период.

Решение. Обозначим средний каждогодний прирост продукции через q%. Тогда

(1+4/100) (1+8/100) = (1+q/100)2
.

Отсюда находим q = — 100 5,98

задачки НА РОСТ ПРОИЗВОДИТЕЛЬНОСТИ

1.Выработка продукции за 1-ый год работы компании возросла на р%, а за последующий год по сопоставлению с начальной она возросла на 10% больше, чем за 1-ый год. Найти, на сколько процентов возросла выработка за 1-ый год, если понятно, что за два года она возросла в общей трудности на 48, 59%?

Решение.

За 1-ый год выработка возросла в (1+р/100) раз по сопоставлению с начальной, за 2-ой год – в (1+(р+10)/100)раз по сопоставлению с началом второго года и в (1+р/100)(1+(р+10)/100) по сопоставлению с начальной и составила 1,4859:

(1+р/100)(1+(р+10)/100) = 1,4859

Отсюда р=17%

2. В течение года завод два раза увеличивал выпуск продукции на одно и то же число процентов. Отыскать это число, если понятно, что сначала года завод каждый месяц выпускал 600 изделий, а в конце года стал выпускать каждый месяц 726 изделий.

Решение.

Пусть х – процент прироста продукции. Тогда опосля первого роста

Выпуск вырастет в (1+х) раз, опосля второго – во столько же. Другими словами

600(1+х)(1+х) = 726

Отсюда х = 10%

3. В оленеводческом совхозе стадо возрастает в итоге естественного прироста и приобретения новейших оленей. Сначала первого года стадо составляло 3000 голов, в конце года совхоз купил 700 голов. В конце второго года стадо составляло 4400 голов. Найти процент естественного прироста.

Решение.

Пусть х – процент естественного прироста. Тогда в конце 1-го года в стаде станет 3000(1+х/100)+700 оленей. За 2-ой год число оленей возрастет в (1+х/100) раз по сопоставлению с началом года и станет 4400.

(3000(1+х/100)+700)(1+х/100) = 4400

Отсюда х=10%

ЗАКЛЮЧЕНИЕ

В реальном реферате рассмотрены способы решения задач, связанных с конфигурацией концентраций, начислением банковских процентов и ростом производительности. Эти задачки решаются по схожим методам. Рассмотрены более обычные задачки, дано их решение.

Не считая того, для сотворения данного реферата на компе был исследован редактор текстов Word. Таковым образом, цель реферата – исследование способов решения задач на концентрации и, банковские проценты и рост производитель-ности – достигнута, задачки, поставленные в реферате, выполнены.

Для решения задач, приведенных в реальном реферате довольно математического аппарата 8 класса. Но, ряд задач по рассмотренным вопросцам можно решить только владея познаниями арифметики, получаемыми в старших классах школы. Потому целенаправлено продолжить тему данного реферата в выпускном классе , тем наиболее, что подобные задачки все почаще встречаются на вступительных экзаменах в ВУЗы.

Перечень литературы

1. М.В. Лурье, Б.И.Александров “Задачки на составление уравнений”.-М.: Наука, 1976.

2. 3000 конкурсных задач по арифметике.-М.: Рольф, Айрис-пресс, 1998.

3. Справочник для поступающих в Столичный институт в 1995г.-М.: Изд-во Моск. Ун-та, 1995.

4. Математика в школе №№ 4,5 1998г.

]]>