Учебная работа. Реферат: Основы графической визуализации вычислений
Индивидуальности графики системы MATLAB
· Построение графика функций одной переменной
· Построение графиков точками и отрезками прямых
· Графики в логарифмическом и полулогарифмическом масштабе
· Гистограммы и диаграммы
· Графики особых типов
· Создание массивов данных для 3d графики
· Построение графиков трехмерных поверхностей, сечений и контуров
· средства управления подсветкой и обзором фигур
· Средства дизайна графиков
· Одновременный вывод нескольких графиков
· Управление цветовой гаммой
· Расцветка трехмерных поверхностей
· Двумерные и трехмерные графические объекты
Главные отличительные черты графики MATLAB
· значительно усовершенствованный интерфейс графических окон;
· введение новейшей панели инструментов Camera для интерактивного конфигурации критерий видимости объекта;
· расширенные способности форматирования графики;
· возможность сотворения графики в отдельных окнах;
· возможность вывода нескольких графических окон;
· возможность перемещения окон по экрану и конфигурации их размеров;
· возможность перемещения области графики снутри графического окна;
· задание разных координатных систем и осей;
· высочайшее свойство графики;
· широкие способности использования цвета;
· легкость установки графических признаков — атрибутов;
· снятие ограничений на число цветов;
· богатство характеристик установок графики;
· возможность получения естественно выглядящих трехмерных фигур и их сочетаний;
· простота построения трехмерных графиков с их проекцией на плоскость;
· возможность построения сечений трехмерных фигур и поверхностей плоскостями;
· многофункциональная разноцветная и полутоновая расцветка;
· возможность имитации световых эффектов при освещении фигур точечным источником света;
· возможность сотворения анимированной графики;
· возможность сотворения объектов для типового интерфейса юзера.
Построение графика функций одной переменной
В режиме конкретных вычислений доступны фактически все способности системы. Обширно употребляется построение графиков разных функций, дающих приятное конфигурации аргумента. При всем этом графики строятся в отдельных масштабируемых и перемещаемых окнах.
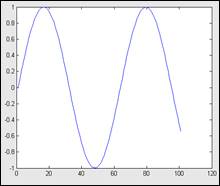
Разглядим простой пример — построение графика синусоиды. MATLAB строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале меж смежными точками. Зададим интервал конфигурации аргумента xот 0 до 10 с шагом 0.1. Для построения графика довольно сначала задать вектор х=0:0.1:10, а потом употреблять команду построения графиков plot (sin(x)).
Вектор xзадает интервал конфигурации независящей переменной от 0 до 10 с шагом 0.1. Функция plotстроит не настоящий график функции sin(x), а только данное числом частей вектора xчисло точек. Эти точки потом просто соединяются отрезками прямых, т. е. осуществляется кусочно-линейная интерполяция данных графика. При 100 точках приобретенная кривая глазом воспринимается как полностью плавная, но при 10 — 20 точках она будет смотреться состоящей из отрезков прямых.
MATLAB строит графики в отдельных окнах, именуемых графическими окнами. В основном меню окна команды пт меню Tools (Инструменты), разрешают вывести либо скрыть инструментальную панель. средства данной нам панели разрешают просто управлять параметрами графиков и наносить на их текстовые комменты в любом месте.
Построение в одном окне графиков нескольких функций
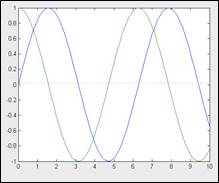
Построим графики сходу 3-х функций:sin(x), cos(x) и sin(x)/х. До этого всего, отметим, что эти функции могут быть обозначены переменными, не имеющими очевидного указания аргумента в виде у (x):
>>y1=sin(x); y2=cos(x); y3=sin(x)/x;
Таковая возможность обоснована тем, что эти переменные являются векторами — как и переменная x. сейчас можно употреблять одну из ряда форм команды
plot: plot(a1, f1, a2, f2, a3, f3,…).
где a1, a2, a3,…- векторы аргументов функций, а f1, f2, f3,… — векторы значений функций, графики которых строятся в одном окне. В нашем случае для построения графиков обозначенных функций мы должны записать последующее:
>> plot (x, y1, x, y2, x, y3)
Можно ждать, что MATLAB в этом случае выстроит, как обычно, точки графиков этих функций и соединит их отрезками линий. Но, если мы выполним эти команды, то никакого графика не получим совершенно. Не исключен даже сбой в работе программки. Причина этого казуса возникнет при вычислении функции y3=sin(x)/x, если x представляет собой массив (вектор), то недозволено употреблять оператор матричного деления /.
Чтоб получить график, нужно вычислять отношение sin(x) к x при помощи оператора поэлементного деления массивов ./
.
>>y1=sin(x); y2=cos(x); y3=sin(x)./x;
Warning: Divide by zero.
(Type «warning off MATLAB:divideByZero» to suppress this warning.)
>> plot(x,y1,x,y2,x,y3)
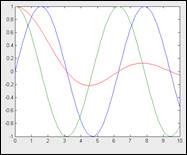
MATLAB выстроил графики всех 3-х функций, но в окне командного режима возникло предупреждение о делении на 0 — в момент, когда х=0. Это гласит о том, что plot «не понимает» о том, что неопределенность sin(x)/x=0/0 устранима и дает 1. Это недочет фактически всех систем для численных вычислений.
Графическая функция
fplot
MATLAB имеет средства для построения графиков и таковых функций, как sin(x)/x, которые имеют устранимые неопределенности. Это делается, при помощи иной графической команды –
fplot: fplot(‘f(x)’, [xmin, xmax])
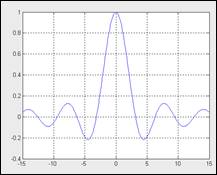
Она дозволяет строить функцию, заданную в символьном виде, в интервале конфигурации аргумента х от xmin до xmax без фиксированного шага конфигурации х. Хотя в процессе вычислений предупреждение о ошибке (деление на 0) выводится, график строится верно, при х=0 sinx/x=1. Команда gridon (сетка)- включает отображение сетки, которая строится пунктирными линиями.
>> fplot(‘sin(x)/x’, [-15,15]); grid on
Построение графиков отрезками прямых
Для отображения функции одной переменной у (x)употребляются графики в декартовой (прямоугольной) системе координат. При всем этом обычно строятся две оси: горизонтальная X и вертикальная Y, и задаются координаты xи у, определяющие узловые точки функции у(x).
Команда plotслужит для построения графиков функций в декартовой системе координат. Эта команда имеет ряд характеристик, рассматриваемых ниже.
· plot (X, Y) — строит график функции у(х),координаты точек (х, у) которой берутся из векторов схожего размера Y и X. Если X либо Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.
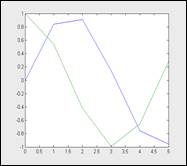
Приведенный ниже пример иллюстрирует построение графиков 2-ух функций — sin(x)и cos(x),значения, функции которых содержатся в матрице Y, а значения аргумента ххранятся в векторе X:
>> x=[0 1 2 3 4 5];
>> y1=sin(x); y2=cos(x);
>> plot(x,y1,x,y2)
На рисунке показан график функций из этого примера. В данном случае ясно видно, что график состоит из отрезков, и если для вас необходимо, чтоб отображаемая функция имела вид гладкой кривой, нужно прирастить количество узловых точек. Размещение их быть может произвольным.
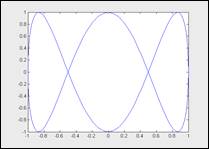
· plot(Y) — строит график у(x),где значения yберутся из вектора Y, а xпредставляет собой индекс соответственного элемента. Если Y содержит всеохватывающие элементы, то строится график plot (real (Y), imag(Y)). Во всех остальных вариантах надуманная часть данных игнорируется.
Пример использования команды plot(Y):
>> x=-2*pi:0.02*pi:2*pi;
>> y=sin(x)+i*cos(3*x);
>> plot(y)
plot(X,Y,S) — подобна командеplot(X,Y), но тип полосы графика можно задавать при помощи строковой константы S.
Значениями константы S могут быть последующие знаки:
цвет полосы
Тип точки
Тип полосы
Желтоватый
y
Точка
.
Сплошная
-
Фиолетовый
m
Окружность
0
Двойной пунктир
;
Голубой
c
Крест
x
Штришок-пунктир
-.
Красноватый
r
Плюс
+
Штриховая
—
Зеленоватый
g
Звездочка
*
Голубий
b
Квадрат
s
Белоснежный
w
Ромб
d
Темный
k
Треугольник (вниз)
v
Треугольник (ввысь)
^
Треугольник (на лево)
<
Треугольник (на Право)
>
Пятиугольник
p
Шестиугольник
h
Таковым образом, при помощи строковой константы S можно изменять цвет полосы, представлять узловые точки разными отметками (точка, окружность, крест, треугольник с разной ориентацией верхушки и т. д.) и поменять тип полосы графика.
· рlot (X1,Y1, S1, Х2, Y2, S2, ХЗ, Y3, S3,…) — эта команда строит на одном графике ряд линий, представленных данными вида (X.,Y.,S.), где X. иY. — векторы либо матрицы, а S. — строчки. При помощи таковой конструкции может быть построение, к примеру, графика функции линией, цвет которой различается от цвета узловых точек. Так, если нужно выстроить график функции линией голубого цвета с красноватыми точками, то сначала нужно задать построение графика с точками красноватого цвета (без полосы), а потом графика лишь полосы голубого цвета (без точек).
При отсутствии указания на цвет линий и точек он выбирается автоматом из таблицы цветов (белоснежный исключается). Если линий больше 6, то выбор цветов повторяется. Для монохромных систем полосы выделяются стилем.
Разглядим пример построения графиков 3-х функций с разным стилем представления каждой из их:
>> x=-2*pi:0.1*pi:2*pi;
>> y1=sin(x);y2=sin(x).^2;
>> y2=sin(x).^2;
>> y3=sin(x).^3;
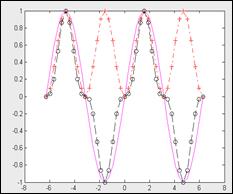
>>plot(x,y1,’-m’,x,y2,’-.+r’,x,y3,’—ok’)
тут график функции y1 строится сплошной фиолетовой линией, график у2 строится штришок пунктирной линией с точками в виде знака «плюс» красноватого цвета, а график yЗ строится штриховой линией с кружками темного цвета.
Графики в логарифмическом масштабе
Для построения графиков функций со значениямиxи у, изменяющимися в широких границах, часто употребляются логарифмические масштабы. Разглядим команды, которые употребляются в таковых вариантах.
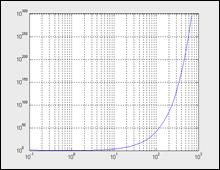
· loglogx(…) — синтаксис команды аналогичен ранее рассмотренному для функции plot(…). Логарифмический масштаб употребляется для координатных осей Xи Y. Ниже дан пример внедрения данной команды:
>> x=logspace(-1,3);
>> loglog(x,exp(x)./x) grid on
Функция x = logspace(d1, d2) сформировывает вектор-строку, содержащую 50 равноотстоящих в логарифмическом масштабе точек, которые покрывают спектр от 10d1
до 10d2
.
Функция x =logspace(d1, d2, n) сформировывает вектор-строку, содержащую n равноотстоящих в логарифмическом масштабе точек, которые покрывают спектр от 10d1
до 10d2
.
На рисунке представлен график функции ехр(х)/хв логарифмическом масштабе. Командой gridon строится координатная сетка. Неравномерное размещение линий координатной сетки показывает на логарифмический масштаб осей.
Графики в полулогарифмическом масштабе
В неких вариантах предпочтителен полулогарифмический масштаб графиков, когда по одной оси задается логарифмический масштаб, а по иной — линейный.
Для построения графиков функций в полулогарифмическом масштабе употребляются последующие команды: semilogx(…) — строит график функции в логарифмическом масштабе (основание 10) по оси X и линейном по оси Y; semilogy(…)— строит график функции в логарифмическом масштабе по оси Y и линейном по оси X.
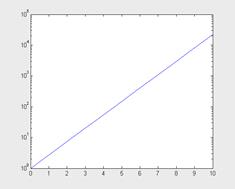
Запись характеристик (…) производится по аналогии с функцией plot(…). приведем пример построения графика экспоненциальной функции:
>> x=0:0.5:10;
>> semilogy(x,exp(x))
Несложно увидеть, что при таком масштабе график экспоненциальной функции выродился в прямую линию. Масштабной сетки сейчас уже нет.
Столбцовые диаграммы
Столбцовые диаграммы обширно употребляются в литературе, посвященной финансам и экономике, также в математической литературе. Ниже представлены команды для построения таковых диаграмм.
· bar(x, Y) — строит столбцовый график частей вектора Y(либо группы столбцов для матрицы Y) со спецификацией положения столбцов, данной значениями частей вектора х, которые должны идти в однообразно вырастающем порядке;
· bar(Y)— строит график значений частей матрицы Yтак же, как обозначено выше, но практически для построения графика употребляется вектор х=1:m;
· bar(x,Y,WIDTH) илиbar(Y,WIDTH) — команда подобна ранее рассмотренным, но со спецификацией ширины столбцов (при WIDTH > 1 столбцы в одной и той же позиции перекрываются). По дефлоту задано WIDTH = 0.8.
Может быть применение этих установок и в последующем виде: bar(…. ‘Спецификация’) для задания спецификации графиков, к примеру типа линий, цвета и т. д., по аналогии с командой plot. Спецификация ‘stacked’ задает рисование всех n столбцов в позиции m друг на друге.
Пример построения столбцовой диаграммы матрицы размером 12×3 приводится ниже:
>> %Столбцовая диаграмма
>> subplot(2,1,1), bar(rand(12,3),stacked’), colormap(cool)

Кроме команды bar(…) существует подобная ей по синтаксису команда barh(…), которая» строит столбцовые диаграммы с горизонтальным расположением столбцов.
>> subplot(2,1,1), barh(rand(5,3), ‘stacked’),colormap(cool)
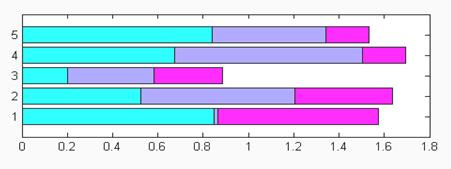
Какое конкретно размещение столбцов избрать, зависит от юзера, использующего эти команды для представления собственных данных.
Построение гистограмм
Традиционная гистограмма охарактеризовывает числа попаданий значений частей вектора Y в М интервалов с представлением этих чисел в виде столбцовой диаграммы. Для получения данных для гистограммы служит функция hist, записываемая в последующем виде:
· N=hist(Y) — возвращает вектор чисел попаданий для 10 интервалов, избираемых автоматом. Если Y — матрица, то выдается массив данных о числе попаданий для всякого из ее столбцов;
· N=hist(Y,M) — подобна вышерассмотренной, но употребляется М интервалов (М- скаляр);
· N=hist(Y,X) — возвращает числа попаданий частей вектора Y в интервалы, центры которых заданы элементами вектора X;
· [N,X]=HIST(…) — возвращает числа попаданий в интервалы и данные о центрах интервалов.
Команда hist(…) с синтаксисом, аналогичным приведенному выше, строит график гистограммы. В последующем примере строится гистограмма для 1000 случайных чисел и выводится вектор с данными о числах их попаданий в интервалы, данные вектором x:
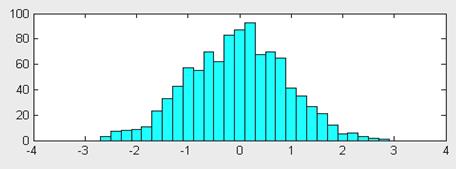
>> x=-3:0.2:3;
>> y=randn(1000,1);
>> hist(y,x)
>> h=hist(y,x)
h =
Columns 1 through 9
0 0 3 7 8 9 11 23 33
Columns 10 through 18
43 57 55 70 62 83 87 93 68
Columns 19 through 27
70 65 41 35 27 21 12 5 6
Columns 28 through 31
3 2 1 0
Несложно увидеть, что распределение случайных чисел близко к нормальному закону. Увеличив их количество, можно следить еще большее соответствие этому закону.
Создание массивов данных для 3d графики
Трехмерные поверхности обычно описываются функцией 2-ух переменных z(x,y). Специфичность построения трехмерных графиков просит не попросту задания ряда значений xи у, другими словами векторов x и у. Она просит определения для X и Y двумерных массивов — матриц. Для сотворения таковых массивов служит функция meshgrid. В главном она употребляется вместе с функциями построения графиков трехмерных поверхностей. Функция meshgrid записывается в последующих формах:
· [X,Y] = meshgrid(x) — подобна [X,Y] = meshgrid(x, x);
· [X,Y,Z] = meshgrid(x, y, z) — возвращает трехмерные массивы, применяемые для вычисления функций 3-х переменных и построения трехмерных графиков;
· [X,Y] = meshgrid(x,y) — конвертирует область, заданную векторами x и у, в массивы X и Y, которые могут быть применены для вычисления функции 2-ух переменных и построения трехмерных графиков. Строчки выходного массива X являются копиями вектора x; а столбцы Y — копиями вектора у.
Пример:
>> [X,Y]=meshgrid(1:4, 13:17)
X =
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
Y =
13 13 13 13
14 14 14 14
15 15 15 15
16 16 16 16
17 17 17 17
Приведем еще один пример внедрения функции meshgrid:
>> [X,Y]=meshgrid(-2:0.2:2, -2:0.2:2);
Таковой вызов функции дозволяет задать опорную плоскость для построения трехмерной поверхности при изменении x и y от-2 до 2с шагом 0.2.
Функция ndgridявляется многомерным аналогом функции meshgrid:
· [Х1,Х2,ХЗ,…] = ndgrid(x1,x2,x3….) — конвертирует область, заданную векторами x1,.x,x3…, в массивы Х1,Х2,ХЗ…, которые могут быть применены для вычисления функций нескольких переменных и многомерной интерполяции, i-я размерность выходного массива Xi является копией вектора xi;
[XI,Х2….] = ndgrid(x) — подобна [XI,Х2….] = ndgrid(x,x,…).
Пример внедрения функции ndgridпредставлен ниже:
>> [X1,X2]=ndgrid(-2:0.2:2,-2:0.2:2);
>> Z=X1.*exp(-X1.^2-X2.^2);
>> mesh(Z)
Построение графиков поверхностей
Команда plot3(…) является аналогом команды plot(…), но относится к функции 2-ух переменных z(x, у). Она строит аксонометрическое изображение трехмерных поверхностей и представлена последующими формами:
· plot3(x, y, z) — строит массив точек, представленных векторами x, у и z соединяя их отрезками прямых. Эта команда имеет ограниченное применение;
· plot3(X,Y,Z), где X, Y и Z— три матрицы схожего размера, строит точки с координатами X(i,:),Y(i,:) и Z(i,:) и соединяет их отрезками прямых.
Ниже дан пример построения трехмерной поверхности, описываемой функцией
z(х,у)=х^2+у^2;
>> [X,Y]=meshgrid(-3:0.15:3);
>> Z=X.^2+Y.^2;
>> plot3(X,Y,Z)
График данной нам поверхности показан на рисунке:
· plot3 (X, Y, Z, S) — обеспечивает построения, подобные рассмотренным ранее, но со спецификацией стиля линий и точек, соответственной спецификации команды plot. Ниже дан пример внедрения данной нам команды для построения поверхности кружками:
>> [X,Y]=meshgrid(-3:0.15:3);
>> Z=X.^2+Y.^2;
>> plot3(X,Y,Z,’o’)
График поверхности, построенный кружками, показан на рисунке:

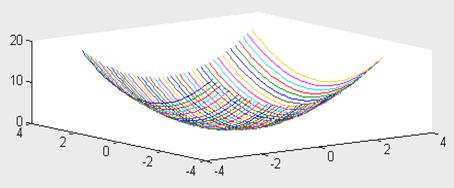
· plot3(x1 ,y1,z1, s1,х2,у2,z2, s2,х3,уЗ,z3,s3,…)—
строит на одном рисунке графики нескольких функций z1(x1 ,y1),z2(x2,y2) и т. д. со спецификацией линий и маркеров каждой из их.
Пример внедрения крайней команды дан ниже:
>> [X,Y]=meshgrid(-3:0.15:3);
>> Z=X.^2+Y.^2;
>> plot3(X,Y,Z,’-k’,Y,X,Z,’k’)
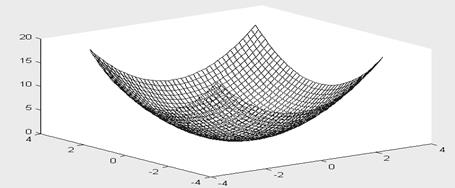
В данном случае строятся два графика одной и той же функции с взаимно перпендикулярными образующими линиями. Потому график имеет вид сетки без расцветки ее ячеек (припоминает проволочный основа фигуры).
установка титульной надписи
Опосля того как график уже построен, MATLAB дозволяет выполнить его форматирование либо оформление в подходящем виде. Надлежащие этому средства описаны ниже. Так, для установки над графиком титульной надписи употребляется последующая команда:
· title( ‘string’) — установка на двумерных и трехмерных графиках титульной надписи, данной строковой константой ‘string’.
установка осевых надписей
Для установки надписей около осей х, уи z употребляются последующие команды:
xlabel(‘String’)
ylabel (‘String’)
zlabell (‘String’)
Соответственная надпись задается символьной константой либо переменной ‘String’. Пример установки титульной надписи и надписей по осям графиков приводится ниже:
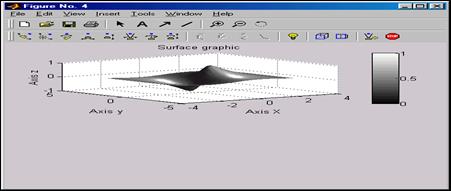
>> surfl(X,Y,Z)
>> [X,Y]=meshgrid(-3:0.15:3);
>> Z=sin(X)./(X.^2+Y.^2+0.3);
>> surfl(X,Y,Z)
>> colorbar
>> colormap(gray)
>> shading interp
>> xlabel(‘Axis X’)
>> ylabel(‘Axis Y’)
>> zlabel(‘Axis Z’)
>> title(‘Surfacegraphic’)
Ввод текста в хоть какое пространство графика
Нередко возникает необходимость прибавления текста в определенное пространство графика, к примеру для обозначения той либо другой кривой графика. Для этого употребляется команда text:
· text(X,Y, ‘string’) — добавляет в двумерный график текст, данный строковой константой ‘string’, так что начало текста размещено в точке с координатами (X, Y).Если X и Y заданы как одномерные массивы, то надпись помещается во все позиции [x(i) ,y(i)];
· text(X,Y,Z. ‘string’) — добавляет в трехмерный график текст, данный строковой константой ‘string’, так что начало текста размещено в позиции, данной координатами X, Y и Z.
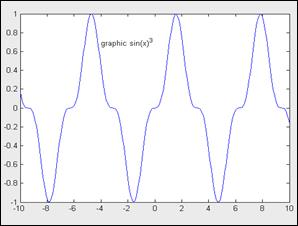
В приведенном примере надпись располагается под кривой графика в позиции (-4, 0.7):
>> x=-10:0.1:10;
>> plot(x,sin(x).^3)
>> text(-4,0.7,’graphic sin(x)^3′)
Размещение текста при помощи мыши
Весьма удачный метод ввода текста предоставляет команда gtext:
· gtext(‘string’) — задает выводимый на график текст в виде строковой константы ‘ string’ и выводит на график, перемещаемый мышью маркер в виде крестика. Установив маркер в необходимое пространство, довольно щелкнуть хоть какой клавишей мыши для вывода текста;
· gtext (С) — дозволяет аналогичным образом расположить многострочную надпись из массива строковых переменных С.
Пример внедрения команды gtext:
>> x=-10:0.1:10;
>> plot(x,sin(x).^3)
>> gtext(‘Function sin(x)^3’)
Установив перекрестие в необходимое пространство графика, довольно надавить всякую кнопку либо всякую клавишу мыши, и на этом месте покажется надпись
Вывод пояснений
Пояснение в виде отрезков линий со справочными надписями, размещаемое снутри графика либо около него, именуется легендой. Для сотворения легенды употребляются разные варианты команды legend:
· legend(string1,,string2, string3,…) — добавляет к текущему графику легенду в виде строк, обозначенных в перечне характеристик;
· legend (М) — располагает легенду, используя данные из строковой матрицы М;
· legend OFF — избавляет ранее выведенную легенду;
· legend (….Pos) — помещает легенду в буквально определенное пространство, специфицированное параметром Pos:
— Pos=0 — наилучшее пространство, выбираемое автоматом;
— Pos=1- верхний правый угол;
— Pos=2 — верхний левый угол;
— Pos=3 — нижний левый угол;
— Pos=4 — нижний правый угол;
— Pos=-1- справа от графика.
Чтоб перенести легенду, установите на нее курсор, нажмите левую клавишу мыши и перетащите легенду в нужную позицию.
Команда legend может употребляться с двумерной и трехмерной графикой и со специальной графикой — столбцовыми и радиальными диаграммами и т. д. Двойным щелчком можно вывести легенду на редактирование.

Пример, приведенный ниже, строит график 3-х функций с легендой, размещенной в поле графика:
>> x=-2*pi:0.1*pi:2*pi;
>> y1=sin(x);
>> y2=sin(x).^2;
>> y3=sin(x).^3;
>> plot(x,y1,’-m’,x,y2,’-.+r’,x,y3,’—ok’)
>> legend(‘Function 1′,’Function 2’, ‘Function 3’);
Управление качествами осей графиков
Обычно графики выводятся в режиме автоматического масштабирования. Последующие команды класса axis меняют эту ситуацию:
· axis([XMIN XMAX YMIN YMAX]) — установка диапазонов координат по осям xи у для текущего двумерного графика;
· axis([XMIN XMAX YMIN YMAX ZMIN ZMAX]) — установка диапазонов координат по осям x, у и zтекущего трехмерного графика;
· axis auto — установка характеристик осей по дефлоту;
· axis Manual — «замораживает» масштабирование в текущем состоянии, чтоб при использовании команды hold on последующие графики употребляли те же характеристики осей;
· axis tight — устанавливает спектры координат по осям в согласовании с спектрами конфигурации данных;
· axis ij — задает «матричную» прямоугольную систему координат с началом координат в левом верхнем углу, ось i — вертикальная, размечаемая сверху вниз, ось j — горизонтальная и размечается слева вправо;
· axis xy — устанавливает декартову систему координат с горизонтальной осью х, размечаемой слева вправо, и вертикальной осью у, размечаемой снизу ввысь. Начало координат располагается в нижнем левом углу;
· axis equal — включает масштаб с схожим расстоянием меж метками по осям х, уи z;
· axis image — устанавливает масштаб, при котором пиксели изображения стают квадратами;
· axis square — устанавливает текущие оси в виде квадрата (либо куба в трехмерном случае) с схожим расстоянием меж метками и схожей длиной осей;
· axis normal — восстанавливает масштаб, отменяя установки axis equal и axissquare;
· axis vis3d — «замораживает» пропорции осей для способности поворота трехмерных объектов;
· axis off — убирает с осей их обозначения и маркеры; 0
· axis on — восстанавливает ранее введенные обозначения осей и маркеры;
· V=axis — возвращает вектор- строчку, содержащую коэффициенты масштабирования для текущего графика. Если текущий график двумерный, то вектор имеет 4 компонента, если трехмерный — 6 компонент.
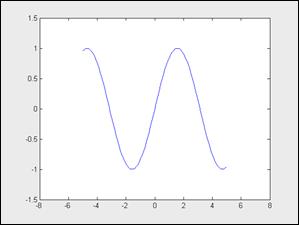
Последующий пример иллюстрирует применение команды axis при построении двумерного графика функции одной переменной:
>> axis([-10 10 -1.5 1.5])
>> x=-5:0.1:5;
>> plot(x, sin(x));
>> axis([-8 8 -1.5 1.5])
Обратите внимание, что сейчас масштабы осей заданы командой axis, а не спектром конфигурации значений xи у.
Включение и выключение сетки
В математической, физической и другой литературе при построении графиков в дополнение к разметке осей нередко употребляют масштабную сетку. Команды grid разрешают задавать построение сетки либо отменять это построение:
· grid on — добавляет сетку к текущему графику;
· grid off — отключает сетку;
· grid — поочередно производит включение и отключение сетки.
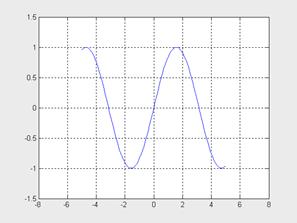
Команды grid устанавливают характеристики объектов XGrid, Ygrid и Zgrid для текущих осей. Ниже приведен пример из предыдущего раздела с добавлением в него команды grid:
>> x=-5:0.1:5;
>> plot(x, sin(x));
>> axis([-8 8 -1.5 1.5])
>> gridon
Наложение графиков друг на друга
В почти всех вариантах лучше построение почти всех наложенных друг на друга графиков в одном и том же окне. Для этого служит команда продолжения графических построений hold. Она употребляется в последующих формах:
· hold on — обеспечивает продолжение вывода графиков в текущее окно, что дозволяет добавлять следующие графики к уже имеющимся;
· hold off — отменяет режим продолжения графических построений;
· hold— работает как переключатель, поочередно включая режим продолжения графических построений и отменяя его.
Команда hold on устанавливает
Графики синусоиды и 3-х параметрических функций в одном окне

Приведенный ниже пример указывает, как при помощи команды hold on на график синусоиды накладываются еще три графика параметрически данных функций:
>> x=-5:0.1:5;
>> plot(x, sin(x));
>> hold on
>> plot(sin(x), cos(x));
>> plot(2*sin(x), cos(x));
>> plot(4*sin(x), cos(x));
>> holdoff
В конце приведенного фрагмента программки команда holdoff отключает режим прибавления графиков к ранее построенным графикам.
Разбиение графического окна
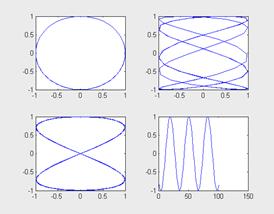
Бывает, что в одном окне нужно расположить несколько координатных осей с разными графиками без наложения их друг на друга. Для этого употребляются команды subplot, используемые перед построением графиков:
· subplot — делает новейшие объекты класса axes (подокна);
· subplot(m,n, p) либо subplot(mnp) — разбивает графическое окно на тхп подокон, при всем этом m — число подокон по горизонтали, n — число подокон по вертикали, а p— номер подокна, в которое будет выводиться текущий график (подокна отсчитываются поочередно по строчкам);
· subplot(H), где Н — дескриптор для объекта axes, дает другой метод задания подокна для текущего графика;
· subplot( ‘position’,[left bottom width height]) — делает подокно с данными нормализованными координатами (в границах от 0.0 до 1.0);
· subplot(lll) и clf reset — убирают все подокна и возвращают графическое окно в обыденное состояние.
Последующий пример иллюстрирует применение команды subplot:
>> x=-5:0.1:5;
>> subplot(2,2,1), plot(sin(x), cos(x))
>> subplot(2,2,2), plot(sin(5*x), cos(2*x+0.2))
>> subplot(2,2,3), plot(sin(4*x), cos(2*x))
>> subplot(2,2,4), plot(cos(2*x))
В этом примере поочередно строятся четыре графика различного типа, размещаемых в различных подокнах.
Для всех графиков вероятна персональная установка доп объектов, к примеру титульных надписей, надписей по осям и т. д.
Изменение масштаба графика
Для конфигурации масштаба двумерных графиков употребляются команды класса zoom:
· zoom— переключает состояние режима интерактивного конфигурации масштаба для текущего графика;
· zoom (FACTOR) устанавливает масштаб в согласовании с коэффициентом FACTOR;
· zoom on — включает режим интерактивного конфигурации масштаба для текущего графика;
· zoom off — выключает режим интерактивного конфигурации масштаба для текущего графика;
· zoom out — обеспечивает полный просмотр, т. е. устанавливает обычный масштаб графика;
· zoom xon либо
zoom yon — включает режим конфигурации масштаба лишь по оси xили по оси у;
· zoom reset — запоминает текущий масштаб в качестве масштаба по дефлоту для данного графика;
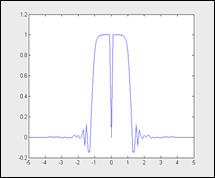
Команда zoom дозволяет управлять масштабированием графика при помощи мыши. Для этого нужно подвести курсор мыши к интересующей вас области рисунка. Если команда zoom включена (on), то нажатие левой клавиши наращивает масштаб в два раза, а правой — уменьшает в два раза. При нажатой левой кнопочке мыши можно выделить пунктирным черным прямоугольником подходящий участок графика — при отпускании клавиши он покажется в увеличенном виде и в том масштабе, который соответствует выделяющему прямоугольнику.
Разглядим работу команды zoom на последующем примере:
>> x=-5:0.1:5;
>> plot(x, sin(x.^5)./(x.^5+eps))
>> zoomon
Опосля прекращения манипуляций левой клавишей мыши график воспримет вид, показанный на рисунке. сейчас в полный размер графического окна будет развернуто изображение, попавшее в выделяющий прямоугольник.

Команда zoom, таковым образом, делает функцию «лупы», позволяющей следить в увеличенном виде отдельные фрагменты сложных графиков. Но следует учесть, что для наблюдения фрагментов графиков при высочайшем увеличении они должны быть заданы огромным количеством точек. По другому вид отдельных фрагментов и тем наиболее особенных точек (в нашем случае это точка при xвблизи нуля) будет значительно различаться от настоящего.
установка цветовой палитры
Так как графика MATLAB обеспечивает получение цветных изображений, в ней есть ряд установок для управления цветом и разными световыми эффектами. Посреди их принципиальное пространство занимает установка цветовой палитры. Гамма цветов RGB задается матрицей MAP из 3-х столбцов, определяющих значения интенсивности красноватого (red), зеленоватого (green) и голубого (blue) цветов. Их интенсивность задается в относительных единицах от 0.0 до 1.0. к примеру, [0 0 0] задает темный цвет, [1 1 1] — белоснежный цвет, [0 0 1] — голубий цвет. При изменении интенсивности цветов в обозначенных границах может быть задание хоть какого цвета. Таковым образом, цвет соответствует принятому формату RGB.
Для установки цветовой палитры служит команда colormap, записываемая в последующих формах:
· colormap( ‘default’) — устанавливает гамму по дефлоту, при которой распределение цветов соответствует радуге;
· colormap(MAP) — устанавливает гамму RGB, заданную матрицей MAP;
· C= colormap — функция возвращает матрицу текущей цветовой палитры С.
m-файл с именованием colormap устанавливает характеристики цветов для текущего графика.
Команда help graph3d вместе с иным выводит полный перечень соответствующих палитр, применяемых графической системой MATLAB:
· hsv- цвета радуги;
· hot — чередование темного, красноватого, желтоватого и белоснежного цветов;
· gray — линейная гамма в колерах сероватого цвета;
· bone — сероватые цвета с цветом голубого;
· copper — линейная гамма с цветами меди;
· pink — розовые цвета с цветами пастели;
· white- гамма белоснежного цвета;
· flag — чередование красноватого, белоснежного, голубого и темного цветов;
· lines — гамма с чередованием цветов линий;
· colorcube- расширенная гамма RGB;
· jet- разновидность палитры HSV;
· prism- призматическая гамма цветов;
· cool — цвета голубого и фиолетового цветов;
· autumn -оттенки красноватого и желтоватого цветов;
· spring — цвета желтоватого и фиолетового цветов;
· winter — цвета голубого и зеленоватого цветов;
· summer — цвета зеленоватого и желтоватого цветов.
Все эти палитры могут служить параметрами команды colormap, к примеру colormap(hsv) практически устанавливает то же, что и команда colormap( ‘default’).
Построение сферы
Для расчета массивов X, Y и Z координат точек сферы как трехмерной фигуры употребляется функция sphere:
· [X,Y,Z]=sphere(N) — генерирует матрицы X, Y и Z размера (N+1)x (N+1) для следующего построения сферы при помощи установок surfl (X, Y,Z) либо surfl(X,Y,,Z);
· [X,Y,Z]=sphere — подобна предыдущей функции при N=20.
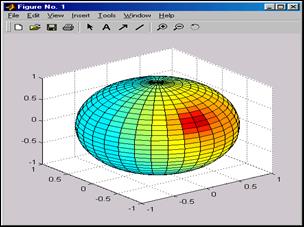
Пример внедрения данной нам функции:
>> [X,Y,Z]=sphere(30);
>> surfl(X,Y,Z)
Отлично видны геометрические преломления (сфера приплюснута), связанные с различными масштабами по координатным осям.
Обратите внимание на то, что конкретно многофункциональная расцветка сферы присваивает ей достаточно близкий к реальности вид. В данном случае цвет задается вектором Z.
]]>

