Учебная работа. Реферат: Теория игр и принятие решений
а) в критериях риска;
б) в критериях неопределённости;
в) в критериях конфликта либо противодействия (активного противника).
Теория полезности и принятия решений.
Принятие решений в критериях риска.
Аспект ожидаемого значения.
Внедрение аспекта ожидаемого значения обосновано рвением максимизировать ожидаемую Прибыль (либо минимизировать ожидаемые издержки). Внедрение ожидаемых величин подразумевает возможность неоднократного решения одной и той же задачки, пока не будут получены довольно четкие расчётные формулы. Математически это смотрится так: пусть Х– случайная величина с математическим ожиданием MX и дисперсией DX. Если x1
,x2
,…,xn
– значения случайной величины (с.в.) X, то среднее арифметическое их (выборочное среднее) значений 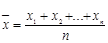 имеет дисперсию
имеет дисперсию 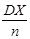 . Таковым образом, когда n®¥
. Таковым образом, когда n®¥
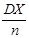 ® 0 и
® 0 и 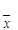 ®MX.
®MX.
Иными словами при довольно большенном объёме подборки разница меж средним арифметическим и математическим ожиданием стремится к нулю (так именуемая предельная аксиома теории вероятности). Как следует, внедрение аспекта ожидаемое
Пример 1. Требуется принять решение о том, когда нужно проводить профилактический ремонт ПЭВМ, чтоб минимизировать утраты из-за неисправности. В случае если ремонт будет делается очень нередко, Издержки на сервис будут большенными при малых потерях из-за случайных поломок.
Потому что нереально предсказать заблаговременно, когда возникнет неисправность, нужно отыскать возможность того, что ПЭВМ выйдет из строя в период времени t. В этом и состоит элемент ”риска”.
Математически это смотрится так: ПЭВМ ремонтируется персонально, если она тормознула из-за поломки. Через T интервалов времени производится профилактический ремонт всех n ПЭВМ. нужно найти наилучшее один интервал времени.
Пусть рt
– возможность выхода из строя одной ПЭВМ в момент t, а nt
– случайная величина, равная числу всех вышедших из строя ПЭВМ в этот же момент. Пусть дальше С1
– издержки на ремонт неисправной ПЭВМ и С2
– Издержки на профилактический ремонт одной машинки.
Применение аспекта ожидаемого значения в данном случае оправдано, если ПЭВМ работают в течение огромного периода времени. При всем этом ожидаемые издержки на один интервал составят
ОЗ = 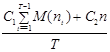 ,
,
где M(nt
) – математическое ожидание числа вышедших из строя ПЭВМ в момент t. Потому что nt
имеет биномиальное распределение с параметрами (n, pt
), то M(nt
) = npt
. Таковым образом
ОЗ = 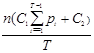
Нужные условия оптимальности T*
имеют вид:
ОЗ (T*
-1) ³ ОЗ (T*
),
ОЗ (T*
+1) ³ ОЗ (T*
).
Как следует, начиная с малого значения T, вычисляют ОЗ(T), пока не будут удовлетворены нужные условия оптимальности.
Пусть С1
= 100; С2
= 10; n = 50. значения pt
имеют вид:
T
рt
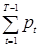
ОЗ(Т)
1
0.05
0
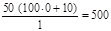
2
0.07
0.05
375
3
0.10
0.12
366.7
4
0.13
0.22
400
5
0.18
0.35
450
T*
® 3 , ОЗ(Т*
) ® 366.7
Как следует профилактический ремонт нужно созодать через T*
=3 интервала времени.
Аспект “ожидаемое
Аспект ожидаемого значения можно видоизменять так, что его можно будет применить и для изредка циклических ситуаций .
Если х – с. в. с дисперсией DX, то среднее арифметическое 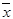 имеет дисперсию
имеет дисперсию 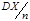 , где n– число слогаемых в
, где n– число слогаемых в 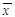 . Как следует, если DX миниатюризируется, и возможность того, что
. Как следует, если DX миниатюризируется, и возможность того, что 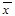 близко к MX, возрастает. Как следует, целенаправлено ввести аспект, в каком максимизация ожидаемого значения прибыли смешивается с минимизацией её дисперсии.
близко к MX, возрастает. Как следует, целенаправлено ввести аспект, в каком максимизация ожидаемого значения прибыли смешивается с минимизацией её дисперсии.
Пример 2. Применим аспект “ожидаемое один интервал времени, т.е. дисперсию
зТ
=
Т.к. nt
, t =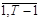 – с.в., то зТ
– с.в., то зТ
также с.в. С.в. nt
имеет биномиальное распределение с M(nt
) = npt
и D(nt
) = npt
(1–pt
). Как следует,
D(зТ
) = D(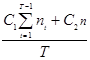 ) =
) =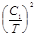 D(
D(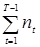 ) =
) =
= 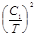
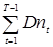 =
= 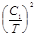
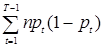 = n
= n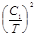 {
{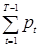 –
–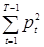 },
},
где С2
n = const.
Из примера 1 следует, что
М(зТ
) = М(з(Т)).
Как следует разыскиваемым аспектом будет минимум выражения
М(з(Т)) + к D(зТ
).
Замечание. Константу “к” можно разглядывать как уровень не склонности к риску, т.к. “к” описывает “степень способности” дисперсии Д(зТ
) по отношению к математическому ожиданию. к примеру, если бизнесмен, в особенности остро реагирует на огромные отрицательные отличия прибыли вниз от М(з(Т)), то он может избрать “к” много больше 1. Это придаёт больший вес дисперсии и приводит к решению, уменьшающему возможность огромных утрат прибыли.
При к =1 получаем задачку
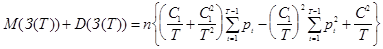

По данным из примера 1 можно составить последующую таблицу
Т
pt
pt
2
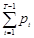
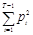
М(з(Т))+D(з(Т))
1
0.05
0.0025
0
0
500.00
2
0.07
0.0049
0.05
0.0025
6312.50
3
0.10
0.0100
0.12
0.0074
6622.22
4
0.13
0.0169
0.22
0.0174
6731.25
5
0.18
0.0324
0.35
0.0343
6764.00
Из таблицы видно, что профилактический ремонт нужно созодать в течение всякого интервала Т*
=1.
Аспект предельного уровня.
Аспект предельного уровня не дает рационального решения, максимизирующего, к примеру, Прибыль либо минимизирующего издержки. Быстрее он соответствует определению применимого метода действий.
Пример 3. Представим, что величина спроса x в единицу времени (интенсивность спроса) на некий продукт задаётся непрерывной функцией распределения f(x). Если припасы в исходный момент невелики, в предстоящем вероятен недостаток продукта. В неприятном случае к концу рассматриваемого периода припасы нереализованного продукта могут оказаться весьма большенными. В обоих вариантах вероятны утраты.
Т.к. найти утраты от недостатка весьма тяжело, ЛПР может установить нужный уровень припасов таковым образом, чтоб величина ожидаемого недостатка не превосходила А1
единиц, а величина ожидаемых излишков не превосходила А2
единиц. Другими словами, пусть I– разыскиваемый уровень припасов. Тогда
ожидаемый недостаток = 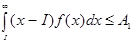 ,
,
ожидаемые избытки =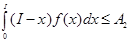 .
.
При случайном выборе А1
и А2
обозначенные условия могут оказаться противоречивыми. В этом случае нужно ослабить одно из ограничений, чтоб обеспечить допустимость.
Пусть, к примеру,
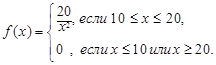

Тогда
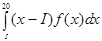 =
=  = 20(ln
= 20(ln +
+ – 1)
– 1)
 =
=  = 20(ln
= 20(ln +
+ – 1)
– 1)
Применение аспекта предельного уровня приводит к неравенствам
ln I –  ³ ln 20 –
³ ln 20 –  – 1 = 1.996 –
– 1 = 1.996 –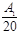
ln I –  ³ ln 10 –
³ ln 10 –  – 1 = 1.302 –
– 1 = 1.302 –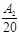
Предельные значения А1
и А2
должны быть выбраны так, что бы оба неравенства производились хотя бы для 1-го значения I.
К примеру, если А1
= 2 и А2
= 4, неравенства принимают вид
ln I – 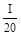 ³ 1.896
³ 1.896
ln I – 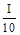 ³ 1.102
³ 1.102
Спрос. Из таблицы видно, что оба условия производятся для I, из интервала (13,17)
I
10
11
12
13
14
15
16
17
18
19
20
ln I – 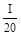
1.8
1.84
1.88
1.91
1.94
1.96
1.97
1.98
1.99
1.99
1.99
lnI–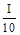
1.3
1.29
1.28
1.26
1.24
1.21
1.17
1.13
1.09
1.04
0.99
Хоть какое из этих значений удовлетворяет условиям задачки.
Принятие решений в критериях неопределённости.
Будем полагать, что лицу, принимающему решение не противоборствует разумный противник.
Данные, нужно для принятия решения в условии неопределенности, обычно задаются в форме матрицы, строчки которой соответствуют вероятным действиям, а столбцы – вероятным состояниям системы.
Пусть, к примеру, из некого материала требуется сделать изделие, долговечность которого при допустимых издержек нереально найти. Перегрузки числятся известными. Требуется решить, какие размеры обязано иметь изделие из данного материала.
Варианты решения таковы:
Е1
– выбор размеров из суждений наибольшей долговечности ;
Еm
– выбор размеров из суждений малой долговечности ;
Ei
– промежные решения.
Условия требующие рассмотрения таковы :
F1
– условия, обеспечивающие наибольшей долговечность;
Fn
–условия, обеспечивающие min долговечность;
Fi
– промежные условия.
Под результатом решения eij
= е(Ei
; Fj
) тут можно осознавать оценку, подобающую варианту Ei
и условиям Fj
и характеризующие Прибыль, полезность либо надёжность. Обычно мы будем именовать таковой итог пользой решения.
Тогда семейство (матрица) решений имеет вид :
имеет вид :
F1
F2
. . .
Fn
E1
e11
e12
. . .
e1n
E2
e21
e22
. . .
e2n
. . .
. . . . . . . . . . . . . . . .
Em
em1
em2
. . .
emn
Чтоб придти к конкретному и по способности наивыгоднейшему варианту решению нужно ввести оценочную (мотивированную) функцию. При всем этом матрица решений  сводится к одному столбцу. Любому варианту Ei
сводится к одному столбцу. Любому варианту Ei
приписывается, т.о., некий итог eir
, характеризующий, в целом, все последствия этого решения. Таковой итог мы будем в предстоящем обозначать этим же эмблемой eir
.
Традиционные аспекты принятия решений .
1. Минимаксный аспект .
правило выбора решения в согласовании с минимаксным аспектом (ММ-критерием) можно интерпретировать последующим образом:
матрица решений дополняется ещё одним столбцом из меньших результатов eir
каждой строчки. нужно избрать те варианты в строчках которых стоят наибольшее
Избранные т.о. варианты стопроцентно исключают риск. Это значит, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Это свойство дозволяет считать ММ-критерий одним из базовых.
Применение ММ-критерия бывает оправдано, если ситуация, в какой принимается решение последующая:
1o
. О способности возникновения наружных состояний Fj
ничего не понятно;
2o
. Приходится считаться с возникновением разных наружных состояний Fj
;
3o
. Решение реализуется лишь один раз;
4o
. Нужно исключить какой бы то ни было риск.
2. Аспект Байеса – Лапласа.
Обозначим через qi
– возможность возникновения наружного состояния Fj
.
Соответственное правило выбора можно интерпретировать последующим образом:
матрица решений дополняется ещё одним столбцом содержащим математическое ожидание значений каждой из строк. Выбираются те варианты, в строчках которых стоит наибольшее
дополняется ещё одним столбцом содержащим математическое ожидание значений каждой из строк. Выбираются те варианты, в строчках которых стоит наибольшее
При всем этом предполагается, что ситуация, в какой принимается решение, характеризуется последующими обстоятельствами:
1о
. Вероятности возникновения состояния Fj
известны и не зависят от времени.
2о
. Решение реализуется (на теоретическом уровне) нескончаемо много раз.
3о
. Для малого числа реализаций решения допускается некий риск.
При довольно большенном количестве реализаций среднее
Т.о. аспект Байеса-Лапласа (B-L-критерий) наиболее оптимистичен, чем минимаксный аспект, но он подразумевает огромную информированность и довольно долгосрочную реализацию.
3о
. Аспект Сэвиджа.

Величину aij
можно трактовать как наибольший доп выигрыш, который достигается, если в состоянии Fj
заместо варианта Ei
выбирать иной, лучший для этого наружного состояния вариант. Величину aij
можно интерпретировать и как утраты (штрафы) возникающие в состоянии Fj
при подмене рационального для него варианта на вариант Ei
. В крайнем случае eir
представляет собой очень вероятные (по всем наружным состояниям Fj
, j = ) утраты в случае выбора варианта Ei
) утраты в случае выбора варианта Ei
.
Соответственное аспекту Сэвиджа правило выбора сейчас трактуется так:
1). Любой элемент матрицы решений  вычитается из большего результата maxeij
вычитается из большего результата maxeij
соответственного столбца.
2). Разности aij
образуют матрицу остатков . Эта матрица дополняется столбцом больших разностей eir
. Эта матрица дополняется столбцом больших разностей eir
. Выбирают те варианты, в строчках которых стоит меньшее для этого столбца
Требования, предъявляемые к ситуации, в какой принимается решение, совпадают с требованием к ММ-критерию.
4о
. Пример и выводы.
Из требований, предъявляемых к рассмотренным аспектам становится ясно, что в следствии их жёстких начальных позиций они применимы лишь для идеализированных практических решений. В случае, когда вероятна очень мощная идеализация, можно использовать сразу поочерёдно разные аспекты. Опосля этого посреди нескольких вариантов ЛПР волевым способом выбирает окончательное решение. Таковой подход дозволяет, во-1-х, лучше просочиться во все внутренние связи задачи принятия решений и, во-2-х, ослабляет воздействие личного фактора.
Пример. При работе ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) нужно временами приостанавливать обработку инфы и инспектировать ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) на наличие в ней вирусов. Приостановка в обработке инфы приводит к определённым экономическим издержкам. В случае же если вирус впору найден не будет, вероятна утрата и некой части инфы, что приведёт и ещё к огромным убыткам.
Варианты решения таковы:
Е1
– полная проверка;
Е2
– малая проверка;
Е3
– отказ от проверки.
ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) может находиться в последующих состояниях:
F1
– вирус отсутствует;
F2
– вирус есть, но он не успел разрушить информацию;
F3
– есть файлы, нуждающиеся в восстановлении.
Результаты, включающие Издержки на поиск вируса и его ликвидацию, также Издержки, связанные с восстановлением инфы имеют вид:
Таблица 1.
ММ-критерий
аспект B-L
F1
F2
F3
eir
= eij
eij
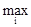 eir
eir
eir
=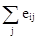
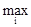 eir
eir
E1
-20.0
-22.0
-25.0
-25.0
-25.0
-22.33
E2
-14.0
-23.0
-31.0
-31.0
-22.67
E3
0
-24.0
-40.0
-40.0
-21.33
-21.33
Согласно ММ-критерию следует проводить полную проверку. Аспект Байеса-Лапласа, в предположении, что все состояния машинки равновероятны.
P(Fj
) = qj
= 0.33,
рекомендуется отрешиться от проверки. Матрица остатков для этого примера и их оценка (в тыщах) согласно аспекту Сэвиджа имеет вид:
Аспект Сэвиджа
F1
F2
F3
eir
= aij
aij
 eir
eir
E1
+20.0
0
0
+20.0
E2
+14.0
+1.0
+6.0
+14.0
+14.0
E3
0
+2.0
+15.0
+15.0
Пример специально подобран так, что любой аспект дает новое решение. Неопределённость состояния, в каком проверка застаёт ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач), преобразуется в неясность, какому аспекту следовать.
Так как разные аспекты соединены с разными критериями, в каких принимается решение, наилучшее всего для сравнительной оценки советы тех либо других критериев получить доп информацию о самой ситуации. А именно, если принимаемое решение относится к соткам машин с схожими параметрами, то рекомендуется использовать аспект Байеса-Лапласа. Если же число машин не велико, лучше воспользоваться аспектами минимакса либо Севиджа.
Производные аспекты.
1о
. Аспект Гурвица.
Стараясь занять более уравновешенную позицию, Гурвиц представил оценочную функцию, которая находится кое-где меж точкой зрения последнего оптимизма и последнего пессимизма:
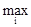 eir
eir
= {C eij
eij
+ (1- C)  eij
eij
},
где С– весовой множитель.
правило выбора согласно аспекту Гурвица, формируется последующим образом:
матрица решений  дополняется столбцом, содержащим среднее взвешенное меньшего и большего результатов для каждой строчки. Выбираются лишь те варианты, в строчках которых стоят самые большие элементы eir
дополняется столбцом, содержащим среднее взвешенное меньшего и большего результатов для каждой строчки. Выбираются лишь те варианты, в строчках которых стоят самые большие элементы eir
этого столбца.
При С=1 аспект Гурвица преобразуется в ММ-критерий. При С = 0 он преобразуется в аспект “азартного игрока”
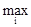 eir
eir
= 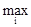
 eij
eij
,
т.е. мы становимся на точку зрения азартного игрока, делающего ставку на то, что «выпадет» наивыгоднейший вариант.
В технических приложениях трудно избрать весовой множитель С, т.к. тяжело отыскать количественную характеристику для тех толикой оптимизма и пессимизма, которые находятся при принятии решения. Потому почаще всего С := 1
/2
.
Аспект Гурвица применяется в случае, когда :
о вероятностях возникновения состояния Fj
ничего не понятно;
с возникновением состояния Fj
нужно считаться;
реализуется лишь маленькое количество решений;
допускается некий риск.
2о
. Аспект Ходжа–Лемана.
Этот аспект опирается сразу на ММ-критерий и аспект Баеса-Лапласа. При помощи параметра n выражается степень доверия к применяемому распределений вероятностей. Если доверие велико, то доминирует аспект Баеса-Лапласа, в неприятном случае – ММ-критерий, т.е. мы отыскиваем
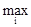 eir
eir
= 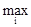 {n
{n + (1-n)
+ (1-n)  eir
eir
}, 0 £n£ 1. 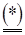
правило выбора, соответственное аспекту Ходжа-Лемана формируется последующим образом:
матрица решений  дополняется столбцом, составленным из средних взвешенных (с весом nºconst) математическое ожиданиями и меньшего результата каждой строчки
дополняется столбцом, составленным из средних взвешенных (с весом nºconst) математическое ожиданиями и меньшего результата каждой строчки
. Отбираются те варианты решений в строчках которого стоит набольшее
При n = 1 аспект Ходжа-Лемана перебегает в аспект Байеса-Лапласа, а при n = 0 становится минимаксным.
Выбор n субъективен т. к. Степень достоверности какой-нибудь функции распределения – дело тёмное.
Для внедрения аспекта Ходжа-Лемана лучше, чтоб ситуация в какой принимается решение, удовлетворяла свойствам:
вероятности возникновения состояния Fj
неопознаны, но некие догадки о распределении вероятностей вероятны;
принятое решение на теоретическом уровне допускает нескончаемо много реализаций;
при малых числах реализации допускается некий риск.
3о
. Аспект Гермейера.
Этот аспект нацелен на величину утрат, т.е. на отрицательные значения всех eij
. При всем этом
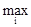 eir
eir
= 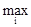
 eij
eij
qj
.
Т.к. в хозяйственных задачках в большей степени имеют дело с ценами и затратами, условие eij
<0 обычно производится. В случае же, когда посреди величин eij
встречаются и положительные значения, можно перейти к строго отрицательным значениям при помощи преобразования eij
— a при пригодном образом подобранном a> 0. При всем этом лучший вариант решения зависит от а.
правило выбора согласно аспекту Гермейера формулируется последующим образом :
матрица решений  дополняется ещё одним столбцом содержащим в каждой строке меньшее произведение имеющегося в ней результата на возможность соответственного состояния Fj
дополняется ещё одним столбцом содержащим в каждой строке меньшее произведение имеющегося в ней результата на возможность соответственного состояния Fj
. Выбираются те варианты в строчках которых находится наибольшее
В котором-то смысле аспект Гермейера обобщает ММ-критерий: в случае равномерного распределения qj
=  , j =
, j = , они стают схожими.
, они стают схожими.
Условия его применимости таковы :
вероятности возникновения состояния Fj
неопознаны;
с возникновением тех либо других состояний, раздельно либо в комплексе, нужно считаться;
допускается некий риск;
решение может реализоваться один либо пару раз.
Если функция распределения известна не весьма надёжно, а числа реализации малы, то, следуя аспекту Гермейера, получают, совершенно говоря, необоснованно большенный риск.
4о
.
BL
(
MM
) — аспект.
Рвение получить аспекты, которые бы лучше приспосабливались к имеющейся ситуации, чем все до сего времени рассмотренные, привело к построению так именуемых составных критериев. В качестве примера разглядим аспект, приобретенный методом объединения критериев Байеса-Лапласа и минимакса.
правило выбора для этого аспекта формулируется последующим образом:
матрица решений  дополняется еще 3-мя столбцами. В первом из их записываются математические ожидания каждой из строк, во 2-м — разность меж опорным значением
дополняется еще 3-мя столбцами. В первом из их записываются математические ожидания каждой из строк, во 2-м — разность меж опорным значением

и минимальным значением
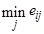
соответственной строчки. В 3-ем столбце помещаются разности меж большим значением
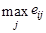
каждой строчки и большим значением  той строчки, в какой находится . Выбираются те варианты, строчки которых (при соблюдении приводимых ниже соотношений меж элементами второго и третьего столбцов) дают наибольшее математическое ожидание. А конкретно, соответственное
той строчки, в какой находится . Выбираются те варианты, строчки которых (при соблюдении приводимых ниже соотношений меж элементами второго и третьего столбцов) дают наибольшее математическое ожидание. А конкретно, соответственное
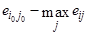
из второго столбца обязано быть либо равно некому заблаговременно данному уровню риска  . больше значения из второго столбца.
. больше значения из второго столбца.
Применение этого аспекта обосновано последующими признаками ситуации, в какой принимается решение:
вероятности возникновения состояний Fj
неопознаны, но имеется некая априорная информация в пользу какого-нибудь определенного распределения;
нужно считаться с возникновением разных состояний как по отдельности, так и в комплексе;
допускается ограниченный риск;
принятое решение реализуется один раз либо неоднократно.
BL(MM)-критерий отлично адаптирован для построения практических решений до этого всего в области техники и может считаться довольно надежным. Но данные границы риска  и, соответственно, оценок риска
и, соответственно, оценок риска  не учитывает ни число внедрения решения, ни иную схожую информацию. Воздействие личного фактора хотя и ослаблено, но не исключено стопроцентно.
не учитывает ни число внедрения решения, ни иную схожую информацию. Воздействие личного фактора хотя и ослаблено, но не исключено стопроцентно.
Условие
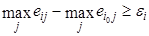
значительно в тех вариантах, когда решение реализуется лишь один либо маленькое число раз. В этих критериях недостаточно ориентироваться на риск, связанный лишь с нерентабельными наружными состояниями и средними значениями. Из-за этого, правда, можно понести некие утраты в успешных наружных состояниях. При большенном числе реализаций это условие перестает быть таковым уж принципиальным. Оно даже допускает разумные кандидатуры. При всем этом не понятно, но, точных количественных указаний, в которых вариантах это условие следовало бы опускать.
5о
. Аспект произведений.
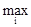 eir
eir
:= 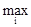
 eij
eij
правило выбора в этом случае формулируется так :
Матрица решений  дополняется новеньким столбцом, содержащим произведения всех результатов каждой строчки. Выбираются те варианты, в строчках которых находятся самые большие значения этого столбца.
дополняется новеньким столбцом, содержащим произведения всех результатов каждой строчки. Выбираются те варианты, в строчках которых находятся самые большие значения этого столбца.
Применение этого аспекта обосновано последующими обстоятельствами :
вероятности возникновения состояния Fj
неопознаны;
с возникновением всякого из состояний Fj
по отдельности нужно считаться;
аспект применим и при малом числе реализаций решения;
некий риск допускается.
Аспект произведений адаптирован сначала для случаев, когда все eij
положительны. Если условие положительности нарушается, то следует делать некий сдвиг eij
+ а с некой константой а > ï eij
eij
ï. Итог при всем этом будет, естественно зависеть от а. На практике почаще всего
а := ï eij
eij
ï+1.
Если же никакая константа не быть может признана имеющей смысл, то аспект произведений не применим.
Пример.
Разглядим этот же пример (табл. 1).
Построение рационального решения для матрицы решений о проверках по аспекту Гурвица имеет вид (при С =0.5, в 103
):
х
С eij
eij
(1-С) eij
eij
eir
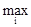 eir
eir
-20.0
-22.0
-25.0
-12.5
-10.0
-22.5
-14.0
-23.0
-31.0
-15.5
-7.0
-22.5
0
-24.0
-40.0
-20.0
0
-20.0
-20.0
В данном примере у решения имеется поворотная точка относительно весового множителя С : до С = 0.57 в качестве рационального выбирается Е3
, а при огромных значениях – Е1
.
Применение аспекта Ходжа-Лемана (q = 0.33, n = 0.5, в 103
) :
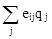
 eij
eij
n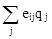
(1-n) eij
eij
eir
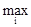 eir
eir
-22.33
-25.0
-11.17
-12.5
-23.67
-23.67
-22.67
-31.0
-11.34
-15.5
-26.84
-21.33
-40.0
-10.67
-20.0
-30.76
Аспект Ходжа-Лемана советует вариант Е1
(полная проверка) – так же как и ММ-критерий. Смена рекомендуемого варианта происходит лишь при n = 0.94. Потому равномерное распределение состояний рассматриваемой машинки обязано распознаваться с весьма высочайшей вероятностью, чтоб его можно было избрать по большему математическому ожиданию. При всем этом число реализаций решения постоянно остаётся произвольным.
Аспект Гермейера при qj
= 0.33 даёт последующий итог (в  ):
):

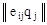
eir
= eij
eij
qj
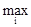 eir
eir
-20.0
-22.0
-25.0
-6.67
-7.33
-8.33
-8.33
-8.33
-14.0
-23.0
-31.0
-4.67
-7.67
-10.33
-10.33
0
-24.0
-40.0
0
-8.0
-13.33
-13.33
В качестве рационального выбирается вариант Е1
. Сопоставление вариантов при помощи величин eir
указывает, что метод деяния аспекта Гермейера является даже наиболее гибким, чем у ММ-критерия.
В таблице, приведенной ниже, решение выбирается в согласовании с BL(MM)-критерием при q1
=q2
=q3
=1
/2
(данные в 103
).
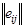
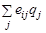
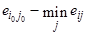
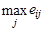
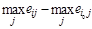
-20.0
-22.0
-25.0
-23.33
0
-20.0
0
-14.0
-23.0
-31.0
-22.67
+6.0
-14.0
+6.0
0
-24.0
-40.0
-21.33
+15.0
0
+20.0
Вариант Е3
(отказ от проверки) принимается сиим аспектом лишь тогда, когда риск приближается к  . В неприятном случае хорошим оказывается Е1
. В неприятном случае хорошим оказывается Е1
. В почти всех технических и хозяйственных задачках допустимый риск бывает намного ниже, составляя обычно лишь незначимый процент от общих издержек. В схожих вариантах бывает в особенности ценно, если некорректное заблаговременно, не зависимо от принимаемого решения, то посодействовать может вычисление ожидаемого риска  . Тогда становится вероятным пошевелить мозгами, оправдан ли схожий риск. Такое исследование обычно дается легче.
. Тогда становится вероятным пошевелить мозгами, оправдан ли схожий риск. Такое исследование обычно дается легче.
Результаты внедрения аспекта произведения при а = 41×103
и а = 200×103
имеют вид :
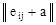
eir
= eij
eij
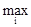 eir
eir
+21
+19
+16
6384
6384
а=41
+27
+18
+10
4860
+41
+17
+1
697
+180
+178
+175
5607
а=200
+186
+177
+169
5563
+200
+176
+160
5632
5632
Условие eij
> 0 для данной матрицы не выполнимо. Потому к элементам матрицы добавляется (по наружному произволу) поначалу а = 41×103
, а потом а = 200×103
.
Для а = 41×103
хорошим оказывается вариант Е1
, а для а = 200×103
– вариант Е3
, так что зависимость рационального варианта от а явна.
]]>

 (5 оценок, среднее: 4,80 из 5)
(5 оценок, среднее: 4,80 из 5)