Учебная работа. Реферат: Волновая оптика

(Пока оценок нет)

Загрузка...

Учебная работа. Реферат: Волновая оптика

свет как электромагнитные волны

Оптика – это учение о физических явлениях, связанных с распространением коротких электромагнитных волн, длина которых составляет приблизительно 10-5
– 10-7
м. Значение именно этой области спектра электромагнитных волн связанно с тем, что внутри неё в узком интервале длин волн от 0,4 до 0,76 мкм лежит участок видимого света, непосредственно воспринимаемого человеческим глазом. С точки зрения физики происходящих процессов выделение столь узкой области видимого света не имеет особого смысла, поэтому в понятие ,,оптический диапазон” включают обычно ещё и инфракрасное и ультрафиолетовое излучение. Но и для них принятые границы спектра достаточно условны. По существу, эти границы определяются используемыми способами получения и регистрации электромагнитных волн.

Излучение электромагнитных волн происходит при ускоренном движении электрических зарядов. Электромагнитные волны радиодиапазона излучаются антеннами радиопередатчиков при вынужденных колебаниях электронов в антеннах. Все электроны в антенне совершают колебания в одинаковой фазе. Поскольку эти колебания могут поддерживаться очень долго и с высоким постоянством частоты, то излучаемые при этом радиоволны с огромной степенью точности можно считать монохроматическими.

В оптике всё иначе. Любой источник света – это скопление множества возбуждённых или непрерывно возбуждаемых атомов. генератор световой волны – это каждый отдельный атом вещества. Возбуждённый атом излучает цуг почти монохроматических волн конечной протяжённости. характерной особенностью каждого элементарного источника является его самостоятельность, независимость от других атомов. Поэтому даже в том случае, когда отдельные цуги можно характеризовать одной и той же длиной волны λ, соотношение фаз между цугами волн, излученных разными атомами, имеют совершенно случайный характер и непрерывно меняются. Только в лазере, где используется вынужденное излучение, удаётся заставить все возбуждённые атомы излучать электромагнитные волны согласованно, подобно тому как это происходит в антенне радиопередатчика. В результате образуется световая волна, близкая по своим свойствам к идеальной монохроматической, – когерентная электромагнитная волна. Излучение обычных источников света, таких, как раскаленные твёрдые или жидкие тела, возбуждённые электрическим разрядом газы и т. д., представляет собой наложение огромного числа не согласованных между собой цугов волн, т. е. фактически ,,световой шум” – беспорядочные, некогерентные колебания электромагнитного поля.

наблюдать интерференцию света от таких некогерентных источников можно, только используя специальные приёмы – разделяя исходный пучок на два. Хотя в каждом из этих пучков, как и в исходном, фазовые соотношения между различными цугами непрерывно хаотически меняются, эти изменения будут одинаковыми для обоих пучков. Если эти пучки снова свести вместе, то можно наблюдать устойчивую интерференционную картину при условии, что разность хода между пучками не превышает длины отдельного цуга. Если же разность хода окажется больше длины цуга, то устойчивой интерференционной картины не будет, так как в этом случае будет происходит наложение цугов, излученных разными атомами.

Интерференция

Явление интерференции света впервые было объяснено на основе волновых представлений Юнгом в 1802 году. В произведённом им опыте малое отверстие А
в непрозрачном экране освещалось интенсивным источником света.

Принцип Гюйгенса
: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн даёт положение волнового фронта в следующий момент времени.
На основании принципа Гюйгенса это отверстие можно считать новым точечным источником полусферических волн. Эти волны падают на два малых отверстия S
1
и S
2
в следующем экране, которые в свою очередь становятся новыми точечными источниками волн.

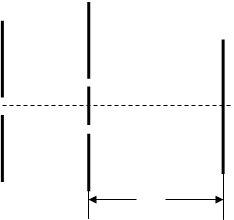
Таким способом в опыте Юнга достигается разделение исходной волны на две. Эти волны налагаются друг на друга в области за отверстиями и могут интерферировать, так как источники S
1
и S
2
когерентны. На экране В
образуется интерференционная картина.

Разделение волны от первичного некогерентного источника на две когерентные волны, т. е. получение двух вторичных когерентных источников, может осуществляться разными способами. Но расчёт интерференционной картины во всех таких случаях производится одинаково, так же, как и в схеме Юнга. Если в излучении первичного источника все независимые цуги волн характеризуются одной и той же длиной волны λ, то для излучения вторичных источников S
1
и S
2
можно использовать монохроматическую идеализацию, несмотря на то, что их излучение также представляет собой ту же хаотическую последовательность отдельных цугов. замена такой последовательности цугов бесконечной синусоидальной волной возможна здесь потому, что точечные вторичные источники когерентны, а разность хода излучаемых ими волн в любой точке экрана В
меньше протяжённости отдельного цуга. Для этого разумеется, экран В
должен быть удалён от источников S
1
и S
2
на значительное расстояние L
, а расстояние d
между источниками S
1
и S
2
должно быть достаточно мало.

Схема расчёта интерференционной картины
:

В точке О
, расстояния до которой от источников S
1
и S
2
одинаковы, приходящие волны усиливают друг друга, так как колебания поля в этой точке происходят в одинаковой фазе. Результат сложения колебаний в произвольной точке Р
определяется разностью хода l
волн, приходящих в Р
из S
1
и S
2
. Если l
равно целому числу длин волн λ, то колебания в Р
усиливают друг друга; если l
равно нечётному числу полуволн, то колебания взаимно ослабляются.

Выразим разность хода l
волн, приходящих в точку Р
, через угол θ
между осью и направлением на точку Р
и расстояние d
между источниками.

Будем считать, что d
<<L
. Тогда при малых θ
разность хода можно найти, опуская из S
1
перпендикуляр на прямую S
2
Р
: l=dθ
.

Эта формула даёт возможность определить угловое положение максимумов и минимумов на экране В. направление на максимумы получим, полагая что l=nλ
: θ
max

=nλ/d
,
n=0
, ±
1, ±2,…

Полагая, что l=(2n+1)λ
/
2
,
получим направления на минимумы: θ
min

=(n+1/2)λ/d
,
n=0
,
±1, ±2,…

Угловое расстояние Δθ
между соседними максимумами или минимумами, как видно из этих формул, равно λ/d
, а расстояние h
между ними на экране В, как видно из рис., равно h=L
Δθ=λL/d

Дифракция

характерной особенностью дифракционных явлений в оптике оказывается то, что здесь, как правило, длина волны света почти всегда много меньше размеров преград на пути световых волн. поэтому наблюдать дифракцию света можно только на достаточно больших расстояниях от преграды. Проявление дифракции состоит в том, что распределение освещённости отличается от простой картины, предсказываемой геометрической оптикой на основе прямолинейного распространения света.

Строгий расчёт дифракционной картины представляет собой очень сложную математическую задачу. Но в некоторых практически важных случаях достаточно хорошее приближение даёт упрощенный подход, основанный на использовании принципа Гюйгенса – Френеля.

Согласно этому принципу, световая волна, возбуждаемая каким-либо источником S
, может быть представлена как результат суперпозиции когерентных вторичных волн, ,,излучаемых” фиктивными источниками. такими источниками могут служить физически бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S
. Обычно в качестве этой поверхности, выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предложил, что если между источником и точкой наблюдения находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии – такая же, как при отсутствии экрана.

Учёт амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т.е. определить закономерности распространения света.

Дифракция Френеля на круглом отверстии
:

Сферическая волна, распространяющаяся из точечного источника S
, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S
с центром отверстия. Экран параллелен плоскости отверстия и находится от него на расстоянии b
. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Для точки В, согласно методу зон Френеля, амплитуда результирующего колебания A=A1
/2±Am
/2
, где знак плюс соответствует нечётным т
и минус – чётным т
.

Когда отверстие открывает нечётное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны, если чётное, то амплитуда (интенсивность) будет равна нулю. Если в отверстие укладывается одна зона Френеля, то в точке В амплитуда A=A1

, т.е. вдвое больше, чем в отсутствии непрозрачного экрана с отверстием (интенсивность света больше соответственно в четыре раза). Если в отверстие укладывается две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т
чётное, то в центре будет темное кольцо, если т
нечётное – светлое кольцо), причем интенсивность максимумов убывает с расстоянием от центра картины.

Расчёт амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены (число зон Френеля, укладывающихся в отверстии, зависит от λ
).

Дифракция Френеля на диске
. Сферическая волна, распространяющаяся от точечного источника S
, встречает на своем пути диск. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S
с центром диска. В данном случае закрытый диском участок фронта волны надо исключить из рассмотрения и зоны Френеля строить начиная с краёв диска.

Пусть диск закрывает т
первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна

A=Am+1
– Am+2
+ Am+3
—
…=
Am+1
/2+(Am+1
/2 – Am+2
+Am+3
/2)+
…
, или A=Am+1
/2
, так как выражения, стоящие в скобках, равны нулю. следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружён концентрическими с ним тёмными и светлыми кольцами, а интенсивность максимумов убывает с расстоянием от центра картины.

задача

.
Два груза D
и E
массами т
D

=0,25
кг
и тЕ
=3 кг
лежат на гладкой плоскости, наклонной под углом α=30°
к горизонту, опираясь на пружину, коэффициент жёсткости которой с=6 Н/см =600 Н/м.

В некоторый момент груз Е
убирают; одновременно (t=0
) нижний конец пружины В
начинает совершать вдоль наклонной плоскости движение по закону ξ
=0,02
sin 10t
(м). Найти уравнение движения груза D
.

Решение
. Применим к решению задачи дифференциальные уравнения движения точки. Совместим начало координатной системы с положением покоя груза D
, соответствующим статической деформации пружины, при условии, что точка В
занимает своё среднее положение (ξ=0)
.

Направим ось x
вверх вдоль наклонной плоскости (в сторону движения груза D
после снятия груза Е
). Движение груза D
определяется по следующему дифференциальному уравнению: mD
x=∑Xi

,

где ∑Xi

– сумма проекций на ось х
сил, действующих на груз D
(рис. а): GD
–
веса, N
–
нормальной реакции наклонной плоскости, Р
– силы упругости пружины.

таким образом, mD
x = -GD
sin α – P
.

Здесь P = c(x – f
ст
D

– ξ)
, где f
ст
D

– статическая деформация пружины под действием груза D
; ξ
– перемещение точки прикрепления нижнего конца пружины, происходящее по закону ξ =
d sin pt (d =0,02
м, p=10
рад/с).

Статическая деформация пружины f
ст
D

найдём из уравнения, соответствующего состоянию покоя груза D
на наклонной плоскости (рис. б):

∑Xi
=0;

-GD
sin α +P0
=0,

т. е. –GD
sin α + cf
ст
D

=0,

откуда f
ст
D

=GD
sin α/c.

Дифференциальное уравнение движения груза D
имеет вид

mD
x = -GD
sin α – c(x – f
ст
D

– ξ),

или после преобразования mD
x + cx = cd sin pt.

Разделив все члены уравнения на mD

и введя обозначения

c/mD
= k2
, cd/mD

= h,

приведём дифференциальное уравнение к следующему виду:

x + k2
x = h sin pt.

Решение этого неоднородного уравнения складывается из общего решения х*
, соответствующего однородного уравнения и частного решения х**
данного неоднородного уравнения:

x = x*+ x**.

Общее решение однородного уравнения имеет вид

x* = C1
cos kt +C2
sin kt.

частное решение неоднородного уравнения:

x** = [ h /(k2
– p2
)] sin pt.

Общий интеграл

x = C1
cos kt +C2
sin kt + [ h /(k2
– p2
)] sin pt.

Для определения постоянных интегрирования С1

и С2

найдём, кроме того, уравнение для х

x = -C1
k sin kt +C2
k cos kt + [ hp/(k2
– p2
)] cos pt

и используем начальные условия задачи.

Рассматриваемое движение начинается в момент (t=0)
, когда деформация пружины является статической деформацией под действием грузов D
и E
. При принятом положении начала отсчёта О
начальная координата груза D
равна x0
= -f
ст
E

, причем f
ст
E

= GE
sin α/c
– статическая деформация пружины под действием груза Е
.