Учебная работа. Статья: Використання енергії хвиль системою осцилюючих поверхневих розподілів тиску

Учебная работа. Статья: Використання енергії хвиль системою осцилюючих поверхневих розподілів тиску

Використання енергії хвиль системою осцилюючих поверхневих розподілів тиску

Вступ

Ряд пристроїв хвильової енергії, у цей час розглянуті і у Великобританії, і в іншому місці мають режим роботи, який базується на наступному принципі. Область вільної поверхні оточена твердою порожньою плаваючою структурою, відкритою на зануреному кінці днища, який захоплює об’єм повітря вище цієї внутрішньої вільної поверхні. Область набігаючої хвилі створює підвищення та падіння вільної поверхні, і об’єм повітря приводить у рух назад і вперед з високою швидкістю через стиск, що містить повітряну турбіну, яка живить генератор для прямого перетворення в електрику. У моделі повітряна турбіна замінена простою пластиною з отвором — розмір отвору регулюється так, щоб відповідати характеристикам турбіни в повному масштабі. Приклади пристроїв, які працюють на цьому принципі — C.E.G.B. пристрій (Коунт та ін. 1981), буй був розроблений Королівським Університетом, Белфаст, та опротестований в Японії. Описи цих двох пристроїв можна знайти в Кварела (1978).

При дослідженні гідродинамічної моделі таких пристроїв, автори використали теорію, розроблену до пристроїв хвильової енергії, які включають тверді коливні тіла і описані, наприклад, в Еванса (1981). Це звичайно включає заміну вільної поверхні невагомим поршнем і вимагає визначення додаткової маси і демпфування поршня. Приклади такого підходу, який нехтує будь-яким просторовими змінами у внутрішній вільній поверхні, викликані поверхневим тиском, в Еванса (1978), який розглядає резонансні коливання вузького водного стовпа в зануреній відкритій вертикальній трубі, Коунт та ін. (1981), які обчислюють гідродинамічний коефіцієнт для C.E.G.B. пристроя енергії хвилі, який може бути точно описаний як напіввідкрита сірникова коробка, що пливе догори ногами на водній поверхні. Ця стаття представляє більш точну та більш просту теорію для таких пристроїв, яка правильно враховує прикладений поверхневий тиск і послідовну просторову зміну внутрішньої вільної поверхні.

Подібний підхід до двовимірної задачі хвильової енергії був зроблений Фалькао та Сарменто (1980), продовжуючи роботу Стокера (1957). Дана робота узагальнює їхні результати для довільних розподілів тиску як для двох так і трьох вимірного випадку. У іншому контексті Огільві (1969) також розглянув деякі двовимірні задачі, які включають області тиску. Отримані результати він використав для передбачення руху довгого транспортного засобу з повітряною подушкою. Він також вирішив явно важку задачу однорідної області тиску по частині поверхні, яка обмежена двома однаково зануреними вертикальними пластини. Обчислення рішення не проводилось.

Загальна теорія розроблена в § 2 та використані результати для гіпотетичного максимального поглинання енергії довільної системи поглинаючих енергію розподілів тиску. Близька подібність до відповідних результатів з теорії твердих тіл пропонує різні взаємовідношення між деяким випромінюванням та розсіюванням задачі, які належним чином доведені в додатку. Прості спеціальні випадки, які ілюструють загальну теорію, представлені в §2 та §3, де до того ж практичніші міркування забезпечують умови резонансу. В §4 зроблено порівняння з резонансними умовами теорії твердого тіла і представлені криві максимальної ширини поглинання в кожному випадку для окремого круглого поверхневого тиску або твердого диска.

1. Формулювання

Для установки ідеї, ми розглядаємо встановлену структуру відкритою на задньому кінці і закритою на передньому кінці, який перетинає вільну поверхню, захоплюючи обсяг повітря в ряд ізольованих секцій, кожна має свою власну внутрішню вільну поверхню. Ефект ряду набігаючих хвиль змушує внутрішні вільні поверхні коливатися з тією ж частотою, як і набігаюча хвиля, змушуючи їх повітряні обсяги рухатися назад і вперед через стискувачі, які містяться в турбінах. Приймається, що стискаємість повітря маленька, таким чином, щоб повітряний тиск у кожній турбіні був такий же, як однорідний розподіл тиску трохи вище відповідної вільної поверхні. Повна середня оцінка виконання роботи буде сума середнього часу вироблення цих тисків і об’ємів потоків через турбіни, що у свою чергу є тим самим, що й вироблення просторового середнього числа вертикальної швидкості кожної внутрішньої вільної поверхні і її областей. В даній роботі ми припускаємо, що характеристики турбіни лінійні так, що зниження тиску поперек турбіни пропорційне об’єму потоку через неї. Візьмемо декартову систему координат з осями x, y горизонтальними і віссю z вертикальною, з z= 0 незбуреною вільною поверхнею.

Відповідно до припущень про лінійну теорію водної хвилі, ми можемо скласти потенціал швидкості Ф(x, y, z, t) для задоволення задачі:

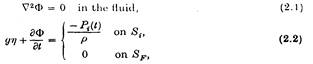
де Si — i – та внутрішня вільна поверхня, SF — зовнішня вільна поверхня, і h (x, y, t) – підйом поверхні, який задовольняє:

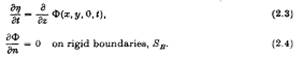
тут Рі(t) — поки ще невідомий простий гармонічний тиск на Si. Ефект структури частково розсіює набігаючи хвилі таким чином, щоб на більших відстанях, окрім потенціалу набігаючої хвилі, там виникала область хвилі, яка рухається далеко від структури. Потенціал набігаючої хвилі можна описати:

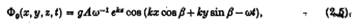
де

k = w2/g,

і набір набігаючих хвиль утворюють з позитивною віссю х кути b.

Рівняння (2.2) і (2.3) можна об’єднати, щоб отримати:

для простих гармонійних рухів.

Зручно писати:

де Фd позначає розсіяний позитивний набігаючий потенціал інциденту, який задовольняє (2.1), (2.4) і (2.6) з Рі (t) = 0 ; Y — випромінювальний потенціал, який задовольняє (2.1), (2.4) і (2.6), але який поводиться подібно відступаючим хвилям на більших відстанях. Тоді зрозуміло, що Ф як дана в (2.7) задовольнить всі умови задачі.

Тепер норма об’єму потоку через Si :

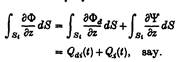
Тоді повна норма роботи сил тиску через всю Si :

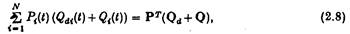
де P, Qd, Q, є векторами-стовбцями, в яких і – ті компоненти — Рі, Qdі та Qі відповідно. Тепер простий гармонічний тиск Рі(t) в Si — один даватиме збільшення норм обсягів потоку Qj (t) на Sj (j = 1, …, N), які є також простою гармонікою в часі. Робимо довільне але зручне розкладання:

де A, B — реальні симетричні матриці розмірністю NxN , з B коефіцієнтом демпфування, взагалі визначеним позитивним, який, в принципі, можна обчислити. Розкладання (2.9) можна порівняти з звичайним розкладанням сили на коливальному тілі в позначеннях доданої маси і матриць демпфування.

На цій стадії зручно представити незалежні від часу величини. Запишемо:

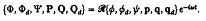
Потім усереднюючи період, середня норма роботи сил тиску стає:

Тут * означає сполучене транспонування.

У позначеннях незалежних від часу величинах (2.9) можна переписати:

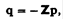
де

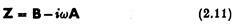
повна комплексна провідність. Тоді (2.10) стає:

де відмітимо, що А не з’являється. Вираз (2.12) можна переписати у вигляді:

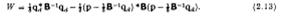
З цього випливає, що якщо B-1 існує:

де

Тоді б максимальна середня потужність була б досягнута впевненістю, що тиск в, скажемо, Si є лінійною комбінацією об’ємів потоків, які викликані в кожній S j , j = 1, …, N, через одну набігаючи позитивну розсіювану хвилю, пропорційні константи такі як в (2.15) задоволені. Результати (2.14) і (2.15) ідентичні відповідним виразам, отриманим для системи незалежно коливающихся тіл поглинання в наборі регулярних набігаючих хвиль. Тоді, ролі тиску та набігаючого хвильового об’єму потоку замінені швидкістю та набігаючою хвилею, яка збуджує силу на тілах.

Тепер практично, керувати об’ємом потоку через турбіни легше ніж через зниження тиску. Приймемо лінійне відношення між ними у вигляді:

де L — матриця розмірністю NxN. Помітьте, що знак перед L прийнятий позитивним тоді як, на відміну від (2.11), сили тиску і об’єми потоків вимірюються в напрямку вверх. Якщо це використати в об’єднанні з (2.11), отримаємо:

що з (2.15) показує:

для максимальної потужності. тут риска означає сполучений комплекс. Фактично (2.13) можна записати після деякої маніпуляції:

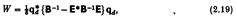
де

і застосовуємо (2.17). Ця форма показує явно імпеданс, який відповідає умові необхідній для оптимальності.

На жаль, у дійсності, якщо турбіни не зв’язані, кожна турбіна матиме свою власну характеристику тиск/потік, яка тут прийнята лінійною, таким чином, щоб L була діагональною матрицею, враховуючи, що B і А – повні матриці. Крім того, якщо характеристики насоса показують стадію затримки між тиском і об’ємом потоку, елементи L будуть реальні і позитивні. таким чином у частинному випадку вираз (2.19) повинен мати не нульовий елемент lі L. Навіть у найпростішому випадку, коли всі l ідентичні, не факт, що будь-який очевидний аналітичний метод максимізації (2.19) і числової оптимізації повинен використатися.

Тепер зрозумілий спосіб переходу до частинної задачі. Спочатку потрібно визначити складну матрицю повної провідності Z, або теоретично або експериментально. Це включає знаходження об’єму потоку, викликаного через весь Sj через однорідний розподіл тиску по кожному Sj почерзі. Потім qd , вимушений об’єм потоку через кожен Sj через окремий дифрагований потенціал, необхідно визначити і в результаті можна отримати середню потужність поглинання з (2.19) в позначеннях (прийнятих лінійними) характеристик турбіни змодельованих матрицею L.

Перед розглядом специфічних прикладів, цікаво розглянути теоретичний максимум потужності відповідно до припущення, що імпеданс може бути погоджений точно. Іншими словами ми припускаємо, що є механізм контролю, який гарантує, що L = Z таким чином, що об’єм потоку через Sj — визначена лінійна комбінація тисків у кожному Sj. У цьому випадку:

результат паралельний результату у теорії для систем незалежно коливающихся поглинаючих твердих тіл (Еванс 1979; Falnes 1980), де qd замінена збудженим вектором сили на системі тіл.

Тепер, в рівнянні додатка (А 27) показано, що елементи B пов’язані з елементами вектора qd таким чином, щоб необхідно було тільки визначити, вимушений об’єм потоку через кожну Sj завдяки дифрагованому потенціалу хвилі як в (А 17), для одержання елементів матриці демпфування B та результуючого Wmаx з (2.21). Тепер дифрагований потенціал виникає через присутність будь-якої встановленої твердої структури та не залежить від розподілів тиску. таким чином, фd , а отже qdi може бути визначене використовуючи існуючі дифракційні програми, звичайні в корабельній гідродинамічній теорії.

Подальше спрощення можливо, якщо можна припустити, що фіксована занурена частина поглинача – маленька осадка судна. Тоді єдиний гідродинамічний ефект структури повинен обмежити розмір і форму внутрішніх вільних поверхонь Sі. Але тепер оцінка qd тривіальна, оскільки вимагає тільки інтегрування набігаючого потенціалу по Si, оскільки розсіяним потенціалом можна знехтувати.

Як приклад загальної теорії ми розглядаємо тільки одну внутрішню вільну поверхню S1, так, щоб:

коли з (А1)

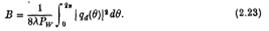
Якщо S1 та SB асиметричні таким чином, що qd не залежить від кута атаки, отримаємо:

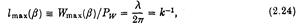
де l(b) означає ширину захвата для пристрою, і l — довжина набігаючої хвилі. Цей результат ідентичний отриманим для асиметричних окремих поглинаючих тіл коливання у вертикальних переміщеннях (Будал та Калнес 1975; Кванс 1970, Нюман 1976).

Для неасиметричних розподілів тиску, які мають нульову тягу подальше просування можна все ще зробити, використовуючи (2.23).

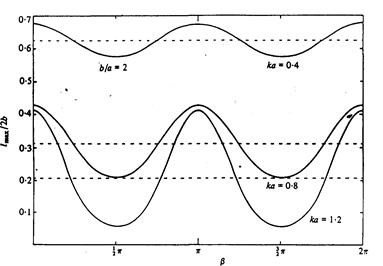
Рис.1. Зміна максимального відношення ширини захвата, lmax/2b з кутом атаки b для регулярних хвиль, які наближаються до прямокутного поглинаючого поверхневого розподілу тиску, для різних значень безрозмірного числового числа ka і b/a = 2. Пунктири показують асиметричні значення (2kb)-l

Ми маємо з (2.22) — (2.24):

Розглянемо окремий прямокутний розподіл тиску з нульовою тягою, яка охоплює S1 : |х|£а, |y|£ b. Тоді:

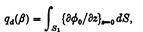
де

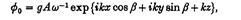
таким чином, що:

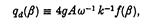
де

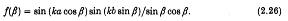
Цей простий вираз дозволяє зробити оцінку впливу форми і орієнтації окремого прямокутного розподілу тиску на ширині захвата максимальної потужності.

Зверніть увагу, що з (2.25):

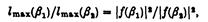
таким чином, що частинний випадок:

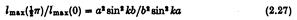
ілюструє відносну ефективність поверхні тиску в відходящих та зустрічних хвилях.

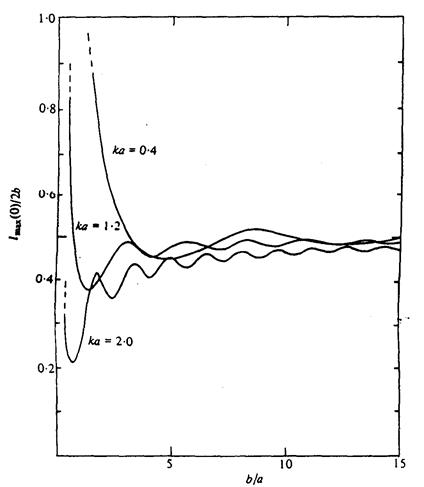
Рис. 2. Зміна відношення максимальної ширини захвата, lmax/2b з відносним подовженням b/a, для регулярних хвиль, які наближаються до прямокутного поглинаючого поверхневого розподілу тиску для різних значень безрозмірного хвильового числа ka.

Результати, які базуються на обчисленні рівнянь (2.25) — (2.27) даються на рис. 1 і 2. На рис. 1 ширина захвата безрозмірна відносно ширини пристрою 2b, зображена як функція кута атаки хвилі для випадку b/a = 2 і для різних значень ka. Не показаним є випадок b=a, де зміна lmax/2b з аксіально-симетричних результатів (2.24) є маленькою з оптимальним кутом атаки рівним b = ¼ p, коли гребені хвилі паралельні діагоналі квадрату. Як могло б очікуватися, коливання lmax/2b з b більші для більшого ka, оскільки прямокутна форма більше впливає на коротші хвилі. Наприклад аксіально-симетричний розподіл тиску має максимальну ширину захвата близько 5/8 діаметру в хвилях приблизно 8 розмірів діаметру (ka = 0,4). Для прямокутного розподілу тієї ж самої ширини але половини довжини (b/a = 2) збільшення в ширині захвата в убігаючих хвилях, b=0 °, є тільки приблизно 10 %. З іншого боку, для хвиль 4 розмірів діаметру (ka = 0, 8) ширина захвата збільшується приблизно до 60 % з 3/10 діаметру до приблизно 2/5 ширини пристрою. Оскільки з формули (2.26) ми знаходимо, що протилежний ефект відбувається в верхніх морях b = ½p, де прямокутний розподіл (з b/a® 1) завжди менш ефективний ніж аксіально-симетричний розподіл. Як відношення ширини захвату в убігаючих хвилях залежить від відносного подовження (b/a) прямокутного розподілу показано на рис. 2 для різних значень ka. Як могло б очікуватися, з b/a® ¥ відношення ширини захвата наближається до 0, 5, що є результатом для ефективності потужності поглинання двовимірним розподілом (див. рівняння (2.29)).

Результати, які відповідають двовимірним розподілам тиску можна отримати, повертаючись до (2.21) і використовуючи результати (А 32), (А 33), які дають:

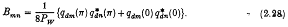
Знову, що стосується тривимірних розподілів тиску, для визначення значення максимальної ефективності, необхідно тільки вирішити єдину дифракційну задачу для розсіювання набору хвиль твердою частиною системи поверхонь тиску. Як тільки це визначено, qdm знаходиться з (А 17), а максимальна потужність поглинання з (2.21).

Значно спростити задачу, можна розглянувши випадок однієї поверхні тиску, тоді одержуємо ефективність потужності поглинання:

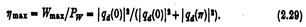
тут Wmах — інтерпретується як максимальна середня потужність поглинання одиницею ширини розподілу тиску.

Для хвиль, які наближаються з x = +¥ аргумент нумератора повинен бути замінений p. Альтернативний вираз:

( де f ± визначений з (А 28)), показує, як для твердого поглинача хвильової енергії у двох вимірах, що гарний нереверсивний генератор хвилі (у напрямку від того, де набігаюча хвиля прибуває) є гарним поглиначем.

Знову з (2.30) витікає, що для розподілу тиску, який симетричний щодо осі x, таким чином, що f + = f -, максимум ефективності є ½ , в той час як з (2.30) для довільного єдиного розподілу тиску:

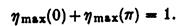
Для наступного найпростішого випадку двох розподілів тиску (N = 2), підстановка (2.28) в (2.21) дає, після деяких математичних перетворень:

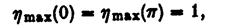
показує, що вся енергія набігаючих хвиль може бути поглинена. Цей результат забезпечує:

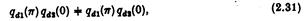
що є умовою, яка гарантує, що B-1 існує. З (А 34) рівняння (2.31), як видно, еквівалентне

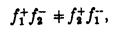
умова, яка зустрічається у випадку твердого тіла, як в Срокоза та Еванса (1979), так і в Коунта та Джеферса (1980), які вказують, що це виключає обидва способи, як симетричний (fт + = fт — ), так і або асиметричний (fт + = — fт — ).

Якщо N> 2 , формула (2.14) більше не застосовується, оскільки B автоматично сингулярне. Це випливає з того, що B можна записати:

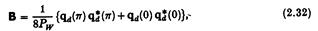
що показує, що B може мати порядок 2 та більше. Це твердження також отримане Коунто та Джеферсом (1980) в контексті твердого тіла.

Формула (2.32) забезпечує альтернативний вираз до (2.12) для середньої потужності, а саме:

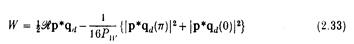
який є аналогічним отриманому Ньюманом (1976), рівняння (61а) для випадку твердого тіла, яке коливається багатьма способами.

Здається імовірно, що максимальна поглинальна ефективність для N> 2 є також одиничною, але загального доказу з (2.33) ще немає. Зрозуміло, однак, що оптимальні значення для p не будуть єдиними.

2. Умови резонансу

Максимум потужності поглинання, даний в (2.21). Однак, цього можна досягнути, якщо тільки ми можемо стверджувати, що L= Z. практично, малоймовірно що матриця L буде не реальна і діагональна з позитивними елементами. Ми розглядаємо значення цього для випадку єдиної внутрішньої вільної поверхні.

Ми маємо:

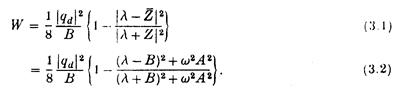
Для даних A, B, як функції w2a/g,

з

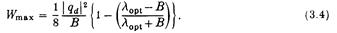
Для аксіально-симетричного розподілу тиску та зв’язаної структури, з (А 27)

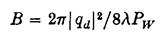
таким чином, що

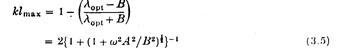
в той час для двовимірного симетричного розподілу тиску,

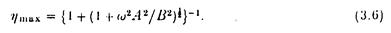
Зрозуміло, що цікаво установити, чи є значення w2a/g для якого А зникає, відповідно викликаючи об’єм потоку униз по поверхні перебуваючи в фазі з прикладеним тиском. Будемо розглядати два простих приклади, для яких можна отримати явні рішення.

(а) Двовимірна область хвилі, створена однорідним простим гармонічним тиском по кінцевому інтервалі |х| <а осі х , що представляє вільну поверхню вперше була вирішена Стокером (1957) і згодом розглянута Огільві (1969) та Фалькао і Сарменто (1980). Для цієї простої задачі маємо, (А32), (А33):

і це легко показує, що

оскільки там немає розсіяного потенціалу.

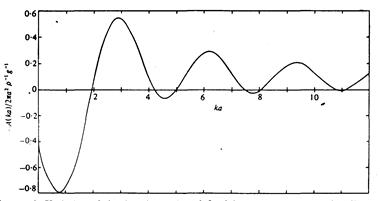
Рис. 3. Зміна функції А(ka), визначена рівнянням (3.10), з безрозмірним хвильовим числом ka, для круглого однорідного коливального поверхневого розподілу тиску радіусом a.

Вираз для А(ka) більше ускладнено, включаючи спеціальні функції Ci й Si. Однак Фалька і Сарменто (1980) показали, і це може бути підтверджене Огільві (1969), рис. 15, що А(kа) = 0 для ka = 1,3 відповідно до половини ширини смуги приблизно п’ята частина довжини хвилі. Рівняння (3.6) тепер показу, що зі збільшенням ka від нуля, максимальна ефективність 0,5 досягається приблизно при ka = 1,3 для А(ka)= 0, але ефективність знижується до нуля при наступних значеннях ka, для яких В(ka) = 0 , а саме ka = np, n = 1,2, … . Криві, які показують зміну hmax з ka даються Фалкао та Сарменто (1980).

(b) Як наступний приклад ми розглядаємо аксіально-симетричний розклад вищезгаданого до однорідного коливального розподілу тиску по диску радіусом а на вільній поверхні в глибокій воді. Результуючу тривимірну аксіально-симетричну область хвилі можна визначити явно, використовуючи теорему Гріна разом з фундаментальним потенціалом джерела хвилі в трьох вимірах або, більш просто, за допомогою перетворення Хенкеля.

Знайдено, що

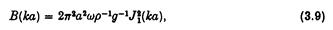
в той час:

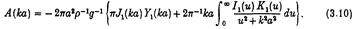
тут J1, Y1, I1, K1 — функції Бесселя у звичайному розумінні. Похідні цього результату разом з розкладами до кінцевої глибини і трубками, які пересікають поверхню води можна знайти у Томаса (1981)

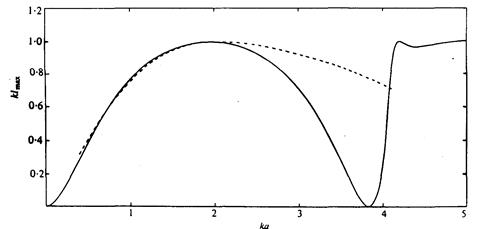
Рис. 4. Зміна klmax з безрозмірним хвильовим числом ka, для циркулярного поглинання коливальних поверхневих розподілів тиску (суцільна лінія) і циркулярного поглинання твердого диску (пунктирна лінія).

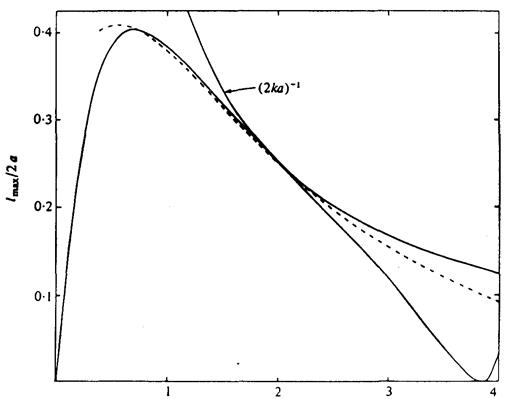
Рис. 5. Зміна безрозмірного відношення ширини захвату lmax/2a з безрозмірним хвильовим числом для циркулярного поглинання коливального поверхневого розподілу тиску (суцільна лінія) і циркулярного поглинання коливального твердого диску (пунктирна лінія). Також показаний теоретичний оптимум (2ka) -l у кожному випадку.

Граф виразу в фігурних дужках в (3.10) показаний на рис. 3 проти ka. Здається, що А(ka) має тільки сім нулів, перший з яких є ka = 1,96 відповідно до радіуса диску приблизно три десятки довжини хвилі. Перший нуль B (ka) відбувається в ka = 3,83.

На рис. 4 показана зміна klmax з ka в той час, як рис. 5 показує безрозмірну зміну ширини захвата щодо діаметру диска. Можна побачити, що максимальне значення klmаx відбувається в першому нулі поки klmах зменшується до нуля при ka = 3,83 відповідно до першого нуля B (ka). Наступні нулі А(ka), B (ka) викликають коливальну поведінку klmax зі збільшенням ka. Найкраще це показано при відношенні ширини захвата lmax/2a зі зміною ka. Ефект позначення, який включає А (ka) дає абсолютний максимум відношення ширини захвата приблизно 0,4 у потрібному діапазоні при ka == 0,7 або відношення довжини хвилі до діаметра приблизно 5. Також показана крива (2ka) -l отримана з (2.24), приймаючи, що резонанс може бути досягнутий при всіх частотах. Як очікується єдина точка контакту з кривою lmax/2a знаходиться в першому нулі А(ka).

3. Порівняння з твердою моделлю пластини

Попередні рішення пристроїв хвильової енергії, які базуються на ідеї форсування пійманого об’єму повітря на водній поверхні через турбіну, були змодельовані вільними поверхнями з умовою для твердої поверхні запропонованої вертикальної швидкості. Подивимось, наприклад, Коунта та ін. (1981). Там обговорювалось, що довгі хвилі принаймні (k® 0), умова тиску (2.6) зводиться до умови твердої поверхні. Однак, щоб бути послідовними, те ж саме наближення потрібно зробити по вхідній вільній поверхні, в якій випадок задачі елемента хвилі втрачений.

Цікаво спостерігати за розходженням результатів двох підходів. Ми розглядаємо тільки єдиний симетричний пристрій, який складається або з твердої поверхневої пластини або з розподілу тиску. В обох випадках максимальна ефективність рівна ½ в двох вимірах, або максимальна ширина захвата – k-l для аксіально-симетричних пристроїв.

Фактична ширина захвата для циркулярного поглинання пластини може бути записана (Еванс 1976) у формі, точно аналогічній (3.4), (3.5), де тепер l — позитивний коефіцієнт демпфування пропорційний швидкості, який з’єднує вертикальну конфронтуючу силу прикладену ззовні на диску та вертикальній швидкості диску. Крім того:

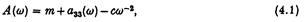
де т — маса диску, a33 (w) його частотно-залежні коливання доданої маси, і

c = pа2rg

коефіцієнт відновленої плавучості, відповідно до припущення, що диск на поверхні є частиною круглого циліндра з кінцевою довжиною, який знаходиться над поверхнею. Коефіцієнт B (w) = b33 (w) – частотно-залежний коефіцієнт демпфування для примусового коливального руху вертикальних коливань диска з одиничною амплітудою швидкості.

Тепер, оскільки прийнято, що диск лежить на вільній поверхні, його масу можна ігнорувати порівняно з його доданою масою, яка в свою чергу може бути безрозмірною, використовуючи запис а33 (w) = 2pа3rm3 (w) таким чином, що:

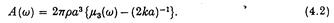
Подібно

B (w) = 2pа3r w l3 (w),

де l3 (w) — безрозмірний коефіцієнт демпфування.

Вертикальні коливання доданої маси і коефіцієнти демпфування для круглого доку на поверхні були визначені МакКамом (1961), хоча, здається, що на його рис. 6 і 7 є типографська помилка в позначенні ординат; асимптотичний результат m3 ~ 2/3p при ka®¥ разом з іншою інформацією пропонує, що значення дані для m3 та l3 повинні бути зменшені фактором 2p. З цим виправленням, знайдено, що А(w) зникає один раз тільки при ka = 2,1, в той час як B (w) завжди позитивне. Ефект цих розходжень на klmах та lmах /2a показується пунктирами на рис. 4 і 5.

Можна помітити з рис. 4, що у діапазоні 0 < ka < 4, який охоплює діапазон практичного інтересу для пристроїв хвильової енергії, головне розходження в klmaх відбувається для ka > 2, де значення розподілу тиску починають зменшуватися, досягаючи нуля при значенні ka = 3,82 відповідно до першого нуля B (ka) для цього випадку. Поки B (ka) не рівне нулю для твердого поверхневого доку, не відбувається ніякого зниження в klmах в цьому випадку. Те ж саме правильне для відношення ширини захвата на рис. 5; фактично для діапазону відношення довжини хвилі / діаметр від 1,5 до 4 розходження у двох відношеннях ширини захвату — маленькі.

Подібні розходження, які відбуваються у випадку двовимірної смуги також розглянуті МакКамом (1961). У цьому випадку с=2аrg в (4.1) і А(w) зникає для ka(=w2а/g) = 1,42 порівняно зі значенням 1,3, який передбачили Фалько та Сарменто (1980).

Висновок

Було розглянуто ряд задач, які стосуються поглинання енергії хвилі коливальними однорідними поверхневими розподілами тиску. Показано, що використовуючи лінеаризовану теорію водної хвилі можна отримати загальні вирази для середньої потужності поглинання довільною системою розподілів тиску в позначеннях: матриця повних провідностей відносного об’єму потоку, з метою застосування тиску для системи, вимушений об’єм потоку через набігаючий та розсіюваний потенціали, і (прийняті лінійними) характеристики тиск — об’єм потоку потужно-злетного механізму.

Далі показано, що під досягнутим імпедпнсом розуміють максимальну середню потужність поглинання можна визначити виключно, вирішуючи задачу лінійної хвильової дифракції, яка звичайна для корабельної гідродинамічної теорії без посилання до розподілів тиску. З нових результатів випливає, що необхідний коефіцієнт демпфування для даних розподілів тиску до вимушеного об’єму потоку виникає з задачі дифракції. Більшість цих результатів отримано в додатку.

У імовірнішому випадку недосконалої відповідності, показано, що для окремих розподілів тиску в двох або трьох вимірах, існують умови для резонансу, які додають розмір розподілу тиску до довжини набігаючої хвилі. Порівняння з резонансними умовами для твердих пристроїв хвильової енергії показує, що відбуваються тільки невеликі розходження при значеннях
ka
у межах практично необхідного діапазону, припускається, що використання таких твердих моделей пристроїв, які залежать від представлення поверхневого тиску для їх дії, забезпечить задовільні результати. Для більшого ka, однак, відбуваються істотні розходження, і це буде важливо в нелінійних задачах, де розглядаються високочастотні компоненти Фур’є. Взагалі, однак, в майбутньому може не виправдатись використання теорії твердого тіла краще ніж існуючої теорії для таких пристроїв, оскільки на додаток до більш точно опису фізичної ситуації, вона також має перевагу у створенні простіших задач з граничними значеннями, які необхідно вирішити.

Дана стаття тільки намагається відкрити теорію поглинання енергії розподілами тиску і зрозуміло, що виникає ряд задач, які необхідно вирішити. Найбільший недолік теорії – притуплення характеристик турбіни і кожного розподілу тиску. Насправді, це більш схоже на квадрати у формулі (Фрай та Джеферс 1979). Потрібно дослідити припущення про незжимаємість прикладеного об’єму повітря. І ці пункти були описані Фалькао та Сарменто (1980), і здається імовірним, що, використовуючи відповідні розклади ряду Фур’є, вони могли б бути включеними в існуючу загальну теорію.

Подальший напрямок вивчення повинен застосувати загальну теорію до типового пристрою Каймея, для того щоб отримати значення оптимальної ширини захвата і тисків камери. Можливо, суттєвішим було б затримати таке застосування, поки теорія не продовжена, щоб включити справжні нелінійні характеристики турбіни.

Автор бажає підтвердити численні корисні обговорення з доктором Томасом та містером Томасом, з Університету Брістоля, і також подякувати їм за допомогу в обчисленні представлених результатів. Ця робота формує частину із триваючої програми дослідження, підтриманої S.E.R.C. грант GR/B76720.

Додаток

Взаємні відношення, які включають розподіли тиску

Формула (2.14) пропонує, за аналогією з теорією для ряду твердих енергопоглинаючих тіл, відношення:

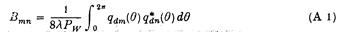
дотримується між елементами матриці демпфування B та елементами дифракційної хвилі викликаної вектором об’єму потоку qd. На додаток, в цьому додатку отримані подальші відношення до (А1), які відповідають вільно-поверхневим розподілам тиску. метод диференціювання витікає безпосередньо з використанням Ньюмана (1976), для того, щоб отримати відповідні результати для твердого тіла. В деякій мірі вони представлені тут, оскільки вони, здається, нові, і можуть мати застосування в інших контекстах, таких як вивчення транспортних засобів з повітряною подушкою.

Що стосується основної частини статті, потенціал y (x, y, z) задовольняє:

На більших відстанях y поводиться подібно потенціалу відбігаючої хвилі. Ми маємо:

не залежний від часу, складний об’єм потоку через Sі і з (2.11):

де

Нехай

де yj задовольняє (А2), (А3), (А6) і

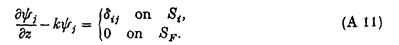
З (А7), (А8), (А10) витікає, що

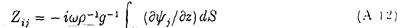
таким чином, щоб, зокрема:

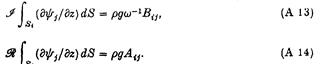
В результаті, припускаємо що:

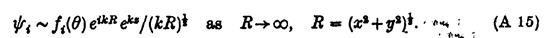
Дифракційний потенціал рівний:

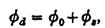
де

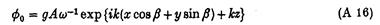
що задовольняє ¶fd/¶z = 0 на SB, фіксованих твердих поверхнях, і

Також

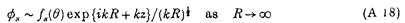
та ф0 і фS задовольняють (А5).

Тепер, якщо f і y — будь-які дві досить регулярні гармонічні функції в даній області:

де поверхневий інтеграл взятий над замкнутою поверхнею, яка включає область. Зокрема, розглянемо поверхневий інтеграл:

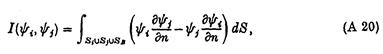
де інтегрування по і-й та j-й внутрішній вільній поверхні, а також по твердій границі SB. Тепер поверхня інтегрування (А20) може бути закрита більшим, вертикальним круглим циліндром Sc, який охоплює всі вільні поверхні та тверді границі і тягнеться від вільної поверхні вниз. Починаючи з y і , y j поведінка подібна убігаючій хвилі на більших відстанях, не дає додаткового внеску в (А20), отримується з інтегралу по Sc. Також, немає внеску від інтегралу по SF або по Sk, k = 1, …, N, k ¹і, k ¹ j. Отже з (А19) витікає, що:

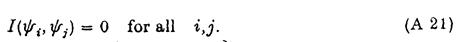
Снову внесок в (А20) від Su зникає на підставі умови (А3) і таким чином з (А20), (А11): показує що

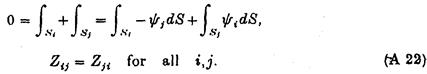
На цій стадії зручно, слідуючи Ньюману (1976), ввести функцію Коші:

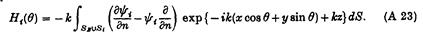
Оскільки y і та exp {- ik (x cosq + y sin q) + kz} — гармонічні функції, які задовольняють (А5), з (А19) витікає, що Hі(q) може бути записане як негативн величина того ж підінтегрального виразу проінтегрованого по Sc. Це дозволяє поведінку y і в далекій області, яка дана в (А15) використати для отримання:

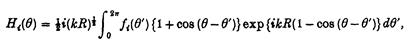
де

.

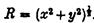Якщо, тепер R®¥, з методу стаціонарної фази випливає, що:

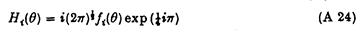
таким чином, що функція Коші безпосередньо пов’язана з розсіювальною амплітудою потенціалу y і в далекій області.

Тепер, прямою підстановкою:

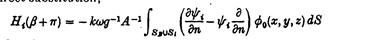
з ф0 дано (А16).

Ми можемо замінити ф0 — фd – фs. Але поверхневий інтеграл, який включає фs зникає, якщо, використовуючи (А19), ми заміняємо його негативним поверхневим інтегралом по Sj та Sc, ми знаходимо, що внеску від кожного y і та фs немає, і задовольняє умови (А5) і (А6).

Ми залишились з :

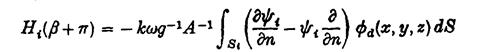
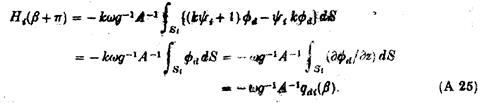
Маючи на увазі (А24), ми бачимо, що об’єм потоку через Sі через плюс дифрагованої області набігаючої хвилі пропорційний поведінці розсіяному потенціалу в далекій області в напрямку, протилежному до такої сукупності набігаючих хвиль, внаслідок однорідного коливального розподілу тиску через Sі. Цей результат відповідає відношенням Хакінда для руху твердих тіл (Ньюман 1976, рівняння (45).

Далі, ми розглядаємо:

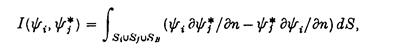
де * позначає сполучений комплекс. Оскільки y і , y*j задовольняють (А3) ми маємо:

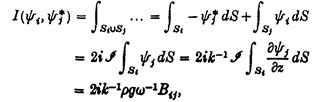
де використані (А11), (А13), (А22).

Знову: де використані (А15) і (А24).

Отже:

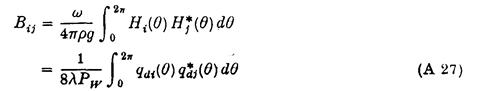
де використано (А25) і зроблена проста заміна змінної інтегрування. Тут

Pw=1/4w-1rg2A2 .

Окрім цих тривимірних результатів також можна отримати важливі двовимірні взаємовідношення для розподілів тиску. Рівняння (А2) — (А14) залишаються тими ж самими, але тепер (А15) потрібно замінити:

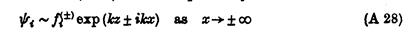
де рух відбувається в площині (x, z) . Подібно (А16) стає:

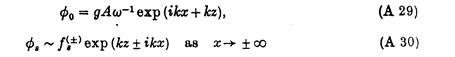
і функція Коші тепер визначена тільки для кутів b рівних 0 чи p. Попередній аргумент рухається маленькими кроками і результати в двовимірній області відповідають (А24), (А25), (А26) є:

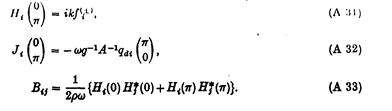
Рівняння для Hі (0) в (А32) відповідають набігаючій хвилі gАw-1 exp [- ikx + kz] з x=+¥, з qdі (p) , які відповідають об’єму потоку через Sі .

З (А31) і (А32) випливає, що:

Показує, що цьому у двовимірній області також вимушений потік через Sі за допомогою набігаючої та дифрагованої області пропорційний амплітуді випромінюваного потенціалу в далекій області в напрямку, в якому прибуває набігаюча хвиля. В (А34) qdi – об’єм потоку в одиниці ширини поверхневого тиску. Подальші відношення між властивостями рішення yі задачі потужності випромінювання та фd, рішенням дифракційної задачі в і дво- та тривимірних областях також можна отримати використанням функцій Коші та теореми Гріна. Зокрема, нові відношення, доведені Ньманом (1976), рівняння (48), (49)), переносяться на розподіли тиску без змін. Вони не подані тут, оскільки метод доведенняу ідентичний і вони не є необхідними в існуючому контексті.

З цього випливає, що всі результати, які зв’язують властивості вимушеного руху твердого тіла в даному способі (Ньюман 1976), або ряд незалежно коливающихся твердих тіл (Срокоз 1979), відповідають задачі дифракційного розсіювання області набігаючої хвилі таким тілом або тілами, мають аналогію в поверхневих розподілах тиску. Відповідність буде, якщо тверді тіла прийняті як тонкі горизонтальні пластини, які роблять одиничні вертикальні коливання у вільній поверхні. Хоча вимагається, щоб к дорівнювало нулю в (А11) у цьому випадку, це не торкається результатів, які отримані за допомогою теореми Гріна. Відповідність завершується відзначенням, що вертикальна захоплююча сила на Sі, тільки iwpk-1qdi, тобто пропорційна об’єму потоку через Sі.

Отримані деякі загальні результати для ефективності використання енергії системою однорідних осцилюючих поверхневих розподілів тиску. Результати, основані на класичній лінійній теорії водної хвилі, показують близькі аналогії з теоріями для систем поглинання коливальних твердих тіл, а також запропоновано і доведено безліч нових взаємовідношень для розподілів тиску. Деякі прості приклади, які ілюструють загальні результати даються у порівнянні з відповідними результатами для твердих тіл.