Учебная работа. Курсовая работа: Решение системы линейных алгебраических уравнений методом Крамера
Содержание
Введение
1. Создание С#
2. Постановка задачки
3. Способ Крамера
4. Программная реализации метода способа Крамера
Заключение
Перечень использованных источников
Введение
На практике почти всегда отыскать четкой решение появившейся математической задачки не удается. Это происходит основным образом не поэтому, что мы не умеем этого создать, а так как разыскиваемое решение обычно не выражается в обычных для нас простых либо остальных узнаваемых функциях. Потому огромное техники и с возникновением высокопроизводительных ЭВМ .
В истинной курсовой работе рассмотрена принципиальная, исходя из убеждений прикладных задач: способ Крамера для решение линейных алгебраических уравнений.
1. СОЗДЕНИЕ С #
Часто очень многого требований от инструментов, с которыми работаем, в особенности, когда это касается языков программирования. Хотя таковых языков существует величавое огромное количество, но лишь некие из их по-настоящему сильны. Эффективность языка заключается в его мощности и сразу — в гибкости. Синтаксис языка должен быть лаконичным, но ясным. Он должен содействовать созданию корректного кода и предоставлять настоящие способности, а не ультрамодные (и, обычно, тупиковые) решения. В конце концов, мощнейший язык обязан иметь одно нематериальное свойство: вызывать чувство гармонии. Как раз таковым языком программирования и является С#. Сделанный компанией Microsoft для поддержки среды .NET Framework, язык С# опирается на богатое наследство в области программирования. Его основным архитектором был ведущий спец в данной для нас области — Андерс Хейлсберг (Anders Hejlsberg).
С# -— прямой потомок 2-ух самых удачных в мире компьютерных языков: С и C++. От С он унаследовал синтаксис, главные слова и операторы. Он дозволяет выстроить и усовершенствовать объектную модель, определенную в C++. Не считая того, С# близко связан с иным весьма удачным языком: Java. Имея общее происхождение, но различаясь в почти всех принципиальных качествах, С# и Java — это быстрее «двоюродные братья». к примеру, они оба поддерживают программирование распределенных систем и оба употребляют промежный код для заслуги переносимости, но различаются при всем этом в деталях реализации. Делая упор на мощнейший фундамент, который составляют унаследованные свойства, С# содержит ряд принципиальных новшеств, поднимающих Искусство программирования на новейшую ступень. К примеру, в состав частей языка С# включены такие понятия, как делегаты (представители), характеристики, индексаторы и действия. Добавлен также синтаксис, который поддерживает атрибуты; облегчено создание компонент за счет исключения заморочек, связанных с COM (Component Object Model — модель компонентных объектов Microsoft — обычный механизм, включающий интерфейсы, при помощи которых объекты предоставляют свои службы иным объектам).
И еще. Подобно Java язык С# дает средства динамического обнаружения ошибок, обеспечения сохранности и управляемого выполнения программ. Но, в отличие от Java, C# дает программерам доступ к указателям. Таковым образом, С# соединяет первозданную мощь C++ с типовой сохранностью Java, которая обеспечивается наличием механизма контроля типов (type checking) и корректным внедрением шаблонных классов (template class). Наиболее того, язык С# различается тем, что соглашение меж мощью и надежностью кропотливо сбалансирован и фактически прозрачен (не приметен для юзера либо программки).
В протяжении всей истории развития вычислительной техники эволюция языков программирования означала изменение вычислительной среды, метода мышления программистов и самого подхода к программированию. язык С# не является исключением. В непрекращающемся процессе усовершенствования, адаптации и внедрения инноваций С# в истинное время находится на фронтальном крае. Это — язык, игнорировать существование которого не может ни один проф программер.
2. Постановка задачки
К решению систем линейных уравнений сводятся бессчетные практические задачки. Можно с полным основанием утверждать, что решение линейных систем является одной из самых всераспространенных и принципиальных задач вычислительной арифметики [1,2].
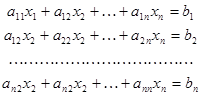 (1)
(1)
совокупа коэффициентов данной для нас системы запишем в виде таблицы:
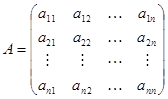
Запишем систему
линейных алгебраических уравнений с
неведомыми.
Данная таблица
2
частей, состоящая из
строк и
столбцов, именуется квадратной матрицей порядка
. Если схожая таблица содержит
частей, расположенных в
строчках и
столбцах, то она именуется прямоугольной матрицей.
Используя понятие матрицы
, систему уравнений (3) можно записать в векторно-матричном виде:
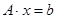
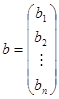 ,
,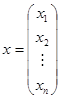
либо, в наиболее малогабаритной записи,
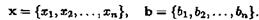
где
и
— вектор-столбец неведомых и вектор-столбец правых частей соответственно.
3. способ Крамера
метод Крамера, согласно [1,2], выражается формулами
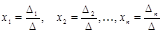
где 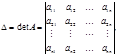
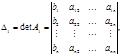
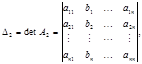 …,
…,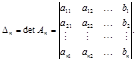
При всем этом нужным и достаточным условием существование единственного решения, является не равенство нулю головного определителя системы
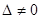 .
.
Блок-схема метода представлена на рисунке.
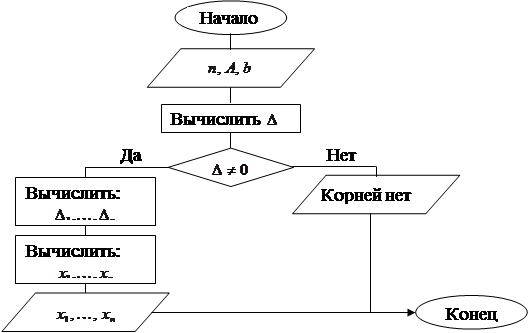
4. Программная реализации метода МЕТОДА КРАМЕРА
Главным способом класса Programm, является способ Main. С него начинается выполнение программки. В нашем случае, он содержит простой пользовательский интерфейс, по средством которого юзер вводит размерность системы, элементы матрицы системы
и вектора правых частей
(1, глава 1), а опосля нужных вычислений на дисплее возникает итог – элементы вектора
.
В работе, метод Крамера для большей читабельности, разбит на отдельные функции – способы:
staticdoubledet(intn, double [,]B) – способ вычисляющий определитель матрицы. Параметрами этого способа являются – количество уравнений (
), а так же матрица, в нашем случае
. Определитель матрицы рассчитывается непосдедственно, т.е. разложением по первой строке [3];
staticvoidequal(intn, double [,]A, double [,]B) – способ присваивающий матрицы (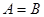 ), где
), где
-размерность матриц;
staticintSLAU_kramer(intn, double[,] A, double[] b, double[] x) – способ реализующий способ Крамера, согласно блок схеме главы 2.
В качестве языка программирования мы употребляли объектно – направленный язык С#. Наш выбор обоснован его гибкостью в разработке и разработке программых товаров [4-7].
текст программки приведет ниже.
usingSystem;
using System.Collections.Generic;
using System.Text;
namespace ConsoleApplication_Kramer
{
class Program
{
static void Main(string[] args)
{
int n; /* количество уравнений */
double [,] A = new double [3,3]; /* матрица системы */
double [] b = new double [3]; /* вектор правых частей */
double [] x = new double [3]; /* вектор решения */
char qq;
Console.Write(«Введите количество уравнений(<=3) n -> «);
n = Convert.ToInt32(Console.ReadLine());
if (n > 3 || n <= 1)
{
Console.WriteLine(«Ошибка в размерности системы (n=2,3)»);
Convert.ToInt32(Console.ReadLine());
return;
}
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
{
Console.Write(«A{0}{1} -> «,i,j);
A[i,j] = Convert.ToDouble(Console.ReadLine());
}
for(int i=0; i<n; i++)
{
Console.Write(«b{0} -> «, i);
b[i] = Convert.ToDouble(Console.ReadLine());
}
if(SLAU_kramer(n,A, b, x)==1)
{
Console.WriteLine(«Система не имеет решение»);
Convert.ToInt32(Console.ReadLine());
return;
}
else
for(int i=0; i<n; i++)
Console.WriteLine(«x»+i+» = «+x[i]);
Console.ReadLine();
}
private
static double det(int n, double [,]B)
{
if (n == 2)
return B[0,0] * B[1,1] — B[0,1] * B[1,0];
return B[0,0] * (B[1,1] * B[2,2] — B[1,2] * B[2,1]) — B[0,1] * (B[1,0] * B[2,2] — B[1,2] * B[2,0])+
B[0,2]*(B[1,0] * B[2,1] — B[1,1] * B[2,0]);
}
static void equal(int n, double [,]A, double [,]B)
{
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
A[i,j]=B[i,j];
}
static void change(int n, int N, double[,] A, double[] b)
{
for(int i=0; i<n; i++)
A[i,N]=b[i];
}
public
static int SLAU_kramer(int n, double[,] A, double[] b, double[] x)
{
double [,]An = new double [3,3];
double det1 = det(n, A);
if (det1 == 0) return 1;
for (int i = 0; i < n; i++)
{
equal(n, An, A);
change(n, i, An, b);
x[i] = det(n, An) / det1;
}
return 0;
}
}
}
программка, реализующая способ Крамера, была протестирована на последующий тестовых примерах.
Решить систему второго порядка
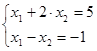
решением систены является вектор
 .
.
Итог выполнения программки представлен на рис. 1.
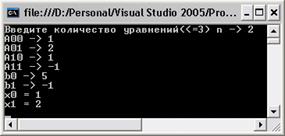
Рис. 1. Итог выполнения программки для системы второго порядка.
Решить систему третьего порядка
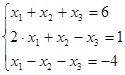
решением систены является вектор
 .
.
Итог выполнения программки представлен на рис. 2.
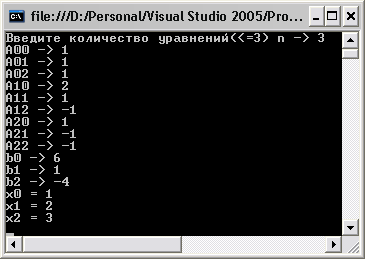
Рис. 2. Итог выполнения программки для системы третьего порядка.
В процессе тестированя, так же были рассмотрены случаи неверного ввода размерности, итог выполнения на рис.3 и вариант несовместности системы уравнений рис.4.
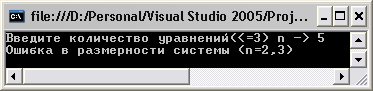
Рис. 3. Итог выполнения программки в слуае неверного ввода размерности системы.
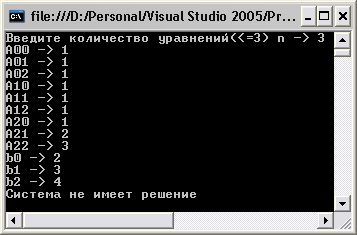
Рис. 4. Итог выполнения программки в случае несовместности системы.
Следует увидеть, что в программке не ошуществляется проверка корректность ввода частей матрицы и вектора правых частей.
ЗАКЛЮЧЕНИЕ
В работе, нами был программно реализован способ Крамера для решения системы линейных алгебраических уравнений. Мы употребляли нужное условие существования решения, т.е. не равенство нулю головного определителя системы.
Отличительная черта этого способа заключается в многократном вычислении определителя матрицы. С вычислительной точки зрения это трудозатратная операция с ростом количества частей. В работе была рассмотрена система 3-го порядка, а определители рассчитывались конкретно.
Но это не понижает Ценность работы, потому что переход к решению СЛАУ с неведомым количеством уравнений осуществляется конфигурацией способа, вычисляющий определитель матрицы.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Турчак Л.И. Базы численных способов / Л.И. Турчак, П.В. Плотников. — М.: ФИЗМАТЛИТ, 2002. — 304 с.
2. Демидович Б.П.Численные способы анализа / Б.П. Демидович, И.А. Марон,
Э.З. Шувалова. — М.: Наука, 1967.- 368 с.
3. Высшая математика для экономистов:Уч. Для вузов/Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман.-М.:Банки и биржи, 1998.-471 с.
4. Мохика Х. язык С#: разработка Web-приложений на ASP.NET / Х. Мохика; пер. с англ. А.А. Слинкина. – М.: НТ Пресс, 2006. – 464 с. – (QuickStart).
5. Либерти Дж. Программирование на C#: пер. с англ. / Дж. Либерти. – 2-е изд. – СПб.: знак, 2003. – 688 с.: ил.
6. С#: пер. с англ. / К. Ватсон, М. Беллиназо, О.Корнс и др. – СПб.: Питер, 2006. – 861 с.
7. Галисеев Г.В. Программирование на языке С#: самоучитель / Г.В. Галисеев. – М.: Вильямс, 2006. – 368 с.: ил.
]]>

