Учебная работа. Реферат: Основные цели, определения и принципы математического моделирования, виды моделей

Учебная работа. Реферат: Основные цели, определения и принципы математического моделирования, виды моделей

ПРЕДИСЛОВИЕ

Целью курса моделирование подъемно-транспортных систем является обучение основам моделирования подъемно-транспортных машин (ПТМ), что содержит в себе составление математических моделей ПТМ, программную реализацию моделей на ЭВМ , также получение, обработку и анализ результатов моделирования.

Для самостоятельного ознакомления с перечисленными вопросцами рекомендуется последующая литература: Брауде В. И., Тер-Мхитаров М. С. «Системные способы расчета грузоподъемных машин», Игнатьев Н. Б., Ильевский Б. З., Клауз Л. П. «Моделирование системы машин», Рачков Е. В., Силиков Ю. В. «Подъемно — транспортные машинки и механизмы», также справочники и учебные пособия по численным способам вычислительной арифметики и использованию математического редактора MathCad.

§1. ОСНОВНЫЕ ЦЕЛИ, определения И ПРИНЦИПЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ, ВИДЫ МОДЕЛЕЙ

1.1 Главные определения

Моделирование — это теоретико-экспериментальный способ познавательной деятель, это способ исследования и разъяснения явлений, действий и систем (объектов-оригиналов) на базе сотворения новейших объектов — моделей.

Моделирование – это замещение исследуемого объекта (оригинала) его условным образом либо остальным объектом (моделью) и исследование параметров оригинала методом исследования параметров модели.

Зависимо от метода реализации все модели можно поделить на 4 группы: физические, математические, предметно-математические и комбинированные [6, 19].

Физическая модель – реальное воплощение тех параметров оригинала, которые интересует исследователя. Физические модели именуют еще макетами, потому физическое моделирование именуется макетированием.

Математическая модель – это формализованное описание системы (либо процесса) при помощи некого абстрактного языка (математически), к примеру, в виде графов, уравнений, алгоритмов, математических соответствий и пр.

Предметно-математические модели являются аналоговыми, т.е. при всем этом для моделирования употребляется принцип схожего математического описания действий, настоящего и протекающего в модели.

Комбинированные модели представляют собой сочетание математической либо предметно-математической и физической модели. Они употребляются тогда, когда математическое описание 1-го из частей исследуемой системы непонятно либо проблемно, также по условиям моделирования нужно ввести в качестве элемента физическую модель (к примеру, тренажер).

Математическое моделирование – это замещение оригинала математической моделью и исследование параметров оригинала на данной модели.

Системой именуется объединение нескольких объектов (частей), взаимосвязанных меж собой, образующее определенную целостность.

Система владеет последующими, т.н. «системными» качествами:

1) структурой, т.е. строго определенным порядком объединения частей в группы;

2) целенаправленностью либо функциональностью, т.е. наличием цели, для которой сотворена система;

3) эффективностью, способностью достигать цели с меньшими затратами ресурсов;

4) устойчивостью, способностью сохранять свойства собственных параметров постоянными в определенных границах при изменении наружных критерий.

В истинное время в технике для исследования работы машинных комплексов и машин употребляется понятие «человеко-машинной системы» (ЧМС), т.е. смешанной системы, составной частью которой вместе с техническими объектами является человек-оператор [13, 20]. Не считая того, ЧМС ведет взаимодействие с окружающей средой. Таковым образом, для моделирования ПТС нужно разглядывать систему человек-Машинка-Среда, которая быть может отображена последующим графом (Рис. 1).

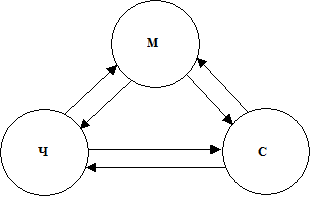
Рис. 1 Граф системы Человек-Машинка-Среда.

Стрелками на графе изображены потоки энергии, вещества и инфы, которыми обмениваются элементы системы.

Процессы, протекающие в технических системах, образованы совокупой простых операций. Операции – преобразования входных физических величин в выходные в низкоуровневом элементе системы (Рис. 2).

В любом элементе системы (Ei
) происходит преобразование входных действий (Xi
) в выходные (Yi
), при этом выходные действия 1-го элемента могут являться входными последующего. соединение частей в структурную схему по нраву передачи действий происходит поочередно либо параллельно.

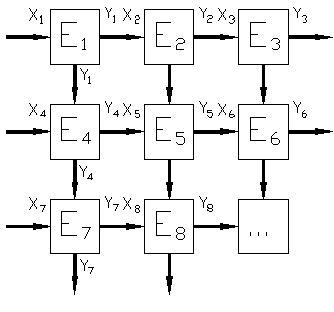
Рис.
2 Структурная схема системы.

Подъемно-транспортными системами (ПТС), изучаемыми в рамках данного курса, будем именовать системы, включающими в себя человека, окружающую среду и подъемно-транспортные машинки (ПТМ).

ПТМ – это машинки, созданные для перемещения груза на относительно маленькие расстояния без его переработки. ПТМ используются для облегчения, убыстрения, увеличения эффективности перегрузочных работ.

1.2 Принципы и виды математического моделирования

Математические модели должны владеть последующими качествами:

1) адекватность, свойство соответствия модели и объекта исследовательских работ;

2) достоверность, обеспечение данной вероятности попадания результатов моделирования в доверительный интервал,

3) точность, незначимое (в границах допустимой погрешности) расхождение результатов моделирования с показателями настоящих объектов (действий);

4) устойчивость, свойство соответствия малых конфигураций выходных характеристик малым изменениям входных;

5) эффективность, способность заслуги цели с малыми затратами ресурсов;

6) адаптабельность, способность просто перестраиваться для решения разных задач.

Для заслуги этих параметров есть некие принципы (правила) математического моделирования [17], ряд которых приведен ниже.

1) Принцип целенаправленности
состоит в том, что модель обязана обеспечивать достижение строго определенных целей и, сначала, отражать те характеристики оригинала, которые нужны для заслуги цели.

2) Принцип информационной достаточности
заключается в ограничении количества инфы о объекте при разработке его модели и поиске оптимума меж вводимой информацией и плодами моделирования. Он быть может проиллюстрирован последующей схемой.

1

2

3

наличие инфы

о объекте

Информация отсутствует стопроцентно

информация не полна

Доступна вся информация

Необходимость моделирования

Модель невозможна

Моделирование

Модель не нужна

Все вероятные случаи моделирования размещаются в столбце 2.

3) Принцип осуществимости
заключается в том, что модель обязана обеспечивать достижение поставленной цели с вероятностью близкой к 1 и за конечное время. Этот принцип можно выразить 2-мя критериями

и , (1)

где — возможность заслуги цели, — время заслуги цели, и — допустимые значения вероятности и времени заслуги цели.

4) Принцип агрегатирования
состоит в том, что модель обязана состоять из подсистем 1-го уровня, которые, в свою очередь, состоят из подсистем 2-го уровня и т.д. Подсистемы должны оформляться в виде отдельных самостоятельных блоков. Схожее построение модели дозволяет употреблять обычные процедуры расчетов, также делает наиболее легкой адаптацию модели к решению разных задач.

5) Принцип параметризации
состоит в подмене при моделировании определенных характеристик подсистем, обрисованных функциями, надлежащими числовыми чертами.

процесс моделирования с внедрением этих правил заключается в выполнении последующих 5 шагов (шагов).

1) Определение целей моделирования.

2) Разработка концептуальной модели (расчетной схемы).

3) Формализация.

4) Реализация модели.

5) анализ и интерпретация результатов моделирования.

Значительные различия в выполнении 3-5 шагов разрешают гласить о 2-ух подходах к построению модели.

Аналитическое моделирование
– это внедрение математической модели в виде дополненных системой ограничений уравнений, связывающих входные переменные с выходными параметрами. Аналитическое моделирование употребляется, если существует законченная постановка задачки на исследования и нужно получить один конечный итог, соответственный ей.

Имитационное моделирование
– это внедрение математической модели для описания функционирования системы во времени при разных сочетаниях характеристик системы и разных наружных действиях. Имитационное моделирование употребляется, если конечной постановки задачки не существует и нужно изучить протекающие в системе процессы. Имитационное моделирование подразумевает соблюдение временного масштаба. Т.е. действия на одели происходят через интервалы времени пропорциональные событиям на оригинале с неизменным коэффициентом пропорциональности.

По использованию средств для реализации модели можно выделить еще один вид моделирования, компьютерное моделирование. Компьютерное моделирование – это математическое моделирование с внедрением средств вычислительной техники.

1.3 Систематизация математических моделей

Все математические модели можно поделить на несколько групп по последующим классификационным признакам.

1) По виду моделируемой системы модели бывают статические и динамические. Статические модели служат для исследования статических систем, динамические для исследования динамических. Динамические системы характеризуются тем, что владеют обилием состояний, которые изменяют во времени.

2) По целям моделирования модели разделяются на нагрузочные, управленческие и многофункциональные. Нагрузочные модели служат для определения нагрузок, работающих на элементы системы, управленческие – для определения кинематических характеристик исследуемой системы, к которым относятся скорости и перемещения частей системы, многофункциональные – для определения координат модели в пространстве вероятных многофункциональных состояний системы.

3) По содержанию модели бывают детерминированные, стохастические и эвристические. характеристики детерминированных моделей определяются как неслучайные величины и функции, характеристики стохастических как случайные величины и функции, а эвристические модели в качестве 1-го из частей содержат в себе человека-оператора.

4) По степени дискретизации модели разделяются на дискретные, смешанные и континуальные. Дискретные модели содержат элементы, связанные меж собой, свойства которых сосредоточены в точках. Это могут быть массы, объемы, силовые и остальные действия, сосредоточенные в точках. Континуальные модели содержат элементы, характеристики которых распределены по длине, по площади либо по размеру всего элемента. Смешанные модели содержат элементы обоих типов.

§2 ОБЪЕКТЫ МОДЕЛИРОВАНИЯ

2.1 Система ЧМС

Итак, в качестве объекта моделирования выбрана система человек-ПТМ-окружающая среда.

Исследуя связи меж элементами ПТС (Рис. 3) целенаправлено выделить несколько типов связей, которые представляют энтузиазм исходя из убеждений моделирования ПТС. Это управляющие действия, информация, поступающая к оператору, действия окружающей среды на ПТМ.

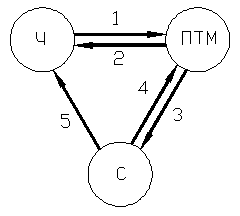
Рис.
3 ПТС.

1 — управляющие действия, 2 – действия работающей ПТМ на человека-оператора и информация, 3 – действия ПТМ на окружающую среду, 4 – наружные действия среды на ПТМ, 5 – действия окружающей среды на человека-оператора и информация.

Разглядим верхушки графа по отдельности.

Более сложна, исходя из убеждений моделирования, задачка моделирования деятель человека-оператора
. Исследование роли человека оператора осуществляется способами инженерной психологии. Некие вопросцы инженерной психологии можно отыскать в работах [6] и [35]. Для моделирования работы ПТМ нужно задать управляющие действия оператора. Задание управляющих действий в модели осуществляется последующими методами:

1) математической обработкой экспериментальных данных (массивы черт управляющих действий за некий просвет работы ПТМ);

2) включением человека-оператора в модель;

3) математическими зависимостями, выражающими связь меж управляющими действиями, чертами оператора и действиями на него, приобретенные методом обработки статистической инфы о эксплуатации данного типа машин.

В окружающей среде
можно выделить две составляющих: технологическую и природную.

Технологическая среда представляет собой специально организованные условия, нужные для выполнения ПТМ собственных функций.

В действиях природной среды можно выделить энерго и информационные. В первую группу входят силовые, кинематические, температурные, радиационные и био действия. Кинематические действия – это конфигурации кинематических связей, накладываемых средой на ПТМ. К температурным относятся действия температуры воздуха, к радиационным – действие солнечной радиации, к биологическим – действия биосферы на ПТМ: грибковые образования, деяния насекомых, звериных и птиц. Главный Энтузиазм в рамках курса представляют силовые действия, посреди которых можно выделить последующие типы:

— гравитационные, перегрузки от веса частей машинки и груза;

— ветровые, перегрузки, вызванные давлением ветра на элементы ПТМ;

— перегрузки от снега и обледенения;

— перегрузки, вызванные качкой (для плавучих ПТМ);

— экстремальные, перегрузки, вызванные экстремальными ситуациями: землетрясениями, наводнениями, ударами и т.д.

информация может поступать конкретно к оператору (зрительная, акустическая) либо, опосредованно, через приборы и датчики ПТМ.

Номенклатура ПТМ
очень многообразна [1, 7, 16, 30, 34]. Они разделяются по способу деяния на два огромных класса:

— грузоподъемные машинки (ГПМ), машинки повторяющегося деяния, в каких происходит последовательное повторение движений частей машинки для перемещения груза, называемое циклом;

— машинки непрерывного транспорта (МНТ), ПТМ, обеспечивающие непрерывное перемещение грузов без остановки машинки для их захвата и выгрузки.

Крайние могут работать в автоматическом и автоматическом режиме, что существенно упрощает моделирование управляющих действий.

По способу сотворения движущей силы МНТ бывают механическими, установками трубопроводного транспорта и гравитационными – спускными самотечными устройствами.

По типу движения ГПМ разделяются на три группы:

— перемещающие груз в вертикальном и горизонтальном направлении (краны и перегружатели);

— перемещающие груз в вертикальном либо близком к нему направлении (подъемники: лифты и вагоноопрокидыватели);

— перемещающие груз в горизонтальном либо близком к нему наклонном направлении (погрузчики и т.д.).

2.2 свойства объектов моделирования.

Для моделирования ПТС нужно избрать и задать те свойства ЧМС, которые разрешают найти состояние исследуемого элемента зависимо от входных действий в хоть какой момент времени.

На рисунке 4 представлена структурная схема модели, где знаками обозначены

X
— вектор входных действий,

Y
— вектор выходных действий,

S
— вектор, черт состояния системы (элемента).

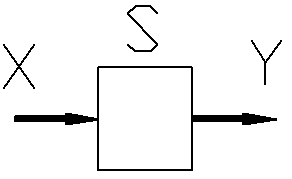
Рис.
4 Структурная схема модели.

Высококачественный состав векторов определяется целями моделирования, посреди которых можно выделить последующие:

1) определение хороших характеристик системы,

2) установление связей меж входными и выходными параметрами системы,

3) исследование действий, протекающих в системе при разных свойствах входных действий и моделируемых ситуациях,

4) тренировка.

Опосля определения целей нужно составить концептуальную модель либо расчетную схему. Ее составление включает последующие этапы.

1) Сбор и анализ инфы о системе:

а) сбор фактических данных и выдвижение гипотез о тех параметрах, данные о которых неопознаны либо не достоверны,

б) выбор учитываемых характеристик объекта моделирования в согласовании с целями моделирования,

в) выбор типа модели в согласовании с целями моделирования.

2) Декомпозиция системы:

а) разбиение системы на огромное количество подэлементов,

б) установление связей меж элементами системы,

в) математическое описание установленных связей.

Опосля разбиения ЧМС на элементы первого (высшего) уровня, мы получим три составляющих (человек-оператор, среда, ПТМ), которые в свою очередь являются сложными системами. Разглядим их по отдельности.

2.3 человек-оператор, как объект моделирования

Человек-оператор (ЧО), исходя из убеждений математического моделирования, представляет собой более непростой объект. Если представить ЧО как систему, имеющую вход и выход (Рис. 4), то высококачественный состав векторов для моделирования, будет смотреться последующим образом:

X
– входные действия,

X1

– информационные действия,

X1.1

– информационные действия от ПТМ (информация о положении частей ПТМ, показания устройств и т.д.),

X1.2

– информационные действия окружающей среды,

X1.3

– стратегическая управляющая информация,

X2

– энерго действия,

X2.1

– энерго действия ПТМ на ЧО,

X2.2

– энерго действия окружающей среды на ЧО,

Y
– выходные действия,

Y
1
– управляющие действия (моменты включений/выключений устройств, положения переключателей либо моменты начала действий, длительность и интенсивность действий),

S
– свойства объекта моделирования,

S1

– квалификация,

S2

– личные свойства оператора.

Исходя из убеждений моделирования и конструирования ПТМ, больший Энтузиазм представляют управляющие действия. Управляющие действия представляют собой набор импульсов, характеризующих работу соответственных устройств ПТМ: включение механизма в одном направлении, в оборотном направлении и отключение данного механизма / торможение механизма. Обычно, процесс управления состоит из временами циклической группы операций.

[34]

Главный чертой цикла является время цикла.

При разных технологических вариантах перегрузки и разных родах груза время, затрачиваемое на отдельные операции, будет различно, а, означает, и время цикла будет различным. С временем цикла тесновато соединено понятие производительности машинки. Производительность машинки является принципиальной чертой ее свойства.

[34]

Техно производительность определяется по формуле

, (2)

где
– вес груза, т, nц


— число циклов, выполняемых машинкой за час,
ц
– средняя длительность цикла для данных критерий, с. Число циклов определяется по формуле

. (3)

Для роста производительности машинки нужно очень уменьшить время цикла либо прирастить грузоподъемность. время цикла зависит от деятельности ЧО либо выдачи им управляющих действий. Также деятельность ЧО влияет на процессы, протекающие в элементах машинки, на окружающую среду и т.д. Потому, при моделировании ПТС, нужно учесть деятельность ЧО.

Деятельность ЧО как функционирование хоть какой кибернетической системы быть может сведена к восприятию инфы, ее переработке и использованию для управления машинкой [35]. Моделирование выдачи управляющих действий оператором может осуществляться последующими 3-мя методами: включением человека в модель, математическим описанием процесса выдачи действий и комбинированным методом, заключающимся в использовании статистических обработок настоящего процесса управления. При использовании второго метода нужно выстроить зависимости меж параметрами управляющих действий и действиями на ЧО с учетом черт объекта. В управлении можно выделить две стадии. На первой стадии происходит выработка стратегии управления, на 2-ой реализация данной стратегии.

[27]

Мерой эффективности, избранной стратегии, служит
, показатель эффективности. Он отражает итог воплощения стратегии и является функцией 3-х характеристик: положительного эффекта (
), издержек ресурсов (
) и затраченного на выполнение операций времени (
). Значения
,
и
зависят от
, избранной стратегии, и
, вероятных ошибок при осуществлении данной стратегии. Т.е., показатель эффективности можно записать (4)

. (
4)

Зависимо от целей проведения операций параметрами
,
и
могут становиться разные свойства системы либо процесса. Также, при определенных критериях, некие аргументы могут быть опущены.

Как правило, выбор хорошей стратегии связан в управлении ПТМ с меньшими затратами времени на достижение цели, а другие составляющие входят в условие выбора хорошей стратегии в качестве доп ограничений

, (5)

где и — допустимые значения соответственных величин.

Таковым образом, будем считать главным вариантом лучшую стратегию, а отличия избранных стратегий управления от хорошей учесть при помощи соответственных коэффициентов (Kоткл

), зависящих от технологических вариантов перегрузки, рода груза и квалификации крановщика и определяемых по результатам тестов.

На стадии реализации избранной стратегии возникает суммарная ошибка, вызванная неправильной зрительной оценкой координат объекта и замедлением реакции ЧО. Так, оценка расстояния меж объектами по высоте в трехмерном пространстве происходит с ошибкой, равной 0,1-0,2 определяемой величины. время реакции на изменение скорости находится в оборотной зависимости от величины ее конфигурации. Величины ошибок также определяются экспериментально и нормируются зависимо от технологических вариантов перегрузки, рода груза и квалификации крановщика.

В согласовании с избранной стратегией с учетом вероятных ошибок при ее осуществлении делается выдача ЧО управляющих действий. Управляющие действия являются случайными событиями, которые характеризуются временем действия (моментами начала и конца действия) и величиной (уровнем) действия. Эти свойства являются случайными величинами.

Случайная величина – величина, которая может принять какое-либо неведомое заблаговременно
[8]

Главной вероятностной чертой случайной величины является законраспределения.

законраспределения быть может представлен в виде ряда распределения, функции распределения и плотности распределения.

Таблица, в какой перечислены все вероятные значения случайной величины и надлежащие им вероятности именуется распределения.

x1

x2

x3

xN

p1

p2

p3

pN

Возможность того, что случайная величина воспримет x
, является функцией, зависящей от
, и именуется функцией распределения либо интегральным законом распределения.

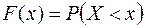
Функция распределения является всепригодным законом распределения, т.к. существует и для дискретных, и для непрерывных случайных величин.

Производная от функции распределения охарактеризовывает плотность распределения вероятности по случайной величине и именуется плотностью распределения вероятности либо дифференциальным законом.

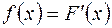
Главными числовыми чертами случайной величины являются математическое ожидание (МО), дисперсия и среднеквадратическое отклонение (СКО).

МО охарактеризовывает положение случайной величины на числовой оси и определяется как и для дискретных и непрерывных величин соответственно.

Дисперсия охарактеризовывает рассеяние случайной величины около МО, является квадратом отличия случайной величины от ее МО и определяется как и для дискретных и непрерывных величин соответственно.

СКО определяется как квадратный корень из дисперсии и служит для большей наглядности рассеяния величины.

Ошибки управления зависят от огромного количества случайных причин. При равном воздействии огромного количества случайных причин на величину можно гласить о
ее распределения [11]. Плотность распределения крайнего описывается формулой

, (6)

где — МО и СКО случайной величины, соответственно.

Наружный вид обычной плотности распределения представлен на рис. 5.

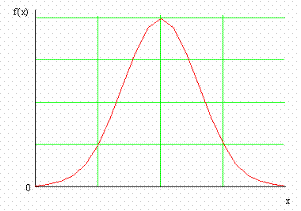
Рис.
5 Обычный законраспределения.

Управляющие действия представляют собой вектора, владеющие последующим набором черт

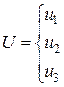
где u1

– время начала действия, u2

– время конца действия, u3

– величина (уровень) действия. Эти свойства — случайные величины, распределение которых также подчинено нормальному закону. МО величин являются их значения в точности надлежащие избранной стратегии. СКО соединены с отклонениями от избранной стратегии многофункциональной зависимостью. Отличия от избранной стратегии представляют собой суммарные ошибки оператора, вызванные задержкой реакции, рассогласованием, неверной информацией о положении рабочих органов ПТМ и груза. Они нормируются зависимо от квалификации оператора.

разряд

I

II

III

…

величина ошибки

…

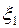
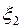
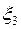
При моделировании свойства управляющих действий определяются или с учетом распределения их вероятности, или по зависимости

, (7)

Для получения достоверных и четких результатов нужно употреблять стохастическую модель. Данные, приобретенные при помощи машинных тестов, обрабатываются способами математической статистики [10].

Пусть есть величина
умеренно распределенная на интервале [0,1]. Для преобразования умеренно распределенных случайных чисел в числа, распределенные по нормальному закону, воспользуемся преобразованием

, (8)

где — МО величины, — СКО величины.

2.4 объект моделирования – окружающая среда

Окружающая среда повлияет на ЧО и ПТМ. Эти действия учитываются обилием

, в каком Y1

– действия на ЧО, действующие, в главном, на его способность принимать информацию и выдавать управляющие действия, Y2

– действия на ПТМ, складывающиеся из действий, меняющих характеристики материалов, из которых сделаны элементы ПТМ, действий, меняющих свойства частей ПТМ и нагрузок. Зависимо от локального климата района, сейсмической активности и т.д. выделяют несколько зон [32, 33]. Каждой зоне соответствуют свои характеристики действий на ПТМ, которые случайны. Главный Энтузиазм представляют силовые действия окружающей среды на ПТМ.

1) Ветровые перегрузки являются распределенными по наветренной площади перегрузками, действующими горизонтально и включающими статическую и динамическую составляющие.

Наветренной площадью именуется Рис.
6 Наветренная площадь

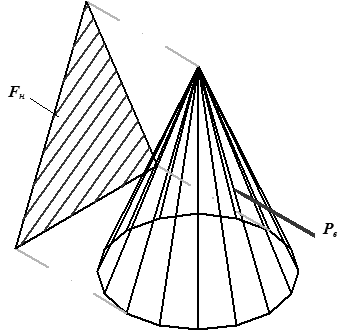
Ветровую нагрузку можно разглядывать как сосредоточенную силу, приложенную в центре масс наветренной площади. Положение центра масс сечения (площади) определяется по известным зависимостям

, , (9)

и при переходе к предельным значениям

() , , (10)

где
— площадь сечения,
и
– координаты по оси абсцисс и оси ординат, соответственно (Рис. 7).

Исходя из этих зависимостей, находим координаты центра масс сечения наветренной площади.

Статическая составляющая ветровой перегрузки определяется по формуле

, (11)

где — наветренная площадь, — коэффициент, учитывающий изменение динамического давления по высоте, — коэффициент аэродинамической силы, учитывающий аэро форму элемента, — динамическое давление (высокоскоростной напор) ветра, принимаемое зависимо от вида расчета (рабочее/нерабочее состояние) и района установки ПТМ.

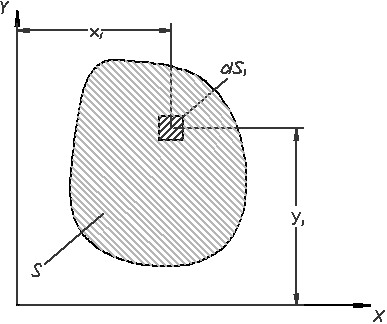
Рис.
7 Поперечное сечение элемента

Учет динамической составляющей ветровой перегрузки делается при помощи динамического коэффициента, зависимо от расчетного варианта он принимается равным kд

=1.4-1.6.

2) Перегрузки от снега и обледенения – это перегрузки, распределенные по горизонтальной площади ПТМ и ее частей, действующие вертикально вниз (вес снега и льда). Величины их определяются как произведение данной площади на давление снега и льда, равное 500-2500 Па зависимо от района установки ПТМ. Точкой (точками) приложения перегрузки (нагрузок) является центр (центры) тяжести сечения горизонтальных проекций площадей ПТМ и ее частей.

3) В районах, подверженных землетрясениям, учитываются горизонтальные сейсмические силы, прикладывающиеся к центру масс ПТМ

, (12)

где — сейсмический коэффициент, принимаемый зависимо от сейсмической балльности района, — вес ПТМ, кН.

4) Гравитационные действия – это силы тяжести груза и частей ПТМ, направленные вертикально вниз и распределенные по размеру элемента. Сила тяжести груза – случайная величина, возможность возникновения которой распределена по некому закону, почаще всего близкому к нормальному. Силы тяжести частей также являются случайными величинами и изменяются в границах 5% от собственной величины. Они подчиняются нормальному закону распределения. При моделировании могут заменяться сосредоточенными перегрузками, приложенными в центрах масс частей. Они определяются по зависимости , где
i

– масса
-го элемента ПТМ,
– убыстрение вольного падения.

Также при моделировании могут учитываться технологические перегрузки, связанные с выполнением ПТМ технологических операций, и особенные перегрузки, вызванные недостатками производства, ошибками управления, редчайшими природными явлениями либо Деятельностью людей, впрямую не связанной с данной машинкой.

2.5 объект моделирования – ПТМ

ПТМ – система, состоящая из огромного количества частей. Это огромное количество можно разбить на четыре группы. К ним относятся элементы металлоконструкции, приводы либо механизмы, электрооборудование и прочее и вспомогательное оборудование (Рис. 8). В свою очередь, приобретенные группы содержат подгруппы, состоящие из подгрупп наиболее низкого уровня, и т.д. Степень детализации зависит от целей разраба.

Рис.
8 Структурная схема ПТМ (мостового крана)

Элементы металлоконструкции ПТМ – это балки, фермы, колонны. Они владеют объемом и массой, которая распределяется по размеру элемента по некому закону (Рис. 9).

Рис.
9 Металлоконструкции ПТМ.

Но почаще всего они рассматриваются как стержневые системы, масса которых быть может как распределена по длине, так и сосредоточена в нескольких точках либо точке, как правило, центре тяжести элемента. При всем этом инерционными чертами частей модели являются приведенная масса либо приведенный момент инерции. Приведение крайних делается на основании равенства кинетических энергий настоящего элемента и элемента с приведенной массой и осуществляется по последующим зависимостям

либо , (13)

где mi

и Ji

– инерционные свойства частей конструкции, и – скорости движения частей конструкции в поступательном и вращательном движении, соответственно, и — скорости движения элемента с приведенной массой в поступательном и вращательном движении, соответственно.

Также элементы металлоконструкции владеют упругостью, т.е. способностью восстанавливать форму опосля снятия перегрузки, вызвавшей изменение формы элемента. Настоящие элементы металлоконструкции владеют линейной упругостью по осям X, Y, Z и изгибной либо крутильной упругостью в плоскостях XOY, XOZ, YOZ. Упругость частей металлоконструкции характеризуется коэффициентом жесткости, угловым либо линейным, зависимо от вида деформации. Как правило, при моделировании учитывается тот тип упругости элемента, который соответствует большей его деформации. При подмене оригинала элементом модели крайний характеризуется коэффициентом жесткости, определенным на основании равенства возможных энергий настоящего и моделируемого объектов по зависимостям

либо , (14)

где ci

и – жесткостные свойства частей конструкции, xi

и – деформации частей конструкции в поступательном и вращательном движении, соответственно,
пр

и — деформации элемента с приведенным коэффициентом жесткости в поступательном и вращательном движении, соответственно.

При работе ПТМ элементы ее металлоконструкции совершают сложное пространственное движение. Учет упругости частей не считая переносного и относительного движения частей конструкции, соответственных выполнению главных рабочих движений, подразумевает рассмотрение упругих колебаний, возникающих в элементах конструкции из-за взаимодействия сил упругости и сил инерции.

Разглядим, например, портальный кран (Рис. 10).

Рис.
10 Портальные перегрузочные краны.

Работая, кран совершает последующие движения: поворот, подъем/опускание груза и изменение вылета. Также может быть перемещение крана вдоль штабеля груза по крановым путям. Для роста рабочей площади, которую может обработать кран, используются т.н. стрелы с рабочим конфигурацией вылета. Качание стрелы происходит в интервале от малого до наибольшего вылета. При всем этом обрабатываемая краном площадь возрастает, но центры тяжести стреловой системы и груза поднимаются на некую величину, что просит доп издержек энергии. Уменьшение либо исключение этих издержек достигается с помощью уравновешивания веса груза и собственного веса стрелового устройства. Для уравновешивания веса груза употребляются особые устройства, называющиеся уравновешенными стрелами. Уравновешивание веса груза состоит в обеспечении близкой к горизонтали линии движения перемещения груза при изменении вылета стрелы. Для что употребляются четырехзвенные стреловые системы, именуемые шарнирно-сочлененные устройства (ШСУ). ШСУ бывают с прямым и профилированным хоботами, с гибкой и твердой оттяжками. ШСУ с прямым хоботом и твердой оттяжкой (рис. 10) представляет собой шарнирный четырехзвенник Чебышева, созданный для преобразования вращательного движения входного звена в поступательное выходного. На большей части собственной линии движения конец выходного звена четырехзвенника {перемещается} по пологой кривой полосы, близкой к горизонтали. Выполнение краном рабочих движений приводит к возникновению раскачивания груза на канатах в плоскости вылета и из плоскости вылета стрелы. Если ограничиться плоскостью вылета и не учесть упругость частей стреловой системы, ее можно представить последующей расчетной схемой (рис. 11), где настоящие элементы металлоконструкции изменены двухопорными опорами с сосредоточенными в центрах тяжести частей массами.

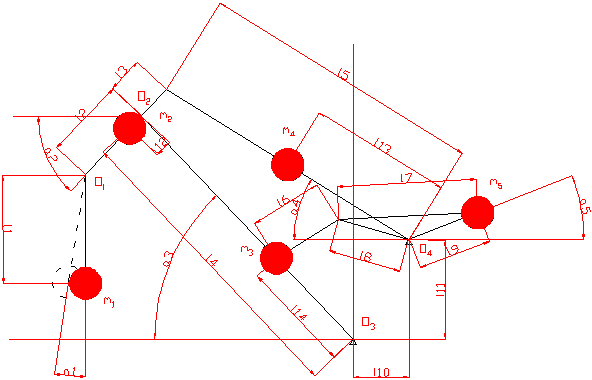
Рис.
11 Схема стреловой системы.

На схеме представлены главные элементы стреловой системы: хобот, стрела, оттяжка, противовес, соединенный со стрелой тягой, и груз, подвешенный на канатах. На схеме обозначены:

— длина канатной подвески, размеры

и

— хобота,

— стрелы,

— оттяжки,

— тяги противовеса,

,

и

-противовеса,

и

— положение точки крепления оттяжки,

,

,

,

и

— массы груза, хобота, стрелы, оттяжки и противовеса, соответственно,

,

и

— положения центров масс хобота, оттяжки и стрелы, соответственно. При изменении вылета происходит вращение перечисленных частей около шарниров, обозначенных знаками
с индексами. Так как модель твердая, т.е. все элементы полностью твердые, то положения всех частей, а, означает, и их скорости являются функциями вылета (скорости конфигурации вылета) либо угла наклона стрелы (скорости конфигурации угла наклона стрелы).

Таковым образом, при составлении расчетной схемы для твердой модели стреловой системы нет необходимости разглядывать все элементы ШСУ по отдельности и можно ограничиться двухмассовой расчетной схемой с 2-мя обобщенными координатами (Рис. 12).

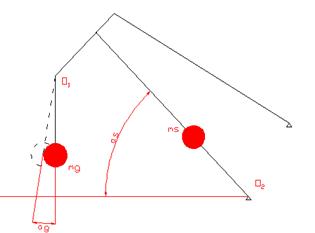
Рис.
12 Схема стреловой системы

На схеме обозначены последующие обобщенные координаты модели:
— угол отличия грузовых канатов от вертикали,
— угол наклона стрелы к горизонтали; приведенные массы:
— масса груза и грузозахватного устройства,
— приведенная к точке крепления тяги масса частей стрелового устройства.

Массу

найдем по зависимости (13). движение масс системы, изображенной на схеме (Рис. 11), является сложным. Для записи выражения для кинетической энергии целенаправлено пользоваться последующим методом. Поначалу определим декартовы координаты масс системы, приняв за начало координат в любом случае более комфортную точку. Потом, дифференцируя по времени приобретенные координаты, найдем проекции скоростей масс на оси координат и, дальше, квадраты абсолютных скоростей масс.

1) Для массы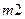

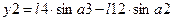
Для массы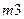

Для массы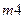

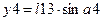
Для массы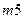

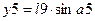
2)

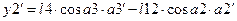
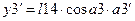
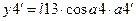
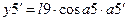
3)

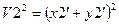
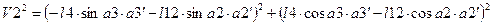
либо упрощая

.

2-ое слагаемое выражения охарактеризовывает кинетическую энергию массы при качании относительно точки , оставшиеся относительно точки и т.д.

Тогда выражение для кинетической энергии масс системы можно записать в виде

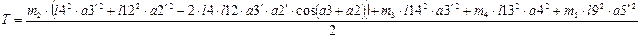
а для приведенной массы

, где . Отсюда найдем приведенную массу.

В тех вариантах, когда при моделировании нужно учитывать колебательные процессы, протекающие в элементах металлоконструкции, количество степеней свободы и обобщенных координат, также дискретных масс значительно возрастает.

Рис.
13 Виды стержней.

В вариантах сложного движения () нужно учесть

действия приводов складываются из действий движков и тормозов устройств.

При моделировании допускается действия тормозов устройств разглядывать в виде прямоугольных импульсов, т.е. считаем, что момент тормоза прикладывается одномоментно и по величине равен нормативному значению.

действия устройств задаются при помощи механических черт движков с учетом передаточного дела механизма.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Моделирование. определения, виды моделирования.

2. Модель. Определения, виды моделей.

3. Математические модели. определения, виды математических моделей.

4. Системы, характеристики систем, структура системы.

5. Человеко-машинные системы (ЧМС), подъемно-транспортные машинки (ПТМ), подъемно-транспортные системы (ПТС).

6. Принципы математического моделирования.

7. Характеристики математических моделей.

8. Последовательность шагов математического моделирования.

9. Мировозренческая модель (схема).

10. Среда, как объект моделирования. Виды действий среды на ПТМ и человека-оператора (ЧО).

11. Человек-оператор, как объект моделирования. Виды действий ЧО на ПТМ и окружающую среду.

12. методы учета ЧО при выдаче управляющих действий.

13. ПТМ, как объект моделирования.

14. Цели моделирования.

15. Этапы составления концептуальной модели.

16. методы моделирования процесса воплощения управляющих действий.

17. Лучшая стратегия управления. методы выбора хорошей стратегии.

18. Случайное событие, случайная величина, свойства случайной величины.

19. Моделирование силовых действий окружающей среды на элементы ПТМ.

20. Моделирование действий приводов ПТМ.

21. структура системы ПТМ.

22. Характеристики частей металлоконструкции ПТМ, учитывающиеся при моделировании.

23. характеристики частей приводов ПТМ, учитывающиеся при моделировании.

24. структура привода ПТМ.

25. Индивидуальности разных типов приводов ПТМ.

26. Декомпозиция системы при составлении концептуальной модели.

27. Методы представления частей металлоконструкции ПТМ при составлении расчетной схемы.

28. Пример составления расчетной схемы для твердой модели мостовой телеги.

29. Пример составления расчетной схемы для упругой модели мостовой телеги.

30. методы задания модельного времени.

31. Методы составления моделей и типы моделей зависимо от вида инфы о моделируемом объекте.

32. Регрессионные модели.

33. Планируемый факторный причин.

35. Границы применимости модели.

36. Способы оценки степени воздействия количественных причин на отклик.

37. Способы оценки степени воздействия высококачественных причин на отклик.

38. Характеристики матрицы планирования и определение коэффициентов регрессии.

39. способ меньших квадратов.

40. Проверка адекватности модели.

ЛИТЕРАТУРА

1. Александров М.П. Подъемно-транспортные машинки. — М.: Высшая школа, 1985. 520 с.

2. Артоболевский И. И. Теория машин и устройств. — М.: Наука, 1988. 638 с.

3. Бать М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и задачках. В 2-х т. Т. 1. М.: Наука, 1966. 632 с.

4. Бать М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и задачках. В 2-х т. Т. 2. М.: Наука, 1966. 664 с.

5. Бидерман В. Л. Теория механических колебаний. — М.: Высшая школа, 1980. 480 с.

6. Брауде В.И., Тер-Мхитаров М.С. Системные способы расчета

грузоподъемных машин. — Л.: Машиностроение, 1985.
181 с.

7. Вайнсон А.А. Подъемно — транспортные машинки. — М.: Машиностроение, 1989. 431 с.

8. Вентцель Е.С. Теория вероятностей. — М.: Наука, 1962.
576 с.

9. Вибрации в технике: Справочник: В 6-ти т. Т. 6 / Под ред. К. В. Фролова. – М.: Машиностроение, 1995. 456 с.

10. Гмурман В.Е. Теория вероятностей и математическая статистика. — М.: Высш. школа, 1977. 479 с.

11. Гнеденко Б.В. Курс теории вероятностей. — М.: Наука, 1988.
448 с.

12. Головачев П.А., Гладунко Ю.И. Техно эксплуатация и установка подъемно — транспортных машин. — М.: Транспорт, 1985.
304 с.

13. ГОСТ 26387-84 Система «человек-машина». Определения и определения.

14. Гохберг М.М. Железные конструкции подъемно — транспортных машин. — Л.: Машиностроение, 1976. 450 с.

15. Григорьев Н.И. Перегрузки кранов. — М. — Л.: Машиностроение, 1964.
168 с.

16. Грузоподъемные машинки / М.П. Александров, Л.Н. Колобов, Н.А. Лобов и др. — М.: Машиностроение, 1986.
395 с.

17. Гультяев А. К.
MATLAB 5.2. Имитационное моделирование в среде Windows: Практическое пособие. – СПб.: КОРОНА принт, 1999. – 288 с.

18. Дьяконов В.П. Справочник по методам и программкам на языке Бейсик для индивидуальных ЭВМ . — М.: Наука, 1989. 240 с.

19. Игнатьев Н. Б., Ильевский Б. З., Клауз Л. П. Моделирование системы машин. – Л.: Машиностроение, 1986. 423 с.

20. Информационно-управляющие человеко-машинные системы: Исследование, проектирование, испытание: Справочник / А. А. Адаменко, А. Т. Ашеров и др. — М.: Машиностроение, 1993. 494 с.

21. Комаров М. С. Динамика грузоподъемных машин. — М.: Машгиз, 1962.
267 с.

22. Корн Г., Корн Т. Справочник по арифметике для научных работников и инженеров. — М.: Наука, 1984.
832 с.

23. Лобов Н. А. Динамика грузоподъемных кранов. — М.: Машиностроение, 1987.
376 с.

24. Математический энциклопедический словарь. / Гл. ред. Ю. В. Прохоров. — М.: Русская энциклопедия, 1988. 847 с.

25. Мостеллер Ф., Тьюки Дж. анализ данных и регрессия. — М.: Деньги и статистика, 1982. 319 с.

26. Налимов В. В. Теория опыта – М.: Наука, 1971. 207 с.

27. Научно-технический прогресс. / Словарь. – М.: Политиздат, 1987. 366 с.

28. Павлов Н. Г. Примеры расчетов кранов. — Л.: Машиностроение, 1976. 320 с.

29. Правила устройства и неопасной эксплуатации грузоподъемных кранов. — СПб.: Издательтво ДЕАН, 2004. — 272 с.

30. Рачков Е. В., Силиков Ю. В. Подъемно — тра

нспортные машинки и механизмы. — М.: Транспорт, 1989. 240 с.

31. Себер Дж. Линейный регрессионный анализ. — М.: Мир, 1980. 456 с.

32. Справочник по кранам / в 2 т. Т. 1; Под общ. ред. М. М. Гохберга. — Л.: Машиностроение, 1988. 536 с.

33. Справочник по кранам / в 2 т. Т. 2; Под общ. ред. М. М. Гохберга. — Л.: Машиностроение, 1988.
559 с.

34. Шерле З. П. Каракулин Г. Г. Справочник механизатора речного порта. – М.: Транспорт, 1980. 391 с.

35. Тер-Мхитаров М.С. Оператор перегрузочных машин. – Пермь: Кн. изд-во, 1982. – 140 с.

]]>