Учебная работа. Лабораторная работа: Разложение в ряды Тейлора
Нижегородский муниципальный институт
имени Н.И. Лобачевского
Факультет ВМК
Разложение в ряды Тейлора
отчет по дисциплине:
Информатика и программирование
Выполнила:
Студентка
(в/о)
Проверила:
Нижний Новгород
2006
Содержание
1.
Введение……………………………………………………….. стр. 3
2.
Постановка задачки………………………………………………………. стр. 5
3.
Управление юзера…………………………………………… стр. 6
4.
Управление программера………………………………………….. стр. 7
5.
Заключение…………………………………………………………………. стр. 8
6.
Перечень литературы …………………………………………………….. стр. 10
7.
приложение……………………………………………………………….. стр. 11
Введение
Ряд Тейлора – степенной ряд вида:
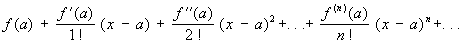
, (1)
где
(
) — функция, имеющая при
=
производные всех порядков. В почти всех фактически принципиальных вариантах этот ряд сходится к
(
) на неком интервале с центром в точке а:
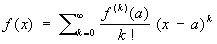
(2)
(эта формула размещена в 1715 Б. Тейлором)
Разность Rn
(
) =
(
) — Sn
(
)
где Sn
(
) — сумма первых
+ 1 членов ряда (1), именуется остаточным членом Т. р. Формула (2) справедлива, если 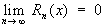
. Т. р. можно представить в виде
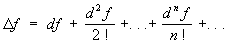
,
применимом и к функциям почти всех переменных.
При
= 0 разложение функции в Т. р. воспринимает вид:
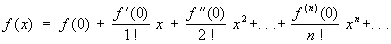
,
а именно:
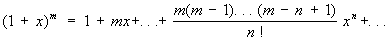
(3)
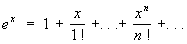
(4)
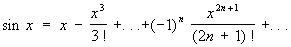
(5)
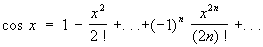
(6)
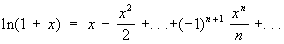
.(7)
Ряд (3), являющийся обобщением на вариант дробных и отрицательных характеристик формулы двучлена Ньютона, сходится: при -1<
< 1, если
< -1; при -1< x £ 1, если -1<
< 0; при -1 £ x £ 1, если
> 0
Ряды (4), (5) и (6) сходятся при всех значениях
ряд (7) сходится при -1< x £ 1.
Функция
(
) всеохватывающего переменного
постоянная в точке
раскладывается в Т. р. по степеням
—
снутри круга с центром в точке я и с радиусом, равным расстоянию от
до наиблежайшей особенной точки функции
(
)
Вне этого круга Т. р. расползается, Постановка задачки
Задачка состоит в том, чтоб посчитать через ряд Тейлора функцию и сопоставить её
Предлагается разглядеть три функции: sin, cos и exp.
Для каждой из их существует разложение в ряд Тейлора.
Разложения:
1. 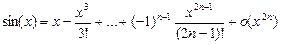
2. 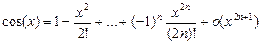
3. 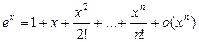
Нескончаемо малыми пренебрежем.
Управление юзера
1. Запускаем программку.
На дисплее возникает основное меню:
1 – sin x
2 – cos x
3 – exp x
4 – Выход
2. Избираем функцию: синус, косинус либо экспонент.
3. Вводим аргумент.
4. Вводим количество слагаемых.
5. Получаем итог и точность в вычислении.
Примечание

Основное меню
Управление программера
В программке употребляются переменные процедурного типа.
Поточнее, мы присваиваем переменной функцию, проверяем правильность данного параметра и позже при помощи переменной процедурного типа вычисляем пошагово в цикле очередной член ряда и прибавляем его к сумме.
В программке функциям передаются последующие характеристики: аргумент, точность вычислений (число членов ряда) и переменная процедурного типа, указывающая на функцию, которая возвращает новейший член ряда. Функции вычисляют новейший член ряда на базе аргумента и номера члена. В функции не передаётся предшествующий член ряда, так как итог выполнения этих функций домножается на предшествующий член ряда.
Заключение
При большенном количестве членов ряда (начиная с 10-14 для различных рядов) погрешность в вычислениях становится так мала, что время от времени округляется до нуля. При стремлении числа слагаемых в бесконечность погрешность стремится к нулю. В итоге мы получаем корректный итог при большем количестве членов ряда.
В итоге данной работы была написана программка и были проведены эксперементы, плодами которых явилось:
1.
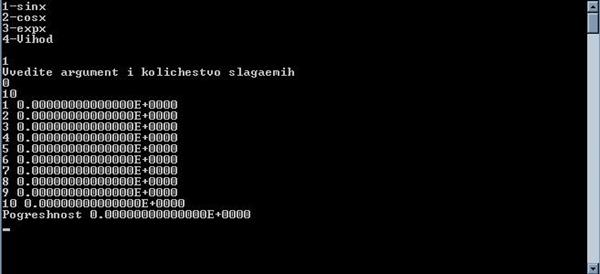
Sin x
2.
Cos x
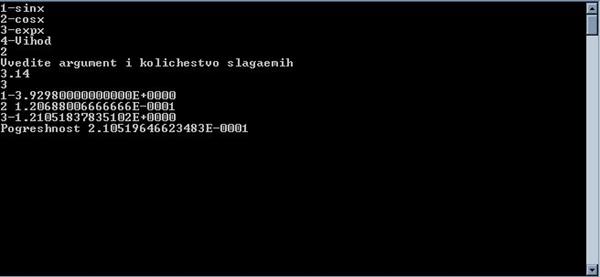
3.
Exp
X
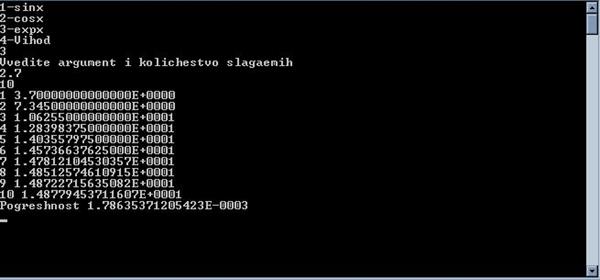
Перечень литературы
1. Л.Д. Кудрявцев «Курс математического анализа»
2. В.Г. Абрамов, Н.П. Трифонов, Г.Н. Трифонова «Введение в язык Паскаль».
Приложение
program teylor;
uses
SysUtils;
var a,x,sum: real;
n,i,answ: integer;
begin
writeln (‘Viberite funkciyu’);
writeln (‘1-sinx’);
writeln (‘2-cosx’);
writeln (‘3-expx’);
writeln (‘4-Vihod’);
readln (answ);
writeln (‘Vvedite argument i kolichestvo slagaemih’);
readln (x,n);
case answ of
1: begin
a:=x;
sum:=a;
for i:=1 to n do
begin
a:=a*(-1)*x*x/(2*i*(2*i+1));
sum:=sum+a;
writeln (i, sum);
end;
writeln (‘Pogreshnost’, абс(sin(x)-sum));
end;
2: begin
a:=1;
sum:=1;
for i:=1 to n do
begin
a:=a*(-1)*x*x/((2*i)*(2*i-1));
sum:=sum+a;
writeln (i, sum);
end;
writeln (‘Pogreshnost’, абс(cos(x)-sum));
end;
3: begin
a:=1;
sum:=1;
for i:=1 to n do
begin
a:=a*x/i;
sum:=sum+a;
writeln (i, sum);
end;
writeln (‘Pogreshnost’, абс(exp(x)-sum));
end;
end{case};
readln;
end.
]]>

