Учебная работа. Курсовая работа: Построение математических моделей методом идентификации
2-ая часть работы – численные процедуры оценивания характеристик нелинейных регрессионных моделей. По-заданию требуется воплотить один из численных способов поиска МНК-оценок.
3-я часть работы содержит в себе разработку аналитической модели хим реактора безупречного смешения. Не считая разработки модели нужно выполнить линеаризацию способами идентификации, также построение кривых отклика линеаризованной и аналитической моделей.
Содержание
Реферат
Содержание
Задание 1. идентификация объектов способом меньших квадратов
Задание 2. Связь разных форм моделей динамических систем
Задание 3. Построение модели с распределенными параметрами
Задание 4 численные процедуры оценивания характеристик нелинейных регрессионных моделей
Задание 5 разработка аналитических моделей объектов автоматизации. Линеаризация моделей
Заключение
Задание 1. идентификация объектов способом меньших квадратов
1.1 Постановка задачки
Математическая модель объекта имеет вид:
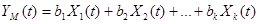 .(1.1)
.(1.1)
Имеются статистические данные наблюдений:
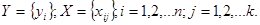
Известна диагональная корреляционная матрица ошибок наблюдений
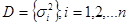 .
.
Требуется:
1. Оценить вектор коэффициентов модели В способом меньших квадратов.
2. Оценить вектор коэффициентов модели взвешенным способом меньших квадратов, считая точность измерения входных характеристик назад пропорциональной номеру показателя.
3. Оценить вектор коэффициентов модели способом наибольшего правдоподобия.
4. Выстроить доверительные интервалы для коэффициентов модели для доверительной вероятности 0,95.
5. Проверить значимость приобретенной статистической модели объекта.
6. Проанализировать приобретенные результаты.
Таблица 1.1
Вариант задания
Вариант
Матрица XT
Матрица YT
След матрицы D
5

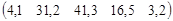
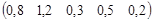
1.2 Математическая постановка задачки
Пусть имеются транспонированные матрицы результатов наблюдений и след диагональной корреляционной матрицы ошибок D:

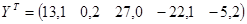
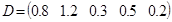
Так как результаты наблюдений сущность случайные величины, получить «настоящие» значения коэффициентов 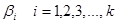 из модели
из модели
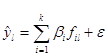 ;(1.2)
;(1.2)
недозволено. Заместо этого можно получить их оценки 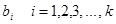 на базе исследовательских работ по таблице за ранее составленных наблюдений. Если речь идет о модели (1.2), то она воспринимает вид
на базе исследовательских работ по таблице за ранее составленных наблюдений. Если речь идет о модели (1.2), то она воспринимает вид
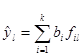 ,(1.3)
,(1.3)
где 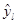 ─ предсказанное . Величина отклика служит оценкой «настоящего» значения
─ предсказанное . Величина отклика служит оценкой «настоящего» значения 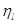 . В регрессионном анализе для получения оценок коэффициентов модели (1.2) употребляется МНК.
. В регрессионном анализе для получения оценок коэффициентов модели (1.2) употребляется МНК.
Из-за деяния случайных возмущений предсказанное будет различаться от результата измерения 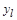 . Разности
. Разности 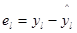 ,
, 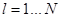 , именуют остатками.
, именуют остатками.
Потому что настоящее
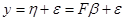 , а
, а 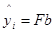 .
.
Отсюда вектор остатков:
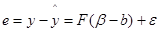 .
.
Оценки коэффициентов регрессии естественно находить так, чтоб обеспечить меньшие вероятные остатки, но остатки многочисленны, потому нужна некая суммарная черта, которая обязана зависеть от различий меж измеренными и предсказанными значениями выходных черт в любом опыте. Такую функцию обычно именуют функцией утрат, либо функцией риска. Для разных целей и критерий исследования она может иметь различный вид.
Вот одна из более нередко применяемых функций утрат:
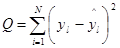 .(1.4)
.(1.4)
В ней остатки возведены в квадрат, чтоб восполнить различия в их знаках.
Запишем сумму (1.4) в векторной форме. Пусть
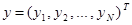
обозначает N-мерный вектор столбец измеренных значений отклика, а
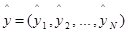
N-мерный вектор соответственных им предсказанных значений, в конце концов,
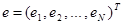
вектор-столбец остатков. Как понятно, скалярное произведение вектора на самого себя равно сумме квадратов его частей, потому выражении (1.4) можно переписать в виде
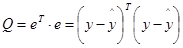 .(1.5)
.(1.5)
способ, позволяющий оценивать регрессионные коэффициенты, выбирают так, чтоб минимизировать величину Q. Его именуют обычно способом меньших квадратов.
Пусть на базе данных таблицы исследования необходимо отыскать такие оценки коэффициентов регрессии, которые минимизируют сумму Q, определенную в (1.4), минимум получим, приравняв производные по неведомым оценкам 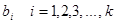 к нулю. Но поначалу подставим (1.2) в (1.4):
к нулю. Но поначалу подставим (1.2) в (1.4):
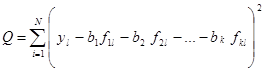 .(1.6)
.(1.6)
Опосля дифференцирования этого выражения по разыскиваемым оценкам и приравнивания нулю первых производных получаем систему уравнений:
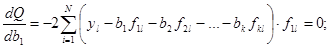
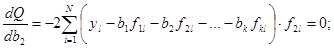 (1.7)
(1.7)
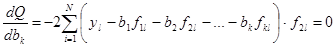 .
.
Константы -2
, входящие во все уравнения, не играют роли, ибо для равенства нулю произведения довольно, чтоб равными нулю оказались надлежащие суммы. Потому приобретенная система сводится к виду:
 (1.8)
(1.8)
Приобретенная система линейна относительно разыскиваемых оценок 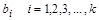 , а число уравнений в ней равно числу неведомых коэффициентов k модели. Она именуется системой обычных уравнений.
, а число уравнений в ней равно числу неведомых коэффициентов k модели. Она именуется системой обычных уравнений.
Запись системы обычных уравнений можно упростить, если положить
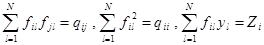 .(1.9)
.(1.9)
Разумеется 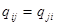 , так как порядок перемножения функций под знаком суммы не важен. В новейших обозначениях система обычных уравнений воспримет вид:
, так как порядок перемножения функций под знаком суммы не важен. В новейших обозначениях система обычных уравнений воспримет вид:
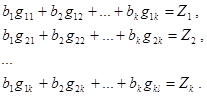 (1.10)
(1.10)
В предстоящем мы воспользуемся матричной записью. Обозначим 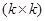 ─ матрицу величин
─ матрицу величин 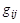 буковкой G,
буковкой G, 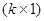 ─ вектор оценок разыскиваемых коэффициентов буковкой b,
─ вектор оценок разыскиваемых коэффициентов буковкой b, 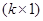 ─ вектор правой части системы буковкой Z. Тогда
─ вектор правой части системы буковкой Z. Тогда

Принципиально увидеть, что G ─ симметричная матрица, потому что 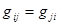 .
.
Вот матричная запись системы обычных уравнений:
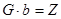 .(1.11)
.(1.11)
Матрица G именуется информационной матрицей
. Ее можно представить через введенную в матрицу (1.2.2) матрицу регрессоров 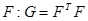 . Это утверждение проверяется конкретно транспонированием F и перемножением
. Это утверждение проверяется конкретно транспонированием F и перемножением 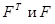 . Буквально так же проверяется, что
. Буквально так же проверяется, что 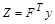 . означает, систему обычных уравнений можно переписать так:
. означает, систему обычных уравнений можно переписать так:
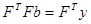 .(1.12)
.(1.12)
Если ранг F равен k, то ранг 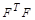 то же равенk, потому что из теории матриц понятно, что произведение матриц
то же равенk, потому что из теории матриц понятно, что произведение матриц 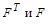 есть положительно определенная матрица.
есть положительно определенная матрица.
При этих критериях можно получить матрицу, оборотную к информационной. Обозначим ее 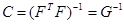 . Так как
. Так как 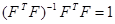 , умножение выражения (1.12) слева на матрицу
, умножение выражения (1.12) слева на матрицу 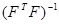 приводит к решению системы обычных уравнений:
приводит к решению системы обычных уравнений:
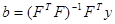 .(1.13)
.(1.13)
Таковым образом, решив матричное уравнение (1.13), мы получаем в векторе b
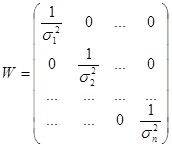
В случае неравноточных измерений значений входных величин применяется взвешенный способ меньших квадратов. Данный способ различается тем, что в матричное уравнение добавляется так именуемая матрица весов. Матрица весов представляет собой диагональную матрицу, элементами которой являются величины, назад пропорциональные квадрату дисперсии измерений входных величин:
Для взвешенного способа меньших квадратов матричное уравнение имеет вид:
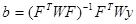 .(1.14)
.(1.14)
Для приобретенных коэффициентов регрессии доверительный интервал определяется таковым образом:
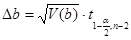 ,(1.15)
,(1.15)
где V(b) – дисперсия коэффициентов, 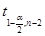 — коэффициент Стьюдента. Коэффициент Стьюдента определяется по таблицам. Для нашего варианта он равен 2,5. Дисперсия коэффициентов определяется по последующей формуле:
— коэффициент Стьюдента. Коэффициент Стьюдента определяется по таблицам. Для нашего варианта он равен 2,5. Дисперсия коэффициентов определяется по последующей формуле:
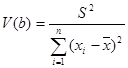 ,(1.16)
,(1.16)
где S – дисперсия оценки. Определяется последующим образом:
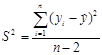 ,(1.17)
,(1.17)
Таковым образом получим значения коэффициентов регрессии в виде
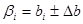 .
.
1.3 Результаты выполнения задания
способ меньших квадратов
Y=
D=
W=DT
=
1
1
1
4,1
0,8
1,25
-2
2
5
31,2
1,2
0,83
X=
5
-2
3
41,3
0,3
3,33
2
-1
1
16,5
0,5
2,00
3
2
1
3,2
0,2
5,00
Решение без диагональной корреляционной матрицы
1
-2
5
2
3
XT
=
1
2
-2
-1
2
1
5
3
1
1
43
-9
11
XT
X=
-9
14
6
11
6
37
0,032
0,027
-0,014
(XT
X)-1
=
0,027
0,099
-0,024
-0,014
-0,024
0,035
190,8
XT
Y=
-26,2
303,7
1,24
B=(XT
X)-1
XT
Y=
-4,77
8,61
y^
y
y^-y
(y^-y)2
5,08
4,1
0,98
0,962
31,06
31,2
-0,14
0,019
Проверка
41,56
41,3
0,26
0,066
15,85
16,5
-0,65
0,417
2,78
3,2
-0,42
0,174
Сумма
1,639
Решение с диагональной корреляционной матрицой
1,25
1,25
1,25
5,13
-1,67
1,67
4,17
26,00
WX=
16,67
-6,67
10,00
WY=
137,67
4,00
-2,00
2,00
33,00
15,00
10,00
5,00
16,00
1
-2
5
2
3
XT
=
1
2
-2
-1
2
1
5
3
1
1
140,92
-9,42
61,92
XT
WX=
-9,42
39,92
-2,42
61,92
-2,42
59,08
0,013
0,002
-0,014
(XT
WX)-1
=
0,002
0,026
-0,001
-0,014
-0,001
0,031
755,46
XT
WY=
-219,21
597,13
1,28
B=(XT
WX)-1
XT
WY=
-4,67
8,57
y^
y
y^-y
(y^-y)2
5,18
4,1
1,08
1,175
30,95
31,2
-0,25
0,063
41,47
41,3
0,17
0,028
15,81
16,5
-0,69
0,480
3,08
3,2
-0,12
0,014
Сумма
1,761
Расчет доверительных интервалов
1
1
1
y
y^-y
(y^-y)2
-2
2
5
4,1
0,465
0,216
X=
5
-2
3
31,2
-0,546
0,298
2
-1
1
41,3
-0,252
0,063
3
2
1
16,5
-0,119
0,014
3,2
0,371
0,138
Сумма
0,729
Хср=
1,8
0,4
2,2
b1=
1,235
b2=
-4,769
-0,8
0,6
-1,2
b3=
8,614
-3,8
1,6
2,8
Х-Хср=
3,2
-2,4
0,8
0,2
-1,4
-1,2
1,2
1,6
-1,2
1
1
1
4
4
25
Х2
=
25
4
9
4
1
1
9
4
1
Сумма
43
14
37
0,64
0,36
1,44
14,44
2,56
7,84
(X-Хcp)2
=
10,24
5,76
0,64
0,04
1,96
1,44
1,44
2,56
1,44
Сумма
26,8
13,2
12,8
S2
=
0,243
V(b1)=
0,078
V(b2)=
0,052
V(b3)=
0,141
b1
0,537
b2
-5,337
b3
7,677
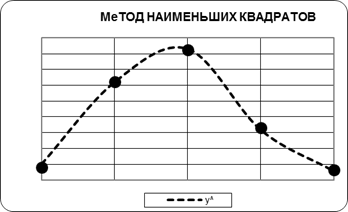
способ меньших квадратов рис 1.1

МНК график остатков рис 1.2
Задание 2. Связь разных форм моделей динамических систем
2.1 Постановка задачки
объект описан дифференциальным уравнением:
Требуется:
1. Записать модель объекта в пространстве состояний.
2. Записать модель объекта в форме передаточной функции.
3. Получить частотные свойства объекта.
2.2 Математическая постановка задачки
Разглядим систему автоматического управления (САУ), описываемую линейным (линеаризованным) дифференциальным уравнением вида:
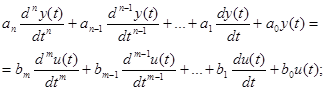 (2.1)
(2.1)
где u(t) – входной процесс, y(t) – выходной процесс, ai
, bj
– неизменные коэффициенты, n, m (n>m)– неизменные числа. В операторной форме выражение (2.1) быть может записано  .
.
тут D – оператор дифференцирования  . Отсюда преобразование “вход-выход” системы:
. Отсюда преобразование “вход-выход” системы:
где W(D) именуется операторной передаточной функции.
один из методов моделирования систем заключается в представлении преобразования “вход-выход” в виде всеохватывающей передаточной функции:
которая выходит методом внедрения преобразования Лапласа к (2.2) ри исходных нулевых критериях. тут s-комплексная переменная. Связь меж операторной (2.2) и всеохватывающей (2.3) передаточными функциями можно записать в виде:
Всеохватывающие числа, являющиеся корнями многочленаВ(s), именуются нулями передаточной функции, а корешки многочлена A(s) – полюсами.
Очевидный вид связи входа и выхода определяется выражением:
где w(t) – оригинал (т.е. приобретенный при помощи оборотного преобразования Лапласа) всеохватывающей передаточной функции W(s).
Динамические характеристики систем охарактеризовывают реакции на входные действия специального вида. А именно анализ выхода системы на единичный скачок и d-функцию (дельта-функцию).
Пусть u(t) = 1(t), другими словами на вход системы подается функция Хевисайда (единичный скачок), определяемая:
График функции Хевисайда приведен на рис. 2.1а:
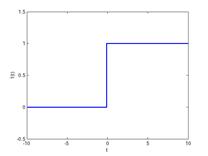 а)
а)
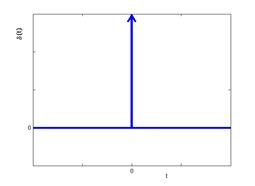 б)
б)
Рис.2.1. Функции Хевисайда (а) и Дирака (б)
Реакция САУ на единичный скачек именуется переходной функцией системы и обозначается h(t).
Если u(t) = d(t), другими словами на вход системы поступает функция Дирака (d-функция, импульсная функция, рис. 2.1б) определяемая:
то реакция САУ именуется импульсной переходной функцией системы и обозначается w(t). Таковым образом оригинал всеохватывающей передаточной функции можно измерить как реакцию систему на импульс.
Импульсная и переходная функции системы соединены соотношением:
Благодаря широкому применению при исследовании стойкости динамических систем и проектировании регуляторов получили распространение частотные свойства.
Пусть на вход системы с передаточной функцией W(s) подается гармонический сигнал u(t) = au
cos(wt), t>0. В этих критериях справедлива последующая аксиома:
Если звено является устойчивым, то установившаяся реакция y(t) на гармоническое действие является функцией той же частоты с амплитудой ay
= au
|W(iw)| и относительным сдвигом по фазе y = argW(iw).
Таковым образом, выход определяется гармонической функцией
y(t) = au
|W(iw)| cos(w t + argW(iw)),(2.9)
где i – всеохватывающая единица, 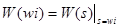 – частотная черта.
– частотная черта.
При фиксированном значении w частотная черта является всеохватывающим числом, и, как следует, быть может представлена в виде:
где  – амплитудно-частотная черта (АЧХ); – фазово-частотная черта (ФЧХ); – вещественная частотная черта (ВЧХ); – надуманная частотная черта (МЧХ).
– амплитудно-частотная черта (АЧХ); – фазово-частотная черта (ФЧХ); – вещественная частотная черта (ВЧХ); – надуманная частотная черта (МЧХ).
Геометрическое пространство точек W(iw) на всеохватывающей плоскости при изменении w от w0
до от w1
(обычно w0
= 0, w1
=  ), именуется амплитудно-фазовой чертой (АФХ) либо частотным годографом Найквиста.
), именуется амплитудно-фазовой чертой (АФХ) либо частотным годографом Найквиста.
Имеет обширное практическое
2.3 Результаты выполнения задания
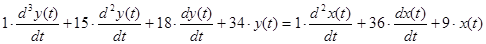
Исполняем анализ при помощи пакета прикладных программ MatLab
Передаточная функция имеет вид:
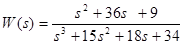
Полюса передаточной функции:
-13.8796
-0.5602 + 1.4614i
-0.5602 — 1.4614i
Нули передаточной функции:
-35.7482
-0.2518
С помощью команды step(w) строим переходную функцию h(t) рис2.2
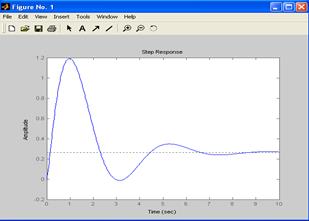
Рис.2.2. Переходная функция h(t)
С помощью команды impulse(w) строитьсяимпульсная переходная функция w(t) рис2.3:
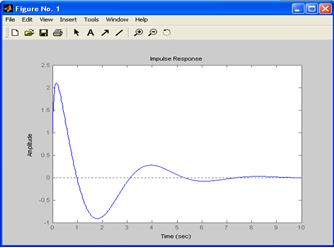
Рис. 2.3. Импульсная переходная функцияw(t)
С помощью команды bode(w) строим Диаграмму Боде рис 2.4:
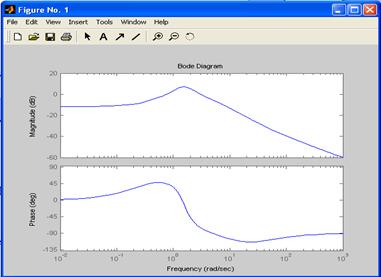
Рис.2.4. Диаграмма Боде
АФХ системы он жегодограф НайквистаW(iw), строится с помощью команды nyquist(w):
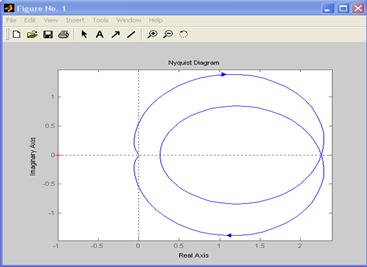
Рис. 2.5. Годограф Найквиста
текст расчетов в MatLab
>> w= TF([1,36,9],[1,15,18,34])
Transfer function:
s^2 + 36 s + 9
————————
s^3 + 15 s^2 + 18 s + 34
>>pole(w)
ans =
-13.8796
-0.5602 + 1.4614i
-0.5602 — 1.4614i
>>zero(w)
ans =
-35.7482
-0.2518
>>step(w)
>>impulse(w)
>>bode(w)
>>nyquist(w)
>>ltiview(w)
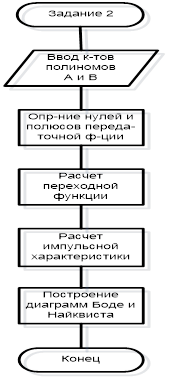
Набросок 2.6 – Блок-схема программки исследования черт динамической системы
Задание 3. Построение модели с распределенными параметрами
3.1 Постановка задачки
Применение способа конечных разностей для расчета термического режима жесткой стены
Плоская стена сначало прогрета умеренно до температуры 600С. В предстоящем на внутренней поверхности стены (х = 0) обеспечивается условие термоизоляции (плотность термического потока равна нулю), а с внешной поверхности (х = L) идет термообмен с наружной средой, имеющей постоянную температуру Тср = -40 0С.. Изменение температуры в стене осуществляется в итоге процесса теплопроводимости. Требуется получить зависимость от времени температуры на внутренней поверхности стены. Толщина стены L=20смб коэффициент теплоотдачи α=100Вт/м2К (неявная схема).
3.2 Математическая постановка задачки
Для неявной разностной схемы апроксимация уравнения теплопроводимости будет иметь последующий вид:
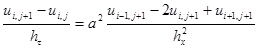 (3.1)
(3.1)
сейчас комфортно ввести 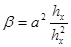 и в левой и правой части сгруппировать все члены с индексрмj+1:
и в левой и правой части сгруппировать все члены с индексрмj+1:
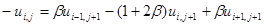 (3.2)
(3.2)
Популярная функция u(i,j) связана многофункциональной зависимостью с 3-мя неведомыми функциями на следующем слое. Для данного временного слоя такие уравнения нужно записать для всех внутренних точек i=2….n-1 и дополнить их граничными критериями i=1,n. Тогда получим систему с 3-х диагональной матриц неведомых членов, которая решается при помощи способа прогонки.
Потому что в задачке заданна температура окружающей среды, то имеем граничные условия 3-го рода. Запишем уравнения для граничных и внутренних точек 1-го временного слоя.
Для i=1, имеем:
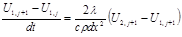 (3.3)
(3.3)
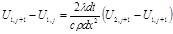 (3.4)
(3.4)
Обозначим  ,
, 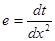 , получим уравнение для i=1:
, получим уравнение для i=1:
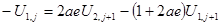 (3.5)
(3.5)
Для i=2…n-1, имеем:
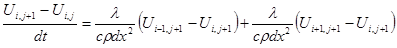 (3.6)
(3.6)
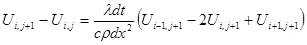 (3.7)
(3.7)
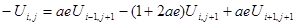 (3.8)
(3.8)
Для i=n, имеем:
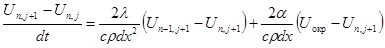 (3.9)
(3.9)
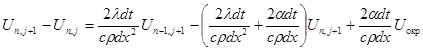 (3.10)
(3.10)
Обозначим 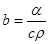 ,
, 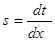 , получим уравнение для n=1:
, получим уравнение для n=1:
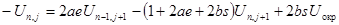 (3.11)
(3.11)
Разглядим способ прогонки для решения системы, сотоящей из уравнений (3.5), (3.8), (3.11). Из уравнения (3.5) выразим U1,
j
+1
:
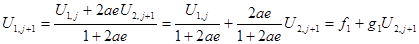 (3.12)
(3.12)
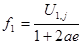 ,
, 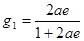 (3.13)
(3.13)
Запишем уравнение для i=2 (3.8) и подставим в него выражение (3.12) и выразим U2,
j
+1
:
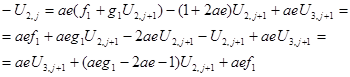 (3.14)
(3.14)
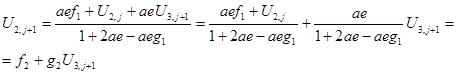 (3.15)
(3.15)
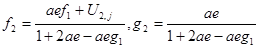 (3.16)
(3.16)
Продолжим этот процесс до i=n-1, получим:
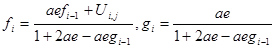 (3.17)
(3.17)
Коэффициенты fi
и gi
известны из граничных критерий на первой границе f1
=U1,
j
и gi
=0, их именуют прогоночными коэффициентами, и мы можем их отыскать по растущей рекурсии прямо до i=n-1. Можем записать:
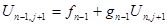 (3.18)
(3.18)
Подставим выражение (3.18) в уравнение для 2-ой границы (3.11) и выразим Un
,
j
+1
:
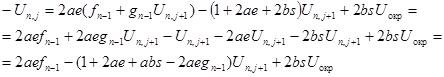 (3.19)
(3.19)
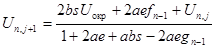 (3.20)
(3.20)
сейчас Un
,
j
+1
нам известна. Используя приобретенное выражение, определим Un
-1,
j
+1
из выражения (3.18) для всех i, включая i=1. Таковым образомUш,
j
+1
мы определяем по оборотной рекурсии от i+1 к i, в то время как fi
и gi
определяли по прямой рекурсии отi-1 к i. Таковой способ расчета дает меньшую погрешность.
3.3 Описание входных и выходных данных
Входными данными являются значения исходной температуры стены и температуры окружающей среды (К), длина стержня (м), коэффициенты теплоотдачи (Вт/м2
К) и теплопроводимости (Вт/мК), удельная теплоемкость (Дж/кгК), плотность (кг/м3). Выходные данные программки – график конфигурации температуры изолированного края стены во времени.
3.4 текст программки в
SciLab
//Данные значения
t0=873;
L=0.2;
alfa=100;
lamda=58.7;
c=500;
p=7900;
tos=233;
//количество шагов и шаг по длинe стержня
n=20;
dx=(L-0)/n;
//Шаг по времени, время,кол-во шагов и сетка по времени
dt=100;
time=70000;
m=time/dt;
T=0:dt:time;
//Изначальное распределение температур по стержню
for i=1:n+1
U(i,1)=t0;
end
//температура по длине стержня во времени по неявной схеме
l=dt/dx^2;
k=lamda/c/p;
b=alfa/c/p;
c=dt/dx;
g(1)=0;
for j=2:m+1
f(1)=U(1,j-1);
for i=2:n+1
f(i)=(k*l*f(i-1)+U(i,j-1))/(1+2*k*l-k*l*g(i-1));
g(i)=k*l/(1+2*k*l-k*l*g(i-1));
end
U(n+1,j)=(2*b*c*tos+2*k*l*f(n)+U(n+1,j-1))/(1+2*k*l+2*b*c-2*k*l*g(n));
for i=n:-1:2
U(i,j)=g(i)*U(i+1,j)+f(i);
end
U(1,j)=(U(1,j-1)+2*k*l*U(2,j))/(1+2*k*l);
end
//температура изолированного конца стержня
scf(1);
plot(T,U(n+1,:),’k-‘);
xgrid(1);
3.5 Результаты работы программки
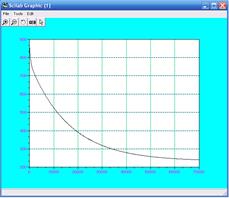
3.
5
Блок-схема программки
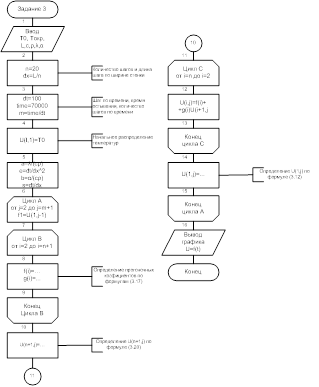
Набросок 3 – Блок-схема программки для расчета температурного режима плоской стены
Задание 4. Численные процедуры оценивания характеристик нелинейных регрессионных моделей
4.1 Постановка задачки
Пусть некий процесс описывается внутренне нелинейной моделью, т.е. таковой, которая не быть может представлена в линейном виде относительно характеристик. Будем находить уравнение модели в виде:
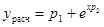 (4.1)
(4.1)
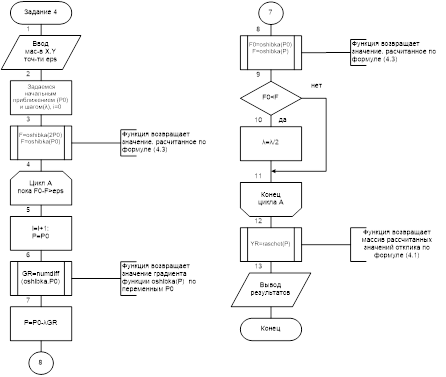
Требуется воплотить способ наискорейшего спуска поиска МНК оценок характеристик в нелинейных регрессионных моделях.
4.2 Математическая постановка задачки
В способе наискорейшего спуска направление движения при поиске минимума F(x) задается вектором антиградиента − gradF(p1
,p2
) функции F(p1
,p2
) в рассматриваемой точке, т.е:
(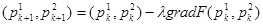 (4.2)
(4.2)
Функция F(p1
,p2
) расчитывается как квадрат ошибки расчетных и фактических значений отклика:
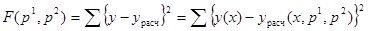 (4.3)
(4.3)
Составляющие вектора градиента в точке xk определяются значениями личных производных первого порядка функции F(x) по подходящим переменным, вычисленным в точке (p1
k
, p2
k
):
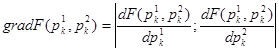 (4.4)
(4.4)
Направление вектора градиента совпадает с направлением наискорейшего возрастания функции F(p1
,p2
). Вектор − gradF(p1
,p2
) именуется антиградиентом, его направление совпадает с направлением наискорейшего убывания функции. Предполагается, что составляющие градиента могут быть записаны в аналитическом виде либо с довольно высочайшей точностью вычислены с помощью численных способов.
Выбор величины шага λ осуществляется методом решения задачки минимизации F(p1
,p2
) в направленииgradF(p1
,p2
) при помощи 1-го из способов одномерного поиска.
Преимущество способа в том, что при переходе от шага к шагу обеспечивается выполнение неравенстваF(p1
k
+1
,p2
k
+1
)<= F(p1
k
,p2
k
), т.е.
Скорость сходимости способа при решении неких задач является неприемлимо низкой.
Это соединено с тем, что конфигурации переменных конкретно зависят от величины градиента, которая стремится к нулю в округи точки минимума. Потому способ наискорейшего спуска эффективен при поиске на значимых расстояниях от точки минимума x* и плохо работает в округи данной точки.
4.3 Описание входных и выходных переменных
В качестве входных переменных имеем массив независящих значений Х и фактические значения отклика YF, точность вичислений eps.
Выходные величины – конечне значения p1
и p2
, при которых достигается минимум функции F(p1
,p2
), количество итераций, что охарактеризовывает скорость сходимости способа и значения отклика и таблицу с фактическим и расчетным значениями отклика.
4.4 текст программки в
SciLab
//Входные данные
X1=[1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6];
YF=[20 30 70 85 100 90 100 108 120 110 124]; //Y фактическое
//Расчетная функции в виде у=р1-р2expХ1)
function YR=raschet(P)
YR=P(1)-P(2)*exp(-X1);
endfunction
//Минимизируемая функция как итог
//ошибки расчетных и фактических значений
function F=oshibka(P)
F=sum((YF-raschet(P))^2);
endfunction
eps=0.00001; //точность вычислений
P=[10 0.9]; //изначальное приближение
lamda=1; //параметр,характеризующий длину шага
F0=oshibka(P*2);
F=oshibka(P);
i=0;
while абс(F0-F)>eps
i=i+1;
P0=P;
GR=numdiff(oshibka,P0);
P=P0-lamda*GR;
F0=oshibka(P0);
F=oshibka(P);
if F0<F
lamda=lamda/2;
end
end
значения р1 и р2, при которых ошибка расчетов мала’
p1=P(1)
p2=P(2)
Скорость схождения(количество циклов)’
i
Y=raschet(P);
‘Таблица результатов расчета’
[X1;YF;Y;(YF-Y)^2]’
‘Среднее квадратическое отклонение’
sigma=F
scf(1);
plot(X1,YF,’k.’,X1,Y,’k-‘);
xgrid(1);
4.5 Результаты работы программки
Значения р1 и р2, при которых ошибка расчетов мала
p1 = 110.90905
p2 = 282.44884
Скорость схождения(количество циклов)
i = 502.
Таблица результатов расчета
XYFYR (YF-YR)^2
1. 20. 7.0019302 168.94982
1.5 30. 47.886197 319.91604
2. 70. 72.683758 7.2025575
2.5 85. 87.724239 7.4214795
3. 100. 96.846752 9.9429717
3.5 90. 102.37984 153.26034
4. 100. 105.73582 32.899642
4.5 108. 107.77133 0.0522905
5. 120. 109.00593 120.86965
5.5 110. 109.75475 0.0601485
6. 124. 110.20893 190.19358
Среднее квадратическое отклонениеsigma = 1010.7685
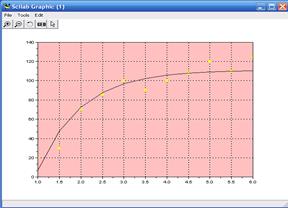
4.6 Блок-схема программки
Задание 5. Разработка аналитических моделей объектов автоматизации. Линеаризация моделей
5.1 Постановка задачки
Разработайте математическую модель данной динамической системы. Выстроить аналитическую модель емкости с одним притоком и 2-мя стоками (к примеру двухручьевая МНЛЗ) и провести ее линеаризацию. Математическую модель данного объекта представить в виде программки на ЭВМ , высчитать кривые начальной и линеаризованной модели отклика модели на ступенчатое и импульсное действие. Предложить методику идентификации характеристик модели. Какие опыты будет нужно провести на настоящем объекте? Оцените нужный размер и форму представления результатов.
5.2 Математическая постановка задачки
В данном объекте управления выходной величиной является уровень сплава в промежном ковше h, а входной величиной – разность меж притоком и стоками сплава ∆G=Gпр
-Gст1
-Gст2
, при этом возмущения могут возникать за счет конфигурации Gпр
,Gст1
и Gст2
.
Изменение уровня характеризуется последующим дифференциальным уравнением:
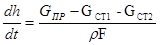 , (5.1)
, (5.1)
где ρ – плотность сплава, F – площадьзеркала сплава в промковше.
Понятно, что сток воды через отверстие пропорционален корню квадратному из высоты данной воды на отверстием:
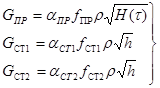 (5.2)
(5.2)
где αпр
,αст1
,αст2
– коэффициенты расхода на притоке и стоках; fпр
,fст1
,fст2
– проходные сечения в стопорных парах либо в шиберных затворах сталеразливочного и промежного ковшей; H(t) – текущее
С внедрение зависимостей (5.2) уравнение (5.1) приобретает вид нелинейного дифференциального уравнения первого порядка:
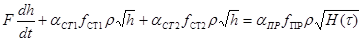 (5.3)
(5.3)
Уравнение можно несколько упростить, подвергнув линеаризации Gпр
,Gст1
и Gст2
, использовав разложение в ряд Тейлора Gпр
в округах точки Н0 и Gст1
и Gст2
в округах точки h0 и отбросив члены ряда, содержащие величины второго и наиболее порядков малости.
Введя некие обозначения и произведя перегруппировку членов, получим нелинейное дифференциальное уравнение:
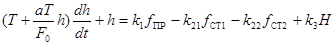 (5.4)
(5.4)
где H и h – уровни сплава в сталеразливочном и промежном ковшах;
Т – неизменная времени объекта;
k1
,k21
,k22
,k3
– коэффициенты передачи объекта по разным каналам возмущений.
Выражая номинальный расход сплава через сечение заготовки S и скорость разливки N, можно получить
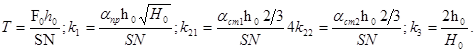 (5.5)
(5.5)
Таковым образом правая часть уравнения (5.4) учитывает четыре вероятных возмущения: по каналам регулирующих органов на притоке и стоках и каналу конфигурации уровня сплава в сталеразливочном ковше.
Решая уравнения (5.3) и (5.4) при помощи конечных разностей, получим последующие выражения для нелинеаризованной и линеаризованной моделей:
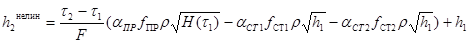 (5.6)
(5.6)
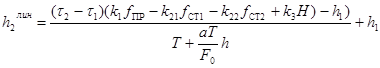 (5.7)
(5.7)
5.3 Результаты расчетов модели промежного ковша двухручьевой МНЛЗ
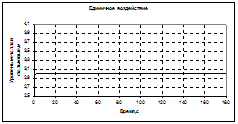
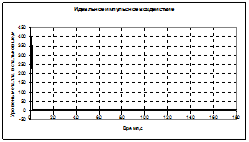
а) нелинеаризованная модель (формула (5.6)):
— установившийся режим

— единичное действие (функция Хевисайда)
— импульсное действие (функция Дирака)

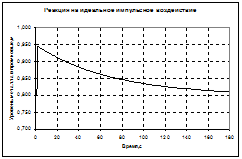
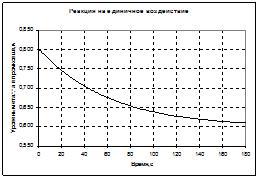
б) линеаризованная модель (формула (5.7)):
— единичное действие (функция Хевисайда)
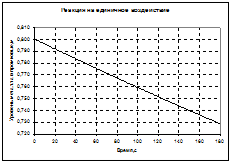
— импульсное действие (функция Дирака)
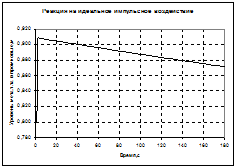
Графики построены для возмущения по каналу уровня сплава в сталеразливочном ковше.
Заключение
При выполнении данной курсовой работы были использованы способы идентификации статических и динамических объектов, изучены способы нелинейного оценивания и построена аналитическая модель объекта автоматизации. На мой взор, все примененные способы и принципы имеют весьма огромную роль в науке и технике, так как до этого чем выстроить какой-нибудь объект, необходимо поначалу изучить его модель, чтоб отдать заключение о его пригодности либо непригодности к решению поставленной задачки.]]>

