Учебная работа. Реферат: Решение дифференциальных уравнений 1 порядка методом Эйлера

Учебная работа. Реферат: Решение дифференциальных уравнений 1 порядка методом Эйлера

Содержание

Введение 3

1. Постановка задачки 5

2. Обзор имеющихся способов решения задачки 6 2.1.способ Рунге-Кутта 4-ого порядка для решения

уравнения первого порядка 6

2.2.задачка Коши 6

2.3.Способ Булирша- Штера с внедрением

рациональной экстраполяции для системы уравнений 7

2.4 Способ Адамса 8

2.5. Способ Эйлера 9

3. Описание алгоритмов решения задания 13

3.1. Описание переменных 13

3.2. Блок- схема головного модуля 14

3.3. Описание метода главной программки 14

3.4. Блок-схема функции “func” 15

3.5. Описание блок- схемы функции “func” 15

4. Описание программного обеспечения 16

4.1. Описание операционной системы 16

4.2. Описание языка программирования 18

4.3. Описание программки 19

5. Контрольный пример 21

6.анализ приобретенных результатов 22

Перечень литературы 24

Приложение 25

Введение

Уравнение именуется

если F определена и непрерывна в некой области и, во всяком случае, зависит от . Его решением является неважно какая функция

которая этому уравнению удовлетворяет при всех
в определённом конечном либо нескончаемом интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид

Решением этого уравнения на интервале I=[a,b] именуется функция

Решить дифференциальное уравнение у/
=f(x,y) численным способом — это означает для данной последовательности аргументов х0
, х1
…, хn
и числа у0
, не определяя функцию у=F(x), отыскать такие значения у1
, у2
,…, уn
, что уi
=F(xi
)(i=1,2,…, n) и F(x0
)=y0
.

Таковым образом, численные способы разрешают заместо нахождения функции y=F(x) (3) получить таблицу значений данной функции для данной последовательности аргументов. Величина h=xk
-xk-1
именуется шагом интегрирования.

способ Эйлера относиться к численным способам, дающим решение в виде таблицы приближенных значений разыскиваемой функции у(х). Он является сравнимо грубым и применяется в главном для приблизительных расчетов. Но идеи, положенные в базу способа Эйлера, являются начальными для ряда остальных способов.

способ Эйлера для обычных дифференциальных уравнений употребляется для решений почти всех задач естествознания в качестве математической модели. к примеру задачки электродинамики системы взаимодействующих тел (в модели вещественных точек), задачки хим кинетики, электронных цепей. Ряд принципиальных уравнений в личных производных в вариантах, допускающих разделение переменных, приводит к задачкам для обычных дифференциальных уравнений – это, как правило, краевые задачки (задачки о собственных колебаниях упругих балок и пластинок, определение диапазона собственных значений энергии частички в сферически-симметричных полях и почти все другое).

1.Постановка задачки

1.1. Решить приближенно дифференциальное уравнение вида способом Эйлера

1.2. Составить блок-схему метода для решения данного задания.

1.3. Создать программку на языке MicrosoftVisualC++

1.4. Протестировать программку на примере y’=2x+y (n=5, [0,1], y0=1)

1.5. Выполнить анализ результатов.

1.6. Оформить объяснительную записку с приложением.

2.Обзор способов решения задачки.

2.1.

Мысль Рунге-Кута заключается в том, чтоб применять способ неопределённых коэффициентов. Более употребительным способом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (2.1.1) является способ 4-ого порядка, в каком вычисления выполняются по формуле:

yk+1 = yk +(k1 +2k2 +2k3 +k4 )/6, (2.1.2)

k1 = Fk h = F(xk , yk )h

k2 = F(xk +h/2, yk +k1 /2)h

k3 = F(xk +h/2, yk +k2 /2)h

k4 = F(xk +h, yk +k3 )h,

k = 0, …, n-1

h = (xf -x0 )/n (2.1.3)

2.2.

Разглядим задачку Коши для уравнений первого порядка на отрезке [a,b]:

, (2.1.4)

Разобьём просвет [a,b] на Nчастей . Обозначим , где u(x) –четкое решение задачки Коши, и через значения приближенного решения в точках . Существует 2 типа численных схем :

1. очевидные: ) (2.2.1)

2. неявные: (2.2.2)

тут F некая функция, связывающая приближения. В очевидных схемах приближенное в точке определяется через некое число kуже определённых приближенных значений. В неявных схемах определяется не рекурентным методом, как в очевидных схемах, а для его определения возникает уравнение, так как равенство (2.2.2) представляет из себя конкретно уравнение на . Очевидные схемы проще, но часто неявные схемы лучше.

2.3.

Способ Булирша-Штера (Bulirsch-Stoer Method) — это способ решения системы обычных дифференциальных уравнений первого порядка с гладкими правыми частями. Гладкость правых частей является нужной для работы способа. Если правые части вашей системы не являются гладкими либо содержат разрывы, то лучше применять способ Рунге-Кутта. В случае же гладкой системы способ Булирша-Штера дозволяет достигнуть значительно большей точности, чем способ Рунге-Кутта.

Главный мыслью способа является вычисление состояния системы в точке x+h, как результата 2-ух шагов длины h/2, 4 шагов длины h/4, восьми шагов длины h/8 и так дальше с следующей экстраполяцией результатов. способ строит рациональную интерполирующую функцию, которая в точке h/2 проходит через состояние системы опосля 2-ух таковых шагов, в точке h/4 проходит через состояние системы опосля 4 таковых шагов, и т.д., а потом вычисляет

Гладкость правых частей приводит к тому, что вычисленное с помощью экстраполяции состояние системы оказывается весьма близко к реальному, а внедрение рациональной экстраполяции заместо полиномиальной дозволяет ещё больше повысить точность.

Таковым образом проводится один шаг способа, опосля что принимается решение — следует ли изменять шаг, а если да — то в какую сторону. При всем этом употребляется оценка погрешности, которую мы получаем в качестве доп результата при рациональной экстраполяции. Необходимо подчеркнуть, что метод решает автономную систему, т.е. если уравнения системы содержат время, то нужно ввести время в качестве переменной, производная от которой тождественно равна единице.

Рассмотренные выше способы являются очевидными одношаговыми (для нахождения следующего приближения употребляется только одно предшествующее). Приведённый ниже способ является многошаговым.

Пусть задана задачка Коши:

(2.4.1)

Для четкого решения (которое нам не понятно) выполнено:

(2.4.2)

Представим, нам известны приближенные значения функции



в
точках (стартовые
точек, а именно, можно отыскать способом Эйлера либо способом Рунге-Кутта того либо другого порядка), тогда функцию







в (2.4.2) для приближенного вычисления интеграла можно поменять на интерполяционный полином порядка

построенный по
точкам , интеграл от которого считается очевидно и представляет собой линейную комбинацию значений cнекоторыми множителями . Таковым образом, мы получаем последующую рекуррентную функцию вычисления приближенных значений функции



(являющимся четким решением задачки Коши) в точках :

(2.4.3)

Описанная схема является

шаговой очевидной формулой Адамса.

Пусть — интерполяционный полином порядка
, построенный по

значению б одно из которых, конкретно , мы будем считать неведомым. Модифицируем (2.4.3), заменив в нём на полином наиболее высочайшей степени , интеграл от которого выражается в виде линейной композиции значений с некими новенькими коэффициентами :

(2.4.4)

Формула (2.4.4) представляет собой неявную схему Адамса и является уравнением на , которое можно решать способом поочередных приближений. естественно, что изначальное приближение , обязано быть уместно выбрано. Для этого комфортно соединить очевидную и неявную схемы Адамса в одну, именуемую «способом корректировки». Конкретно при помощи очевидной схемы определяется изначальное приближение (прогноз), а потом по неявной схеме оно нужное число раз (обычно один либо два) корректируется способом поочередных приближений до заслуги данной точности (корректировка).

2.5.способ Эйлера.

Решить дифференциальное уравнение у/
=f(x,y) численным способом — это означает для данной последовательности аргументов х0
, х1
…, хn
и числа у0
, не определяя функцию у=F(x), отыскать такие значения у1
, у2
,…, уn
, что уi
=F(xi
)(i=1,2,…, n) и F(x0
)=y0
. (2.5.1)

Таковым образом, численные способы разрешают заместо нахождения функции

У=F(x) получить таблицу значений данной функции для данной последовательности аргументов. Величина h=xk
-xk-1
именуется

способ Эйлера относиться к численным способам, дающим решение в виде таблицы приближенных значений разыскиваемой функции у(х). Он является сравнимо грубым и применяется в главном для приблизительных расчетов. Но идеи, положенные в базу способа Эйлера, являются начальными для ряда остальных способов.

Разглядим дифференциальное уравнение первого порядка (2.5.1)

с исходным условием

x=x0
, y(x0
)=y0
(2.5.2)

Требуется отыскать решение уравнения (2.5.1) на отрезке [а,b].

Разобьем отрезок [a, b] на n равных частей и получим последовательность х0
, х1
, х2
,…, хn
, где xi
=x0
+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.

В способе Эйлера приближенные значения у(хi
)»yi
рассчитываются поочередно по формулам уi
+hf(xi
, yi
) (i=0,1,2…).

При всем этом разыскиваемая интегральная кривая у=у(х), проходящая через точку М0
(х0
, у0
), заменяется ломаной М0
М1
М2
… с верхушками Мi
(xi
, yi
) (i=0,1,2,…); каждое звено Мi
Mi
+1
данной ломаной, именуемой

имеет направление, совпадающее с направлением той интегральной кривой уравнения (2.5.1), которая проходит через точку Мi
. Если правая часть уравнения (2.5.1) в неком прямоугольнике R£a, удовлетворяет условиям:
|f(x, y1
)- f(x, y2
)| £N|y1
-y2
| (N=const), (2.5.3)

|df/dx|=|df/dx+f(df/dy)| £ M (M=const),

то имеет пространство последующая оценка погрешности:

|y(xn
)-yn
| £hM/2N[(1+hN)n
-1], (2.5.4)

где у(хn
)-

Формула (13) имеет в главном теоретическое применение. На практике время от времени оказывается наиболее комфортным
: поначалу расчет ведется с шагом h, потом шаг дробят и повторный расчет ведется с шагомh/2. Погрешность наиболее четкого значения уn
*
оценивается формулой

|yn
-y(xn
)|»|yn
*
-yn
|.(2.5.5)

способ Эйлера просто распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Крайние должны быть за ранее приведены к системе дифференциальных уравнений первого порядка.

Разглядим дифференциальное уравнение (2.5.1) y/
=f(x,y) с исходным условием y(x0
)=y0
. Разобьем наш участок интегрирования на n равных частей. На малом участинтегральную кривую заменим прямой линией.

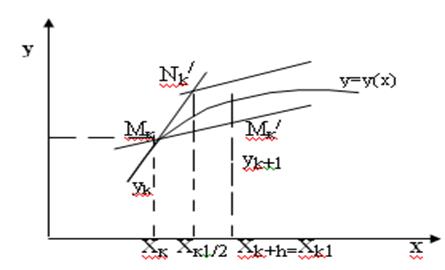
Рис.1 способ Эйлера в графическом видa

Получаем точку Мк
(хк
,ук
). Через Мк
проводим касательную: у=ук
=f(xk
,yk
)(x-xk
). Делим отрезок (хк
,хк1
) напополам:

xNk
/
=xk
+h/2=xk
+1/2
(2.5.6)

yNk
/
=yk
+f(xk
,yk
)h/2=yk
+yk
+1/2

Получаем точку Nk
/
. В данной точке строим последующую касательную:

y(xk
+1/2
)=f(xk
+1/2
, yk
+1/2
)=αk (2.5.7)

Из точки Мк
проводим прямую с угловым коэффициентом αк
и определяем точку пересечения данной прямой с прямой Хк1
. Получаем точку Мк
/
. В качестве ук+1
принимаем ординату точки Мк
/
. Тогда:

ук+1
=ук
+αк
h

xk
+1
=xk
+h

(2.5.8)αk
=f(xk
+
h/2
, yk
+f(xk
,Yk
)h/2)

yk
=yk
-1
+f(xk
-1
,yk
-1
)h

(2.5.8)-рекурентные формулы способа Эйлера.

Поначалу вычисляют вспомогательные значения разыскиваемой функции ук+1/2
в точках хк+1/2
, потом находят

Для оценки погрешности в точке хк
проводят вычисления ук
с шагом h, потом с шагом 2h и берут 1/3 различия этих значений:

| ук
*
-у(хк
)|=1/3(yk
*
-yk
),(2.5.9)

где у(х)-точное решение дифференциального уравнения.

Таковым образом, способом Эйлера можно решать уравнения всех порядков. к примеру, чтоб решить уравнение второго порядка y//
=f(y/
,y,x) c исходными критериями y/
(x0
)=y/
0
, y(x0
)=y0
, производится подмена:

y/
=z (2.5.10)

z/
=f(x,y,z)

Тем преобразуются исходные условия: y(x0
)=y0
, z(x0
)=z0
, z0
=y/
0
. (2.5.12)

3.Описание алгоритмов решения задачки

3.1.Описание переменных.

Изначальное




Конечное




количество шагов






Изначальное




Коэффициент при переменой x






Коэффициент при переменной y









Фиксированное приращение аргумента (x)






Расчётное Промежные







Счётчик цикла






Промежуточное




Промежуточное




Решение уравнения в точках f(Xprom,Yprom)






Функция f(x,y)

3.2. Блок- схема головного модуля

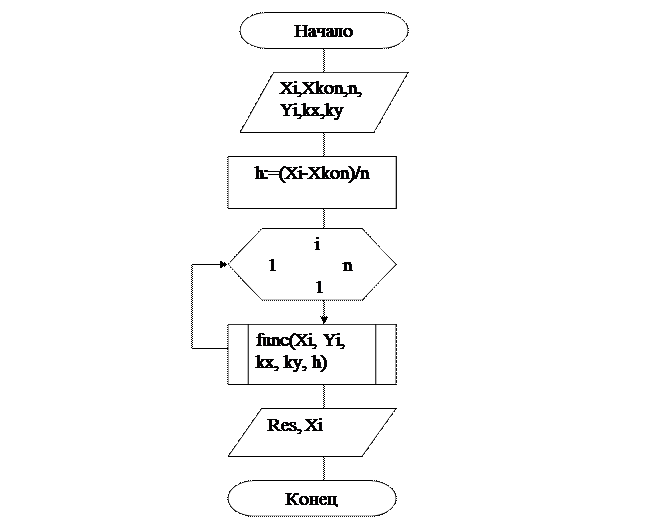
3.3 Описание метода главной программки.

Номер блока

Описание


1
Ввод исходного и конечного значений интервала вычисления уравнения, количество шагов, изначальное значение у, также коэффициенты при kxи ky.

2
Вычисление фиксированного приращения аргумента х

3
Цикл с шагом 1 и конечным значением не превосходящим количество шагов, который высчитывает значение yна определённом интервале

4
Функция для расчёта уравнения вида y’=f(x,y);

5

Вывод результатов на интервале X

3.4 Блок-схема функции “func”.

3.5 Описание блок- схемы функции “func”.

Номер

блока

Описание


1
Вычисление: функции f1 с подстановкой исходных значений; промежных значений Yprom и Xprom, значения aдля вычисления f(Xprom,Yprom) и расчёт результатов функции и переход на последующий шаг.

2
Приращение аргумента xна h

3
Вывод результатов уравнения и интервала

*Реализация метода на языке программирования C++ представлена в приложении .

4.Описание программного обеспечения.

4.1 Описание операционной системы

Основное требование к операционной системе (ОС), предъявляемое поставленной задачей, это наличие ANSI либо POSIX совместимого компилятора языка C++.

Для реализации задачки была выбрана крайняя клиентская версия операционной системы Microsoft, основанная на ядре NT – MicrosoftWindowsXPProfessional.

Обозначенная операционная система владеет преимуществ:

· наличие достаточного количество ANSI либо POSIX совместимых компиляторов языка C++, разработанных для данной ОС, а конкретно –

o Microsoft C++ (version 2-6)

o gcc

o Borland C++

o Intel C++

o остальные;

· достаточная маневренность, надежность и сохранность;

· обширное распространение основанных на ядре NT операционных систем Microsoft, совместимых по программному обеспечению с WindowsXPProfessional (NT/2000/XP/2003 – client & server);

· высочайшая скорость работы приложений, разработанных для данной ОС с внедрением компиляторов C++.

Начальный код программки быть может откомпилирован и под иной операционной системой, если для такой имеется ANSI либо POSIX совместимый компилятор языка C++.

программка была протестирована на операционной системе MicrosoftWindowsXPProfessionalSP1.

Технические данные :

· HDD: 60 Gb

· машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) (либо вычислительной системы) которое делает арифметические и логические операции данные программкой преобразования инфы управляет вычислительным действием и коор x86 Family 15 Model 2 Stepping 7 GenuineIntel ~1817 МГц

· версия BIOS Award Software International, Inc. F4, 06.03.2003

· Аппаратно-зависимый уровень (HAL) версия = «5.1.2600.1106 (xpsp1.020828-1920)»

· Полный размер физической памяти 256,00 МБ

· Доступно физической памяти 29,97 МБ

· Всего виртуальной памяти 873,69 МБ

· Доступно виртуальной памяти 350,04 МБ

· файл подкачки 618,21 МБ

4.2 Описание языка программирования

язык программирования С++

С++ — это всепригодный язык программирования, загаданный так, чтоб создать программирование наиболее приятным для сурового программера. Кроме второстепенных деталей С++ является надмножеством языка программирования C. Кроме способностей, которые дает C, С++ предоставляет гибкие и действенные средства определения новейших типов. Используя определения новейших типов, буквально отвечающих концепциям приложения, программер может делить разрабатываемую программку на лег ко поддающиеся контролю части. Таковой способ построения программ нередко именуют абстракцией данных. информация о типах содержится в неких объектах типов, определенных юзером. Такие объекты ординарны и надежны в использовании в тех ситуациях, когда их тип недозволено установить на стадии компиляции. Программирование с применением таковых объектов нередко именуют объектно-ориентированным. При правильном использовании этот способ дает наиболее недлинные, проще понимаемые и легче управляемые программки.

В С++ нет типов данных высочайшего уровня и нет первичных операций высочайшего уровня. В нем нет, к примеру, матричного типа с операцией воззвания либо типа строчка с операцией конкатенации. Если юзеру пригодятся подобные типы, их можно найти в самом языке. На самом деле дела, основное, чем занимается программирование на С++ — это определение всепригодных и специально-прикладных типов. Отлично разработанный тип, определяемый юзером, различается от встроенного типа лишь методом определения, но не методом использования.

Реализация С++ весьма просто переносима. Но есть полные основания применять С++ в среде, где имеется еще наиболее значимая поддержка. Такие средства, как динамическая загрузка, пошаговая трансляция и база данных определений типов могут с полезностью применяться без действия на язык.

Типы и средства сокрытия данных в С++ опираются на проводимый во время компиляции анализ программ с целью предотвращения случайного преломления данных. Они не обеспечивают секретности либо защиты от предумышленного нарушения правил. Но эти средства можно применять без ограничений, что не приводит к доп расходам времени на выполнение либо места памяти.

Компилятор MicrosoftC++ и среда разработки MicrosoftVisualStudio

В качестве компилятора для разработки приложения был избран MicrosoftC++ по последующим причинам:

· фактически полная сопоставимость со эталоном ANSIC++;

· наличие комфортной среды разработки MicrosoftVisualStudio;

· наличие хорошей документации;

· высочайшая скорость работы результирующих приложений;

· сопоставимость разработанных приложений с огромным количеством обширно всераспространенных операционных систем;

· достаточная скорость компиляции.

4.3 Описание программки

Разработанное приложение поставляется в виде 2-ух файлов:

1. methodEulera.cpp – начальный код программки на языке C++;

2. methodEulera.exe – исполняемый файл.

Для выполнения исполняемого файла нужна одна из ниже перечисленных операционных систем:

· Microsoft Windows 3.11+Win32s;

· Microsoft Windows 95/98/Me;

· MicrosoftWindowsNT/2000/XP/2003 – клиентская либо серверная версия.

Программка не просит подготовительной установки и быть может сходу же запущена на выполнение.

Начальный код приложения быть может откомпилирован в любом ANSI либо POSIX совместимом компиляторе С++ для получения выполнимой программки. Для удачной компиляции требуется наличие обычной библиотеки «iostream».

5. Контрольный пример

Данный способ протестирован на контрольном примере и реализован при помощи языка программирования С++.

В итоге вычислений контрольного примера вида y’=2
x+
y
с интервалом [0,1],

количеством шагов равному 5
и исходным условием у
равным 1
, при помощи программки, вышли последующие результаты:

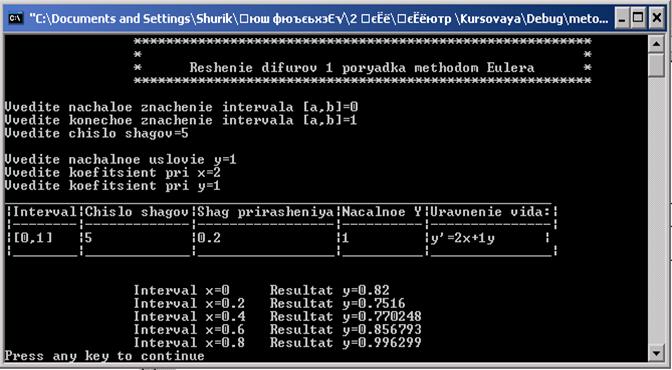Рис. 2. Экран с плодами выполнения программки.

Как видно, при вычислении программка на первом шаге берёт исходные значения для вычисления, а на следующих берёт значения приобретенные с прошлых шагов. Можно прийти к выводу, что точность вычисления данного способа зависит от количества избранных шагов: чем больше шагов, тем меньше фиксированное приращение , а как следует она наиболее буквально вычисляет

По работе программки сделалось видно, что с её внедрением намного упростилась работа юзера. юзер просто вводит интервал на котором должен рассчитываться пример, количество шагов и изначальное значения и программка выдаёт уже готовое решение данного примера.

6.анализ приобретенных результатов.

По результатам программки можно составить таблицу сопоставления результатов приобретенных при использовании программки и результатов, приобретенных ручным методом:

Ручной метод вычисления

Программный метод вычисления


Х
Y
X
Y

0
0,82
0
0,82

0,2
0,75
0,2
0,7516

0,4
0,77
0,4
0,770248

0,6
0,85
0,6
0,856793

0,8
0,99
0,8
0,996299

Из приведенного сопоставления можно прийти к выводу, что один итог различается от другого тем, что в примере, решенном программным методом ответ рассчитывается с большей точностью, чем при ручном методе. Это быть может соединено с тем, что в ручном методе итог округляется для удобства вычисления примера.

Решение дифференциальных уравнений способом Эйлера можно также показать в графическом виде:

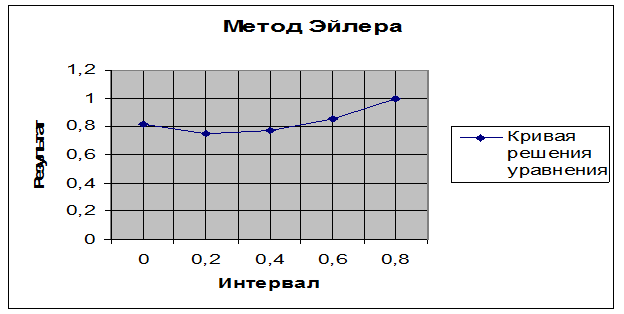
Рис.3.Графическое изображение решения примера y’=2x+y

Как видно из рис.3 графиком решения уравнения является кривая , форма которой зависит от количества разбиений интервала.

По результатам выполненной работы можно прийти к выводу, что решение дифференциальных уравнений способом Эйлера является способом вычисления со средней точностью и точность вычисления данного способа зависит от количества разбиений интервала интегрирования. При сопоставлении результатов решенными различными методами можно сказать, что данный способ был правильно реализован на языке программирования MicrosoftVisualC++. Приобретенные результаты сходятся с маленький погрешностью.

Перечень литературы.

1. Численные способы (анализ, алгебра, простые дифференциальные уравнения), Н.С. Бахвалов. Основная редакция физико- математической литературы изд-ва «Наука», М., 1975г.

2. способы, теории обычных дифференциальных уравнений. Н.И. Гаврилов . Государственное издательство «Высшая школа» Москва-1962г.

3. В.В.Пак., Ю.Л. Носенко. Высшая математика: Учебник.- Д.: Сталкер, 1997г.

4. Б. П. Демидович, И. А. Марон Базы вычислительной арифметике. – М., 1966

5. Загускин В. Л. – Справочник по численным способам решения уравнений. – М.: ФИЗМАТГИЗ, 1960. – 216 с.

6. Либерти, Джесс.

Освой без помощи других С++ за 21 денек, 4-е издание.:Пер с англ.-М.: Издательский дом «Вильямс», 2003.-832с.

7. П.Нортон, П.Иао «Программирование на С++ в среде Windows» («Диалектика» Киев 2003г.)

8. Янг М. Microsoft Visual C++ — М.:ЭНТРОП, 2000.

9. Марченко А.И., Марченко Л.А. – Программирование в среде

Turbo Pascal 7.0 – К.: ВЕК+, М.: Двучлен Универсал, 1998. – 496 с.

10. Высшая математика: Справ. материалы: Книжка для учащихся .- М.:

Просвещение, 1988.-416 с.: ил.

приложение.

Листинг программки.

#include<iostream>

using namespace std;

void func(double& Xi, double& Yi,double kx, double ky, double h);

int main()

{

double h,Xi,Yi,Xkon,kx,ky;

int n;

cout<<«t»<<«t»<<«************************************************n»;

cout<<«t»<<«t»<<«* * «<<«n»;

cout<<«t»<<«t»<<«* Reshenie difurov 1 poryadka methodom Eulera *»<<«n»;

cout<<«t»<<«t»<<«*************************************************

cout<<endl;

cout<<«Vvedite nachaloe znachenie intervala [a,b]=»;

cin>>Xi;

cout<<«Vvedite konechoe znachenie intervala [a,b]=»;

cin>>Xkon;

cout<<«Vvedite chislo shagov=»;

cin>>n;

h=(Xkon- Xi)/n;

cout<<endl;

cout<<«Vvedite nachalnoe uslovie y=»;

cin>>Yi;

cout<<«Vvedite koefitsient pri x=»;

cin>>kx;

cout<<«Vvedite koefitsient pri y=»;

cin>>ky;

cout<<«|Interval|Chislo shagov|Shag prirasheniya|Nacalnoe Y|Uravnenie vida:| «<<«n»;

cout<<«|———|————-|——————|———-|—————|»<<«n»;

cout<<«|»<<«[«<<Xi<<