Учебная работа. Доклад: Геометрическая алгебра: машина времени
Внедрение геометрических чертежей как иллюстрации алгебраических соотношений встречалось еще в Старом Египте и Вавилоне. к примеру, при решении уравнений с 2-мя неведомыми, одно именовалось “длиной”, другое -”шириной”. Произведение неведомых называли “площадью”. В задачках, приводящих к кубическому уравнению, встречалась 3-я неведомая величина — “глубина”, а произведение 3-х неведомых называлось “объемом”.
Но недозволено дозволить геометрическим терминам ввести нас в заблуждение. Вавилоняне мыслили, до этого всего, алгебраически. Хотя они изображали для наглядности неведомые числа линиями и площадями, но крайние всё же постоянно оставались числами. Это проявлялось уже в том, что с неведомыми величинами, по наименованию имеющими разные измерения, обращались как с однородными: “площадь” складывали со “стороной”, от “размера” отымали “площадь” и так дальше.
Решение уравнений в Старом Вавилоне.
Древнейшие египтяне и вавилоняне излагали свои алгебраические зания в числовой форме. Они не знали ни отрицательных чисел, ни, тем наиболее всеохватывающих и уравнения, не имеющие положительных корней ими не рассматривались. Все задачки и их решения излагались словесно.
В одной из клинописных табличек встречается таковая задачка: “Я вычел из площади сторону моего квадрата, это 870” (несложно додуматься, что речь идет о квадратном уравнении x2
-x=870).
Решение его в табличке рекомендуется находить последующим образом: “Ты берешь 1, число. Делишь напополам 1, это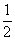 . Умножаешь
. Умножаешь 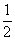 на
на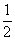 , это
, это . Ты складываешь это с 870, и это есть
. Ты складываешь это с 870, и это есть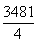 , что является квадратом для
, что является квадратом для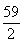 .Ты складываешь
.Ты складываешь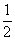 , которую ты множил, с
, которую ты множил, с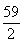 , получаешь 30, сторона квадрата”.
, получаешь 30, сторона квадрата”.
Все числа в табличке записаны в 60-ричной системе счисления, а мы приводим их в десятичной записи. В обычных нам обозначениях предложенные деяния принимают вид: . В данной нам записи угадывается формула вычисления корней приведенного квадратного уравнения.
. В данной нам записи угадывается формула вычисления корней приведенного квадратного уравнения.
Старая Греция.
совершенно иной вид приняла алгебра в Старой Греции. Опосля открытия пифагорейцами несоизмеримых величин чертежи из средства наглядности перевоплотился в главный элемент алгебры.
Более принципиальным, посреди приписываемых пифагорейцам 5 века до н.э. достижений, было открытие несоизмеримых отрезков.
Появлялось оно, быстрее всего, из попыток отыскать общую меру диагонали и стороны квадрата.
Это открытие потрясло базы пифагорейской философии. Ведь из него следует, что число не всемогуще, потому что есть отрезки, отношение которых не выражается отношением целых чисел (а остальных чисел пифагорейцы не знали).
Оказалось, что если не выходить за рамки пифагорейского учения о числе, то почти все задачки, приводящие к квадратным уравнениям, совершенно не имеют числового решения.
Даже такое обычное уравнение, как x2
=2, не быть может принято решение ни в области целых чисел, ни даже в области отношений чисел. Но оно оказывалось полностью разрешимым в области прямолинейных отрезков: его решением являлось диагональ квадрата со стороной, равной единице.
Не решаясь поменять свою трактовку числа, пифагорейцы перебежали из области чисел в область геометрических величин, построив соответственное исчисление. Для построения такового исчисления пифагорейская математика располагала всем нужным. необходимо было лишь поменять взор на роль чертежей, превратив их из средства наглядности в главный элемент алгебры, и логически расположить весь имеющийся материал.
Эта работа была выполнена пифагорейцами, а ее результаты потом включены Евклидом во вторую книжку “Начал”. Новое исчисление получило потом заглавие “геометрической алгебры”. В этом исчислении величины стали изображаться при помощи отрезков и прямоугольников, а любые утверждения и подтверждения имели Право на существование лишь в этом случае, если они давались на геометрическом языке. Древнегреческие арифметики работали не с числами, а с отрезками. Потому отыскать неведомое для их означало выстроить разыскиваемый отрезок.
Арабские страны.
Выделение алгебры (как науки о уравнениях) в самостоятельную ветвь арифметики вышло в арабских странах, куда опосля распада Римской империи переместился центр научной деятель.
В первой половине IX века в Багдаде работал Мухаммед ибн Муса ал-Хорезми ал-Маджуси (Мухаммед отпрыск Мусы из Хорезма из рода жрецов). Сохранились его сочинения по математики, алгебре, астрономии, географии и календарным расчетам. Более значимым является трактат ал-Хорезми по алгебре, в каком он разработал правила преобразования уравнений. Уравнения, естественно, были с числовыми коэффициентами и выражались в словесной форме. Но на этих определенных примерах ал-Хорезми указывает методы решения главных типов линейных и квадратных уравнений. В греческих традициях он строго геометрически доказывает свои методы.
Вослед за ал-Хорезми решению уравнений посвящают свои труды почти все арабские ученые ( Омар Хайям, ал-Бируни, ал-Каши и др.) Они изучали уравнения третьей и четвертой степени, корешки которых находятся с помощью пересечения парабол, гипербол и окружностей. Таковым методом решали задачки и греческие геометры. Но арабских ученых, чья математика тяготела к вычислениям, заинтересовывало и численное
Франция, Великобритания.
Геометрический путь, непременно, был превосходной находкой древних математиков. Но, к огорчению, он сдерживал предстоящее развитие алгебры. Ведь геометрически можно выразить только 1-ые степени (длины), квадратные (площади) и кубы (объемы), но не высшие степени неведомых. Ну и неведомые в этом случае могут быть лишь положительными числами. В конце концов, заместо алгебраических преобразований приходилось создавать геометрические построения, нередко весьма массивные. Чтоб выстроить неведомое, время от времени необходимо было быть подлинным виртуозом — это шло на пользу геометрии, но не алгебре.
В первой половине XVII века значимый шаг вперед в арифметизации алгебры сделал французский ученый Рене Декарт. Он не отделял учение о числах от учения о величинах, не соблюдал принципа однородности и старался высвободить алгебру от подчинения геометрии.
В трудах европейских ученых XVII-XVIII веков ясно проявляется арифметическое построение алгебры. И если во “Всеобщей математике” Ньютона огромное пространство еще занимают геометрические приложения, то уже в “Началах алгебры” Клеро и “Всепригодной математике” Эйлера все изложение алгебры носило чисто арифметический нрав.
]]>

 (5 оценок, среднее: 4,80 из 5)
(5 оценок, среднее: 4,80 из 5)