Учебная работа. Доклад: Гравитация и геометрические свойства пространства

Учебная работа. Доклад: Гравитация и геометрические свойства пространства

Очень слабенькие гравитационные силы на современном шаге развития Вселенной играют определяющую роль в действиях галлактического масштаба, где электромагнитные взаимодействия оказываются в значимой степени скомпенсированными за счет существования равного количества разноименных зарядов, а кратко действующие ядерные силы появляются лишь областях сосредоточения плотного и жаркого вещества. Современное осознание механизма появления гравитационных сил сделалось вероятным только опосля сотворения Теории Относительности, т.е. практически через три столетия опосля открытия Ньютонам закона Глобального тяготения.

Силы инерции.

Созданию современной теории гравитации предшествовало понимание глубочайшей связи, имеющейся меж силами тяготения и псевдосилами инерции. Крайние с традиционной точки зрения не являются мерой настоящего взаимодействия меж телами, а вводятся в неинерциальных системах отсчета чисто формально для обеспечения способности записи в их уравнений движения, совпадающих по форме со Вторым законом Ньютона. Так все пассажиры снутри равноускоренно передвигающегося автобуса относительно связанной с ним неинерциальной системы отсчета “летят к стене” с схожим убыстрением (равным убыстрению автобуса), оставаясь “по сути” недвижными относительно “неплохой” инерциальной системы отсчета, связанной с Землей. Для разъяснения этого явления исходя из убеждений находящегося в автобусе наблюдающего приходится представить, что при убыстрении на все объекты действуют силы инерции, пропорциональные их массе и приводящие к схожим убыстрениям:

(1) .

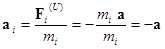При вращательном движении неинерциальных систем отсчета выражение для силы инерции приобретет наиболее непростой вид (а именно возникает слагаемое, зависящее от скорости движения тела — Криолисова сила наличие которой “разъясняет” асимметрию размывания берегов рек, текущих в перпендикулярном вращению Земли направлении и вращение плоскости колебаний маятника Фуко).

Индивидуальности гравитационных сил.

Принцип эквивалентности. Сформулированный И.Ньютоном закон гравитации по форме очень идентичен с законом Кулона:

(2) ,

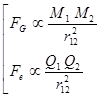что дозволяет по аналогии с электронным зарядом ввести гравитационный заряд (либо гравитационную массу) — меру возможности тел участвовать в гравитационных взаимодействиях. Гравитационная масса оказывается строго пропорциональной массе инертной (вводимой как коэффициент пропорциональности меж силой и убыстрением во 2-м законе Ньютона). Конкретно эта пропорциональность дозволила определять гравитационные заряды в тех же единицах, что и инертную массу (коэффициент пропорциональности “спрятан” в гравитационную постоянную).

Пропорциональность гравитационной силы инертной массе делает ее очень идентичной с силой инерции. А именно при поступательном движении неинерциальной системы отсчета с убыстрением, равным убыстрению вольного падения, вдоль направления гравитационных сил наступает полная компенсация сил тяготения и инерции — явление невесомости. Помещенный в закрытый лифт наблюдающий, ощущая исчезновение веса не может решить, что вышло в реальности: или лифт начал падать вниз с убыстрением вольного падения, или пропало гравитационное поле Земли.

Обобщая описанный мысленный понятие гравитационных взаимодействий, факт наличия либо отсутствия которых установить опытным методом, совершенно говоря, оказывается неосуществимым. Наблюдаемые же на опыте отличия линии движения тел, перемещающихся поблизости мощных объектов трактуются не как итог взаимодействия, как следствие искривления места.

Искривленное место владеет геометрическими качествами, значительно отличающимися от евклидового. В математическом формализме понятие кривизны места тесновато соединено с видом матрицы его метрического тензора — совокупы чисел 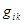, входящих в обобщенное определение скалярного произведения векторов:

(4) .

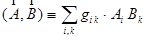Обычно эту совокупа записывают в виде таблицы (матрицы) размерами 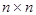(где n — размерность места):

(5) .

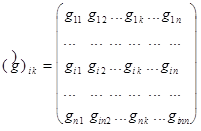В личных вариантах трехмерного евклидового места и четырехмерного псевдоевклидового места Минковского метрические тензоры имеют вид:

(6) ;

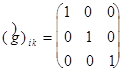
(7) ,

т.е. представляющие их матрицы диагональны. Такие места являются неискривленными.

Если же матрица метрического тензора места содержит недиагональные элементы, место оказывается искривленными. к примеру, метрический тензор двумерного искривленного места — поверхности сферы имеет вид:

(7) .

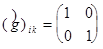Главные идеи Общей Теории Относительности.

Исходя из разработанной им Специальной Теории Относительности А.Эйнштейн сделал вывод о том, что помещенный в неинерциальную систему отсчета наблюдающий должен зарегистрировать наличие искривления места. Вправду, находящийся на вращающемся диске наблюдающий, измеряющий отношение длины окружности к радиусу, получит число, хорошее от 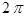, так как исходя из убеждений покоящегося наблюдающего идеал длины будет изменять свои размеры при поворотах относительно обусловленной вращением диска скорости (рис. 14_1).

Беря во внимание аналогию возникающих в неинерциальных системах отсчета сил инерции с гравитационными, А.Эйнштейн представил, что мощные тела вызывают вокруг себя локальное искривление четырехмерного пространства-времени:

(8) .

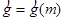Обобщением закона инерции Галилея на вариант искривленных пространств является утверждение о том, что глобальными линиями вольных тел являются геодезические (кривые, надлежащие минимальному собственному времени движения меж данными 2-мя точками). движение вдоль геодезической в искривленном пространстве исходя из убеждений трехмерного наблюдающего воспринимается как движение по трехмерной кривой с переменной скоростью, что в рамках традиционного подхода “разъясняется” действием гравитационных сил.

Уравнений гравитации в Общей Теории Относительности являются нелинейными: при наличии огромных масс принцип суперпозиции нарушается.

Экспериментальное доказательство ОТО. Релятивистская теория гравитации удовлетворяет принципу соответствия ( в пределе малых масс и скоростей из нее конкретно выводится законГлобального тяготения Ньютона ). В то же время уравнения гравитации предвещают ряд наблюдаемых эффектов, не поддающихся объяснению с позиций традиционной физики:

1. Прецессия эллиптических орбит планет, передвигающихся в поле сферических тел (зарегистрирована у наиблежайшей к Солнцу планетки — Меркурия).

2. Эффект “абсолютного” замедления времени в гравитационном поле либо при ускоренном движении (зарегистрирован по измерению времени распада нестабильных ядер и “красноватому смещению” световых волн в гравитационном поле).

3. Искривление лучей света поблизости мощных тел, хорошее по величине от эффекта, предсказываемого традиционной теории (наблюдается по изменению видимого положения звезд поблизости края Солнца).

Одним из более весомых аргументов в пользу корректности ОТО является ее внутренняя логичность, краса и элегантность.

Трудности сотворения Общей Теории Поля. Опосля сотворения ОТО появилась очень заманчивая перспектива выстроит единое описание всех взаимодействий в природе, объяснив их надлежащими искривлениями места (“Общая Теория Поля”). А.Эйнштейн не сумел воплотить эту программку, потерпели беды и бессчетные пробы его последователей. С нынешней точки зрения возможность построения таковой теории в рамках чисто Эйнштейновского подхода представляется проблематической, так как в построении теории электромагнитных взаимодействий был изготовлен очень большой шаг, заключающийся в разработке квантовой механики, основополагающие идеи которой выходят далековато за рамки Теории относительности.

Создание Теории Относительности было первым шагом в построении современной концепции естествознания. Ее роль состояла не только лишь в уточнении и обобщении традиционных формул: было показано, что познания о внешнем мире не носят абсолютного нрава и могут претерпевать значительные уточнения и конфигурации в процессе развития науки. Описывающая реально наблюдаемые явления природы теория может базироваться на утверждениях и идеях, не постоянно согласующихся с принятым воззрением и “здравым смыслом”, являющимся обобщением ежедневного опыта.

]]>