Учебная работа. Курсовая работа: Программная реализация алгоритма Дейкстры построение цепей минимальной длины
ХАРКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ РАДИОЭЛЕКТРОНИКИ
Кафедра информатики
КУРСОВАЯ РАБОТА
Тема: “Программная реализация метода Дейкстры (построение цепей малой длины)”
по дисциплине «Программирование»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Выполнил: Руководители:
Студент группы КИ-05-4 Руденко Д. А.
Петров О. В. Машталир С. В.
Харьков 2006
РЕФЕРАТ
Записка пояснительная к курсовой работе: 23с., 5 рис., 1 табл., 5 разделов, 3 приложения.
объект исследования – граф с взвешенными дугами.
Цель работы – разработка демонстрационной программки использования метода Дейкстры.
способ исследования – исследование литературы, составление и отладка программки на компе.
Данную программку можно употреблять для поиска кратчайших расстояний меж 2-мя точками.
программка составлена на языке С++в среде Microsoft Visual C++ 6.0. Главные слова: АЛГОРИТМ ДЕЙКСТРЫ, ГРАФ, ВЕРШИНА, РЕБРО, ВЕС, ПУТЬ, МАССИВ, МЕТКА,программка, ТИП, ОПЕРАТОР, ФУНКЦИЯ, ЦИКЛ, МАТРИЦА СМЕЖНОСТИ.
СОДЕРЖАНИЕ
Введение………………………………………………………….……
4
1 Постановка задачки и сфера её внедрения…..……………………
6
2 Теоретическая часть…………………………………….…………..
7
2.1 Общие сведения о графах…………………………………….
7
2.2 метод Дейкстры….………………………………………
9
3 Индивидуальности работы в среде ……………………….…………….
10
4 Программная реализация………………………………….…….
11
4.1 Описание метода и структуры программки……………..
11
4.2 Описание программных средств…………………………….
13
5 {Инструкция} юзера………………………………………….
15
Заключение….…………………………………………………….….
16
Список ссылок………………………………………………………
17
приложение А Текст программки…………………………………..
18
Приложение Б Итог………..……………………………….…..
22
приложение В Схема программной реализации метода Дейкстры…..
23
ВВЕДЕНИЕ
Благодаря собственному широкому применению, теория о нахождении кратчайших путей в крайнее время активно развивается.
Нахождение кратчайшего пути – актуально нужно и употребляется фактически всюду, начиная от нахождения рационального маршрута меж 2-мя объектами на местности (к примеру, кратчайший путь от дома до института), в системах автопилота, для нахождения рационального маршрута при перевозках, коммутации информационного пакета в Internet и т.п.
Кратчайший путь рассматривается с помощью некого математического объекта, именуемого графом.
Есть три более действенных метода нахождения кратчайшего пути:
· метод Дейкстры (употребляется для нахождения рационального маршрута меж 2-мя верхушками);
· метод Флойда (для нахождения рационального маршрута меж всеми парами вершин);
· метод Йена (для нахождения k-оптимальных маршрутов меж 2-мя верхушками).
Обозначенные методы просто производятся при малом количестве вершин в графе. При увеличении их количества задачка поиска кратчайшего пути усложняется. Тут на помощь приходит современная техника
Компьютерные средства и информационные технологии повысили способности такового комплексного способа исследования и сотворения, как моделирования объектов, явлений и действий – как тех, что есть в природе, так и тех, что создаются человеком искусственно.
количество объектов усложнялись, увеличивались, и натурное моделирование (макеты сооружений) сделалось нерентабельным, неэкономным. Потому для исследования начали использовать арифметику. Внедрение математических моделей – уравнения, неравенства, формулы и тому схожее именуется математическим моделированием, для развития и приспособления которого необходимы были действенные численные способы.
Воплотить большенный потенциал математического моделирования нереально без массивных средств автоматизации вычислений, которыми являются компы. Благодаря возникновению компов и развитию информационных технологий создаются способы и средства компьютерного моделирования, способные решать сложные практические задачки, такие как управление большенными энергетическими системами, создание достоверных прогнозов погоды либо урожая, моделирование региональных и общегосударственных систем, проектирование самолетов, кораблей и т. п. Компьютерная модель – это размещенная в компе совокупа средств, что реализуют теорию вычисления.
Для реализации компьютерной модели, огромное комп это просто набор разных устройств, микросхем, который не быть может полезным.
Огромные программки из-за собственной трудности часто содержат ошибки, которые могут стать предпосылкой вещественного вреда, а время от времени и грозить жизни людей (к примеру, при управлении авиаполётами). В итоге борьбы с неувязкой трудности программного кода были выработаны три новейшие концепции программирования:
а) объектно-ориентированное программирование (ООП);
б) унифицированный язык моделирования (UML);
в) спец средства разработки программного обеспечения;
Из всех объектно-ориентированных языков С++ является более обширно применяемым. И конкретно с его помощью в данном курсовом проекте реализуется метод Дейкстры.
1 ПОСТАНОВКА задачки И СФЕРА ЕЁ ПРИМЕНЕНИЯ
Главный задачей данного курсового проекта является программная реализация метода поиска кратчайшего пути меж 2-мя хоть какими верхушками графа.
программка обязана работать так, чтоб юзер вводил количество вершин и длины рёбер графа, а опосля обработки этих данных на экран выводился кратчайший путь меж 2-мя данными верхушками и его длина. нужно предугадать разные финалы поиска, чтоб программка не выдавала ошибок и работала верно.
Данная программка может употребляться в дискретной арифметике для исследования графов либо в качестве приятного пособия, демонстрирующего применение метода Дейкстры на практике.
2 ТЕОРЕТИЧЕСКАЯ часть
2.1 Сведения о графах
Граф G (рис.2.1.1) задается обилием точек (вершин) х1
, х2
,…, хn
. (которое обозначается через Х) и обилием линий (ребер) а1
, а2
,…,аm
. (которое обозначается эмблемой А), соединяющих меж собой все либо часть этих точек. Таковым образом, граф G стопроцентно задается (и обозначается) парой (Х, А). Если ребра из огромного количества А нацелены, что обычно показывается стрелкой, то они именуются дугами, и граф с таковыми ребрами именуется нацеленным графом.
рис.2.1.2
рис.2.1.1


к примеру, если дорога имеет не двух-, а однобокое движение то направление этого движения будет показано стрелкой.
Если ребра не имеют ориентации, то граф именуется неориентированным, (обоестороннее движение).
В направленном графе дуга обозначается упорядоченной парой, состоящей из исходной и конечной вершин, ее направление предполагается данным от первой верхушки ко 2-ой.
Методом (либо нацеленным маршрутом) нацеленного графа именуется последовательность дуг, в какой конечная верхушка всякой дуги, хорошей от крайней, является исходной верхушкой последующей.
Так, на рис. 2.1.2 способами являются последовательности дуг:
а6
, а5
, а9
, а8
, а4
. (1)
а1
, а6
, а5
, а9
. (2)
а1
, а6
, а5
, а9
, а10
, а6
, а4
. (3)
Направленной цепью (орцепью) именуется таковой путь, в каком любая дуга употребляется не больше 1-го раза.
Обычной орцепью именуется таковой путь, в каком любая верхушка употребляется не наиболее 1-го раза. К примеру, путь (2).
Маршрут есть неориентированный “двойник” пути, и это понятие рассматривается в тех вариантах, когда можно пренебречь направленностью дуг в графе. Таковым образом, маршрут есть последовательность ребер ä1
, ä2
,…, äq
, в какой каждое ребро аi
,
кроме первого и крайнего ребер, соединено с ребрами аi-1
и аi+1
своими концевыми верхушками. Последовательности дуг:
ä2
, ä4
, ä8
, ä10
, (4)
ä2
, ä7
, ä8
, ä4
, ä3
, (5)
ä10
, ä7
, ä4
, ä8
, ä7
, ä2
. (6)
в графе, изображенном на рис. 2.1.2, являются маршрутами; две точки над эмблемой дуги означают, что ее ориентацией третируют, т.е. дуга рассматривается как неориентированное ребро. Также путь либо маршрут можно изображать последовательностью вершин. к примеру, путь (1) будет смотреться последующем образом: х2
, х5
, х4
, х3
, х5
, х6
. время от времени дугам графа приписываются числа, называемыевесом, стоимостью, либо длиной данной нам дуги. В этом случае граф именуется графом с взвешенными дугами.
А если вес приписывается верхушкам графа, то тогда выходит граф с взвешенными верхушками. Если в графе веса приписаны и дугам и верхушкам, то он именуется просто взвешенным.
При рассмотрении пути µ представленного последовательностью дуг (ä1
, ä2
,…, äq
), за его вес принимается число l(µ), равное сумме весов всех дуг, входящих в µ, т.е.

2.2 метод Дейкстры
Метод Дейкстры строит кратчайшие пути, ведущие из начальной верхушки графа к остальным верхушкам этого графа (если таковые имеются).
В процессе работы метода поочередно помечаются рассмотренные верхушки графа. При этом верхушка, помеченная крайней (на данный момент) размещена поближе к начальной верхушке, чем все непомеченные, но далее, чем все помеченные.
Поначалу помечается начальная верхушка; последующей, разумеется, будет помечена верхушка, наиблежайшая к начальной, и смежная с ней.
Пусть на каком-то шаге уже помечено несколько вершин. Известны кратчайшие пути, ведущие из начальной верхушки к помеченным. Для каждой из непомеченных вершин проделаем последующее:
1. Разглядим все дуги, ведущие из помеченных вершин в одну непомеченную. Любая таковая дуга является крайней дугой на пути из начальной верхушки в эту непомеченную.
2. Выберем из этих путей кратчайший. А потом выберем посреди их самый маленький ко всем непомеченным верхушкам, и пометим верхушку, к которой он ведет.
метод закончится, когда будут помечены все достижимые верхушки.
В итоге работы метода Дейкстры строится Дерево кратчайших путей.
3 ОСОБЕННОСТИ работы В СРЕДЕ
При написании программки использовалась среда Microsoft Visual C++ 6.0. Данная среда дозволяет писать приложения на языке C++.
В процессе написания программки все операторы и служебные слова языка С++ выделяются остальным цветом, чтоб различать их от переменных, данных программером. Среда Microsoft Visual C++ 6.0 содержит интегрированный компилятор.
Окно программки разбито на несколько частей. Вверху находится обычная панель – Standart, с которой можно сохранить начальный текст программки на диск, открыть новейший документ, скопировать либо вставить текст, отменить крайнее действие, либо отыскать текст. Слева находятся панели ObjectTreeView и ObjectInspector, на которых показаны объекты, которые употребляются в данной программке, и их характеристики. В центре окна программки размещен текстовый редактор, в каком следует писать программку. Понизу – панель Output, в какой показывается сообщения, если в программке содержатся ошибки – компилятор докладывает вид ошибки и строчку, в какой она допущена, довольно создать двойной кликлевой клавишеймыши на описании ошибки в Output, чтобыпереместиться на строчку, содержащую ошибки.
программка сотворена в консольном режиме – в режиме, не имеющем графического интерфейса.
4 ПРОГРАММНАЯ РЕАЛИЗАЦИЯ
4.1 Описание метода и структуры программки
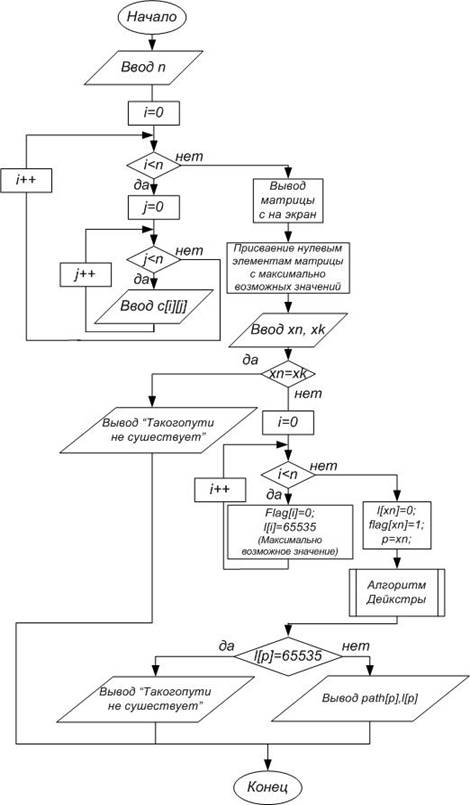
Рис. 4.1.1
программка выводит малый путь меж 2-мя обозначенными верхушками в графе и его длину.
При запуске программки на экран выводится запрос о вводе весов рёбер исследуемого графа. Данные, введённые юзером, показываются в виде матрицы смежности, в какой не имеющиеся рёбра обозначаются нулями. Опосля обозначенным рёбрам присваивается
Последующим шагом выполнения программки является запрос о вводе номеров вершин, меж которыми нужно выяснить путь. В случае, если исходная и конечная верхушки совпадают, отображается соответственное сообщение и работа программки заканчивается. В неприятном случае производится конкретно метод Дейкстры, схема которого приведена в приложении В.
Результатом программки является вывод на экран вершин, через которые проходит малый путь, также вывод длины маршрута. Если пути меж данными точками не существует – выводится соответственное сообщение.
4.2 Описание использованных программных средств
Таблица 4.2.1–Описание переменных
Переменная
Тип
Описание
n
int
количество точек (вершин) грифа
i,j
int
Счётчики
p
int
Номер кратчайшего пути и меньшей длины пути
xn
int
Номер исходной точки (верхушки)
xk
int
Номер конечной точки (верхушки)
flag[11]
int
Массив, i-й элемент которого имеет Word (unsigned int)
Массив i-j элемент которого содержит расстояние меж i-й и j-й точками (верхушками)
Замечание:
1. с[i][i]=¥
2. c[i][j]=c[j][i]
s[80]
char
Строчная переменная, которая содержит промежные значения пути
path[80][11]
char
Массив строк, который содержит пути
Замечание:
Опосля прохождения обработки по методу Дейкстры p-й элемент массива содержит кратчайший путь.
l[11]
Word (unsigned int)
Массив, который содержит длины путей (Path)
Замечание:
Опосля прохождения обработки по методу Дейкстры p-й элемент массива содержит длину кратчайшего пути.
Не считая обычных функций из библиотек iostream.h, string.h, stdio.h, conio.h были применены также последующие функции.
· wordminim(wordx, wordy) – функция, которая возвращает малое из x и y.

Рис. 4.2.1
· intmin(intn) – функция, которая возвращает номер элемента массива l[i] малой «неотмеченной» длиной пути(flag[i]=0).

Рис. 4.2.2
5 ИНСТРУКЦИЯ ПОЛЬЗОВАТЕЛЯ
При запуске программки на дисплее покажется окно с инструкциями. Делайте эти аннотации, а конкретно:
1.Введите количество вершин исследуемого графа.
2.Введите веса рёбер (положительное число). В программке расстояния от хi
до xi
+1
и xi
+1
до хi
числятся равными, а расстояния от хi
до хi
– не существующими. Если ребра меж обозначенными верхушками не существует, введите 0 (ноль).
На экран выводится матрица смежности, отображающая введённую информацию.
3.Введите номер верхушки, от которой начинается разыскиваемый путь.
4.Введите номер верхушки, в какой путь завершается.
5.Чтобы окончить работу программки опосля получения результата нажмите Enter.
ЗАКЛЮЧЕНИЕ
Таковым образом, в процессе сотворения данного проекта разработана программка, реализующая метод Дейкстры в Microsoft Visual C++ 6.0. Её недочетом является простой пользовательский интерфейс. Это соединено с тем, что программка работает в консольном режиме, не добавляющем к трудности языка сложность программного оконного интерфейса
Также были углублены познания, приобретенные в процессе выполнения лабораторных работ по предмету «Программирование».
ПЕРЕЧЕНЬ ССЫЛОК
1.Бондарев В.М. Программирование на С++.–Х: «Компания СМИТ», 2004
2.Страуструп Бьярн язык программирования С++(2 ч).–«К:ДиаСофт», 1993
3.Хаханов В.И., Чумаченко С.В. Дискретная математика (теоретическое и практическое содержание курса).–Кафедра АПВТ, 2002
4.метод Дейкстры
5.Конспект лекций.
приложение А
Текст программки
#include<iostream.h>
#include<string.h>
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
#define Word unsigned int
int i, j, n, p, xn, xk;
int flag[11];
word c[11][11], l[11];
char s[80], Path[80][11];
int min(int n)
{
int i, result;
for(i=0;i<n;i++)
if(!(flag[i])) result=i;
for(i=0;i<n;i++)
if((l[result]>l[i])&&(!flag[i])) result=i;
return result;
}
Word minim(word x, word y)
{
if(x<y) return x;
return y;
}
void main()
{
cout<<«Vvedite kolichestvo tochek: «;
cin>>n;
for(i=0;i<n;i++)
for(j=0;j<n;j++) c[i][j]=0;
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
{
cout<<«Vvedite rasstoyanie ot x»<<i+1<<» do x»<<j+1<<«: «;
cin>>c[i][j];
}
cout<<» «;
for(i=0;i<n;i++) cout<<» X»<<i+1;
cout<<endl<<endl;
for(i=0;i<n;i++)
{
printf(«X%d»,i+1);
for(j=0;j<n;j++)
{
printf(«%6d»,c[i][j]);
c[j][i]=c[i][j];
}
printf(«nn»);
}
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(c[i][j]==0) c[i][j]=65535; //бесконечность
cout<<«Vvedite nachalnuy tochku: «;
cin>>xn;
cout<<«Vvedite konechnuy tochku: «;
cin>>xk;
xk—;
xn--;
if(xn==xk)
{
cout<<«Nachalnaya I konechnaya tochki sovpadayt.»<<endl;
getch();
return;
}
for(i=0;i<n;i++)
{
flag[i]=0;
l[i]=65535;
}
l[xn]=0;
flag[xn]=1;
p=xn;
itoa(xn+1,s,10);
for(i=1;i<=n;i++)
{
strcpy(Path[i],»X»);
strcat(path[i],s);
}
do
{
for(i=0;i<n;i++)
if((c[p][i]!=65535)&&(!flag[i])&&(i!=p))
{
if(l[i]>l[p]+c[p][i])
{
itoa(i+1,s,10);
strcpy(Path[i+1],path[p+1]);
strcat(path[i+1],»-X»);
strcat(Path[i+1],s);
}
l[i]=minim(l[i],l[p]+c[p][i]);
}
p=min(n);
flag[p]=1;
}
while(p!=xk);
if(l[p]!=65535)
{
cout<<«Put: «<<Path[p+1]<<endl;
cout<<«Dlina puti: «<<l[p]<<endl;
}
else
cout<<«takogo puti ne syshestvuet!»<<endl;
getch();
}
приложение Б
Итог

Приложение В
Схема программной реализации метода Дейкстры
 ]]>
]]>

 (5 оценок, среднее: 4,80 из 5)
(5 оценок, среднее: 4,80 из 5)