Учебная работа. Курсовая работа: Транспортная задача линейного программирования

Калининградский филиал
Специальность-Менеджмент
1.История зарождения и сотворения линейного программирования.
Любой человек раз в день, не постоянно осознавая это, решает делему: как получить больший эффект, владея ограниченными средствами. Наши средства и ресурсы постоянно ограничены. Жизнь была бы наименее увлекательной, если б это было не так. Не тяжело выиграть схватка, имея армию в 10 раз огромную, чем у противника. Чтоб достигнуть большего эффекта, имея ограниченные средства, нужно составить план, либо программку действий. Ранее план в таковых вариантах составлялся “приблизительно” (сейчас, вообщем, часто тоже). Посреди XX века был сотворен особый математический аппарат, помогающий это созодать “по науке”. Соответственный раздел арифметики именуется математическим программированием. слово “программирование” тут и в подобных определениях (“линейное программирование, динамическое программирование” и т.п.) должно частично историческому недоразумению, частично неточному переводу с британского. По-русски лучше было бы употребить слово “планирование”. С программированием для ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) математическое программирование имеет только то общее, что большая часть возникающих на практике задач математического программирования очень громоздки для ручного счета, решить их можно лишь при помощи ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач), за ранее составив программку. временем рождения линейного программирования принято считать 1939г., когда была написана брошюра Леонида Витальевича Канторовича “Математические способы организации и планирования производства”. Так как способы, изложенные Л.В.Канторовичем, были не достаточно подходящи для ручного счета, а быстродействующих вычислительных машин в то время не было, работа Л.В.Канторовича осталась практически не увиденной.
Свое 2-ое рождение линейное программирование получило сначала 50-х годов с возникновением ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач). Тогда началось всеобщее увлечение линейным программированием, вызвавшее в свою очередь развитие остальных разделов математического программирования. В 1975 году академик Л.В.Канторович и янки доктор Т.Купманс получили Нобелевскую премию по экономическим наукам за “вклад в разработку теории и рационального использования ресурсов в экономике”.
В автобиографии, представленной в Нобелевский комитет, Леонид Витальевич Канторович ведает о событиях, случившихся в 1939 году. К нему, 26-летнему профессору-математику, обратились за консультацией сотрудники лаборатории планерного треста, которым необходимо было решить задачку о более удачном распределении материала меж станками. Эта задачка сводилась к нахождению максимума линейной функции, данной на полиэдре. Максимум таковой функции достигался в верхушке, но число вершин в данной для нас задачке достигало млрд. Потому обычной перебор вершин не годился. Леонид Витальевич писал: “оказалось, что эта задачка не является случайной. Я нашел огромное число различных по содержанию задач, имеющих аналогичный математический нрав: лучшее внедрение посевных площадей, выбор загрузки оборудования, оптимальный раскрой материала, распределение транспортных грузопотоков… Это напористо побудило меня к поиску действенного способа их решения”. И уже в летнюю пору 1939 года была сдана в набор книжка Л.В.Канторовича “Математические способы организации и планирования производства”, в какой закладывались основания того, что сейчас именуется математической экономикой.
Но идеи Л.В.Канторовича не повстречали осознания в момент их зарождения, были объявлены ложью, и его работа была прервана. Концепции Леонида Витальевича скоро опосля войны были переоткрыты на западе. Южноамериканский экономист Т.Купманс в течение почти всех лет завлекал внимание математиков к ряду задач, связанных с военной темой. Он интенсивно содействовал тому, чтоб был организован математический коллектив для разработки этих заморочек. В итоге было осознано, что нужно научиться решать задачки о нахождении экстремумов линейных функций на полиэдрах, задаваемых линейными неравенствами. По предложению Купманса этот раздел арифметики получил заглавие линейного программирования.
Южноамериканский математик А.Данциг в 1947 году разработал очень действенный определенный способ численного решения задач линейного программирования (он получил заглавие симплекс способа). Идеи линейного программирования в течение 5 6 лет получили потрясающее распространение в мире, и имена Купманса и Данцига стали всюду обширно известны.
Приблизительно в это время Купманс вызнал, что еще до войны в дальной Рф уже было изготовлено нечто схожее на разработку начал линейного программирования. Как просто было бы Данцигу и Купмансу проигнорировать эту информацию! Малая книжица, изданная жалким тиражом, обращенная даже не к экономистам, а к устроителям производства, с минимумом арифметики, без верно обрисованных алгоритмов, без доказательств теорем – словом, стоит принимать такую книгу во внимание… Но Купманс настаивает на переводе и издании на западе книжки Канторовича. Его имя и идеи стают известны всем. Воздадим подабающее благородству южноамериканского ученого!
А самому Леониду Витальевичу – как естественно было бы ему, испытав 1-ые суровые удары ретроградов, остеречься от “грехов” юности, запамятовать про всю эту экономику и возвратиться к арифметике. Но Л.В.Канторович продолжает писать математические работы, навеянные экономическими мыслями, участвует и в определенных разработках на производстве. При всем этом (сразу с Данцигом, но, не зная его работ) он разрабатывает способ, позднее нареченный симплекс-методом. Как в 50-е годы появляется небольшой просвет, и кое-что из запрещенного становится вероятным, он организует группу студентов на экономическом факультете ЛГУ для обучения способам рационального планирования. А, начиная с 1960 года, Леонид Витальевич занимается лишь экономической и связанной с нею математической неуввязками. Его вклад в данной для нас области был отмечен Ленинской премией в 1965 году (присуждена ему вместе с В.С.Немчиновым и В.В.Новожиловым) и, как уже говорилось, Нобелевской премией в 1975 году.
2.Транспортная задачка. Общая постановка, цели, задачки. Главные типы, виды моделей.
Под заглавием “транспортная задачка” соединяется воединыжды широкий круг задач с единой математической моделью. Данные задачки относятся к задачкам линейного программирования и могут быть решены симплексным способом. Но матрица системы ограничений транспортной задачки так своеобразна, что для ее решения разработаны особые способы. Эти способы, как и симплексный способ, разрешают отыскать изначальное опорное решение, а потом, улучшая его, получить наилучшее решение.
В общей постановке транспортная задачка состоит в отыскании оптимального плана перевозок некого однородного груза с 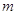 баз
баз 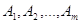
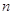 пользователям
пользователям 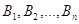 .
.
Различают два типа транспортных задач: но аспекту цены (план перевозок оптимален, если достигнут минимум издержек на его реализацию) и по аспекту времени (план оптимален, если на его реализацию затрачивается минимум времени).
(1.1)
Обозначим количество груза, имеющегося на каждой из 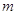 баз (припасы), соответственно
баз (припасы), соответственно 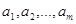 ,а общее количество имеющегося в наличии груза–
,а общее количество имеющегося в наличии груза–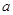 :
:
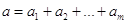 ;
;
(1.2)
заказы всякого из потребителей (потребности) обозначим соответственно , а полное количество потребностей –
, а полное количество потребностей – 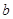 :
:
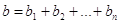 ,
,
(1.3)
Тогда при условии

(1.4)
мы имеем закрытую модель, а при условии

– открытую модель транспортной задачки.
Разумеется, в случае закрытой модели весь имеющийся в наличии груз развозится вполне, и все потребности заказчиков вполне удовлетворены; в случае же открытой модели или все заказчики удовлетворены и при всем этом на неких базах остаются избытки груза  , или весь груз оказывается израсходованным, хотя потребности вполне не удовлетворены
, или весь груз оказывается израсходованным, хотя потребности вполне не удовлетворены  .
.
Так же есть одноэтапные модели задач, где перевозка осуществляется впрямую от, к примеру, базы либо завода изготовителя к пользователю, и двухэтапные, где меж ними имеется “перевалочный пункт”, к примеру – склад.
План перевозок с указанием припасов и потребностей комфортно записывать в виде последующей таблицы, именуемой таблицей перевозок:
Пункты
Отправления
Пункты предназначения
Припасы

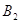
…
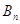
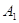
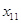

…
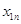

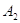
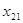
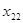
…
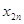

…
…
…
…
…
…
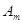
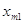
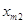
…

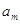
потребности
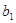
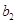
…


либо

Условие  либо
либо  значит, с какой задачей мы имеем дело, с закрытой моделью либо открытой моделью транспортной задачки. Переменное
значит, с какой задачей мы имеем дело, с закрытой моделью либо открытой моделью транспортной задачки. Переменное 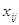 значит количество груза, перевозимого с базы
значит количество груза, перевозимого с базы 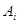 потребителю
потребителю 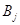 : совокупа этих величин образует матрицу (матрицу перевозок).
: совокупа этих величин образует матрицу (матрицу перевозок).
Разумеется, переменные 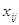 должны удовлетворять условиям:
должны удовлетворять условиям:
(2.1.1)
(2.1)

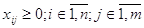
Система (2.1) содержит  уравнений с
уравнений с 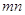 неведомыми. Её изюминка заключается в том, что коэффициенты при неведомых везде равны единице. Не считая того, все уравнения системы (2.1) могут быть разбиты на две группы: 1-ая группа из т первых уравнений (“горизонтальные” уравнения) и 2-ая группа из п других уравнений (“вертикальные” уравнения). В любом из горизонтальных уравнений содержатся неведомые с одним и этим же первым индексом (они образуют одну строчку матрицы перевозок), в любом из вертикальных уравнений содержатся неведомые с одним и этим же вторым индексом (они образуют один столбец матрицы перевозок). Таковым образом, любая неведомая встречается в системе (2.1) два раза: в одном и лишь одном горизонтальном и в одном и лишь одном вертикальном уравнениях.
неведомыми. Её изюминка заключается в том, что коэффициенты при неведомых везде равны единице. Не считая того, все уравнения системы (2.1) могут быть разбиты на две группы: 1-ая группа из т первых уравнений (“горизонтальные” уравнения) и 2-ая группа из п других уравнений (“вертикальные” уравнения). В любом из горизонтальных уравнений содержатся неведомые с одним и этим же первым индексом (они образуют одну строчку матрицы перевозок), в любом из вертикальных уравнений содержатся неведомые с одним и этим же вторым индексом (они образуют один столбец матрицы перевозок). Таковым образом, любая неведомая встречается в системе (2.1) два раза: в одном и лишь одном горизонтальном и в одном и лишь одном вертикальном уравнениях.
 Таковая структура системы (2.1) дозволяет просто установить ее ранг. Вправду, покажем, что совокупа неведомых, образующих первую строчку и 1-ый столбец матрицы перевозок, можно принять в качестве базиса. При таком выборе базиса, по последней мере, один из 2-ух их индексов равен единице, а, следовательно, вольные неведомые определяются условием
Таковая структура системы (2.1) дозволяет просто установить ее ранг. Вправду, покажем, что совокупа неведомых, образующих первую строчку и 1-ый столбец матрицы перевозок, можно принять в качестве базиса. При таком выборе базиса, по последней мере, один из 2-ух их индексов равен единице, а, следовательно, вольные неведомые определяются условием 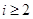 ,
, 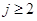 .Перепишем систему (2.1) в виде
.Перепишем систему (2.1) в виде
(2.1’)
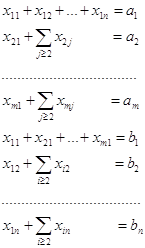
где знаки 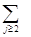 и
и 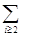 означают суммирование по соответственному индексу. Так, к примеру,
означают суммирование по соответственному индексу. Так, к примеру,

При всем этом просто увидеть, что под знаками такового суммирования соединяются воединыжды лишь вольные неведомые (тут 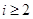 ,
, 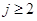 ).
).
В рассматриваемой нами системе лишь два уравнения, а именно 1-ое горизонтальное и 1-ое вертикальное, содержат наиболее 1-го неведомого из числа избранных нами для построения базиса. Исключив из первого горизонтального уравнения базовые неведомые  при помощи вертикальных уравнений, мы получаем уравнение
при помощи вертикальных уравнений, мы получаем уравнение

либо короче
(2.2)

где знак  значит сумму всех вольных неведомых. Аналогично, исключив из первого вертикального уравнения базовые неведомые
значит сумму всех вольных неведомых. Аналогично, исключив из первого вертикального уравнения базовые неведомые  при помощи горизонтальных уравнений, мы получаем уравнение
при помощи горизонтальных уравнений, мы получаем уравнение
(2.2’)

Потому что для закрытой модели транспортной задачки  , то приобретенные нами уравнения (2.2) и (2.2’) схожи и, исключив из 1-го из их неведомое
, то приобретенные нами уравнения (2.2) и (2.2’) схожи и, исключив из 1-го из их неведомое 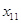 , мы получим уравнение-тождество 0=0, которое из системы вычеркивается.
, мы получим уравнение-тождество 0=0, которое из системы вычеркивается.
 Итак, преобразование системы (2.1) свелось к подмене 2-ух уравнений (первого горизонтального и первого вертикального) уравнением (2.2). Другие уравнения остаются постоянными. Система приняла вид
Итак, преобразование системы (2.1) свелось к подмене 2-ух уравнений (первого горизонтального и первого вертикального) уравнением (2.2). Другие уравнения остаются постоянными. Система приняла вид
(2.3)

В системе (2.3) выделен обозначенный выше базис: базовые неизвестные из первых т уравнений образуют 1-ый столбец матрицы перевозок, а базовые неведомые других уравнений образуют первую строчку матрицы перевозок без первого неведомого 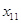 [она заходит в 1-ое уравнение системы (2.3)]. В системе (2.3) имеется
[она заходит в 1-ое уравнение системы (2.3)]. В системе (2.3) имеется  уравнений, выделенный базис содержит
уравнений, выделенный базис содержит  неизвестных, а, как следует, и ранг системы (2.1)
неизвестных, а, как следует, и ранг системы (2.1)  .
.
Для решения транспортной задачки нужно не считая припасов и потребностей знать также и тарифы  , т. е. стоимость перевозки единицы груза с базы
, т. е. стоимость перевозки единицы груза с базы 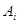 пользователю
пользователю 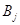 .
.
совокупа тарифов  также образует матрицу, которую можно соединить с матрицей перевозок и данными о припасах и потребностях в одну таблицу:
также образует матрицу, которую можно соединить с матрицей перевозок и данными о припасах и потребностях в одну таблицу:
Пункты
Отправления
Пункты предназначения
Припасы

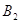
…
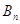
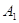


…


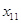

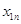
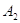


…


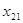
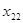
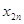
…
…
…
…
…
…
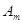


…

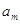
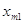
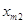

потребности
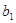
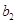
…


либо

Сумма всех издержек, т. е. стоимость реализации данного плана перевозок, является линейной функцией переменных 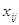 :
:
(2.4)

Требуется в области допустимых решений системы уравнений (2.1) и (2.1.1) отыскать решение, минимизирующее линейную функцию (2.4).
Таковым образом, мы лицезреем, что транспортная задачка является задачей линейного программирования. Для ее решения используют также симплекс-способ, но в силу специфичности задачки тут возможно обойтись без симплекс-таблиц. Решение можно получить методом некоторых преобразований таблицы перевозок. Эти преобразования соответствуют переходу от 1-го плана перевозок к другому. Но, как и в общем случае, наилучшее решение ищется посреди базовых решений. Как следует, мы будем иметь дело лишь с базовыми (либо опорными) планами. Потому что в данном случае ранг системы ограничений-уравнений равен  то посреди всех
то посреди всех 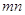 неизвестных
неизвестных 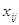 выделяется
выделяется  базовых неведомых, а другие
базовых неведомых, а другие  ·
·
неведомых являются вольными. В базисном решении вольные неведомые равны нулю. Обычно эти нули в таблицу не вчеркивают, оставляя надлежащие клеточки пустыми. Таковым образом, в таблице перевозок, представляющей опорный план, мы имеем  заполненных и
заполненных и  ·
· пустых клеток.
пустых клеток.
Для контроля нужно инспектировать, равна ли сумма чисел в заполненных клеточках каждой строчки таблицы перевозок припасу груза на соответственной базе, а в любом столбце — потребности заказчика [сиим подтверждается, что данный план является решением системы (2.1)].
Замечание 1. Не исключаются тут и вырожденные случаи, т. е. возможность воззвания в нуль одной либо нескольких базовых неведомых. Но эти нули в отличие от нулей вольных неизвестных вписываются в подобающую клеточку, и эта клеточка считается заполненной.
Замечание 2. Под величинами  , разумеется, не непременно подразумевать лишь тарифы. Можно также считать их величинами, пропорциональными тарифам, к примеру, расстояниями от баз до потребителей. Если, к примеру,
, разумеется, не непременно подразумевать лишь тарифы. Можно также считать их величинами, пропорциональными тарифам, к примеру, расстояниями от баз до потребителей. Если, к примеру, 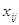 выражены в тоннах, а
выражены в тоннах, а  в километрах, то величина
в километрах, то величина  , определяемая формулой (2.4), является количеством тонно-километров, составляющих размер данного плана перевозок. Разумеется, что Издержки на перевозки пропорциональны количеству тонно-километров и, как следует, будут минимальными при минимуме S. В этом случае заместо матрицы тарифов мы имеем матрицу расстояний.
, определяемая формулой (2.4), является количеством тонно-километров, составляющих размер данного плана перевозок. Разумеется, что Издержки на перевозки пропорциональны количеству тонно-километров и, как следует, будут минимальными при минимуме S. В этом случае заместо матрицы тарифов мы имеем матрицу расстояний.
3. способы составления исходного опорного плана.
Как и в общем случае, решение транспортной задачки начинается с отыскания первого опорного плана (начального базиса). Мы рассмотрим два более всераспространенных способа построения такового базиса. Сущность обоих этих способов заключается в том, что базовый план составляется последовательно, в несколько шагов (поточнее,  шагов). На любом из этих шагов заполняется одна клеточка, притом так, что, или полностью удовлетворяется один из заказчиков (тот, в столбце которого находится заполняемая клеточка), или вполне вывозится весь припас груза с одной из баз (с той, в строке которой находится заполняемая клеточка).
шагов). На любом из этих шагов заполняется одна клеточка, притом так, что, или полностью удовлетворяется один из заказчиков (тот, в столбце которого находится заполняемая клеточка), или вполне вывозится весь припас груза с одной из баз (с той, в строке которой находится заполняемая клеточка).
В первом случае мы можем исключить столбец, содержащий заполненную на этом шаге клеточку, и считать, что задачка свелась к наполнению таблицы с числом столбцов, на единицу наименьшим, чем было перед сиим шагом, но с этим же количеством строк и с соответственно модифицированным припасом груза на одной из баз (на той базе, которой был удовлетворен заказчик на данном шаге).
Во 2-м случае исключается строчка, содержащая заполняемую клеточку, и считается, что таблица сузилась на одну строчку при постоянном количестве столбцов и при соответственном изменении потребности заказчика, в столбце которого находится заполняемая клеточка.
Начиная с сначало данной таблицы и повторив  раз описанный шаг, мы придем к “таблице”, состоящей из одной строчки и 1-го столбца (по другому говоря, из одной пустой клеточки). Иными словами, мы пришли к задачке с одной базой и с одним пользователем, при этом потребности этого единственного заказчика равны припасу груза на данной для нас единственной базе. Заполнив последнюю клеточку, мы освобождаем последнюю базу и удовлетворяем потребность крайнего заказчика. В итоге, совершив
раз описанный шаг, мы придем к “таблице”, состоящей из одной строчки и 1-го столбца (по другому говоря, из одной пустой клеточки). Иными словами, мы пришли к задачке с одной базой и с одним пользователем, при этом потребности этого единственного заказчика равны припасу груза на данной для нас единственной базе. Заполнив последнюю клеточку, мы освобождаем последнюю базу и удовлетворяем потребность крайнего заказчика. В итоге, совершив  шагов, мы и получим разыскиваемый опорный план.
шагов, мы и получим разыскиваемый опорный план.
Замечание. Может случиться, что уже на неком (но не на крайнем!) шаге Потребность еще одного заказчика окажется равной припасу груза на очередной базе. Тогда опосля наполнения очередной клеточки размер таблицы вроде бы сразу миниатюризируется на одни столбец и на одну строчку. Да и при всем этом мы должны считать, что уменьшение размера таблицы происходит или на один столбец, а на базе сохраняется “остаток” равный нулю, или на одну строчку, а у заказчика еще осталась неудовлетворенная “потребность” в количестве нуля единиц груза, которая и удовлетворяется на одном из последующих шагов. Этот нуль (“припас” либо “потребностью” – индифферентно) нужно записать в еще одну заполняемую клеточку на одном из следующих шагов. Потому что при всем этом оказывается равной нулю одна из базовых неведомых, то мы имеем дело с вырожденным случаем.
Различие способов отыскания первого опорного плана состоит в различии методов набора заполняемой клеточки.
1.Диагональный способ, либо способ северо-западного угла. При всем этом способе на любом шаге построения первого опорного плана заполняется левая верхняя клеточка (северо-западный угол) оставшейся части таблицы. При таком способе наполнение таблицы начинается с клеточки неведомого 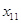 и завершается в клеточке неизвестного
и завершается в клеточке неизвестного  , т. е. идет вроде бы на искосок таблицы перевозок.
, т. е. идет вроде бы на искосок таблицы перевозок.
Пример.
Пункты
Отправления
Пункты предназначения
Припасы

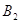



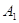
70
50
15
80
70
300
170
110
20
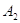
80
90
40
60
85
150
80
70

50
10
90
11
25
250
50
200
потребности
170
110
100
120
200
700
Наполнение таблицы начинается с ее северо-западного угла, т. е. клеточки с неведомым 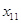 . 1-ая база
. 1-ая база 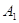 может вполне удовлетворить потребность первого заказчика
может вполне удовлетворить потребность первого заказчика 
 . Полагая
. Полагая  , вписываем это и исключаем из рассмотрения 1-ый столбец. На базе
, вписываем это и исключаем из рассмотрения 1-ый столбец. На базе 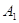 остается модифицированный припас
остается модифицированный припас  . В оставшейся новейшей таблице с 3-мя строчками
. В оставшейся новейшей таблице с 3-мя строчками  и 4-мя столбцами
и 4-мя столбцами  ; северо-западным углом будет клеточка для неведомого
; северо-западным углом будет клеточка для неведомого  . 1-ая база с припасом
. 1-ая база с припасом  может вполне удовлетворить потребность второго заказчика
может вполне удовлетворить потребность второго заказчика 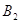
 . Полагаем
. Полагаем  , вписываем это значение в клеточку
, вписываем это значение в клеточку  и исключаем из рассмотрения 2-ой столбец. На базе
и исключаем из рассмотрения 2-ой столбец. На базе 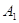 остается новейший остаток (припас)
остается новейший остаток (припас)  . В оставшейся новейшей таблице с 3-мя строчками
. В оставшейся новейшей таблице с 3-мя строчками  и 3-мя столбцами
и 3-мя столбцами  северо-западным углом будет клеточка для неведомого
северо-западным углом будет клеточка для неведомого  . сейчас 3-ий заказчик
. сейчас 3-ий заказчик  может принять весь припас с базы
может принять весь припас с базы 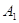
 . Полагаем
. Полагаем  , вписываем это и исключаем из рассмотрения первую строчку. У заказчика из
, вписываем это и исключаем из рассмотрения первую строчку. У заказчика из  осталась еще не довольной Потребность
осталась еще не довольной Потребность  .
.
Сейчас перебегаем к наполнению клеточки для неведомого  и т.д.
и т.д.
Через 6 шагов у нас остается одна база  с припасом груза (остатком от предшествующего шага)
с припасом груза (остатком от предшествующего шага)  и один пункт
и один пункт  с потребностью
с потребностью . Соответственно этому имеется одна вольная клеточка, которую и заполняем, положив
. Соответственно этому имеется одна вольная клеточка, которую и заполняем, положив  . План составлен. Базис образован неведомыми
. План составлен. Базис образован неведомыми  . Правильность составленного плана просто проверить, подсчитав суммы чисел, стоящих в заполненных клеточках по строчкам и столбцам.
. Правильность составленного плана просто проверить, подсчитав суммы чисел, стоящих в заполненных клеточках по строчкам и столбцам.
Общий размер перевозок в тонно-километрах для этого плана составит
 .
.
2.способ меньшей цены. При всем этом способе на любом шаге построения опорного плана первою заполняется та клеточка оставшейся части таблицы, которая имеет меньший тариф. Если таковая клеточка не единственная, то заполняется неважно какая из их.
Пример.
Пункты
Отправления
Пункты предназначения
Припасы

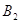



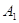
70
50
15
80
70
300
20
100
180
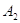
80
90
40
60
85
150
150

50
10
90
11
25
250
110
120
20
потребности
170
110
100
120
200
700
В этом случае наполнение таблицы начинается с клеточки для неизвестного  , для которого мы имеем , наименьше из всех значений
, для которого мы имеем , наименьше из всех значений  . Эта клеточка находится на пересечении третьей строчки и второго столбца, подходящим третьей базе
. Эта клеточка находится на пересечении третьей строчки и второго столбца, подходящим третьей базе  и второму заказчику
и второму заказчику 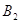 . 3-я база
. 3-я база  может вполне удовлетворить потребность второго заказчика
может вполне удовлетворить потребность второго заказчика 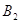
 . Полагая
. Полагая  , вписываем это и исключаем из рассмотрения 2-ой столбец. На базе
, вписываем это и исключаем из рассмотрения 2-ой столбец. На базе  остается изменённый припас
остается изменённый припас  . В оставшейся новейшей таблице с 3-мя строчками
. В оставшейся новейшей таблице с 3-мя строчками  и 4-мя столбцами
и 4-мя столбцами  клеточкой с минимальным значением
клеточкой с минимальным значением  клеточка, где
клеточка, где . Заполняем описанным выше методом эту клеточку и аналогично заполняем последующие клеточки. В результате оказываются заполненными (в приведенной последовательности) последующие клеточки:
. Заполняем описанным выше методом эту клеточку и аналогично заполняем последующие клеточки. В результате оказываются заполненными (в приведенной последовательности) последующие клеточки:
 .
.
На 5-ом шаге клеток с меньшими значениями  оказалось две
оказалось две  . Мы заполнили клеточку для
. Мы заполнили клеточку для  , положив
, положив  . Можно было избрать для наполнения другую клеточку, положив
. Можно было избрать для наполнения другую клеточку, положив  , что приведет в итоге к другому опорному плану. Общий размер перевозок в тонно-километрах для этого плана составит
, что приведет в итоге к другому опорному плану. Общий размер перевозок в тонно-километрах для этого плана составит
 .
.
Замечание. В диагональном способе не учитываются величины тарифов, в способе же меньшей цены эти величины учитываются, и нередко крайний способ приводит к плану с наименьшими общими затратами (что и имеет пространство в нашем примере), хотя это и не непременно.
Не считая рассмотренных выше методов время от времени употребляется, так именуемый, способ Фогеля. Сущность его состоит в последующем: В распределительной таблице по строчкам и столбцам определяется разность меж 2-мя меньшими тарифами. Отмечается большая разность. Дальше в строке (столбце) с большей разностью заполняется клеточка с минимальным тарифом. Строчки (столбцы) с нулевым остатком груза в предстоящем в расчет не принимаются. На любом шаге загружается лишь одна клеточка. Распределение груза делается, как и ранее.
4.понятие потенциала и цикла.
Для перехода от 1-го базиса к другому при решении транспортной задачки употребляются так именуемые циклы.
Циклом пересчета либо короче, циклом в таблице перевозок именуется последовательность неведомых, удовлетворяющая последующим условиям:
Одно из неведомых последовательности свободное, а все другие – базовые.
Любые два примыкающих в последовательности неведомых лежат или в одном столбце, или в одной строке.
Три поочередных неведомых не могут находиться в одном столбце либо в одной строке.
Если, начиная с какого-нибудь неведомого, мы будем поочередно перебегать от 1-го к последующему за ним неведомому то, через несколько шагов мы вернемся к начальному неведомому.
2-ое условие значит, что у 2-ух примыкающих неведомых в цикле или 1-ые, или 2-ые индексы схожи.
Если любые два примыкающих неведомых цикла соединить отрезком прямой, то будет получено геометрическое изображение цикла – замкнутая ломаная из чередующихся горизонтальных и вертикальных звеньев, одна из вершин которой находится в вольной клеточке, а другие — в базовых клеточках.
Можно обосновать, что для хоть какой вольной клеточки таблицы перевозок существует один и лишь один цикл, содержащий свободное неведомое из данной для нас клеточки, и что число вершин в цикле постоянно четно.
Так, к примеру, в таблице перевозок, составленной по диагональному способу при решения задачки из предшествующего пт, неведомому 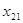 соответствует цикл
соответствует цикл  и т.д.
и т.д.
Пусть сейчас мы имеем некую вольную клеточку с подходящим ей циклом. Если мы изменим , то, переходя поочередно от одной верхушки цикла к иной, мы должны будем в силу неизменности сумм по строчкам и по столбцам попеременно уменьшать и наращивать значения неведомых в цикле на то же число . к примеру, в обозначенном выше цикле для вольного неведомого
. к примеру, в обозначенном выше цикле для вольного неведомого 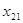 получим:
получим:
старенькые значения:  ;
;
новейшие значения: 
Разумеется, если снабдить верхушки цикла попеременно знаками “+” и “–“, приписав верхушке в вольной клеточке символ “+”, то можно сказать, что в верхушках со знаком “+” число  прибавляется к прежнему значению неведомого, находящегося в данной для нас верхушке, а в верхушках со знаком “–“ это число
прибавляется к прежнему значению неведомого, находящегося в данной для нас верхушке, а в верхушках со знаком “–“ это число  вычитается из прежнего значения неведомого, находящегося в данной для нас верхушке.
вычитается из прежнего значения неведомого, находящегося в данной для нас верхушке.
Замечание. Потому что число вершин в цикле постоянно четно, то, ворачиваясь в вольную клеточку, мы должны будем приписать ей символ “+”, т. е. тот символ, который ей уже приписан при выходе из нее. Это весьма существенное событие, потому что по другому мы пришли бы к противоречию. Индифферентно также, в котором направлении обходится цикл при “означивании” вершин.
Если в качестве  избрать меньшее из чисел, стоящих в верхушках, снабженных знаком “–“, то, по последней мере, одно из прежних базовых неведомых воспримет
избрать меньшее из чисел, стоящих в верхушках, снабженных знаком “–“, то, по последней мере, одно из прежних базовых неведомых воспримет
Так, к примеру, в рассмотренном выше цикле имеем отрицательные верхушки  и
и 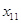 ; как следует, выбрав
; как следует, выбрав  , мы получаем:
, мы получаем:
старенькые значения:  ;
;
новейшие значения: 
т. е. заместо прежнего базового решения получаем новое базовое решение:
Пункты
Отправления
Пункты предназначения
Припасы

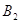



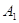
70
50
15
80
70
300
90
110
100
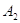
80
90
40
60
85
150
80
70

50
10
90
11
25
250
50
200
потребности
170
110
100
120
200
700
Выбор в качестве х малого посреди чисел, стоящих в отрицательных верхушках цикла, обеспечивает допустимость новейшего базиса.
Если малое одной отрицательной верхушке, то вольной оставляют лишь одну из их, а в остальных клеточках с этим же наименьшим значением пишут нули. В этом случае новое базовое решение будет вырожденным.
Может случиться, что и само малое значения всех неведомых при всем этом остаются постоянными, но решения числятся разными, потому что различны базисы. Оба решения вырождены.
Описанное выше преобразование таблицы перевозок, в итоге которого преобразуется базис, именуется пересчетом по циклу.
Заметим, что неведомые, не входящие в цикл, сиим преобразованием не затрагиваются, их значения остаются постоянными и каждое из их остается или в группе базовых, или в группе свободных неведомых, как и до пересчета.
Выясним сейчас, как пересчет по циклу влияет на общий размер издержек на перевозки и при каком условии эти Издержки стают меньше.
Пусть  – некое свободное неведомое, для которого мы выстроили цикл и выполнили пересчет по циклу с неким числом
– некое свободное неведомое, для которого мы выстроили цикл и выполнили пересчет по циклу с неким числом  . Если верхушке цикла, находящейся в
. Если верхушке цикла, находящейся в  строке и
строке и  столбце таблицы перевозок, приписан символ “+”, то , находящегося в данной для нас верхушке, возрастает на
столбце таблицы перевозок, приписан символ “+”, то , находящегося в данной для нас верхушке, возрастает на  , что в свою очередь вызывает повышение издержек на
, что в свою очередь вызывает повышение издержек на  . где
. где  – тариф, соответственный данной для нас клеточке; если же обозначенной верхушке приписан символ “–”, то миниатюризируется на
– тариф, соответственный данной для нас клеточке; если же обозначенной верхушке приписан символ “–”, то миниатюризируется на  , что вызывает уменьшение издержек на
, что вызывает уменьшение издержек на  .
.
Сложим тарифы, надлежащие положительным верхушкам цикла, и вычтем из данной для нас суммы сумму тарифов, соответственных отрицательным верхушкам цикла; полученную разность  назовем алгебраической суммой тарифов для данного вольного неведомого
назовем алгебраической суммой тарифов для данного вольного неведомого  . Подсчет алгебраической суммы тарифов можно объяснить и так: припишем тарифам те же знаки, которые приписаны подходящим верхушкам цикла, тогда алгебраическая сумма тарифов равна сумме таковых тарифов со знаком (“относительных тарифов”).
. Подсчет алгебраической суммы тарифов можно объяснить и так: припишем тарифам те же знаки, которые приписаны подходящим верхушкам цикла, тогда алгебраическая сумма тарифов равна сумме таковых тарифов со знаком (“относительных тарифов”).
сейчас, разумеется, мы можем, заключить, что в целом при пересчете но циклу, соответственному вольному неведомому  общий размер издержек на перевозки поменяется на произведение алгебраической суммы тарифов на
общий размер издержек на перевозки поменяется на произведение алгебраической суммы тарифов на  , т. е. на величину
, т. е. на величину  . Как следует, если алгебраическая сумма тарифов для некого свободного неведомого
. Как следует, если алгебраическая сумма тарифов для некого свободного неведомого  отрицательна
отрицательна  , то пересчет по циклу, соответственному этому неведомому, приводит к уменьшению общей суммы издержек на реализацию плана перевозок. Если же алгебраическая сумма тарифов положительна
, то пересчет по циклу, соответственному этому неведомому, приводит к уменьшению общей суммы издержек на реализацию плана перевозок. Если же алгебраическая сумма тарифов положительна  , то пересчет по соответственному циклу приведет к повышению общей суммы издержек. И, в конце концов, если алгебраическая сумма тарифов равна нулю
, то пересчет по соответственному циклу приведет к повышению общей суммы издержек. И, в конце концов, если алгебраическая сумма тарифов равна нулю  , то пересчет по соответственному циклу не изменит общую сумму издержек (два разных базовых плана требуют схожих издержек на их реализацию).
, то пересчет по соответственному циклу не изменит общую сумму издержек (два разных базовых плана требуют схожих издержек на их реализацию).
Так, к примеру, для цикла  в рассмотренной задачке алгебраическая сумма тарифов
в рассмотренной задачке алгебраическая сумма тарифов
 .
.
означает, пересчет по этому циклу понижает расходы. И действительно, осуществив таковой пересчет, мы получаем план, по которому размер перевозок в тонно-километрах составляет

тогда как по начальному плану он составил  . Имеем понижение размера перевозок на 1200 тонно-километров, что и следовало ждать, потому что алгебраическая сумма тарифов в данном случае равна –15, а пересчет по циклу осуществляется при помощи числа
. Имеем понижение размера перевозок на 1200 тонно-километров, что и следовало ждать, потому что алгебраическая сумма тарифов в данном случае равна –15, а пересчет по циклу осуществляется при помощи числа  (изменение издержек равно
(изменение издержек равно  ).
).
Вычисление алгебраической суммы тарифов для всякого из свободных неведомых можно создавать без построения соответствующего цикла, пользуясь, так именуемыми, потенциалами. Припишем каждой базе 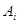 , некое число
, некое число  и любому пользователю
и любому пользователю 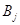 некое число
некое число  :
:
 ,
,
так что
(4.1)
 ,
,
где  – тарифы, надлежащие клеточкам, заполненным базисными неведомыми. Эти числа
– тарифы, надлежащие клеточкам, заполненным базисными неведомыми. Эти числа  и
и  именуются потенциалами соответственных баз и потребителей.
именуются потенциалами соответственных баз и потребителей.
Зная потенциалы, просто вычислить алгебраическую сумму тарифов. Вправду, если в алгебраической сумме тарифов по циклу, соответственному вольному неведомому  , поменять тарифы базовых клеток их выражениями через потенциалы по формулам (4.1), то, в силу чередования символов при верхушках цикла, все потенциалы, не считая
, поменять тарифы базовых клеток их выражениями через потенциалы по формулам (4.1), то, в силу чередования символов при верхушках цикла, все потенциалы, не считая  и
и  сократятся, и мы получим:
сократятся, и мы получим:
 .
.
Так, к примеру, для цикла  в рассмотренной выше задачке имеем
в рассмотренной выше задачке имеем
 .
.
Для базовых клеток сумма потенциалов строчки и столбца, в каких находится эта клеточка, равна тарифу, соответственному данной для нас клеточке; если же клеточка для неведомого  вольная, то сумму потенциалов
вольная, то сумму потенциалов
(4.2)

именуют косвенным тарифом данной для нас клеточки. Как следует, алгебраическая сумма тарифов для вольной клеточки  равна разности ее реального (“настоящего”) и косвенного тарифов:
равна разности ее реального (“настоящего”) и косвенного тарифов:
(4.3)

Из (4.3) следует, что если косвенный тариф для данной свободной клеточки больше её настоящего тарифа, то алгебраическая сумма тарифов по циклу, соответственному данной для нас клеточке, будет отрицательна; если же косвенный тариф меньше настоящего, то алгебраическая сумма тарифов положительна, и, в конце концов, если косвенный тариф равен настоящему, то алгебраическая сумма тарифов равна нулю.
Потенциалы можно отыскать из системы равенств (4.1), рассматривая их как систему  уравнений с
уравнений с  неведомыми. Потому что неведомых тут на единицу больше, чем уравнений, то, по последней мере, один из потенциалов мы можем избрать произвольно, положив, к примеру,
неведомыми. Потому что неведомых тут на единицу больше, чем уравнений, то, по последней мере, один из потенциалов мы можем избрать произвольно, положив, к примеру,  ; тогда другие потенциалы просто определяются из уравнений (4.1).
; тогда другие потенциалы просто определяются из уравнений (4.1).
к примеру, для плана, приобретенного по диагональному способу в рассмотренной выше задачке, имеем

Система содержит семь уравнений с восемью неведомыми. Выбирая произвольно , находим поочередно из первых 3-х уравнений значения  ,
,  ,
,  , потом из 4-ого уравнения –
, потом из 4-ого уравнения –  , из 5-ого уравнения –
, из 5-ого уравнения –  , из шестого уравнения
, из шестого уравнения  и, в конце концов, из седьмого уравнения –
и, в конце концов, из седьмого уравнения –  .
.
Положив, к примеру,  , получаем значения потенциалов:
, получаем значения потенциалов:


Найдем сейчас косвенные тарифы для вольных клеток и сравним их с настоящими тарифами:


Для клеток с неведомыми 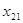 и
и  косвенные тарифы больше настоящих. Как следует, для их мы будем иметь отрицательные алгебраические суммы тарифов:
косвенные тарифы больше настоящих. Как следует, для их мы будем иметь отрицательные алгебраические суммы тарифов:

мы уже имели ранее, вычисляя алгебраическую сумму тарифов для данной для нас клеточки конкретно по циклу.
Замечание 1. Подсчитывая косвенные тарифы как суммы соответствующих потенциалов, полезно не пропускать и клеточки с базисными неведомыми (заполненные клеточки). Для этих клеток сумма потенциалов равна настоящему тарифу; крайнее может служить проверкой корректности отысканных значении потенциалов.
Замечание 2. Можно показать, что если сумму всех издержек по данному плану перевозок выразить через вольные неведомые [для этого надо исключить базисные неизвестные из выражения для S, см. формулу (2.4)], то коэффициент при любом из таковых неведомых будет равен алгебраической сумме тарифов по циклу, соответственному ей в таблице перевозок. Это снова подтверждает, что пересчет по циклам является специфичной формой внедрения симплекс-метода к решению транспортной задачки.
Аспект оптимальности базового решения транспортной задачки. Способы отыскания рационального решения.
Из произнесенного в прошлом пт вытекает последующий критерий оптимальности базового решения транспортной задачки: если для некого базового плана перевозок алгебраические суммы тарифов по циклам для всех вольных клеток неотрицательны, то этот план лучший.
Отсюда вытекает метод отыскания рационального решения транспортной задачки, состоящий в том, что, имея некое базисное решение, вычисляют алгебраические суммы тарифов для всех вольных клеток. Если аспект оптимальности выполнен, то данное решение является хорошим; если же имеются клеточки с отрицательными алгебраическими суммами тарифов, то перебегают к новенькому базису, производя пересчет по циклу, соответственному одной из таковых клеток. Приобретенное таковым образом новое базовое решение будет лучше начального – издержки на его реализацию будут наименьшими. Для новейшего решения также инспектируют выполнимость аспекта оптимальности и в случае необходимости опять совершают пересчет по циклу для одной из клеток с отрицательной алгебраической суммой тарифов и т. д.
Через конечное число шагов приходят к разыскиваемому хорошему базовому решению.
В случае если алгебраические суммы тарифов для всех свободных клеток положительны, мы имеем единственное наилучшее решение; если же алгебраические суммы тарифов для всех свободных клеток неотрицательны, но посреди их имеются алгебраические суммы тарифов, равные нулю, то наилучшее решение не единственное: при пересчете по циклу для клеточки с нулевой алгебраической суммой тарифов мы получим наилучшее же решение, но отличное от начального (Издержки по обоим планам будут одинаковыми).
Зависимо от способов подсчета алгебраических сумм тарифов для вольных клеток различают два способа отыскания оптимального решения транспортной задачки:
Распределительный способ. При всем этом способе для каждой пустой клеточки строят цикл и для всякого цикла конкретно вычисляют алгебраическую сумму тарифов.
способ потенциалов. При всем этом способе за ранее находят потенциалы баз и потребителей, а потом вычисляют для каждой пустой клеточки алгебраическую сумму тарифов при помощи потенциалов.
Достоинства способа потенциалов по сопоставлению с распределительным способом заключаются в том, что отпадает необходимость построения циклов для каждой из пустых клеток и упрощается вычисление алгебраических сумм тарифов. Цикл строится лишь один – тот, по которому делается пересчет.
Применяя способ потенциалов, можно гласить не о знаке алгебраических сумм тарифов, а о сопоставлении косвенных тарифов с настоящими. Требование неотрицательности алгебраических сумм тарифов заменяется условием, что косвенные тарифы не превосходят настоящих.
Следует подразумевать, что потенциалы (так же как и циклы) для всякого новейшего базового плана определяются поновой.
Выше рассматривалась закрытая модель транспортной задачки, с правильным балансом, когда производится условие (1.3). В случае выполнения (1.4) (открытая модель) баланс транспортной задачки может нарушаться в 2-ух направлениях:
1. Сумма припасов в пт отправления превосходит сумму поданных заявок (транспортная задачка с излишком припасов):
å аi > å bj ( где i=1,…,m ; j=1,…,n );
2. Сумма поданных заявок превосходит наличные припасы (транспортная задачка с излишком заявок):
å аi < å bj ( где i=1,…,m ; j=1,…,n );
Разглядим поочередно эти два варианта:
Транспортная задачка с излишком припасов.
Сведем её к ранее рассмотренной транспортной задачке с правильным балансом. Для этого, сверх имеющихся n пт предназначения В1, B2, … , Bn, введём ещё один, фиктивный, пункт предназначения Bn+1, которому припишем фиктивную заявку, равную излишку припасов над заявками
bn+1 = å аi — å bj ( где i=1,…,m ; j=1,…,n ) ,
а стоимость перевозок из всех пт отправления в фиктивный пункт предназначения bn+1 будем считать равной нулю. Введением фиктивного пт предназначения B n+1 с его заявкой b n+1 мы сравняли баланс транспортной задачки, и сейчас ее можно решать, как обыденную транспортную задачку с правильным балансом.
Транспортная задачка с излишком заявок.
Эту задачку можно свести к обыкновенной транспортной задачке с правильным балансом, если ввести фиктивный пункт отправления Am+1 с припасом am+1 равным недостающему припасу, и стоимость перевозок из фиктивного пт отправления во все пункты предназначения принять равной нулю.
задачка, двоякая к транспортной.
Построим задачку, двоякую к транспортной. С данной для нас целью вспомним, что любому пт отправления 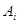 и предназначения
и предназначения 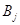 отвечает определенное ограничение
отвечает определенное ограничение
(6.1)

В то же время любому ограничению из (6.1) сопоставляется определенная неведомая в двойственной задачке. Тем устанавливается соответствие меж всеми пт 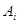 и
и 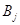 и всеми неизвестными двоякой задачки.
и всеми неизвестными двоякой задачки.
Обозначим неведомую в двоякой задачке, отвечающую пт отправления 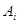 , через
, через  , а пт предназначения
, а пт предназначения 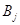 – через
– через  .
.
Любому неведомому в транспортной задачке соответствует ограничение, связывающее неведомые в двоякой задачке. Неведомое 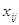 заходит ровно в два ограничения системы (6.1): одно из их отвечает пт
заходит ровно в два ограничения системы (6.1): одно из их отвечает пт 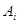 , а другое – пт
, а другое – пт 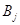 . В обоих этих уравнениях коэффициент при
. В обоих этих уравнениях коэффициент при 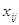 равен 1. Потому соответственное
равен 1. Потому соответственное 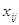 ограничение в двойственной задачке имеет вид
ограничение в двойственной задачке имеет вид
(6.2)

 .
.
Правая часть неравенства (6.2) равна  , поэтому что конкретно с сиим коэффициентом неведомая
, поэтому что конкретно с сиим коэффициентом неведомая 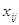 заходит в минимизируемую формулу (2.4).
заходит в минимизируемую формулу (2.4).
Оптимизируемая форма двоякой задачки имеет вид
(6.3)

Таковым образом, задачка двоякая к транспортной формулируется последующим образом. При ограничениях (6.2) максимизировать формулу (6.3). Подчеркнем, что символ значений неизвестных  и
и  быть может произвольным.
быть может произвольным.
Представим, что нам понятно некое допустимое базовое решение транспортной задачки, в каком все базисные неведомые строго положительны. Это решение нормально только в том случае, когда соответственная ей система оказывается совместной. Эта система возникает из системы (6.2), если в ней все неравенства, отвечающие базовым неведомым  поменять точными равенствами.
поменять точными равенствами.
В итоге приходим к соотношению:
(6.4)
 (для всех вольных неведомых
(для всех вольных неведомых 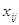 )
)
Тем мы убеждаемся, что признак оптимальности в работе по способу потенциалов совпадает с нужным и достаточным условием оптимальности.
7.Пример решения транспортной задачки.
В городке N имеется 4 склада Аi, на которых хранится тканей живых организмов изучает наука гистология). Ниже, в таблице, приведены данные по количеству рулонов на любом складе, запросы магазинов и стоимость перевозки 1-го рулона из Аi в Bj. нужно составить таковой план перевозок, при котором запросы магазинов будут удовлетворены при малой суммарной цены перевозок.
 магазины
магазины
Склад
B1
(b1=40)
B2
(b2=50)
B3
(b3=15)
B4
(b4=75)
B5
(b5=40)
А1 (а1=50)
1,0
2,0
3,0
2,5
3,5
А2(а2=20)
0,4
3,0
1,0
2,0
3,0
А3(а3=75)
0,7
1,0
1,0
0,8
1,5
А4(а4=80)
1,2
2,0
2,0
1,5
2,5
В данном случае Σai=225 >Σbj=220 => имеем дело с открытой моделью транспортной задачки. Сведем ее к закрытой введением фиктивного магазина B6 с потребностью b5=225-220=5 и стоимостью перевозок сi6=0.Имеем таблицу:
 магазины
магазины
Склад
B1
(b1=40)
B2
(b2=50)
B3
(b3=15)
B4
(b4=75)
B5
(b5=40)
B6
(b6=5)
А1 (а1=50)
1,0
2,0
3,0
2,5
3,5
0
А2(а2=20)
0,4
3,0
1,0
2,0
3,0
0
А3(а3=75)
0,7
1,0
1,0
0,8
1,5
0
А4(а4=80)
1,2
2,0
2,0
1,5
2,5
0
Математическая модель: обозначим xij – количество продукта, перевозимого из Аi в Bj. Тогда
 x11 x12 x13 x14 x15 x16
x11 x12 x13 x14 x15 x16
x21 x22 x23 x24 x25 x26
X = x31 x32 x33 x34 x35 x36 — матрица перевозок.
x41 x42 x43 x44 x45 x46
min(x11+2×12+3×13+2,5×14+3,5×15+0,4×21+3×22+x23+2×24+3×25+0,7×31+x32+x33+0,8×34+1,5×35++1,2×41+2×42+2×43+1,5×44+2,5×45) (1)
 x11+x12+x13+x14+x15+x16=50
x11+x12+x13+x14+x15+x16=50
x21+x22+x23+x24+x25+x26=20
x31+x32+x33+x34+x35+x36=75
x41+x42+x43+x44+x45+x46=80
x11+x21+x31+x41=40 (2)
x12+x22+x32+x42=50
x13+x23+x33+x43=15
x14+x24+x34+x44=75
x15+x25+x35+x45=40
x16+x26+x36+x46=5
xij≥0 (i=1,2,3,4 ; j=1,2,3,4,5,6 ) (3)
Двоякая ЗЛП:
max(50u1+20u2+75u3+80u4+40v1+50v2+15v3+75v4+40v5+5v6) (1*)

 u1+v1≤1
u1+v1≤1
u1+v2≤2
u1+v3≤3 (2*)
u1+v4≤2,5
u1+v5≤3,5
u1+v6≤0
ui,vj – произвольные (i=1,2,3,4 ; j=1,2,3,4,5,6 ) (3*)
Будем находить начальный план по способу меньшей цены:
1) x21=20 и 2-ую строчку исключаем.2) x31=20 и 1-ый столбец исключаем.
3) x34=55 и 3-ю строчку исключаем.4) x44=20 и 4-ый столбец исключаем.
5) x12=50 и 1-ю строчку и 2-ой столбец исключаем и x32=0. 6) x43=150 и 3-ий столбец исключаем.7) x45=40 и 5-ый столбец исключаем.x46=5.Составим таблицу. тут и дальше в нижнем правом углу записываем
 магазины
магазины
Склад
B1
(b1=40)
B2
(b2=50)
B3
(b3=15)
B4
(b4=75)
B5
(b5=40)
B6
(b6=5)
А1 (а1=50)
 1,0
1,0


50
2,0
 3,0
3,0
 2,5
2,5
 3,5
3,5
0
А2(а2=20)
 0,4
0,4
20
3,0
1,0
2,0
3,0
0
А3(а3=75)
 0,7
0,7
20
0
1,0
1,0
55
0,8
1,5
0
А4(а4=80)
1,2
2,0
15
2,0
20
1,5
40
2,5
5
0
Стоимость 1-ого плана:
D1=2•50+0,4•20+0,7•20+0,8•55+2•15+1,5•20+2,5•40=326.
Будем облагораживать этот план способом потенциалов: ui- потенциал Аi ,vj- потенциал Bj. Тогда u1+v2=2,u2+v1=0,4, u3+v1=0,7, u3+v2=1, u3+v4=0,8, u4+v3=2, u4+v4=1,5, u4+v5=2,5 ,u4+v6=0.Положим u1=0,тогда v2=2,u3=-1,v1=1,7,v4=1,8, u2=-1,3,u4=-0,3, v3=2,3,v5=2,8,v6=0,3.Составим таблицу:
 магазины
магазины
Склад
B1
(b1=40)
v1=1,7
B2
(b2=50)
v2=2
B3
(b3=15)
v3=2,3
B4
(b4=75)
v4=1,8
B5
(b5=40)
v5=2,8
B6
(b6=5)
v6=0,3

0,7
А1 (а1=50)
U1=0


0
1,0


— 0,7
50
2,0
— 0,7
3,0
— 0,7
2,5
0,3
3,5
0
0
А2(а2=20)
U2=-1,3
— 2,3
20
0,4
0
3,0
— 1,5
1,0
— 1,5
2,0
— 1
3,0
0
0
А3(а3=75)
U3=-1

0
0,7

20

0,3
0
1,0
0
1,0
0,3
55
0,8
— 0,7
1,5
0
0,2
А4(а4=80)
U4=-0,3
— 0,3
1,2
0
2,0
0
15
2,0
0
20
1,5
0
40
2,5
5
0
В верхнем левом углу тут и дальше записываем
u4+v1-c41 =0,2>0. => По аспекту оптимальности, 1-ый план не оптимален. Дальше max(0,7;0,3;0,3;0,3;0,2)=0,7. => Поместим перевозку в клеточку А1В1, сместив 20=min(20,50) по циклу, обозначенному в таблице штрихом. Получим новейшую таблицу. Найдем потенциалы: u1+v1=1,u1+v2=2,u2+v1=0,4,u3+v2=1, u3+v4=0,8, u4+v3=2, u4+v4=1,5, u4+v5=2,5 , u4+v6=0. Положим u1=0,тогда v1=1,u2=-0,6,v2=2,v4=1,8, u3=-1, u4=-0,3,v3=2,3,v5=2,8,v6=0,3. Составим таблицу:
 магазины
магазины
Склад
B1
(b1=40)
v1=1
B2
(b2=50)
v2=2
B3
(b3=15)
v3=2,3
B4
(b4=75)
v4=1,8
B5
(b5=40)
v5=2,8
B6
(b6=5)
v6=0,3
0
А1 (а1=50)
U1=0



0
1,0
20


— 0,7
30
2,0
— 0,7
3,0
— 0,7
2,5
0,3
3,5
0
0
А2(а2=20)
U2=-0,6

— 1,6
20
0,4

0,7
3,0


— 0,8
1,0
— 0,8
2,0
— 0,3
3,0
0
-0,7
А3(а3=75)
U3=-1
0
0,7


0,3
20
1,0
0
1,0


0,3
55
0,8
— 0,7
1,5
0
-0,5
А4(а4=80)
U4=-0,3
— 0,3
1,2
0
2,0


0
15
2,0

0
20
1,5
0
40
2,5
5
0
Стоимость 2-ого плана:
D2=1•20+2•30+0,4•20+1•20+0,8•55+2•15+1,5•20+2,5•40=312.
Имеем:u1+v6-c16 =0,3>0, u2+v3-c23 =0,7>0, u3+v3-c33 =0,3>0, u3+v5-c35 =0,3>0. => По аспекту оптимальности, 2-ой план не оптимален. Дальше max(0,3;0,7;0,3;0,3)=0,7 => Поместим перевозку в клеточку А2В3, сместив 15=min(20,30,55,15) по циклу, обозначенному в таблице штрихом. Получим новейшую таблицу. Найдем потенциалы: u1+v1=1,u1+v2=2,u2+v1=0,4,u3+v2=1, u3+v4=0,8, u2+v3=1, u4+v4=1,5, u4+v5=2,5 , u4+v6=0. Положим u1=0,тогда v1=1,u2=-0,6,v2=2,v4=1,8, u3=-1, u4=-0,3,v3=1,6, v5=2,8, v6=0,3. Составим таблицу:
 магазины
магазины
Склад
B1
(b1=40)
v1=1
B2
(b2=50)
v2=2
B3
(b3=15)
v3=1,6
B4
(b4=75)
v4=1,8
B5
(b5=40)
v5=2,8
B6
(b6=5)
v6=0,3
0
А1 (а1=50)
U1=0
0
1,0
35
-1,4
15
2,0
— 0,7
3,0
— 0,7
2,5
0,3
3,5
0
0
А2(а2=20)
U2=-0,6
— 1,6
5
0,4
0
3,0
15
— 0,8
1,0
— 0,8
2,0
— 0,3
3,0
0
-0,7
А3(а3=75)
U3=-1
0
0,7
-0,4
35
1,0
0
1,0



0,3
40
0,8


— 0,7
1,5
0
-0,5
А4(а4=80)
U4=-0,3
— 0,3
1,2
-0,7
2,0
0
2,0


0
35
1,5

0
40
2,5
5
0
Стоимость 3-его плана:
D3=1•35+2•15+0,4•5+1•15+0,8•40+1•35+1,5•35+2,5•40=301,5.
Имеем:u1+v6-c16 =0,3>0,u3+v5-c35 =0,3>0. => По аспекту оптимальности, 3-ий план не оптимален. Дальше max(0,3;0,3)=0,3. => Поместим перевозку в клеточку А3В5, сместив 40=min(40,40) по циклу, обозначенному в таблице штрихом. Получим новейшую таблицу. Чтоб 4-ый план был невырожденным, оставим в клеточке А4В5 нулевую перевозку. Найдем потенциалы: u1+v1=1,u1+v2=2,u2+v1=0,4,u3+v2=1, u4+v5=2,5, u2+v3=1, u4+v4=1,5, u3+v5=1,5 , u4+v6=0. Положим u1=0,тогда v1=1,u2=-0,6,v2=2,v4=1,5, u3=-1,u4=0, v3=1,6, v5=2,5, v6=0. Составим таблицу:
магазины
Склад
B1
(b1=40)
v1=1
B2
(b2=50)
v2=2
B3
(b3=15)
v3=1,6
B4
(b4=75)
v4=1,5
B5
(b5=40)
v5=2,5
B6
(b6=5)
v6=0
А1 (а1=50)
U1=0
1,0
2,0
3,0
2,5
3,5
0
А2(а2=20)
U2=-0,6
0,4
3,0
1,0
2,0
3,0
0
-0,7
А3(а3=75)
U3=-1
0
0,7
-0,4
35
1,0
-0,3
1,0
0
0,8
40
— 1
1,5
0
-0,2
А4(а4=80)
U4=0
0
1,2
-0,4
2,0
0
2,0
0
75
1,5
0
0
2,5
5
0
Стоимость 4-ого плана: D4=1•35+2•15+0,4•5+1•15+1•35+1,5•40+1,5•75=289,5.
Для всех клеток крайней таблицы выполнены условия оптимальности:
1)ui+vj-сij=0 для клеток, занятых перевозками;
2)ui+vj-сij ≤0 для вольных клеток.
Несодержательные ответы:
Прямой ЗЛП:
 35 15 0 0 0 0
35 15 0 0 0 0
5 0 15 0 0 0
X = 0 35 0 0 40 0
0 0 0 75 0 5
min=289,5.
Двоякой ЗЛП:
U1=0 ; U2=-0,6 ; U3=-1 ; U4=0 ; V1=1 ; V2=2 ; V3=1,6 ; V4=1,5 ; V5=2,5 ; V6=0.
max=289,5.
Потому что min=max, то по аспекту оптимальности найдены рациональные решения прямой и двоякой ЗЛП. Содержательный ответ: Нормально перевозить так:
Из А1 в B1 – 35 рулонов полотна;
Из А1 в B2 – 15 рулонов полотна;
Из А2 в B1 – 5 рулонов полотна;
Из А2 в B3 – 15 рулонов полотна;
Из А3 в B2 – 35 рулонов полотна;
Из А3 в B5 – 40 рулонов полотна;
Из А4 в B4 – 75 рулонов полотна.
При всем этом стоимость мала и составит Dmin=289,5. 5 рулонов полотна нужно бросить на складе А4 для их следующей перевозки в остальные магазины.
8.Выводы.
В курсовой работе изложены главные подходы и способы решения транспортной задачки, являющейся одной из более всераспространенных задач линейного программирования. Решение данной задачки дозволяет создать более оптимальные пути и методы транспортирования продуктов, убрать чрезвычайно далекие, встречные, повторные перевозки. Все это уменьшает время продвижения продуктов, уменьшает издержки компаний и компаний, связанные с воплощением действий снабжения сырьем, материалами, топливом, оборудованием и т.д.
метод и способы решения транспортной задачки могут быть применены при решении неких экономических задач, не имеющих ничего общего с транспортировкой груза. В этом случае величины тарифов cij имеют разный смысл зависимо от определенной экономической задачки. К таковым задачкам относятся последующие:
наилучшее закрепление за станками операций по обработке деталей. В их cij является таковым экономическим показателем, как производительность. задачка дозволяет найти, сколько времени и на какой операции необходимо употреблять любой из станков, чтоб обработать наибольшее количество деталей. Потому что транспортная задачка просит нахождения минимума, то значения cij берутся с отрицательным знаком;
рациональные предназначения, либо неувязка выбора. Имеется m устройств, которые могут делать m разных работ с производительностью cij. задачка дозволяет найти, какой механизм и на какую работу нужно назначить, чтоб достигнуть наибольшей производительности;
задачка о сокращении производства с учетом суммарных расходов на изготовка и транспортировку продукции;
повышение производительности авто транспорта за счет минимизации порожнего пробега. Уменьшение порожнего пробега уменьшит количество каров для перевозок, увеличив их производительность;
решение задач при помощи способа воспрещения перевозок. Употребляется в том случае, если груз от некого поставщика по каким-то причинам не быть может выслан одному из потребителей. Данное ограничение можно учитывать, присвоив соответственной клеточке довольно огромное
Таковым образом, значимость решения данной задачки для экономики бесспорна. Приятно обдумывать, что у истоков сотворения теории линейного программирования и решения, в том числе и транспортной задачки, стоял российский ученый – Леонид Витальевич Канторович.
Перечень литературы
1. Кузнецов А.В., Сакович В.А., Холод Н.И. ”Высшая математика. Математическое программирование ”, Минск, Вышейшая школа, 2001г.
2. Красс М.С., Чупрынов Б.П. ”Базы арифметики и ее приложения в экономическом образовании”, Издательство “Дело”, Москва 2001г.
3. В.И. Ермаков “Общий курс высшей арифметики для экономистов”, Москва, Инфра-М, 2000г.
]]>

 (5 оценок, среднее: 4,80 из 5)
(5 оценок, среднее: 4,80 из 5)