Учебная работа. Реферат: Формулы сложения вероятностей

Учебная работа. Реферат: Формулы сложения вероятностей

.

Из пт 2 теоремы, по которой вводилось определение вероятности действия, следует, что если A1
и A2
несовместные действия, то

P(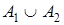) = P(A1
) + P(A2
)

Если A1
и A2
— совместные действия, то 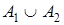=(A1
A2
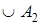), при этом разумеется, что A1
A2
и A2
— несовместные действия. Отсюда следует:

P(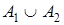) = P(A1
A2
) + P(A2
)

Дальше разумеется: A1
=(A1
A2
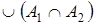), при этом A1
A2
и 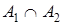– несовместные действия, откуда следует: P(A1
) = P(A1
A2
) + P(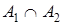) Найдем из данной для нас формулы выражение для P(A1
A2
) и подставим его в правую часть формулы

. В итоге получим формулу сложения вероятностей:

P(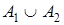)= P(A1
) + P(A2
) – P()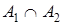

Из крайней формулы просто получить формулу сложения вероятностей для несовместных событий, положив 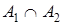= Æ.

Пример 1. Отыскать возможность вынуть туза либо червовую масть при случайном отборе одной карты из колоды в 32 листа.

Р( ТУЗ ) = 4/32 = 1/8; Р( ЧЕРВОВАЯ МАСТЬ ) = 8/32 = 1/4;

Р(ТУЗЧЕРВЕЙ )=1/32;

Р(( ТУЗ ) 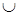(ЧЕРВОВАЯ МАСТЬ )) = 1/8 + 1/4 – 1/32 =11/32

Такого же результата можно было достигнуть при помощи традиционного определения вероятности, пересчитав число подходящих исходов.

Условные вероятности.

Разглядим задачку. Студент перед экзаменом выучил из 30 билетов билеты с номерами с 1 по 5 и с 26 по 30. Понятно, что студент на экзамене вынул билет с номером, не превосходящим 20. Какова возможность, что студент вынул выученный билет?

Определим место простых исходов: W=(1,2,3,…,28,29,30). Пусть событие А состоит в том, что студент вынул выученный билет: А=(1,…,5,25,…,30,), а событие В — в том, что студент вынул билет из первых 20: В=(1,2,3,…,20)

Событие 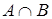состоит из 5 исходов: (1,2,3,4,5), и его возможность равна 5/30. Это число можно представить как произведение дробей 5/20 и 20/30. Число 20/30 – это возможность действия B. Число 5/20 можно разглядывать как возможность действия А при условии, что событие В вышло (обозначим её Р(А/В)). Таковым образом, решение задачки определяется формулой

Р(А/В) = P(АÇВ) /Р(B) (1)

Р(А/В) именуется условной вероятностью действия A при условии, что событие В вышло. Формулу (1) можно разглядывать, как определение условной вероятности. Эту же формулу можно переписать в виде

P(АÇВ)=Р(А/В)Р(B) (2)

Формула (2) именуется формулой умножения вероятностей (аксиомой умножения вероятностей), а условная возможность Р(А/В) тут обязана восприниматься просто по смыслу.

Пример 2. Из урны, содержащей 7 белоснежных и 3 темных шаров, наудачу один за иным извлекают (без возврата) два шара. Какова возможность того, что 1-ый шар будет белоснежным, а 2-ой черным?

Пусть X – событие, состоящее в извлечении первым белоснежного шара, а Y — событие, состоящее в извлечении вторым темного шара. Тогда 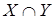– событие, заключающееся в том, что 1-ый шар будет белоснежным, а 2-ой — черным. P(Y/X) =3/9 =1/3 — условная возможность извлечения вторым темного шара, если первым был извлечен белоснежный. Беря во внимание, что P(X) = 7/10, по формуле умножения вероятностей получаем: P(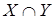) = 7/30

Событие А именуется независящим от действия В (по другому: действия А и В именуются независящими), если Р(А/В)=Р(А). За определение независящих событий можно принять следствие крайней формулы и формулы умножения

P(АÇВ)= Р(А) Р(B)

Обоснуйте без помощи других, что если А и В — независящие действия, то 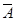и 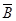тоже являются независящими событиями.

Пример 3. Отыскать возможность того, что при трёх бросках игральной кости трижды выпадет шестёрка. Разумеется, что при любом броске итог не зависит от результатов прошлых бросков, и разыскиваемая возможность равна (1/6)3
=1/216.

Определим в критериях данной для нас задачки возможность того, что при трёх бросках в сумме выпало 4 очка. Выпишем подходящие финалы: “1,1,2”, “1,2,1”, “2,1,1”. Возможность всякого из этих исходов равна 1/216. Потому что все эти финалы несовместимы, интересующая нас возможность будет равна 3/216=1/72.

Пример 4. Из колоды карт в 32 листа извлекается одна карта. Пусть А – событие, состоящее в том, что извлечённая карта – дама. Событие В заключается в том, что извлечённая карта пиковой масти. Разумеется, что Р(А)=4/32=1/8. Вычислим величину возможность того, что извлечённая карта –дама при условии, что эта карта пиковой масти, другими словами Р(А/В). Разумеется, что Р(АÇВ)=1/32, и Р(В)=8/32. Тогда Р(А/В)=Р(АÇВ)/ Р(В)=1/8, другими словами Р(А)=Р(А/В). Отсюда следует, что действия А и В независимы.

Пусть событие С состоит в том, что извлечённая карта не туз. Покажем, что действия А и С зависимы. Разумеется, что Р(АÇС)=Р(А)=1/8. Р(С)=28/32=7/8. Отсюда получаем Р(А/С)=1/7, и это не равно величине Р(А), как следует, действия А и С зависимы.

Пример 5. Разглядим задачку, аналогичную задачке из примера 2, но с одним доп условием: вытащив 1-ый шар, запоминаем его цвет и возвращаем шар в урну, опосля чего же все шары перемешиваем. В данном случае итог второго извлечения никак не зависит от того, какой шар – темный либо белоснежный возник при первом извлечении. Возможность возникновения первым белоснежного шара (событие А) равна 7/10. Возможность действия В – возникновения вторым темного шара – равна 3/10. сейчас формула умножения вероятностей дает: P(АÇВ)=21/100.

Извлечение шаров методом, описанным в этом примере, именуется подборкой с возвращением либо возвратимой подборкой.

Необходимо подчеркнуть, что если в 2-ух крайних примерах положить изначальные количества белоснежных и темных шаров равными соответственно 7000 и 3000, то результаты расчетов тех же вероятностей будут различаться пренебрежимо не много для возвратимой и невозвратной выборок.

Разглядим некие задачки на применение теорем сложения и умножения вероятностей.

1. Три стрелка стреляют в мишень. Любой попадает в мишень либо не попадает в мишень независимо от результатов выстрелов других стрелков. 1-ый стрелок попадает в мишень с вероятностью 0,9, 2-ой – с вероятностью 0,8, а 3-ий – с вероятностью 0,7. Отыскать возможность того, что мишень будет поражена?

вопросец можно поставить по другому: какова возможность того, что хотя бы один стрелок попадёт в мишень? Разумеется, что мишень будет поражена, если все трое попадут в мишень, если в мишень попадут любые двое стрелков, а 3-ий не попадёт и т. д. Пусть событие А заключается в том, что хотя бы один из стрелков попал в мишень. Тогда обратное событие 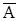состоит в том, что все трое не попали в мишень. Если 1-ый не попадает в мишень с вероятностью 0,1, 2-ой – с вероятностью 0,2, а 3-ий – с вероятностью 0,3, то по аксиоме умножения вероятностей Р(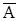)=0,1×0,2×0,3=0,006. Тогда Р(А)=1–Р(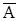)=0,994.

2. При включении движок начинает работать с вероятностью р. а) Отыскать возможность того, что движок начнёт работать с второго включения. б) Отыскать возможность того, что для пуска мотора будет нужно не наиболее 2-ух включений.

а) Для того, чтоб движок начал работать со второго включения, необходимо, во-1-х, чтоб он не запустился при первом включении (событие А). Это происходит с вероятностью 1–р. При втором включении движок запустится (событие В) с вероятностью р. Нас интересует возможность действия АÇВ. Из условия задачки можно осознать, что действия А и В независимы. Отсюда P(АÇВ)=р(1–р).

б) Нас интересует возможность действия, состоящего в том, что движок запустится при первом включении либо при втором включении. Обратное событие состоит в том, что движок не запустится ни при первом, н при втором включении. Возможность этого обратного действия равна (1–р)2
. Отсюда возможность интересующего нас действия равна 1–(1–р)2
.

3. В семье Ивановых 4 ребёнка. Понятно, что один из деток – мальчишка. Отыскать возможность того, что все малыши –мальчишки. Принять возможность рождения мальчугана и возможность рождения девченки равными 1/2 и не зависящими от того, какого пола малыши уже имеются в семье.

Пусть событие В заключается в том, что все малыши в семье – мальчишки, событие А заключается в том, что в семье есть хотя бы один мальчишка (конкретно так мы должны осознавать условие задачки). Нас интересует величина Р(В/А). Для того, чтоб пользоваться формулой условной вероятности, нужно, во-1-х, вычислить P(АÇВ). В нашем случае событие А является следствием действия В, потому P(АÇВ)=Р(В) (смотри разъяснение к теме 2). По условию задачки Р(В)=(1/2)4
=1/16. Чтоб вычислить Р(А), заметим, что событие 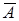заключается в том, что все малыши в семье –девченки. Разумеется, что Р(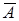)=(1/2)4
=1/16. Тогда Р(А)=1–Р(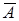)=15/16. сейчас можно пользоваться формулой для определения условной вероятности Р(В/А) = P(АÇВ)/Р(А). В итоге выходит Р(В/А)=(1/16)/( 15/16)=1/15.

Если б в условии данной для нас задачки был поставлен вопросец “чему равна возможность того, что все малыши мальчишки, при условии, что 2-ой ребёнок – мальчишка?”, то ответ был бы 1/8.

4. В урне 7 белоснежных и три чёрных шара. Без возврата извлекаются 3 шара. Понятно, что посреди их есть чёрный шар. Отыскать возможность того, что остальные два шара белоснежные.

Пусть событие А заключается в том, что в выборке есть два белоснежных шара, событие В – в том, что в выборке есть чёрный шар. Всего в условии задачки существует 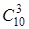вероятных исходов. Отсюда Р(АÇВ)=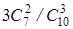. Чтоб вычислить возможность Р(В), заметим, что 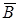заключается в том, что все извлечённые шары белоснежные, и Р(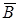)=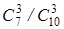. Разыскиваемая возможность равна (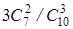)/(1–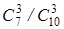)=63/85.

5. Отыскать возможность того, что при бросании трёх игральных костей хотя бы на одной выпадет 6 очков при условии, что на всех костях выпали грани с чётным числом очков.

Пусть событие А заключается в том, что хотя бы на одной кости выпало 6 очков, а событие В–в том, что на всех костях выпало чётное число очков. Вычислим возможность действия АÇВ. Общее число исходов, разумеется равно 63
=216. Одним из подходящих исходов является выпадение 6-ти очков на всех трёх костях. Имеется 6 исходов, состоящих в выпадении шестёрок на 2-ух костях и выпадении чётного числа очков, но не шестёрки на третьей кости. Можно высчитать 12 исходов, когда на одной кости выпадает шестёрка, а на 2-ух остальных–чётные числа очков, но не шестёрки. Таковым образом, событию АÇВ способствуют 19 исходов, откуда Р(АÇВ)=19/216. Разумеется, что Р(В)=(1/2)3
=1/8. Разыскиваемая возможность равна (19/216)/(1/8)=19/27.

6. Студент понимает 20 из 25 вопросцев программки. Зачёт сдан, если студент ответит не наименее чем на 3 из 4-х вопросцев в билете. Взглянув на 1-ый вопросец, студент нашел, что понимает его. Какова возможность, что студент сдаст зачёт?

Пусть А – событие, заключающееся в том, что студент сдал экзамен;

В – событие, заключающееся в том, что студент понимает 1-ый вопросец в билете.

Разумеется, что Р(В) =20/25=4/5. сейчас нужно найти возможность Р(АÇВ). Из 25-ти вопросцев всего можно составить 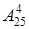разных билетов, содержащих 4 вопросца. Все билеты, выбор которых удовлетворял бы и событию А и событию В, должны быть составлены последующим образом: или студент понимает все вопросцы билета (можно составить всего 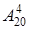таковых билетов), или студент понимает 1-ый, 2-ой и 3-ий вопросцы, но не понимает четвёртого (можно составить всего 5 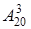таковых билетов), или студент понимает 1-ый, 2-ой и четвёртый вопросцы, но не понимает третьего (тоже 5 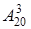билетов), или студент понимает 1-ый, 3-ий и четвёртый вопросцы, но не понимает второго (тоже 5 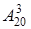билетов). Отсюда получаем, что

Р(АÇВ) =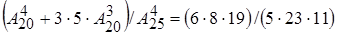

Осталось лишь отыскать разыскиваемую возможность р(А/В):

Р(А/В) =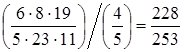

задачки для самостоятельного решения.

1) Обосновать формулу

Р(АÈВÈС)=Р(А)+ Р(В)+Р(С)–Р(АÇВ)–Р(АÇС)–Р(ВÇС)+Р(АÇВÇС)

2) Возможность попасть в самолёт равна 0,4, возможность его сбить равна 0,1. Отыскать возможность того, что при попадании в самолёт он будет сбит.

3) Из урны, содержащей 6 белоснежных и 4 чёрных шара, наудачу извлекают по одному шару до возникновения чёрного шара. Отыскать возможность того, что придётся создавать четвёртое извлечение, если подборка делается а)с возвращением; б) без возврата.

4) а) В критериях задачки 1 отыскать возможность того, что в мишень попали двое стрелков. б) В критериях задачки 1 отыскать возможность того, что в мишень попали не наименее 2-ух стрелков.

5) По самолёту делается три выстрела. Возможность попадания при первом выстреле равна 0,5, при втором – 0,6, при 3-ем–0,8. При одном попадании самолёт будет сбит с вероятностью 0,3, при 2-ух–с вероятностью 0,6, при трёх самолёт будет сбит наверное. Какова возможность того, что самолёт будет сбит?

6) В критериях задачки 4 отыскать возможность того, что на всех костях выпала шестёрка, если понятно, что а) по последней мере, на 2-ух костях выпало однообразное число очков; б) на всех костях выпало однообразное число очков.

7) Бросаются три игральных кости. Какова возможность того, что на одной из их выпадет единица, если на всех трёх костях выпали различные грани?

8) Возможность того, что случайным образом избранный из студенческой группы студент понимает британский язык, равна 5/6. Возможность того, что студент понимает французский язык, равна 7/12. Возможность того, что студент понимает и британский и французский языки, равна 1/2. а) Отыскать возможность того, что студент не понимает французского языка при условии, что он не понимает британского. б) Отыскать возможность того, что студент понимает французский язык при условии, что он понимает британский.

9) Понятно, что при бросании 10 игральных костей выпала хотя бы одна единица. Какова возможность того, что выпало две либо наиболее единиц?

10) Цех изготовляет кинескопы для телевизоров, при этом 70% всех кинескопов предусмотрены для цветных телевизоров и 30% – для мониторов. Понятно, что 50% всей продукции отчаливает на экспорт, при этом из общего числа кинескопов, созданных для цветных телевизоров, 40% отчаливает на экспорт. Отыскать возможность того, что наудачу взятый для контроля кинескоп предназначен для монитора, если понятно, что он будет выслан на экспорт.

11) В ящике лежат 12 бардовых, 8 зелёных и 10 голубых шаров. Наудачу вынимают два шара. Отыскать возможность того, что будут вынуты шары различного цвета при условии, что не вытащат голубий шар.

Ответы. 2)1/4; 3) а) 0,216; б) 1/6; 4) а) 0,398; б) 0,902; 5) 0,594; 6) а) 1/96; б) 1/6; 7) 0,5; 8) а) 0,5; б) 0,3; 9)1-10×59
/(610
–510
); 10) 0,44; 11) 48/95.

]]>