Учебная работа. Реферат: Матричные операции в вейвлетном базисе

Учебная работа. Реферат: Матричные операции в вейвлетном базисе

Курсовая работа студентки 3 курса Громовой Марии Михайловны

Белорусский муниципальный институт

Факультет прикладной арифметики и информатики

Кафедра математической физики

Минск 2003

Введение

Вейвлет-преобразование сигналов (wavelet transform), теория которого оформилась сначала 90-х годов, является не наименее общим по областям собственных применений, чем традиционное преобразование Фурье. Принцип ортогонального разложения по малогабаритным волнам состоит в способности независящего анализа функции на различных масштабах ее конфигурации. Вейвлет-физиологии (Физиология от греч. — природа и греч. — знание — наука о сущности живого) зрительной системы, в анализе радарных сигналов и пророчестве землетрясений. К огорчению, размер русской научной литературы по теме вейвлет-преобразований (ну и нейронных сетей) относительно невелик.

Базисная мысль всходит к временам 200-летней давности и принадлежит Фурье: аппроксимировать сложную функцию взвешенной суммой обычных функций, любая из которых, в свою очередь, выходит из одной функции-прототипа. Эта функция-прототип делает роль строительного блока, а разыскиваемая аппроксимация выходит комбинированием схожих по структуре блоков. При всем этом, если «отменная» аппроксимация выходит при использовании маленького числа блоков, то тем достигается существенное уплотнение инфы. В качестве таковых блоков Фурье употреблял синусоиды с разными периодами.

Что до этого всего различает вейвлет-анализ от анализа Фурье? Главным недочетом Фурье-преобразования является его «глобальная» чувствительность к «локальным» скачкам и пикам функции. При всем этом модификация коэффициентов Фурье (к примеру, обрезание больших гармоник с целью фильтрации шума) заносит схожие конфигурации в определения. Это изюминка оказывается полезной для стационарных сигналов, характеристики которых в целом не много изменяются со временем.

При исследовании же нестационарных сигналов требуется внедрение неких локализованных во времени малогабаритных волн, коэффициенты разложения по которым сохраняют информацию о дрейфе характеристик аппроксимируемой функции. 1-ые пробы построения таковых систем функций сводились к сегментированию сигнала на фрагменты («окна«) с применением разложения Фурье для этих фрагментов. Соответственное преобразование — оконное преобразование Фурье — было предложено в 1946-47 годах Jean Ville и, независимо, Dennis Gabor. В 1950-70-х годах различными создателями было размещено много модификаций времени-частотных представлений сигналов.

В конце 70-х инженер-геофизик Морли (Jean Morlet) столкнулся с неувязкой анализа сигналов, которые характеризовались частотной компонентой в течение недлинного промежутка времени и низкочастотными колебаниями при рассмотрении огромных временных масштабов. Оконные преобразования дозволяли проанализировать или высочайшие частоты в маленьком окне времени, или низкочастотную компоненту, но не оба колебания сразу. В итоге был предложен подход, в каком для разных диапазонов частот использовались временные окна различной продолжительности. Оконные функции выходили в итоге растяжения-сжатия и смещения по времени гаусиана. Morlet именовал эти базовые функции вейвлетами (wavelets) — малогабаритными волнами. В предстоящем благодаря работам Мейера (Yves Meyer), Добеши (Ingrid Daubechies), Койфмана (Ronald Coifman), Маллы (Stephane Mallat) и остальных теория вейвлетов заполучила свое современное состояние.

Посреди русских ученых, работавших в области теории вейвлетов, нужно отметить С.Б. Стечкина, И.Я. Новикова, В.И. Бердышева.

1. Многомасштабный анализ и вейвлеты

Определение 1. Многомасштабный анализ (multiresolutional analysis) – разложение гильбертова места L2
(Rd
), d³1, в последовательность замкнутых подпространств

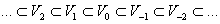, (1.1)

владеющих последующими качествами:

1. 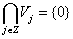, и 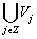много в L2
(Rd
),

2. Для хоть какого fÎ L2
(Rd
), для хоть какого jÎ Z, f(x)ÎVj
и тогда лишь тогда, когда

f(2x) ÎVj-1
,

3. Для хоть какого fÎ L2
(Rd
), для хоть какого kÎ Zd
, f(x)ÎV0
и тогда лишь тогда, когда f(x-k)ÎV0
,

4. Существует масштабирующая (scaling) функция jÎV0
, что {j(x-k)}kÎZ
d
образует

базис Ритца в V0
.

Для ортонормальных базисов можно переписать свойство 4 в виде:

4’. Существует масштабирующая функция jÎV0
, что {j(x-k)}kÎZ
d
образует ортонормальный базис в V0
.

Определим подпространство Wj
как ортогональное дополнение к Vj
в Vj-1
,

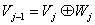, (1.2)

и представим место L2
(Rd
) в виде прямой суммы

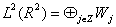(1.3)

Выбирая масштаб n, можем поменять последовательность (1.1) последующей последовательностью:

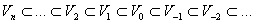(1.4)

и получить

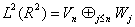(1.5)

Если имеем конечное число масштабов, то, не нарушая общности, можно положить j=0 и разглядывать

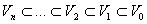, V0
Î L2
(Rd
) (1.6)

заместо (1.4). В числовой реализации подпространство V0
конечномерно.

Функция j — так именуемая масштабирующая (скейлинг-) функция. С ее помощью можно найти функцию y — вейвлет — такую, что набор {y(x-k)}kÎZ
образует ортонормальный базис в W0
. Тогда

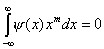, m=0..M-1. (1.7)

Из характеристики 4’ конкретно следует, что, во-1-х, функция j быть может представлена в виде линейной композиции базовых функций места V-1
. Потому что функции {jj,k
(x)=2-j/2
j(2-j
x-k)}kÎZ
образуют ортонормальный базис в Vj
, то имеем

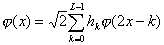. (1.8)

Совершенно говоря, сумма в выражении (1.8) не должна быть конечной. Можно переписать (1.8) в виде

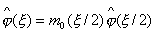, (1.9)

где

, (1.10)

а 2p-периодическая функция m0
определяется последующим образом:

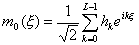. (1.11)

Во-2-х, ортогональность {j(x-k)}kÎZ
предполагает, что

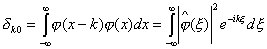(1.12)

и означает

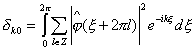(1.13)

и 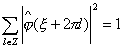. (1.14)

Используя (1.9), получаем

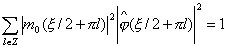(1.15)

и, рассматривая сумму в (1.15) по четным и нечетным индексам, имеем

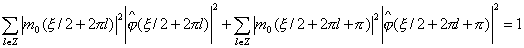. (1.16)

Используя 2p-периодичность функции m0
и (1.14), опосля подмены x/2 на x, получаем нужное условие

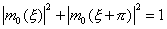(1.17)

для коэффициентов hk
в (1.11). Заметив, что

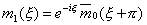(1.18)

и определив функцию y последующим образом:

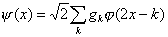, (1.19)

где

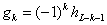, k=0,…,L-1 , (1.20)

либо преобразование Фурье для y

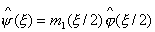, (1.21)

где

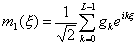, (1.22)

можно показать, что при любом фиксированном масштабе jÎZ вейвлеты

{yj,k
(x)=2-j/2
y(2-j
x-k)}kÎZ
образуют ортонормальный базис места Wj
.

Равенство (1.17) описывает пару квадратурных зеркальных фильтров (quadrature mirror filters, QMF) H и G, где 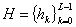и 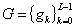. Коэффициенты QMF H и G рассчитываются при помощи решения системы алгебраических уравнений. Число L коэффициентов фильтра в (1.11) и (1.22) соединено с числом исчезающих моментов М, и постоянно четно.

Избранный фильтр Н вполне описывает функции j и y и, таковым образом, многомасштабный анализ. Не считая того, в верно построенных методах значения функций j и y практически никогда не рассчитываются. Благодаря рекурсивному определению вейвлетного базиса, все операции проводятся с квадратурными зеркальными фильтрами H и G, даже если в их употребляются величины, связаные с j и y.

2. Резвое вейвлет-преобразование

Опосля того, как вычислены коэффициенты hk
и gk
, т.е. избран определенный вейвлет, можно проводить вейвлет-преобразование сигнала f(x), так как задан ортонормальный базис (yj,k,
j j,k
). Неважно какая функция f(x)ÎL2
(R) вполне характеризуется ее вейвлет-коэффициентами разложения по этому базису и поэтому быть может представлена формулой

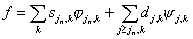. (2.1)

Зададим все пределы суммирования в формуле (2.1). Функцию f(x) можно разглядывать на любом n-м уровне разрешения jn
. Тогда разделение меж ее усредненными значениями на этом уровне и флуктуациями вокруг их смотрятся как

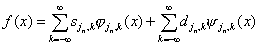. (2.4)

На нескончаемом интервале 1-ая сумма быть может опущена, и в итоге выходит «незапятнанное» вейвлет-разложение.

Коэффициенты sj,k
и dj,k
содердат информацию о составе сигнала на различных масштабах и рассчитываются по формулам:

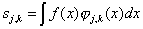, (2.2)

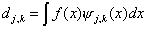. (2.3)

Но при всем этом компьютерные расчеты занимают достаточно долгое время, т.к. при вычислении приходится проводить O(N2
) операций, где N – число имеющихся значений функции. Опишем наиболее резвый метод.

В настоящих ситуациях с оцифрованным сигналом мы постоянно имеем дело с конечным набором цифр (точек). Потому постоянно существует лучший уровень разрешения, когда любой интервал содержит по одному числу. Соответственно и суммирование по k будет идти в конечных границах. Комфортно поменять шкалу разрешения (либо шкалу f), приписав случае просто вычислить вейвлет-коэффициенты для наиболее усредненных уровней j³1. Многомасштабный анализ приводит естественным методом к иерархической и резвой схеме вычисления вейвлет-коэффициентов данной функции.

В общем случае итерационные формулы резвого вейвлет-преобразования имеют вид:

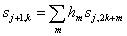, (2.4)

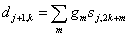(2.5)

с

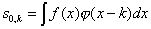. (2.6)

Эти уравнения обеспечивают резвые (либо пирамидальные) методы вычисления вейвлет-коэффициентов, так как требуют лишь O(N) операций для собственного окончания. Начав с s0,k
, мы вычислим все остальные вейвлет-коэффициенты, если характеристики вейвлета hm
и gm
известны. Очевидный вид вейвлета при всем этом не употребляется. Обычная форма приобретенных итерационных уравнений служит единственным оправданием введения множителя 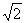в функциональное уравнение (1.8). В принципе, коэффициенты hm
и gm
можно было бы перенормировать. Но, уравнения (2.4), (2.5) употребляются на практике существенно почаще остальных, и потому эту нормировку не изменяют. Любые доп сомножители в их могут привести только к усложнению численных расчетов.

Остающиеся задачи соединены с исходными данными. Если известен очевидный вид функции f(x), то коэффициенты s0,k
можно вычислить, используя формулу (2.6). Но ситуация различается от данной, если доступны лишь дискретные значения f(x). Чтоб достигнуть высочайшей точности, отлично бы задать весьма малые интервалы (плотную сетку), но это часто труднодоступно из-за конечности интервалов сбора инфы. В таком случае простейшее принимаемое решение состоит в конкретном использовании величин f(k) из доступного набора данных в виде коэффициентов s0,k
и применении резвого вейвлет-преобразования с внедрением формул (2.4), (2.5). Это неопасная операция, т.к. пирамидальный метод обеспечивает полную реконструкцию сигнала, а коэффициенты s0,k
на самом деле представляют собой локальные средние значения сигнала, взвешенные со скейлинг-функцией.

В общем случае можно избрать

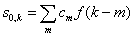. (2.7)

Рассмотренная ситуация отвечает условию s0,k
=f(k), что соответствует cm
=d0m
.

Оборотное резвое вейвлет-преобразование дозволяет реконструировать функцию по значениям ее вейвлет-коэффициентов.

3. Двумерные вейвлеты

Многомасштабный анализ можно проводить и с многомерными функциями. Существует два метода обобщить его на двумерный вариант, но почаще употребляется построение, данное тензорными произведениями.

Очевидный путь построения двумерного ортонормального базиса исходя из одномерного ортонормального вейвлет-базиса yj,k
(x)=2j/2
y(2j
x-k) заключается в том, чтоб методом тензорного произведения образовать надлежащие функции из 2-ух одномерных базисов:

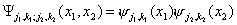. (3.1)

В этом базисе две переменных x1
и x2
сжимаются по-разному.

Больший Энтузиазм для почти всех приложений имеет иная система, в какой масштабирование приобретенного ортонормального вейлет-базиса происходит по обеим переменным схожим образом и двумерные вейвлеты задаются последующим выражением:

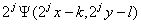, j,k,lÎZ, (3.2)

но Y уже не является единственной функцией, напротив, она будет сформирована из 3-х простых вейвлетов. Чтоб сделать ортонормальный базис W0
, сейчас придется употреблять три семейства

, , .

Тогда двумерные вейвлеты запишутся в виде

, , .

На двумерной плоскости происходит анализ по горизонталям, вертикалям и диагоналям с схожим разрешением в согласовании с 3-мя выписанными выше вейвлетами.

4. Матричные операции

4.1 Матричное умножение

Существует два вероятных метода повлиять оператором на функцию в рамках вейвлет-теории. Они именуются обычным и необычным матричным умножением.

У довольно гладких функций большая часть их вейвлет-коэффициентов довольно мелкие. Для широкого класса операторов большая часть их матричных частей также оказываются маленькими. Разглядим структуру тех частей матричного представления некого оператора Т, которые довольно значительны. Матричные элементы удовлетворяют последующим соотношениям.

при , (4.1.1)

при , (4.1.2)

Топология распределения этих матричных частей снутри матрицы может оказаться очень запутанной.

Рассметрим действие оператора Т на функцию f, которое превращает ее в функцию g.

(4.1.3)

Как g, так и f могут быть представлены в виде вейвлет-рядов с вейвлет-коэффициентами (f
sj,k
;f
dj,k
) и (g
sj,k
;g
dj,k
). На более детализированном уровне разрешения jn
отличны от нуля лишь s-коэффициенты, и преобразование имеет вид

. (4.1.4)

На последующем уровне получаем

, (4.1.5)

, (4.1.6)

где

и подмена нижних индексов S®D соответствует подстановке j®y под знаком интеграла.

Имеется связь меж различными уровнями, поэтому что все s-коэффициенты на этом (jn
-1)-м уровне должны быть разложены при помощи резвого вейвлет-преобразования на s- и d-коэффициенты наиболее больших уровней. Потому, даже имея практически диагональный вид на исходном шаге, обычная матрица преобретает потом достаточно непростой вид, как это показано на рис.1.

На конечном шаге мы имеем дело с вейвлет-представлением, описываемым формулой (2.1), в какой в векторах остается лишь один s-коэффициент, представляющий взвешенное среднее функции по всему интервалу ее задания, а SS-переход от f к g описывается верхним левым квадратиком на этом рисунке. В то же время на пути к данной формуле от скейлинг-представления нам приходилось иметь дело со средними величинами на промежных уровнях, разлагая их потом на любом шаге на части, s и d, следующих уровней разрешения. Эти промежные s-коэффициенты были опущены, поэтому что мы подменяли их на s- и d-коэффициенты поледующих уровней. Конкретно потому окончательная матрица при обычном подходе приобретает таковой непростой вид.

Рис.1. Матричное части матрицы с ненулевыми вейвлет-коэффициентами заштрихованы.

С целью упрощения вида матричного представления было предложено употреблять переопределенный набор вейвлет-коэффициентов. Сохраним эти усредненные величины в виде соответственных промежных s-коэффициентов как в исходных, так и в конечных векторах, представляющих функции f и g. естественно, в этом случае придется иметь дело с приводимыми векторами, которые намного больше требуемых для конечного ответа. Но, известен метод приведения этих переопределенных выражений к конечной непереопределенной форме. В то же время таковым образом можно значительно упростить вид матрицы преобразования и численные расчеты.

Рис.2. Необычное матричное умножение при вейвлет-анализе.

Разные уровни оказались вполне развязанными, поэтому что в матрице сейчас вполне отсутствуют блоки, которые ранее перепутывали их. Блок с SS-элементами извлечен, а на его пространство вставлена нулевая матрица. Полная матрица соответстваенно искусственным образом возросла. совместно с ней возросли и векторы, характеризующие функции f и g. сейчас тут удерживаются все промежные s-коэффициенты вейвлет-разложения функции f. Любой блок Sj+1
выходит из Sj
и Dj
. В матрице преобразования равны нулю все SS-элементы кроме их величин на низшем уровне S0
S0
. Все другие SD-, DS-, DD-матрицы практически диагональны вследствие конечности области задания вейвлетов и скейлинг функций. Приведенная на рис. 2 форма функции g преобразуется в ее обыденное вейвлет-стремительно.

4.2 Воззвание матрицы

Утверждение 1. Последовательность матриц Xk
такая, что

Xk+1
=2Xk
-Xk
АXk
, (4.2.1)

X0
=aА*
, (4.2.2)

где А*
— сопряженная матрица и a выбирается таковым образом, чтоб наибольшее собственное

Если это утверждение скомбинировать с методом резвого матричного умножения, то выходит метод для построения оборотной матрицы в обычной форме с трудозатратностью и в необычной форме с трудозатратностью , где R – число обусловленности матрицы. При помощи числа R можно оценить соотношение меж большим и минимальным сингулярными числами выше порога точности.

4.3 Вычисление экспоненты, синуса и косинуса от матрицы.

При воззвания матрицы употреблялся ранее узнаваемый метод, который выходит на совсем другой уровень, когда применяется совместно с вейвлет-представлением.

метод вычисления экспоненты матрицы основывается на тождестве

. (4.3.1)

Во-1-х, exp(2-L
A) быть может посчитана, к примеру, при помощи ряда Тейлора. Число L выбирается таковым образом, чтоб наибольшее сингулярное число матрицы 2-L
A было меньше единицы. На втором шаге метода для заслуги результата матрица 2-L
A возводится в квадрат L раз.

Аналогично, синус и косинус от матрицы могут быть посчитаны с исподьзованием формул двойного угла.

(4.3.2)

, (4.3.3)

при l=0,…,L-1

(4.3.4)

, (4.3.5)

где I – тождество. опять избираем L таковым образом, чтоб наибольшее сингулярное число матрицы 2-L
A было меньше единицы, вычисляем синус и косинус матрицы 2-L
A, при помощи рядов Тейлора, а потом используем формулы (4.3.4) и (4.3.5).

Обычно такие методы требуют по наименьшей мере O(N3
) операций, потому что должне быть выполнено довольно много операций по умножению густых матриц. Резвый метод для умножения матриц в обычной форме уменьшает сложность до не наиболее чем операций, а резвый метод для умножения матриц в необычной форме – до O(N) операций.

Перечень
литературы

Beylkin G. Wavelets and Fast Numerical Algorithms.

Beylkin G. Wavelets, Multiresolution Analysis and Fast Numerical Algorithms.

Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их внедрение // Успехи физических наук – 2001, №5. – С.465-500

]]>