Учебная работа. Реферат: Мир глазами Нильса Бора: волны и их восприятие

Учебная работа. Реферат: Мир глазами Нильса Бора: волны и их восприятие

Волны и частички в традиционном естествознании.

Вещество в традиционной теории обычно рассматривается как совокупа дискретных неразделимых частиц — вещественных точек. Зависимо от рассматриваемой задачки в их роли могут выступать макроскопические объекты, молекулы, атомы и т.д.

Введение в естествознание концепции поля, почти всегда описываемого непрерывными и обращающимися на бесконечности в 0 очень сложными функциями координат и времени 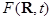, ставит вопросец о их разложении по наиболее обычным “базовым” функциям, с которыми легче создавать расчеты. Такое случае “обыденных“ векторов число ортогональных координатных осей и соответственных им базовых векторов (размерность места) очень ограничено (в евклидовом пространстве их 3), место же непрерывных функций оказывается нескончаемо мерным, число частей его базиса нередко оказывается даже несчетным. В качестве базовых могут выбираться разные наборы функций. В большинстве задач более комфортны гармонические: синусы и косинусы. Аксиома о разложении в ряды и интегралы Фурье утверждает, что неважно какая довольно гладкая функция быть может представлена как суперпозиция (сумма либо интеграл) гармонических функций с разными частотами.

В случае зависящей лишь от времени начальной функции 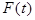о ее Фурье разложении молвят как о представлении в виде суммы гармонических колебаний разных частот 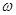, каждое из которых имеет вид

(1) .

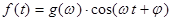В природе встречается огромное количество действий, представляющих из себя практически гармонические колебания (напр. изменение электронного поля в конденсаторе, включенном в цепь осциллирующего контура , обширно применяемого в качестве маятника в электрических часах). По существу все системы, имеющие точки устойчивого равновесия, могут совершать гармонические колебания поблизости этих точек.

Если рассматриваемая функция зависит лишь от пространственных координат 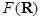, она быть может представлена суммой пространственных гармоник вида:

(2) .

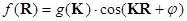В общем случае функций, зависящих и от координат и от времени, их можно представить в виде суммы плоских монохроматических волн, любая из которых описывается математическим выражением вида:

(3) .

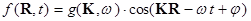Кроме плоских волн время от времени употребляют разложения на сферические, цилиндрические и др. монохроматические волны. В качестве примера приведена “моментальная фото” радиальных (двухмерных сферических) волн. Примерами объектов природы, приближенно описываемых отдельными плоскими монохроматическими волнами, являются волны на поверхности моря (без “гребешков”), звуковые волны от камертона, излучение лазера.

Т.о. монохроматические волны, как и точечные частички, являются не столько понятиями, отражающими характеристики реально имеющихся объектов, сколько моделями, значительно облегчающими математическое рассмотрение явлений природы. наличие ряда объектов и явлений, приближенно описываемых этими моделями, привело к их некой абсолютизации на традиционном шаге развития естествознания.

Математический формализм описания волн и частиц.

Функцию, описывающую плоскую монохроматическую волну (3), комфортно записывать с внедрением многомерных обозначений в всеохватывающем виде

(4) ,

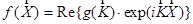при этом символ операции взятия вещественной части всеохватывающего числа обычно ради сокращенности опускается.

Для описания распределения плотностей (массы, заряда, спина и т.д.) точечных объектов вводят так именуемые дельта-функции , математические характеристики которых очень экзотичны:

(5) ,

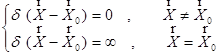при этом на бесконечность функция уходит так “далековато”, что размер под ее графиком оказывается равным конечной величине — 1.

,

Хоть какой вектор R быть может разложен по избранному базису:

(7) ,

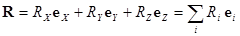т.е. представлен как сумма единичных ортов, домноженных на числа, именуемые проекциями вектора на направление орта . Выражение для проекций выходит с учетом (6) в итоге скалярного умножения (7) на любой из ортов:

(8) .

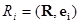В многофункциональном пространстве роль векторов играют непрерывные функции, роль скалярного произведения (операция, ставящая в соответствие двум векторам число) — интеграл по конфигуранционному месту аргументов от их произведения:

(9) .

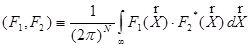Роль ортонормированного базиса может играться огромное количество гармонических функций:

(10) ,

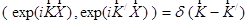при этом дельта функция в (10) является аналогом знака Кронекера в (6). Аксиома о разложении в интеграл Фурье, имеющая вид:

(11)

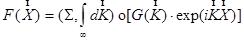
подобна разложению (7), при этом амплитуды волн (“проекции функции F на гармонические отры”) находятся аналогично тому, как это делалось для векторов в (8):

(12) .

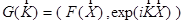Кроме гармонических функций существует нескончаемое огромное количество остальных ортонормированных наборов, определенный выбор которых определяется специфичностью задачки. А именно, могут употребляться и дельта-функции, серьезное математическое определение которых аналогично разложениям (7) и (11):

(13) .

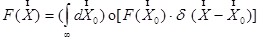Т.о. исходя из убеждений арифметики дельта функции (описывающие точечные частички) и гармонические функции (описывающие монохроматические волны) составляют ортонормированные наборы и могут употребляться для разложения наиболее сложных функций и идиентично подходящи для описания объектов и действий с очень различными качествами.

Акустические волны. Звук представляет собой продольные волны сжатия, распространяющиеся в упругих вещественных средах. В жестких телах вероятен “поперечный” звук. Ухо человека принимает колебания, частоты которых лежат в спектре от ?? Гц до Гц ??. Высота звука определяется частотой колебаний: наиболее высочайшие частоты вызывают чувство “наиболее высочайшего звука”, “басы” соответствуют низкочастотным колебаниям. чувство громкость звука определяется энергией, переносимой звуковой волной (пропорциональна квадрату амплитуды колебаний давления).

Органы слуха млекопитающих представляют собой очень совершенный акустический устройство, позволяющий регистрировать звук в широких спектрах громкости (“сила возникающего чувства” пропорциональна логарифму энергии). Базу “входного устройства” звукового канала составляет акустический резонатор, выделяющий и усиливающий из различных акустических колебаний только те, что лежат в спектре восприятия. Главная роль в анализе звука принадлежит особым упругим волоскам разных размеров, связанных с чувствительными нервными окончаниями. Гармонические Фурье-составляющие, на которые можно разложить звуковые колебания, вследствие явления резонанса (резкое повышение амплитуды колебаний при совпадении своей и вынуждающих частот) очень раскачивают волоски строго определенных размеров, что вызывает возникновения импульсов в соответственных системы животных, обычно расположенный в головном отделе тела и представляющий собой компактное скопление нервных клеток и их отростков), где и возникает чувство звука (эта часть процесса восприятия исследована более плохо). Т.о, в ухе происходит фурье-анализ звуковых колебаний.

Колебания воздуха, создаваемые свободно колеблющимися струнами, очень близки к гармоническим (”незапятнанный звук”), хотя и содержат малые примеси частот, кратных главной — обертоны. Их наличие разъясняет факт различного звучания одной и той же нотки на различных инструментах. Обертоны “несут ответственность” за определение речи: при произношении гласных звуков голосовые связки человека делают надлежащие его высоте голоса частоты, очень богатые обертонами. движение языка и губ изменяют форму ротовой полости, выполняющей роль акустического резонатора, и, как следствие, — режимы затухания разных гармоник.

Музыкальные звуки представляют собой смесь нескольких гармонических колебаний, частоты которых относятся как маленькие целые числа и вызывают у человека приятные чувства (механизм крайнего не выяснен). Близкие, но отличающиеся по частоте колебания вызывают противные чувства диссонирующего звука. Звуковые колебания со сплошными диапазоном частот воспринимаются человеком как шум.

Колебания плотности с частотами, лежащими ниже частотного порога восприятия, именуются инфразвуком. Имеются данные о том, что интенсивный инфразвук определенных частот может оказывать очень неблагоприятное воздействие на человека, что по-видимому соединено с его резонансным действием на протекающие в организме повторяющиеся процессы.

Акустические колебания с частотами, превосходящими порог восприятия, носят наименования ультразвука. Ультразвук обширно употребляется в локации в вариантах, когда расстояния до объекта настолько малы, что измерение времени распространения электромагнитных волн преобразуется в трудозатратную задачку. Возникающий при отражении звуковых волн от передвигающихся объектов эффект Доплера дозволяет определять скорости наблюдаемого объекта

Видимый свет представляет собой поперечные электромагнитные волны, лежащие в частотном спектре от ?? Гц до ??Гц . Вызываемое им чувство яркости определяется логарифмом энергии световой волны (энергия пропорциональна квадрату амплитуды). глаза человека и ряда высших млекопитающих способны производить частотный Фурье-анализ электромагнитного поля, создавая разные чувства цвета. Изменение цветов при движении по диапазону от красноватого до фиолетового соответствует повышению частот монохроматических гармоник электромагнитного поля.

Ниже пределов чувствительности людского глаза на шкале частот электромагнитного излучения лежит инфракрасное излучение , безпрерывно переходящее в радиоволны. Их био действие в подавляющем большинстве случаев сводится к эффектам, связанным с нагреванием. Ультрафиолетовое, рентгеновское и палитра излучения характеризуются частотами, лежащими выше предела зрительного восприятия.

Возрастание частоты электромагнитного излучения сопровождается повышением его вредного действия на био объекты.

Индивидуальности цветного зрения. Увлекательной физиологической индивидуальностью зрения является тот факт, что определенным образом подобранная смесь монохроматических излучений может создавать буквально такое же чувство: как другое монохроматическое излучение (смесь красноватого и желтоватого цветов воспринимается как оранжевый, а не “красно-желтый”). Разъяснение кроется в строении светочувствительных клеток — палочек и колбочек, образующих сетчатку глаза. Наиболее чувствительные палочки реагируют лишь на энергию световой волны (в сумерках изображения теряют собственный цвет), а колбочки содержат три сорта зрительного пигмента, имеющие разные кривые спектральной чувствительности . В итоге протекающих в их физико-химических действий при облучении клеток формируются электронные импульсы, величины которых определяются произведением интенсивности световой гармоники на чувствительность пигмента на ее частоте. Т.о. преобразование световых сигналов при зрительном восприятии с математической точки зрения может рассматриваться как проектирование из бесконечномерного места амплитуд Фурье-гармоник электромагнитного поля в трехмерное место электронных импульсов. Всякое проектировании на подпространство наименьшей размерности сопровождается частичной потерей инфы, что и приводит к неоднозначности цветового восприятия.

Физиологические индивидуальности зрительного восприятия образов. Физико-химические процессы преобразования оптических сигналов в химические являются первым звеном в длинноватой цепи, приводящей к формированию в сознании зрительного вида. Почти все звенья данной цепи исследованы очень неполно.

Светочувствительные клеточки сетчатки соединены не только лишь с системы животных, обычно расположенный в головном отделе тела и представляющий собой компактное скопление нервных клеток и их отростков) определяется как физическая и био сеть, производящую первичную обработку зрительных сигналов и являющуюся вынесенной вперед частью мозга . О трудности действий формирования зрительного вида молвят последующие индивидуальности нашего восприятия:

1. Оптическая система глаза сформировывает на сетчатке перевернутое изображение, что не отражается на восприятии. При использовании особых оптических систем, изменяющих изображение на сетчатке на неперевернутое, человек теряет способность адекватного зрительного восприятия. Через несколько дней использования таковой системой зрительная информация вновь начинает восприниматься нормально.

2. Сетчатка разбита на две приблизительно равные области, нервные волокна от которых идут в различные полушария мозга . Невзирая на то, что граница раздела приходится на центр зрительного поля, изображение не воспринимается как разорванное на две части.

3. Наличие на сетчатке “слепого пятна” (области, лишенной светочувствительных клеток) не приводит к появлению незаполненной области в зрительной картине даже при восприятии ее одним глазом.

4. чувство большого непрерывного вида строится из 2-ух не совпадающих друг с другом мозаичных картин, возникающих на сетчатках глаз.

5. Способность определения образов трехмерных объектов по их плоским контурным изображениям и возможность их систематизации.

Крайняя, может быть более умопомрачительная способность зрения человека, тесновато связана с активно разрабатываемой в арифметике и технике неувязкой определения образов.

Фурье-анализ изображений. При попадании в поле зрения человека новейшего объекта, его зрительный образ в сознании возникает очень стремительно, но позже уточняется и достраивается (время от времени с исправлением ошибок начального восприятия (все любители сбора грибов знают, как “замирает глаза функции I(x,y) в пространственный ряд Фурье, Его предстоящий анализ начинается с более неспешных пространственных гармоник и состоит в сопоставлении их амплитуд с “лежащей в памяти библиотекой образов”. По результатам анализа сравнимо маленького числа гармоник делается подготовительный вывод о объекте, который потом уточняется в итоге анализа высших составляющих. вместе с “волновой” существует и “точечная” теория восприятия зрительных образов, согласно которой изображение воспринимается как совокупа светящихся точек.

Т.о. даже на уровне традиционного описания исходя из убеждений арифметики нет принципной различия меж корпускулярным и волновым подходами к описанию действительности. Различие состоит в выборе набора базовых функций. Правильной формулировкой вопросца к естествознанию в рассматриваемом блоке заморочек, по-видимому заключается в том, есть ли в природе настоящие объекты, характеристики которых близки (либо даже тождественны) свойствам раздельно взятой базовой функции (гармонической либо дельта-функции). Традиционное естествознание отвечало на так поставленный вопросец утвердительно.

]]>