Учебная работа. Реферат: Основы фрактального исчисления

Учебная работа. Реферат: Основы фрактального исчисления

Базы
фрактального
исчисления

БалхановВасилийКарлович

Предложенасистемааксиом, определяющиефрактальноеисчисление. Показаноееприменениедляиерархическихструктур. Вкачествефрактальныхразветвленныхструктуррассмотреныдельтырекистримерныеканалы. Введеныфрактальныеинтегралыидифференциалы, вычисленыихзначениядляэлементарныхфункций. Рассмотреныпростейшиефрактальныеуравнения.

Введение во фрактальное исчисление. Фрактальная геометрия, сделанная Бенуа Б. Мандельбротом 30 лет вспять, основывается на экспериментальном факте, что в общем случае длина L случайной кривой (которая быть может изломана в хоть какой точке) степенным образом зависит от масштаба измерения d [1,2,3]:

L = C×d1-
D
. (1)

тут С — размерный множитель, собственный для каждой кривой, D — фрактальная размерность; приятный пример — длинноногому дорога будет казаться короче. Для обыденных, гладких линий D = 1 и получаем «настоящую» длину. Если кривая плотно заполняет всю плоскость (обычной пример — броуновская линия движения), то для нее D = 2. Формулу просто проверить, нарисовав синусоподобную линию и, меняя раствор циркуля, измерить длину таковой полосы. Достаточно разумеется, что как вся линия, так и хоть какой ее участок владеют одной и той же фрактальной размерностью. Такое свойство именуется самоподобием (скейлинг, масштабная инвариантность). Самоподобие значит, что как вся линия, так и хоть какой ее участок владеют одной и той же фрактальной размерностью. Если линию прирастить в l раз, то для измерения новейшей длины lL довольно применять масштаб, равный ld , т.е.

lL = C×( ld ) 1-
D
. (2)

Формулы Мандельброта и условие самоподобия в форме (2) довольно взять в виде аксиом фрактального исчисления, тогда чисто логическим методом можно получить фактически все, известные на крайнее время, результаты [4].

Другая формулировка. При решении разных задач бывает полезным отдать другую формулировку начальных аксиом. Во первых, длину определяют, подсчитывая число масштабов, т.е. L = N ( d )×d , где N (d ) — нужное число шагов (смесей циркуля), с которым масштаб обходит всю линию, при всем этом из (1) следует, что N ( d ) = C×d-
D
. В новеньком масштабе, равном

d*
= ×ld, (3)

длина будет L*
= C×d*
1-
D
. Подставляя (3) в выражение для L*
, получаем

L*
= C×l1-
D
×d 1-
D
. Но тут C×d 1-
D
есть начальная длина, равная N ( d )×d, как следует

L*
= l1-D
× N ( d )×d . (4)

С иной стороны, L*
= N (d*
)×d*
, либо L*
= N ( l×d ) ×l×d . Сравнивая крайний итог с (4), приходим к восхитительному результату:

N ( l×d ) = l-D
× N ( d ). (5)

В таком виде обычно и записывают условие самоподобия, подразумевая под N всякую функцию от собственных аргументов с хорошим от D показателем. Во вторых, в формуле (3) l и d входят равным образом, т.е. переобозначение ld не меняет вида самой формулы. Можно считать l масштабом, а d — масштабным множителем. Это просто осознать — чтоб измерить шестиметровую длину, необходимо двухметровый идеал приложить трижды, а можно трехметровый идеал приложить всего дважды. Заместо предложенных постулатов в базу теории фракталов можно положить симметрию переобозначения l и d и условие самоподобия в форме (5). Таковая формулировка может оказаться более подходящей в неких приложениях. Покажем это на примере иерархических структур, которые строятся по заблаговременно определенным правилам.

Иерархические структуры. Пусть у нас имеется некий единичный отрезок. Если взять этот отрезок за масштаб, то крайний уложится лишь один раз, т.е. N (d ) = 1. Дальше строим триадную кривую Коха. Для этого отрезок разбиваем на три равные части и на месте среднего из их строим «шапку». Тогда масштаб будет

d / 3, и его нужно будет приложить четыре раза, чтоб обойти новейшую длину, т.е.

N (d /3) = 4. Сравнивая крайнее соотношение с 4N (d ) = 4, заключаем, что 4N (d ) =

N (d /3). Это функциональное уравнение, и его решением будет степенная функция:

N ( d ) = C×d-
D
, где D = Ln 4/Ln 3, — разыскиваемая фрактальная размерность кривой Коха. В качестве последующего примера разглядим геометрический ряд: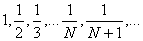. Расстояние меж примыкающими членами ряда будет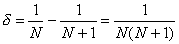, либо, при

N>> 1: d~ 1/ N 2
. Откуда N~d-1/ 2
, сравнивая с N~d-
D
, находим фрактальную размерность геометрического ряда: D = 1/2. Схожим образом можно разглядывать фактически все иерархические структуры.

Разветвленные структуры. Принципиальным примером внедрения фрактального исчисления является рассмотрение фрактальных разветвленных структур, к которым относятся дельты рек Селенги и Волги, стримерные каналы, образующиеся при коронном разряде в диэлектрических подложках, к крайним относятся и молнии в атмосфере Земли. Для построения разветвленных структур возьмем фрактальную линию и разрежем ее на огромное количество неравномерных отрезков. Разбросав эти отрезки по плоскости, мы получим пример разветвленной структуры. Наши постулаты разрешают найти зависимость длины всех отрезков от размера области, занимаемые отрезками на плоскости. Для этого проведем операцию переобозначения, заменив l на 1/R, где R будет линейным размером области. Тогда из (2), опосля обычных сокращений, получаем L = C×d1-
D
×RD
. Убрав все неопределенные масштабные множители, находим

L ~ R D
. (6)

Это принципиальный итог. Если принять, что все отрезки владеют однородной массовой плотностью, то их общая масса будет зависеть от размера области как RD
, а это известное положение в физике фрактальных кластеров, где оно и служит определением размерности [1,2].

В качестве примера разветвленной структуры была рассмотрена дельта реки Селенга. При расчете использовались топографическая и электрическая карты [5,6]. методика подсчета длины всех русловых рукавов и размеров областей разбиения тщательно изложены в [7,8]. Оказалось, что фрактальная размерность дельты Селенги равна 1.38 ¦ 0.01. Относительно маленькое

Кроме определения фрактальной размерности по формуле (3), была применена 2-ая независящая методика, основанная на последующем. Если посчитать число пересечений N руслами рукавов случайного периметра линейным размером R, то они соединены меж собой степенным образом:

N ~ R n
, n = 2 ( D — 1 ). (7)

Отменно итог можно доказать последующим образом. Для обыденных евклидовых линий число N не обязано зависеть от R, т.е. при D = 1 обязано быть n = 0. Если линия заполняет всю плоскость, т.е. D = 2, то N будет квадратично зависеть от области, т.е. n = 2. Предполагая линейную зависимость меж n и D, приходим к результату (7). При наиболее серьезном подходе нужно было бы применять понятие фрактальной производной [4]. В качестве примера приведем фрактальную производную от степенной функции:

.

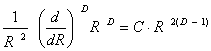А именно, приобретенная формула дозволяет отдать геометрическую интерпретацию фрактальной производной: так, для обыкновенной производной из площади круга получают длину окружности, а фрактальной производной из длины RD
получают канторовское огромное количество R2 (
D
— 1 )
. Само число всех пересечений представляет пример канторовского огромного количества. По данной нам методике для дельты Селенги было получено n = 0.74, и для дельты Волги n = 1.44. Используя эти значения, находим D = 1 + n / 2 = 1.37 и D = 1.72 для Селенги и Волги соответственно, что согласуются с выше приведенными значениями. Заметим, что методически создавать подсчет по формуле (7) много легче, чем применять (6). В качестве иллюстрации была рассчитана фрактальная размерность плоскостной проекции микроразрядов в фотопластинке (стримерные каналы), изображение которых представлена на рис. 2 в [10]. тут оказалось

n = 0.768 ¦ 0.008 и D = 1 + n / 2 = 1.38 ¦ 0.01.

Фрактальное исчисление. По определению, длина есть сумма всех масштабов, т.е.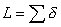, где сумма берется от 1 до N ( d ). Так как априори считается N>> 1, то сумму можно поменять неким интегралом, который назовем фрактальным, а метод его вычисления — фрактальным исчислением. Итак, определяем

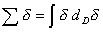. (8)

Обратим внимание на то, что значок D, указывающий на фрактальную размерность, пишется снизу дифференциала d. Так как длина фрактальной полосы есть C×d 1-
D
, то приходим к последующему, первому правилу фрактального исчисления — правилу интегрирования линейной функции:

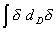= C×d 1-
D
. (9)

Проведем в данной нам формуле масштабное преобразование: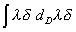 = C×(ld) 1-
D
. Выражение справа есть l1-
D
×C×d 1-
D
, либо, с учетом (9), l1-
D
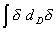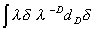× =. Сравнивая с начальным выражением, приходим к последующему закону для фрактального дифференциала:

.

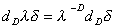В этом выражении ясно видно отличие фрактального дифференциала от дифференциала дробного порядка [11], для крайнего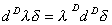. В общем случае для степенной функции можно получить последующее правило фрактального интегрирования:

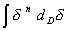= C ×d n-D
. (10)

Простые функции. Фрактальный интеграл от степенной функции выходит тривиально. Для этого в выражении (10) довольно переобозначить d на x:

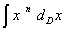= C × x n-D
. (11)

Для вычисления фрактального интеграла от экспоненциальной функции экспоненту нужно разложить в ряд, дальше применяя для всякого члена ряда формулу (11), совсем получаем

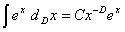. (12)

Лицезреем, что экспонента опосля фрактального интегрирования заполучила нелинейный множитель. Неизменные интегрирования тут не выписываем, если судить по дробному интегродифференциальному исчислению [11], вопросец о неизменной интегрирования неоднозначен. Интегрирование от тригонометрических функций продемонстрируем на синусе. Представляя функцию синус в экспоненциальной форме и применяя итог (12), в итоге получаем

В этом выражении просто выяснить одно из слагаемых в ряде, представляющей нигде не дифференцируемую функцию Вейерштрасса [1,2].

Фрактальное дифференцирование. Как и в обыкновенном случае, будем считать, что фрактальное дифференцирование — это оборотная к интегрированию операция. Таковым образом, полагаем, что

.

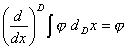сейчас просто можно установить правила фрактального дифференцирования простых функций. Опуская обыкновенные вычисления, приведем результаты:

,

,

.

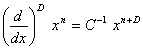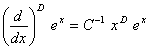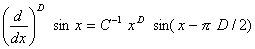Фрактальные уравнения. Для описания действий, происходящих в Природе, употребляют дифференциальные уравнения — 2-ой законНьютона, уравнения Максвелла и т.д. В истинное время непонятно, в которой форме должны смотреться законы движения в форме фрактальных производных. Потому приведем некие вероятные виды фрактальных уравнений и их легкие решения. Конкретно:

,

,

, .

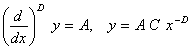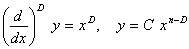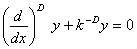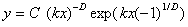В данной нам части практически завершено построение математического аппарата фрактального исчисления. Предстоящее развитие обязано пойти по пути внедрения к определенным задачкам, по пути совершенствования технических приемов.

Перечень литературы

Федер Е. Фракталы. — М.: мир, 1991, 254 с.

Шредер М. Фракталы, хаос, степенные законы. — Ижевск: НИЦ «Постоянная и хаотическая динамика», 2001, 528 с.

Божокин С.В., Паршин Д.А. Фракталы и мультифракталы. — Ижевск: НИЦ «Постоянная и хаотическая динамика», 2001, 128 с.

Балханов В.К. Введение в теорию фрактального исчисления. — Улан-Удэ.: Изд. Бурятского гос. ун-та, 2001, 58 с.

Топографическая карта, масштаб 1: 200000, лист ¦ 48-XXXV.

CD — диск «ГИС района дельты реки Селенги в пакете ArcView 2.3».

Балханов В.К. Дельта реки Селенга // Математика, вып. 3, 2002. Изд-во Бурятского гос. ун-та, Улан-Удэ. С. 13-18.

Балханов В.К., Башкуев Ю.Б. Фрактальные разветвленные структуры. Дельта реки Селенга // Горный информационно — аналитический бюллетень, 2002. N 4. С. 20-23.

Алексеевский Н.И., Соколова Ю.В. структура сети водотоков в русловых и дельтовых разветвлениях и методы ее формализации // Вестник Столичного ун-та, Серия 5, География, ¦ 2, 1999. С.13-19.

Попов Н.А. исследование пространственной структуры ветвящихся стримерных каналов коронного разряда // Физика плазмы, 2002, том 28, ¦ 7, с. 664-672.

Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некие их приложения. — Минск: Наука и техника, 1987. 688 с.

]]>