Учебная работа. Реферат: Построение поверхностей в Mathcad и Maple

Учебная работа. Реферат: Построение поверхностей в Mathcad и Maple

Mathcad. Построение поверхностей.

Резвое построение

Резвое построение является более легким методом построения поверхностей. Для этого нужно:

1. На лист Mathcad ввести формулу z(x,y):=…;

2. Избрать команду головного меню «Вставка», «График», избрать вид графика «поверхность» на панели инструментов «Графики».

3. В шаблон трехмерного графика ввести имя функции без указания аргументов.

Пример:

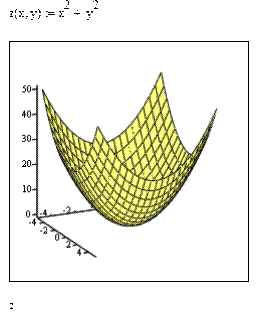
Построение поверхностей по матрице аппликат.

Самый «верный» метод построения графика поверхности, данной функцией от 2-ух переменных z = f(x,y), является наполнение матрицы значениями данной функции. При всем этом строчки и столбцы матрицы интерпретируются как абсциссы и ординаты. Пример:

Определение функции от 2-ух переменных z(x,y):=cos (x .
y)

Число линий для построения графика и масштаба N:=40 M:=40

Определение индексов i:=0..N j:=0..N

Определение массивов абсцисс и ординат xi
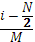:= yj
:=

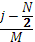
Определение массива аппликат Ai
,
j,
:= z(xi
, yj
)

В шаблон трехмерного графика вводим заглавие массива аппликат:

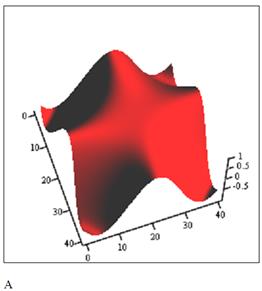
Построение при помощи функции CreateMesh.

Функция CreateMesh относится к группы Vectorandmatrix (Векторы и матрицы), потому что результатом работы функции будет матрица координат.

Формат вызова функции:

CreateMesh(F , x1, x2, y1, y2, xgrid, ygrid, mesh).

характеристики функции CreateMesh:

Mesh – количество линий в сетке функции;

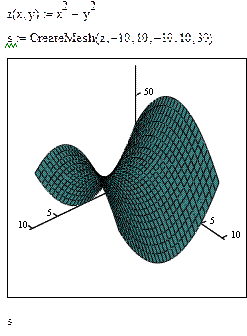F – вид функции (быть может либо формула, либо трёхмерный вектор, задающий каждую координату в параметрической форме, либо три отдельные функции, задающие координаты в параметрическом виде);

— x1 – нижняя граница переменной x;

— x2 – верхняя граница переменной x;

— y1 – нижняя граница переменной y;

— y2 – верхняя граница переменной y;

— xgrid – количество точек переменной х;

— ygrid – количество точек переменной y.

Пример:

В одной системе координат можно выстроить несколько поверхностей, для этого довольно найти их, а потом в шаблон графика ввести их имена без аргументов через запятую:

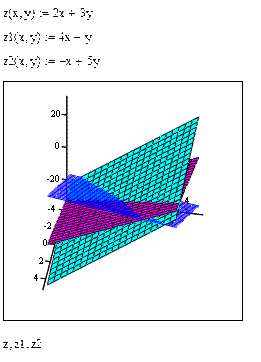
Построение 1-го и такого же графика в декартовой, цилиндрической

и сферической системах координат

Пусть задана какая-нибудь функция, к примеру z(x,y)=const. В разных системах координат эта функция имеет разные графики. В декартовой системе координат это плоскость, параллельная плоскости Оху, в цилиндрической – прямой радиальный цилиндр с основанием радиуса const, в сферической – шар радиуса const. Для конфигурации системы координат, нужно по шаблону графика щелкнуть правой клавишей мыши, в показавшемся списке избрать «Характеристики», потом «Данные QuickPlot» и указать подходящую систему координат. Пример:

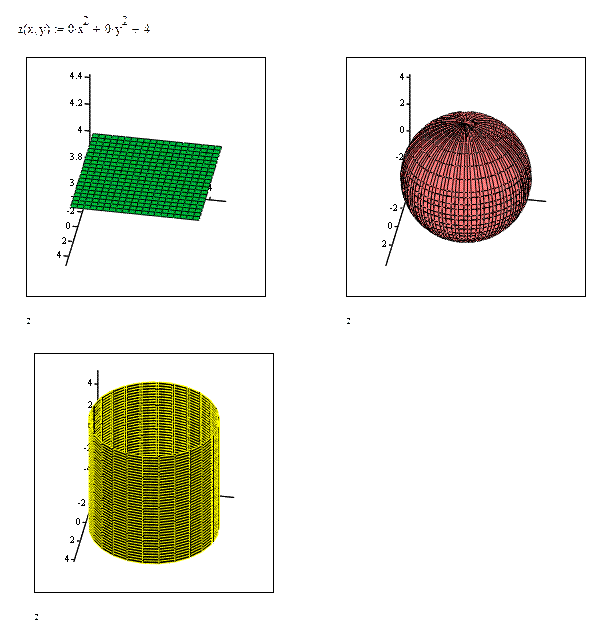
Построение полиэдров

Для построения полиэдров в Mathcad есть функция Polyhedron. Её можно употреблять 2-мя методами:

1) по имени, тогда воззвание к функции будет Polyhedron(“имя полиэдра”);

2) по коду, тогда воззвание к функции будет Polyhedron(“#номер полиэдра”).

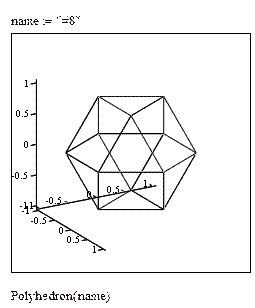
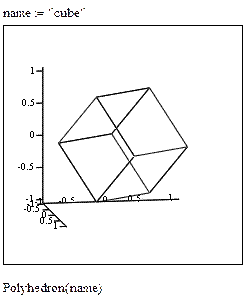
Построение поверхностей вращения.

Для построения поверхностей вращения в Mathcad комфортно употреблять функцию CreateMesh.

характеристики функции CreateMesh:

— x1, y1,z1 – матрицы значений для каждой координаты;

— -5 – нижняя граница переменной u;

— 5 – верхняя граница переменной u;

— 0 – нижняя граница переменной v;

— 2π – верхняя граница переменной v;

— 30 – количество линий в сетке графика.

Параметрические уравнения для поворота вокруг оси Ох:

x1(x,φ):=x

y1(x,φ):=y(x) .
cos(φ)

z1(x,φ):=y(x) .
sin(φ)

Параметрические уравнения для поворота вокруг оси Oy:

х2(x,φ):=x.
cos(φ)

у2(x,φ):=у(x)

z2(x,φ):=x.
sin(φ)

Пример: разглядим гиперболу y2
– x2
= 1. При вращении данной гиперболы вокруг оси Ох выходит однополостный гиперболоид, при вращении вокруг оси Оу – двуполостный гиперболоид. Построим эти поверхности вращения:

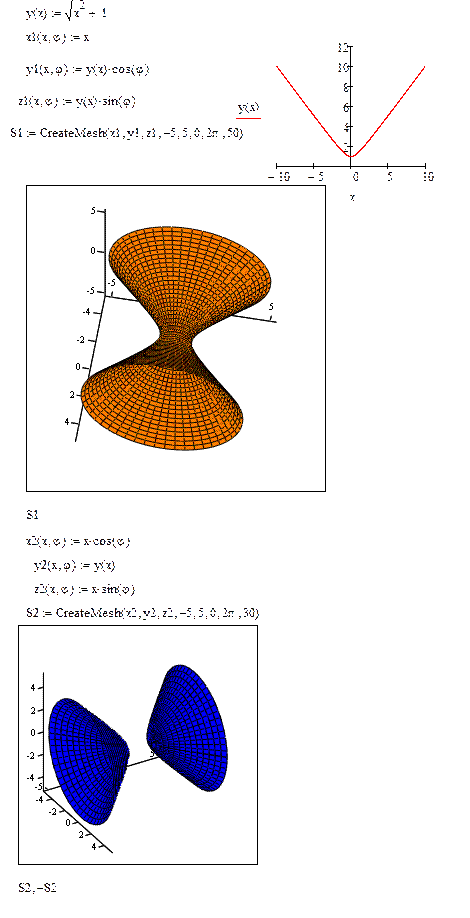
Построение пространственных линий.

Линия в пространстве, рассматриваемая как след передвигающейся точки, представляется системой трёх уравнений: x = x(t); y = y(t); z = z(t), выражающих координаты точки t. Эти уравнения именуются параметрическими уравнениями пространственной полосы. Для построения пространственных линий в Mathcad существует функция CreateSpace.

Функция CreateSpace относится к группы Vector and matrix (Векторы и матрицы), потому что результатом работы функции будет матрица координат. Работает аналогично CreateMesh. основное отличие в том, что параметрические уравнения должны быть функциями одной переменной, а не 2-ух, как в CreateMesh. Вызов функции: CreateSpace(F, t1, t2, tgrid). характеристики функции:

— F – вектор параметрических уравнений координат;

— t1 – нижняя граница переменной;

— t2 – верхняя граница переменной;

— tgrid – число линий сетки; не неотклонимый параметр; чем больше этот параметр, тем наиболее гладкая выходит линия; если он не довольно велик, линия выходит с изломами.

Пример:

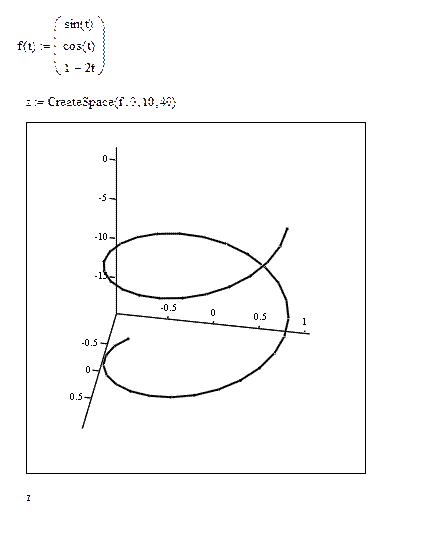
Maple. Построение поверхностей и пространственных линий.

График поверхности, данной очевидной функцией.

График функции 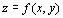можно нарисовать, используя команду plot3d(f(x,y), x=x1…x2, y=y1…y2, options)
. характеристики данной команды отчасти совпадают с параметрами команды plot. К нередко применяемым характеристикам команды plot3d
относится light=[angl1, angl2, c1, c2, c3]
– задание подсветки поверхности, создаваемой источником света из точки со сферическими координатами (angl1
, angl2
). цвет определяется толиками красноватого (c1
), зеленоватого (c2
) и голубого (c3
) цветов, которые находятся в интервале [0,1]. Параметр style=opt
задает стиль рисунка:
–точки, LINE
– полосы, HIDDEN
– сетка с удалением невидимых линий, PATCH
– заполнитель (установлен по дефлоту), WIREFRAME
– сетка с выводом невидимых линий, CONTOUR
– полосы уровня, PATCHCONTOUR
– заполнитель и полосы уровня. Параметр shading=opt
задает функцию интенсивности заполнителя, его xyz
– по дефлоту, NONE
– без раскраски.

Привер: построим поверхность x2
+ 4z = 4. Потому что z в первой степени, то его можно выразить и создать функцию очевидной, получим, z = . Вводимв Maple:

with (plots) : plot3d({ + 0 .
y2
}, x=-5..5, y = -5..5, grid = [25,25], axes=NORMAL)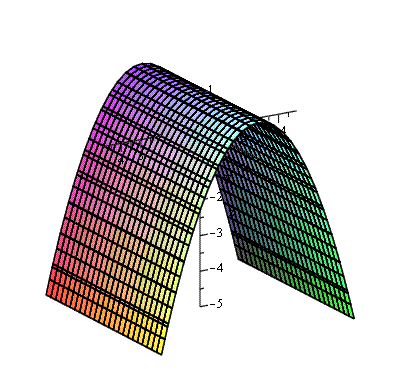

График поверхности, данной неявно.

Трехмерный график поверхности, данной неявно уравнением 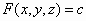, строится при помощи команды пакета plot: implicitplot3d(F(x,y,z)=c, x=x1..x2, y=y1..y2, z=z1..z2),
где указывается уравнение поверхности 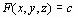и размеры рисунка по координатным осям.

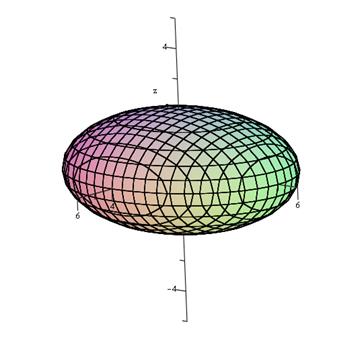Пример: построим поверхность 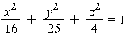Разумеется, что функция задана неявно, потому используем метод, описанный чуть повыше.

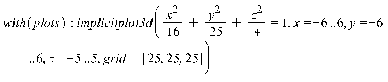
График поверхности, данной параметрически.

Если требуется выстроить поверхность, заданную параметрически:
=
(
,
),
=
(
,
),
=
(
,
), то эти функции перечисляются в квадратных скобках в команде: plot3d([x(u,v), y(u,v), z(u,v)], u=u1..u2, v=v1..v2)
.

Пример: выстроить поверхность заданную параметрически: х = 2.
u + v, y= v.
cos(u),

z = v.
sin(u). Для начала зададим функции Х0, Y0, Z0, надлежащие функциям х, у, z.

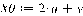
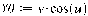
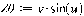
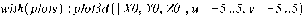
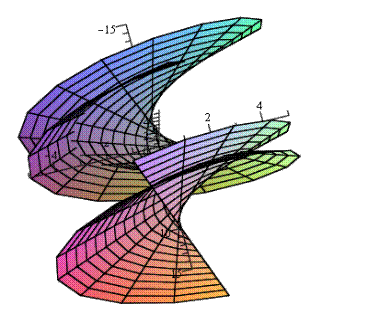
График пространственных кривых.

В пакете plot
имеется команда spacecurve
для построения пространственной кривой, данной параметрически: 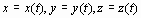. характеристики команды:
spacecurve([x(t),y(t),z(t)],t=t1..t2)
, где переменная t
меняется от t1
до t2
.

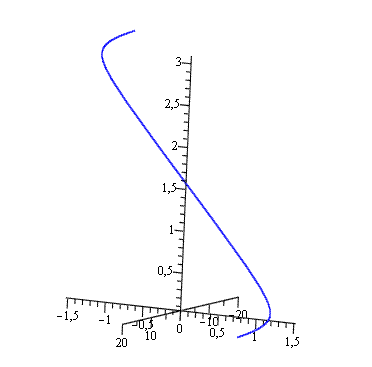
Пример: выстроить пространственную кривую, заданную параметрически х = arctg(t),

y = arcctg(t), z = t.

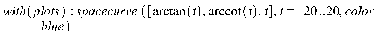
В Maple также существует возможность построения нескольких графиков сразу. Для этого нужно задать каждую поверхность, а потом употреблять команду display. Пример:

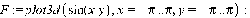
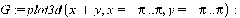
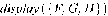
поверхность вращения.

Для построения поверхностей вращения в Maple есть функция Surface of revolution. Чтоб ей пользоваться необходимо во вкладке «Tools» избрать раздел «Tutors», потом подраздел «Сalculus – SingleVariablе», функцию «Surface of revolution». В показавшемся окне нужно ввести функцию, интервал на котором будет произведено построение, избрать ось вращения и характеристики графика. Окно графика возникает при нажатии клавиши «Close».

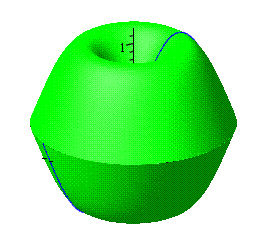
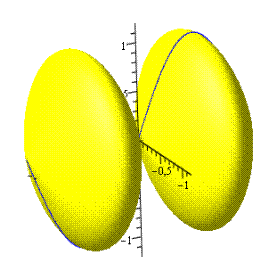
Пример: построим поверхности, приобретенные вращением графика функции y=sin x на интервале от 0 до π вокруг оси Ох и Оу. Вызываем функцию Surface of revolution как описано выше. В поле «f(x)» вводим sin(x), указываем границы интервала, в поле Line of Revolution в одном случае избираем Vertical, в другом Horizontal, жмем Сlose.

Федеральное агентство по образованию

Государственное образовательное учреждение высшего проф образования

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ технический УНИВЕРСИТЕТ

(ВолгГТУ)

Кафедра прикладной арифметики

Семестровая работа за I семестр

по информатике

Тема: «Построение трехмерных графиков в Mathcad и Maple»

Выполнил: студент группы ХТ-142 Долгачев А. С.

Проверил: Волчков В. М.

Оценка работы _________________ баллов

Волгоград, 2010 г.

]]>