Учебная работа. Реферат: Применение теории графов в информатике 2

Учебная работа. Реферат: Применение теории графов в информатике 2

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

КАФЕДРА АВТОМАТИЗИРОВАННОЙ ОБРАБОТКИ ЭКОНОМИЧЕСКОЙ инфы

КУРСОВАЯ РАБОТА

по дисциплине «Информатика»

на тему «Применение теории графов в информатике»

Исполнитель:

специальность

группа

№ зачетной книги

Управляющий:

Туймазы – 2007

Содержание

Введение. 3

1. Теоретическая часть. 4

1.1 История появления теории графов. 4

1.2 Главные понятия теории графов. 6

1.3 Главные аксиомы теории графов. 9

1.4 методы представления графов в компе. 14

1.4.1 Требования к представлению графов. 14

1.4.2 Матрица смежности. 14

1.4.3 Матрица инциденций. 15

1.4.4 Списки смежности. 15

1.4.5 Массив дуг. 15

1.5 Обзор задач теории графов. 16

Заключение. 17

2. Практическая часть. 18

2.1. Общая черта задачки. 18

2.2. Описание метода решения задачки. 19

Перечень использованной литературы.. 24

Введение

Если вы любите решать олимпиадные задачки, то, наверняка, не раз составляли таблицы, изображали объекты точками, соединяли их отрезками либо стрелками, подмечали закономерности у приобретенных рисунков, делали над точками и отрезками операции, не похожие на арифметические, алгебраические либо на преобразования в геометрии. Другими словами для вас приходилось строить математический аппарат специально для решения задачки. А это значит, что вы открывали себе начала теории графов. Исторически сложилось так, что теория графов зародилась двести с излишним лет вспять конкретно в процессе решения головоломок. Весьма длительно она находилась в стороне от основных направлений исследовательских работ ученых, была в королевстве арифметики на положении Золушки, чьи дарования открылись полностью только тогда, когда она оказалась в центре общего внимания.

1. Теоретическая часть

1.1 История появления теории графов

Родоначальником теории графов принято считать математика Леонарда Эйлера (1707-1783) [3, стр. 36]. Но теория графов неоднократно переоткрывалась различными создателями при решении разных прикладных задач.

1.
На рис. 1 представлен схематический план центральной части городка Кенигсберг (сейчас Калининград), включающий два берега реки Перголя, два острова в ней и семь соединяющих мостов. задачка заключается в том, чтоб обойти все четыре части суши, пройдя по любому мосту один раз, и возвратиться в начальную точку. Эта задачка была решена (показано, что решение не существует) Эйлером в 1736 году.

Набросок 1

2.
Имеется три дома и три колодца, каким-то образом расположенные на плоскости. Провести от всякого дома к любому колодцу тропинку так, чтоб тропинки не пересекались (рис. 2). Эта задачка была решена (показано, что решение не существует) Куратовским в 1930 году [2, стр. 51].

Набросок 2

3.
Разбиение на плоскости на непересекающиеся области именуется картой. Области на карте именуются примыкающими, если они имеют общую границу. задачка состоит в раскрашивании карты таковым образом, чтоб никакие две примыкающие области не были закрашены одним цветом (рис. 3). С конца позапрошлого века известна догадка, что для этого довольно 4 красок. В 1976 году Аппель и Хейкен выпустили решение задачки о 4 красках, которое базировалось на переборе вариантов при помощи компа. Решение данной нам задачки «программным методом» явилось прецедентом, породившим бурную дискуссию, которая никак не закончена. Сущность размещенного решения заключается в том, чтоб перебрать огромное, но конечное число (около 2000) типов возможных контрпримеров к аксиоме о 4 красках и показать, что ни один вариант контрпримером не является. Этот перебор был выполнен программкой приблизительно за тыщу часов работы суперкомпьютера. Проверить «вручную» приобретенное решение нереально – размер перебора выходит далековато за рамки человечьих способностей. Почти все арифметики ставят вопросец: можно ли считать такое «программное подтверждение» реальным подтверждением? Ведь в программке могут быть ошибки… способы формального подтверждения корректности программ не применимы к программкам таковой трудности, как обсуждаемая. Тестирование не может гарантировать отсутствие ошибок и в данном случае совершенно нереально. Таковым образом, остается надеяться на программистскую квалификацию создателей и веровать, что они создали все верно.

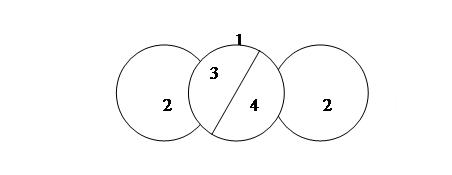
Набросок 3

1.2 Главные понятия теории графов

1)






именуется совокупа 2-ух множеств – непустого огромного количества V(огромного количества вершин) и огромного количества E двухэлементных подмножеств огромного количества V(E – огромное количество ребер).

2)
именуется граф, в каком 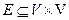— огромное количество упорядоченных пар вершин вида (x,y), где x именуется началом, а y – концом дуги. Дугу (x, y) нередко записывают как 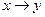. молвят также, что дуга 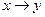ведет от верхушки x к верхушке y, а верхушка y
с верхушкой x.

3) Если элементом огромного количества E быть может пара
(не разных) частей V, то таковой элемент огромного количества E именуется
, а граф именуется
(либо
).

4) Если E является не обилием, а
, содержащим несколько схожих частей, то эти элементы именуются
, а граф именуется
.

5) Если элементами огромного количества E являются не непременно двухэлементные, алюбые подмножества огромного количества V, то такие элементы огромного количества E именуются
, а граф именуется
.

6) Если задана функция




и/либо




, то огромное количество
именуется обилием
, а граф именуется
(либо
). В качестве огромного количества пометок обычно употребляются буковкы либо целые числа. Если функция
инъективна, другими словами различные верхушки (ребра)имеют различные пометки, то граф именуют
.

7)
именуется граф G′(V′,E′), где 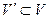и/либо .

a) Если V′ = V, то G′ именуется
подграфом G.

b) Если 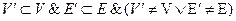, то граф G′ именуется
подграфом графа G.

c) Подграф G′(V′,E′) именуется правильным подграфом графа G(V,E), если G′ содержит все вероятные рёбра G.

8)
верхушки – это количество ребер, инцидентных данной нам верхушке (количество смежных с ней вершин).

9)
в графе именуется чередующаяся последовательность вершин и ребер 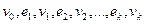, в какой любые два примыкающих элемента инциденты.

a) Если 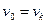, то маршрут
, по другому
.

b) Если все ребра различны, то маршрут именуется

c) Если все верхушки (а означает, и ребра) различны, то маршрут именуется
.

d) Замкнутая цепь именуется
.

e) Замкнутая обычная цепь именуется
.

f) Граф без циклов именуется

g) Для орграфов цепь именуется
, а цикл –
.

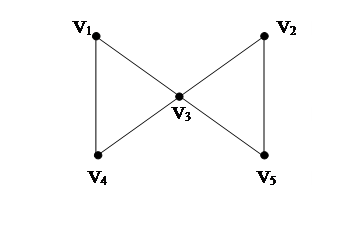
рис. 4. Маршруты, цепи, циклы

Пример

В графе, диаграмма которого приведена на рис.4:

1. v1
, v3
, v1
, v4
– маршрут, но не цепь;

2. v1
, v3
, v5
, v2
, v3
, v4
– цепь, но не обычная цепь;

3. v1
, v4
, v3
, v2
, v5
– обычная цепь;

4. v1
, v3
, v5
, v2
, v3
, v4
, v1
– цикл, но не обычной цикл;

5. v1
, v3
, v4
, v1
– обычной цикл.

10) Если граф имеет цикл (не непременно обычной), содержащий все ребра графа по одному разу, то таковой цикл именуется
циклом.

11) Если граф имеет обычной цикл, содержащий все верхушки графа (по одному разу), то таковой цикл именуется
циклом.

12)
именуется связный граф без циклов.

13)
именуется дерево, содержащее все верхушки графа.

14)
именуется огромное количество ребер, в каком никакие два не смежны.

15) Паросочетание именуется
, если никакое его надмножество не является независящим.

16) Две верхушки в графе
, если существует соединяющая их обычная цепь.

17) Граф, в каком все верхушки соединены, именуется

18) Граф, состоящий лишь из изолированных вершин, именуется

19)
именуется количество ребер в нем (с повторениями).

20)
меж верхушками u и v именуется длина кратчайшей цепи 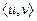, а сама кратчайшая цепь именуется
.

21)
графа G именуется длина длиннейшей геодезической.

22)
верхушки v в связном графе G(V,E) именуется наибольшее расстояние от верхушки v до остальных вершин графа G.

23)
графа G именуется меньший из эксцентриситетов вершин.

24) Верхушка v именуется
, если ее эксцентриситет совпадает с радиусом графа.

25) Огромное количество центральных вершин именуется
графа.

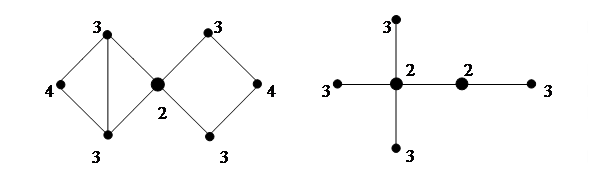
рис. 5 Эксцентриситеты вершин и центры графов (выделены).

1.3 Главные аксиомы теории графов

Делая упор на приведенные выше определения теории графов, приведем формулировки и подтверждения теорем, которые потом отыщут свои приложения при решении задач.

Аксиома 1.
Двойная сумма степеней вершин хоть какого графа равна числу его ребер. [
1, стр. 66]

подтверждение
. Пусть А1

, А2

, А3

, …,An


вер­шины данного графа, ap(
1

), p(А2

), …, p(An

) – степени этих вершин. Подсчитаем число ребер, сходящихся в каждой верхушке, и просуммируем эти числа. Это рав­носильно нахождению суммы степеней всех вершин. При таком подсчете каждое ребро будет учтено два раза (оно ведь постоянно соединяет две верхушки).

Отсюда следует: p(
1

)+p(А2

)+ … +p(An

)=0,5
либо 2(p(A1

)+p(
2

)+ … +p(An

))=
, где

число ребер.

Аксиома 2.
Число нечетных вершин хоть какого графа четно.

подтверждение
. Пусть
1



2



3


ak


это сте­пени четных вершин графа, а
1



2



3


bm


степени нечетных вершин графа. Сумма
1



2



3


ak



1



2



3


bm

ровнов дважды превосходит число ребер гра­фа. Сумма
1



2



3


ak

четная (как сумма четных чисел), тогда сумма
1



2



3


bm

обязана быть четной. Это может быть только в том случае, если

четное, другими словами четным является и число нечетных вершин графа. Что и требовалось обосновать.

Следствие 1.
Нечетное число знакомых в хоть какой компании всег­да четно.

Следствие 2.
Число вершин полиэдра, в каких сходится нечетное число ребер, четно.

Следствие
3. Число всех людей, когда-либо пожавших руку дру­гим людям, нечетное число раз, является четным.

Аксиома 3.
Во всяком графе с
верхушками, где
больше либо равно 2, постоянно найдутся две либо наиболее верхушки с оди­наковыми степенями.

подтверждение
. Если граф имеет
вершин, то любая из их может иметь степень 0, 1, 2, …, (
—
1). Представим, что в неком графе все его верхушки имеют различную степень, другими словами
и покажем, что этого быть не может. Вправду, если р(
)=0
то это означает, что
изолированная верхушка, и потому в графе не найдется верхушки
со степенью р(
)=
-1
В са­мом деле, эта верхушка обязана быть соединена с (

1) верхушкой, в том числе и с
, но ведь
оказалась изолированной. Как следует, в графе, имеющем n
вершин, не мо­гут быть сразу верхушки степени 0 и (
-1). Это означает, что из n
вершин найдутся две, имеющие однообразные степени.

Аксиома 4.
Если в графе с
верхушками (
больше либо равно 2) лишь одна пара имеет одинаковуюстепень, то в этом графе постоянно найдется или единственная изолированная верхушка, или единственная верхушка, соединенная со всеми иными.

подтверждение данной аксиомы мы опускаем. Остановимся только на неком ее пояснении. Содержание данной нам аксиомы отлично разъясняется задачей: группа, состоящая из
школьников, обменивается фото. В некий момент времени выяс­няется, что двое сделали однообразное число обме­нов. Обосновать, что посреди школьников есть или один еще не начинавший обмена, или один уже завершив­ший его.

Аксиома
5.
Если у графа все обыкновенные циклы четной длины, то он не содержит ни 1-го цикла четной длины.

Сущность аксиомы в том, что на этом графе нереально отыскать цикл (как обычной, так и сложный) нечетной длины, другими словами содержащий нечетное число ребер.

Аксиома 6.
Для того, чтоб граф был эйлеро­вым, нужно и довольно, чтоб он был связным и все его верхушки имели четную степень.

Аксиома 7.
Для того чтоб на связном графе можно было бы проложить цепь
содержащую все его ребра в точности по одному разу, нужно и довольно, чтоб
и
были единственными нечет­ными верхушками этого графа.

подтверждение данной нам аксиомы весьма любопытно и ха­рактерно для теории графов. Его также следует счи­тать конструктивным (обратите внимание на то, как применена при всем этом аксиома 3.6). Для подтверждения к начальному графу присоеди­няем ребро (
,
); опосля этого все верхушки графа станут четными. Этот новейший граф удовлетворяет всем условиям аксиомы 3.6, и потому в нем можно про­ложить эйлеров цикл
И если сейчас в этом цикле удалить ребро (
,
)
то остается разыскиваемая цепь АВ.

На этом любопытном приеме основано доказатель­ство последующей аксиомы, которую следует считать обоб­щением аксиомы 7.

Аксиома 8.
Если данный граф является связ­ным и имеет 2
вершин нечетной степени, то в нем можно провести
разных цепей, содержащих все его ребра в совокупы ровно по одному разу.

Аксиома 9.
Разных деревьев с
перенумерованными верхушками можно выстроить nn

-2

.

По поводу подтверждения данной нам аксиомы создадим одно замечание. Эта аксиома известна, в главном, как вывод британского математика А. Кэли (1821—1895). Графы-деревья давно завлекали внимание ученых. Се­годня двоичные деревья употребляются не только лишь ма­темами, а и биологами, химиками, физиками и инженерами (подробнее о этом – в параграфе 6).

Аксиома 10.
Полный граф с пятью верши­нами не является плоским.

подтверждение
. Воспользуемся формулой Эйлера:
=2
где
— число вершин плоского графа,
— число его ре­бер,
— число граней. Формула Эйлера справедлива для плоских связных графов, в каких ни один из многоугольников не лежит снутри другого.

Эту формулу можно обосновать способом математиче­ской индукции. Это подтверждение мы опускаем. За­метим лишь, что формула справедлива и для пространственных полиэдров. Пусть все 5 вершин графа соединены друг с дру­гом. Замечаем, что на графе нет ни одной грани, ограниченной лишь 2-мя ребрами. Если че­рез φ1

обозначить число таковых граней, то φ2

=0. Дальше рассуждаем от неприятного, а конкретно: пред­положим, что исследуемый граф тонкий. Это означает, что для него верна формула Эйлера. Число вершин в данном графе
=5
число ребер
=10, тогда число граней
=2-
+
=2-5+10=7.

Это число можно представить в виде суммы:
=φ1
+φ2
+φ3
+
…, где φ3

– число граней, ограниченных 3-мя ребрами, φ4

— число граней, ограниченных че­тырьмя ребрами и т. д.

С иной стороны, каждое ребро является границей 2-ух граней, а потому число граней равно 2
в то же время 2
=20=3φ3
+
4φ4

+…
. Умножив равенство
=7=φ3
+ φ4
+ φ5
+
…
на три, получим З
=21=3( φ3
+ φ4
+ φ5
+ …).

ясно, что (3φ3
+
3φ4

+3φ5

+…) < (3φ3
+
4φ4
+
5φ5
+
…

либо 3
<2
, но по условию, 2
=20, а З
=21; потому вывод, приобретенный при введенном нами предположе­нии (граф тонкий), противоречит условию. Отсюда заключаем, что полный граф с пятью верхушками не является плоским.

Аксиома 11. (Аксиома Понтрягина-Куратовского)
Граф является плоским и тогда лишь тогда, когда он не имеет в качестве подграфа полного графа с пятью верхушками.

В заключение этого параграфа, на наш взор, следует упомянуть то, что в нем объяснялись лишь главные аксиомы теории графов. Их практическое применение будет рассмотрено в последующих параграфах реферата.

1.4 методы представления графов в компе

Конструирование структур данных для представления в программке объектов математической модели – это база искусства практического программирования. Дальше приводится четыре разных базисных представления графов. Выбор лучшего представления определяется требованиями определенной задачки. Наиболее того, при решении определенных задач употребляются, как правило, некие композиции либо модификации обозначенных представлений, общее число которых неоглядно. Но они все так либо по другому основаны на тех базисных идеях, которые описаны в этом разделе.

1.4.1 Требования к представлению графов

Известны разные методы представления графов в памяти компа, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. задачки. Дальше приведены четыре более нередко применяемых представления с указанием свойства n(p,q) – размера памяти для всякого представления. тут p – число вершин, а q – число ребер.

1.4.2 Матрица смежности

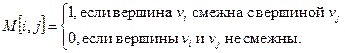
Для матрицы смежности n(p,q) = O(p2
).

Замечание

Матрица смежности неориентированного графа симметрична относительно главной диагонали, потому довольно хранить лишь верхнюю (либо нижнюю) треугольную матрицу.

1.4.3 Матрица инциденций

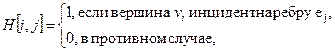
а для орграфа

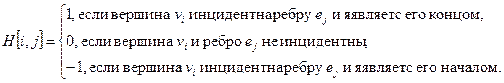
Для матрицы инциденций n(p,q) = O(pq).

1.4.4 Списки смежности

случае представления неориентированных графов перечнями смежности n(p,q) = O(p+2q), а в случае нацеленных графов n(p,q) = O(p+q).

1.4.5 Массив дуг

истории, лингвистике, соц науках, технике и т.п. Большей популярностью теоретико-графовые модели употребляются при исследовании коммуникационных сетей, систем информатики, хим и генетических структур, электронных цепей и остальных систем сетевой структуры.

Дальше перечислим некие типовые задачки теории графов и их приложения:

— Задачка о кратчайшей цепи

подмена оборудования

составление расписания движения тс

размещение пт скорой помощи

размещение телефонных станций

— задачка о наивысшем потоке

анализ пропускной возможности коммуникационной сети

организация движения в динамической сети

лучший подбор интенсивностей выполнения работ

синтез двухполюсной сети с данной структурной надежностью

задачка о распределении работ

— Задачка о упаковках и покрытиях

оптимизация структуры ПЗУ

размещение диспетчерских пт городской транспортной сети

— Раскраска в графах

распределение памяти в ЭВМ

проектирование сетей телевизионного вещания

— Связность графов и сетей

проектирование кратчайшей коммуникационной сети

синтез структурно-надежной сети циркуляционной связи

анализ надежности стохастических сетей связи

— Изоморфизм графов и сетей

структурный синтез линейных избирательных цепей

автоматизация контроля при проектировании БИС

— Изоморфное вхождение и пересечение графов

локализация неисправности при помощи алгоритмов поиска МИПГ

покрытие схемы данным набором типовых подсхем

— Автоморфизм графов

конструктивное перечисление структурных изомеров для производных органических соединений

синтез тестов цифровых устройств

Заключение

В работе были рассмотрены задачки из теории графов, которые уже стали традиционными. В особенности нередко в практическом программировании появляются вопросцы о построении кратчайшего остова графа и нахождении наибольшего паросочетания. Понятно также, что задачка о нахождении гамильтонова цикла принадлежит к числу NP-полных, т.е. действенный метод для ее решения не найден. Таковым образом, задачки теории графов животрепещущи, потому что могут принести экономию времени и средств на производстве и в быту.

2. Практическая часть

2.1. Общая черта задачки

Расмотрим последующую задачку:

1. Выстроить таблицы по приведенным данным о доходах членов семьи (табл. 1, 2) и о расходах семьи (табл. 3) за квартал.

Доходы Чижовой М. А. за 1 квартал 2006 г., руб.


Наименование доходов

Сентябрь

Октябрь

Ноябрь

Декабрь


Заработная плата
4000
3000
2200
3200

Остальные поступления
-
500
-
1000

Сумма дохода за месяц

Таблица 1 Доходы Чижовой М. А. за квартал

Доходы Чижова А. С. за 1 квартал 2006 г., руб.


Наименование доходов

Сентябрь

Октябрь

Ноябрь

Декабрь


Заработная плата
7200
7000
7500
7400

Остальные поступления
1200
500
500
1000

Сумма дохода за месяц

Таблица 2 Доходы Чижова А. С. за квартал

Расходы семьи Чижовых за 1 квартал 2006 г., руб.


Наименование расходов

Сентябрь

Октябрь

Ноябрь

Декабрь


Коммунальные платежи
630
670
700
800

Оплата электроэнергии
100
100
120
120

Оплата телефонных счетов
195
195
195
195

Расходы на питание
2500
2500
2600
3000

Остальные расходы
1000
1000
1500
2000

Погашение кредита
4000
4000
4000
4000

Суммарный расход за месяц

Таблица 3 Расходы семьи Чижовых за квартал

2. Заполнить таблицу 4 числовыми данными о доходах семьи за квартал, выполнив консалидацию по расположению данных.

Доходы семьи Чижовых за 1 квартал 2006 г., руб.


Наименование доходов

Сентябрь

Октябрь

Ноябрь

Декабрь


Заработная плата

Остальные поступления

Сумма дохода за месяц

Таблица 4 Доходы семьи Чижовых за квартал

3. Составить таблицу планирования бюджета семьи на квартал (табл. 5).

Бюджет семьи Чижовых за 1 квартал 2006 г., руб.


Наименование

Сентябрь

Октябрь

Ноябрь

Декабрь


Суммарный Доход за месяц

Суммарный расход за месяц

Остаток

Таблица 5 бюджет семьи Чижовых за квартал

4. По данным о бюджете семьи на квартал (табл. 5) выстроить гистограмму.

2.2. Описание метода решения задачки

1. Запустить табличный микропроцессор MS Excel.

2. Сделать книжку с именованием «Бюджет».

3. Лист 1 переименовать в лист с заглавием Доходы.

4. На рабочем листе Доходы
MSExcel сделать таблицы «Доходы Чижовой М. А. за квартал» и «Доходы Чижова А. С. за квартал».

5. Заполнить таблицы доходов начальными данными (рис. 2.1).

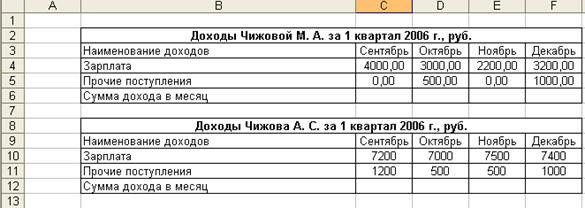
Набросок 2. 1 Размещение таблиц доходов на рабочем листе Доходы MS Excel

6. Лист 2 переименовать в лист с заглавием Расходы.

7. На рабочем листе Расходы
MS Excel сделать таблицу расходов семьи Чижовых за квартал.

8. Заполнить таблицу расходов начальными данными (рис. 2.2)

Набросок 2. 2 Размещение таблиц расходов на рабочем листе Расходы MS Excel

9. Заполнить строчку Сумма дохода за месяц
таблиц «Доходы Чижовой М. А. за 1 квартал 2006 г., руб.» и «Доходы Чижова А. С. за 1 квартал 2006 г., руб.», находящихся на листе Доходы
последующим образом:

Занести в ячейку С6 формулу:

=С4+С5

Размножить введенную в ячейку С6 формулу для других ячеек (с С4 по F4 и с С12 по F12) данных строк.

Таковым образом будет автоматом подсчитаны суммы дохода за месяц (рис. 2.3).

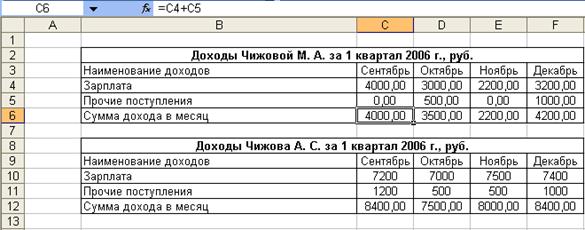
Набросок 2. 3 Автоматический подсчет суммы доходов за месяц

10. Заполнить строчку Суммарный расход за месяц
таблицы «Расходы семьи Чижовых за 1 квартал 2006 г., руб.», находящейся на листе Расходы
последующим образом:

Занести в ячейку С10 формулу:

=СУММ(C4:C9)

Размножить введенную в ячейку С10 формулу для других ячеек (с С10 по F10) данной строчки.

Таковым образом будет автоматом подсчитана сумма расхода за месяц (рис. 2.4).

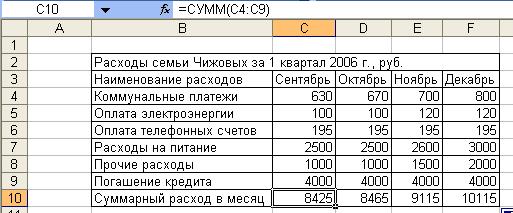
Набросок 2. 4 Автоматический подсчет суммы расходов за месяц

11. Лист 3 переименовать в лист с заглавием Итоги.

12. На рабочем листе Итоги
MS Excel сделать таблицу «Доходы семьи Чижовых за 1 квартал 2006 г., руб.»

13. Заполнить строчки Заработная плата, Остальные поступления, Сумма дохода за месяц
таблицы «Доходы семьи Чижовых за 1 квартал 2006 г., руб.», находящейся на листе Итоги
последующим образом:

Занести в ячейку С4 формулу:

=Доходы!C4+Доходы!C10

Размножить введенную в ячейку С4 формулу для других ячеек (с С4 по F6) данной таблицы.

Таковым образом будут автоматом подсчитана сумма дохода за месяц (рис. 2.5).

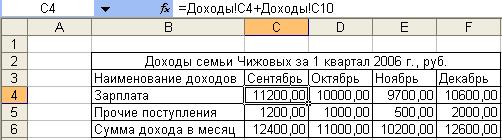
Набросок 2. 5 Автоматический подсчет суммы доходов за месяц

14. На рабочем листе Итоги
MS Excel сделать таблицу «Бюджет семьи Чижовых за 1 квартал 2006 г., руб.»

15. Заполнить строчку Суммарный Доход за месяц
таблицы «Бюджет семьи Чижовых за 1 квартал 2006 г., руб.», находящейся на листе Итоги
последующим образом:

Занести в ячейку С11 формулу:

=C6

Размножить введенную в ячейку С11 формулу для других ячеек (с С11 по F11) данной таблицы.

16. Заполнить строчку Суммарный расход за месяц
таблицы «Бюджет семьи Чижовых за 1 квартал 2006 г., руб.», находящейся на листе Итоги
последующим образом:

Занести в ячейку С12 формулу:

=Расходы!C10

Размножить введенную в ячейку С12 формулу для других ячеек (с С12 по F12) данной таблицы.

17. Заполнить строчку Остаток
таблицы «Бюджет семьи Чижовых за 1 квартал 2006 г., руб.», находящейся на листе Итоги
последующим образом:

Занести в ячейку С13 формулу:

=C11-C12

Размножить введенную в ячейку С13 формулу для других ячеек (с С13 по F13) данной таблицы.

Таковым образом будет заполнена таблица «Бюджет семьи Чижовых за 1 квартал 2006 г., руб.» (рис. 2.6)

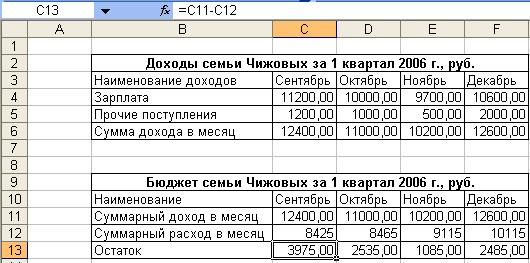
Набросок 2. 6 Автоматическое наполнение таблицы «Бюджет семьи Чижовых за 1 квартал 2006 г., руб.»

18. Лист 4 переименовать в лист с заглавием гистограмма.

19. По данным таблицы «Бюджет семьи Чижовых за 1 квартал 2006 г., руб.» на листе гистограмма
построим гистограмму (рис. 2.7).

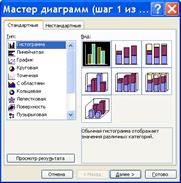
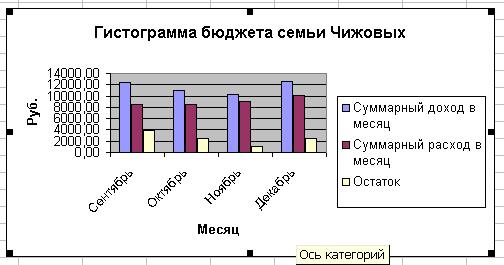
Набросок 2. 7 гистограмма

Перечень использованной литературы

1. Болтянский В.Г., Приятная топология, М., Просвещение, 1982.

2. Кордемский Б.А., Математическая находчивость, М., Физматгиз, 1954.

3. Кук Д., Бейз Г., Компьютерная математика, М., Наука, 1990.

4. Оре О., Графы и их применение, Новокузнецкий Физико-математический институт, 2000.

5. Информатика. Лабораторный практикум для студентов 2 курса всех специальностей. – М.: ВЗФЭИ, 2006.

]]>