Учебная работа. Реферат: Принципы квантовой механики

Учебная работа. Реферат: Принципы квантовой механики

Соотношение неопределенности Гейзенберга.

Логическим развитием идеи о корпускулярных свойствах света (“волны могут вести себя подобно частичкам”) явилось признание волновых параметров у частиц (электрон, нейтрон, протон и т.д. не достаточно различаются от фотонов и подобно им могут проявлять волновые характеристики).к примеру, в случае весьма близкого расположения маленьких щелей в опыте Юнга с источником электронов заместо светового так же возникает интерференционная картина. Рентгеновские лучи (фотоны с весьма большенный энергией) при дифракции на трехмерной кристаллической структуре дают картину, схожую с получающейся при дифракции электронов.

Рассуждения, подобные ранее проделанным для интерферирующих фотонов, требуют признания невозможности постановки опыта по выяснению через какое из 2-ух отверстий пропархал электрон при условии сохранения интерференционной картины. В отличие от фотона, электрон (либо иная простая частичка) в принципе могут быть зарегистрированы без их неотклонимого поглощения (к примеру, по рассеянному на их свету). Но, хоть какое взаимодействие владеющих малыми частиц с иными телами (даже со светом) безизбежно приводит к значимым изменениям состояний самих наблюдаемых частиц, что ведет к разрушению интерференционной картины (фотоны при рассеянии передают частичкам импульс порядка , попытка уменьшения которого за счет уменьшения частоты освещающего излучения безизбежно приводят к потере инфы о положении частички из-за явления дифракции). Бессчетные мысленные опыты, подобные рассмотренному приводят к выводу о невозможности одновременного измерения координаты и импульса частиц со сколь угодно высочайшей наперед данной точностью. Выражающее принципные ограничения на точность измерений неравенство, связывающее мало вероятные погрешности было предложено Гейзенбергом и носит заглавие соотношения неопределенности:

.

Соотношение неопределенности Гейзенберга явилось предметом пристального внимания философии, так как провозглашаемый принципный запрет перекликался с мыслями приверженцев агностических учений, отрицающих возможность зания окружающего нас мира. Невзирая на то, что подавляющее большая часть естествоиспытателей уверено в познаваемости мира, требовался суровый философский анализ появившейся препядствия. По-видимому, выход состоит в признании неприменимости способов описания макроскопических объектов к объектам микромира: если объект не владеет какими-либо чертами, то невозможности их четкого экспериментального определения совсем не значит невозможности исследования объекта (бессмысленность попыток получить экспериментально ответ на вопросец о длине хвоста черта не значит невозможности зания мира в целом). Т.о. соотношение неопределенности является “подсказкой” природы о том, что обычный язык традиционной кинематики и динамики Ньютона малопригоден для описания действий с ролью объектов микромира.

Индивидуальности квантово-механического описания. “Правила игры” квантовомеханического описания нерелятивистских макро- и микроскопичных объектов не могут быть выведены, исходя из “обычных” традиционных законов, так как являются наиболее общими и содержат в себе эти традиционные законы, как личный вариант, получаемый в виде чисто математических следствий из постулируемых принципов квантовой механики (принцип соответствия должен производиться).

Аспектом истинности формулируемых принципов, как обычно, является понятие случайности употребляется для описания поведения частей статистических ансамблей и является только сознательной жертвой полнотой описания во имя упрощения решения задачки. В микромире же четкий прогноз поведения объектов, дающий значения его обычных для традиционного описания характеристик, по-видимому, совершенно неосуществим. По этому поводу до сего времени ведутся оживленные дискуссии: приверженцы традиционного детерминизма, не отрицая способности использования уравнений квантовой механики для практических расчетов, лицезреют в учитываемой ими случайности итог нашего неполного осознания законов (“внутренних устройств”), управляющих пока непредсказуемым для нас поведением микро объектов. Приверженцем такового подхода, допускающего наличие у квантовых объектов “внутренних степеней свободы”, бал А. Эйнштейн, сформулировавших свою позицию в именитом выражении: ”Я не могу представить, что бы господь Бог играл в кости”. По сей день не найдено никаких экспериментальных фактов, указывающих на существование внутренних устройств, управляющих “случайным” поведением микрообъектов.

2. Принципно отличающийся от традиционного законсложения вероятностей взаимоисключающих друг дружку (с традиционной точки зрения) событий (к примеру, прохождение электрона через одну из щелей экрана в опыте Юнга). В традиционной концепции вероятности постоянно складываются:

(2) ,

что и приводит к не оправдывающемуся на опыте ожиданию найти при открывании 2-ух щелей картины, равную сумме изображений, получаемых от каждой из щелей в отдельности. В кавнтовой механике закон(1) справедлив лишь в случае, когда существует хотя бы принципная возможность установить какое из вероятных событий вышло по сути (при освещении щелей Юнга коротковолновым излучением можно выяснить, по какому пути прошел электрон, законсложения (1) производится и интерференционной картины не возникает). Если же ситуация такая, что действия принципно неразличимы, суммарная возможность рассчитывается как квадрат модуля суммы всеохватывающих функций, именуемых амплитудами вероятностей:

(3) ,

при всем этом вероятности не суммируются, что, к примеру, и наблюдается в опытах по интерференции электронов (рис. 20_1). При движении в пустом пространстве амплитуда перехода частички из одной точки в другую совпадает с выражением для плоской монохроматической волны, частота которой связана с энергией формулой Планка . (Сравните формулу (3) с выражением, описывающим интерференцию света (19_8): далековато идущие выводы навязываются сами собой! Но, конкретно тут уместна большая осторожность: современная квантовая механика является нерелятивистской теорией и из ее законов конкретно не быть может получено исчерпающее описание ультрарелятивистской частички — фотона.)

3. В квантовой механике отвергается постулируемая в традиционном естествознании принципная возможность выполнения измерений и даже наблюдений объектов и происходящих с ними действий, не влияющих на эволюцию изучаемой системы. Это приводит к существованию пар канонически-сопряженных традиционных характеристик, одновременное сколь угодно четкое измерение которых оказывается неосуществимым (к ним относятся уже упоминавшиеся координата — импульс, время — энергия, и др.).

Законы традиционной физики получаются из квантовомеханических в пределе огромных масс составляющих систему тел. При всем этом, к примеру, даваемые соотношением неопределенности (1) ограничения на точность оказываются малосущественными:

(4) .

Выходящий из имеющей две открытые двери комнаты человек, в принципе, “будет интерферировать” подобно электрону в опыте Юнга, из-за что возникнут области в пространстве, где он не сумеет показаться. но из-за большенный массы человека размеры этих областей будут настолько малы (реально много меньше размеров наночастицы), что для настоящих задач макроскопического описания обозначенное явление заранее несущественно и даже не наблюдаемо. При рассмотрении же движения электрона (масса всего кг) в атоме (соответствующие размеры около м) соотношение неопределенности предвещает наличие заранее ненулевого импульса. Соответственная ему кинетическая энергия оказывается близкой по порядку величины к возможной энергии электростатического притяжения электрона к ядру. При всем этом соотношение неопределенности “не дает” электрону значительно приблизиться к ядру, так как при всем этом скорость его движения безизбежно обязана возрости. Т.о электрон в атоме является принципно квантово-механическим объектом. При квантово-механическом рассмотрении атома даже в рамках полу традиционной модели Резерфорда неувязка ультрафиолетовой катастрофы снимается.

“Древняя” и “новенькая” квантовые механики.

Основная награда в серьезной формулировке принципов квантовой механики принадлежит Н.Бору. В начальном варианте им использовалась планетарная модель атома Резерфорда, в рамках которой передвигающемуся по радиальный орбите электрону сопоставлялись волна, квадрат модуля которой определял возможность обнаружения электрона в данной точке (“волна ДеБройля”). Бор постулировал существование стационарных орбит, при движении по которым электрон не испускает электромагнитные волны (оказалось, что на таковых орбитах укладывается целое число длин волн ДеБройля). При переходе электрона с одной орбиты на другую изменение его энергии сопровождается излучением либо поглощением фотона. Таковая модель отлично разъясняла частотные закономерности в диапазоне излучения атомов водорода (19_5), но еще сохраняла черты отвергаемой традиционной теории (электроны в атоме имели линии движения, которые недозволено следить, не изменяя состояния атома). Теория не могла разъяснить неких деталей (“узкой структуры”), найденных при наиболее четких (интерферометрических) исследовательских работах диапазона водорода. Наиболее того, при помощи постулатов Бора не удавалось разъяснить наблюдаемые очень сложные диапазоны многоэлектронных атомов и их молекулярных соединений. В конце концов, “древняя” квантовая механика не разъясняла огромного количества остальных явлений, происходящих с атомами и молекулами, которые были уже отлично известны в химии.

Спустя наиболее, чем десятилетие, опосля сотворения первой квантово-механической модели атома водорода Н.Бором была построена новенькая законченная и непротиворечивая квантово-механическая теория, в целом с фуррором применяемая до реального времени. Как это уже не раз бывало в физике, ее создание потребовало развития новейшего математического аппарата, правильно описывающего сформулированные в ее рамках новейшие физические идеи.

Математический формализм квантовой механики: состояния, амплитуды, операторы. Существует несколько других математических формализмов, отвечающих главным физическим идеям квантовой механики. один из подходов состоит в рассмотрении состояний физической системы как векторов в пространстве, размерность которого определяется числом ее взаимоисключающих состояний, именуемых базовыми (на рис. 20_2 в качестве примера приведены два таковых состояния молекулы бензола с разными конфигурациями хим связей, допустимых традиционной теорией валентности). Под скалярным произведением 2-ух состояний понимается всеохватывающее число — амплитуда, квадрат модуля которой дает возможность отыскать систему в одном из перемножаемых состояний, если буквально понятно, что она находится в другом. В примере с молекулой бензола

,

где через обозначено состояние, соответственное “равномерному распределению хим связей” , к признанию настоящего существования которого химия шла довольно долгим методом.

Для описания измеряемых физических величин F в квантовой механике вводятся операторы , деяния которых на векторы состояний в общем случае приводят к возникновению новейших векторов:

(6)

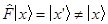
(так на языку арифметики описывается тот факт, что процедура измерения оказывает воздействие на изучаемую квантово-механическую систему). Наблюдаемое на опыте среднее

.

Т.о. математический аппарат современной квантовой механики нацелен на вычисления вероятностей пребывания физических систем в тех либо других состояниях и средних значений физических величин, характеризующих эту систему, т.е. как раз те величины, которые могут быть измерены в настоящем опыте.

Эволюция во времени квантово-механических систем. Для описания конфигурации системы во времени вводится оператор эволюции, связывающий ее состояния в два близких момента:

.

Если оператор эволюции известен, его последовательное применение к начальному состоянии системы дозволяет проследить за ее временным развитием, т.е. решить основную задачку естествознания. Обычно оператор эволюции за нескончаемо малый просвет времени записывают в виде

,

где — оператор Гамильтона. Подстановка выражения (9) в (8) приводит к основному уравнению квантовой механики

,

играющему настолько же важную роль в квантовой теории, как законы Ньютона в традиционном естествознании. По собственному смыслу оператор Гамильтона является обобщением традиционного понятия энергии, так как для личного варианта стационарной изолированной системы (где энергия сохраняется) уравнение (10) имеет решение

,

совпадающее с волной ДеБройля и удовлетворяющее стационарному уравнению

.

Стационарные состояния квантово-механических систем.

При решении уравнения (11) определяются стационарные состояния системы и надлежащие им значения энергии W. В случае дискретного набора разрешенных энергий молвят о энергетических уровнях системы, в случае непрерывного набора — о непрерывном диапазоне энергий. к примеру, базовые состояния и молекулы бензола не являются стационарными: являющаяся следствием соотношения неопределенности неточная локализация электронов в пространстве приводит к способности перехода этих состояний друг в друга (т.н. туннельный эффект). Уравнение (12) дозволяет найти два сохраняющихся во времени состояния, которые оказываются симметричной и антисимметричной линейными комбинациями базовых:

,

и найти надлежащие им энергии

.

Т.о. наличие способности переходов меж 2-мя эквивалентными состояниями приводит к появлению в системе 2-ух энергетических уровней заместо 1-го (рис. 20_3). Система может находиться только в одном из построенных стационарных состояний ( ), но в любом из их возможность отыскать традиционно осмысленную конфигурацию либо схожа и равна 0.5. Симметричное стационарное состояние энергетически наиболее прибыльно и более нередко реализуется в природе.

Аммиачный мазер. Существует огромное количество различных систем, владеющих 2-мя базовыми состояниями, не сохраняющимися во времени. К ним относится молекула аммиака, с традиционной точки зрения имеющая две конфигурации либо , способные преобразовываться друг в друга из-за туннельного эффекта (рис. 20_4). Стационарные энерго уровня молекулы разбиты зазором, энергетически соответственном высокочастотному радиоизлучению. Настроенное в резонанс наружное электромагнитное поле способно вызывать переходы меж этими состояниями, которых сопровождаются поглощением либо излучением энергии в виде электромагнитных волн (на другом языке — фотонов). Ансамбль из молекул, находящихся в верхнем энергетическом состоянии способен лишь источать энергию, т.е. вести взаимодействие с электромагнитным полем, усиливая его. На описанном принципе базирована работа первого мазера — лазера, работающего в радио спектре излучения.

Природа хим связи. Системой с 2-мя состояниями является простейшее хим соединение — молекулярный ион водорода (рис. 20_5). Как и в рассмотренных выше вариантах предпосылкой не сохранения во времени избранных базовых состояний является туннельный эффект. При сближении ядер возможность туннельного перехода электрона от 1-го к другому увеличивается , что приводит к повышению расстояния меж подуровнями и делает симметричное состояние иона энергетически наиболее прибыльным. “Стремясь к понижению полной энергии”, ядра сближаются, что воспринимается как итог деяния доборной силы, обеспечивающей появление хим связи.

Природа электростатических и ядерных взаимодействий. В общих чертах схожий механизм лежит в базе современных представлений о появлении электростатических взаимодействий меж электронными зарядами. Заместо “туннелирующего” электрона в молекулярном ионе роль переносчика электронных взаимодействий меж зарядами играют виртуальные фотоны, обнаружения которых в настоящем опыте оказывается принципно неосуществимым.

Схожий механизм был предложен и в случае мощных ядерных взаимодействий. Резвый спад ядерных сил при увеличении расстояний привел к допущению, что переносчиком взаимодействия является на владеющий нулевой массой покоя фотон, а очень томная частичка с массой, превосходящей электрическую приблизительно в 200 раз. Скоро такие частички были обнаружены в галлактических лучах (пи-мезоны), но последующие опыты проявили их непричастность к ядерным силам. Но выдвинутая догадка все таки оказалась жизнестойкой: потом были обнаружены похожие на ранее открытые мезоны частички, характеристики которых согласовывались с предсказанными на базе анализа ядерных сил.

Электропроводность кристаллов. Системы с 2-мя состояниями владеют 2-мя энергетическими подуровнями . Повышение числа эквивалентных состояний приводит к возникновению большего числа подуровней. Примером системы с огромным числом состояний может служить электрон в безупречном кристалле, который быть может локализован поблизости всякого из N часто расположенных ионов, что соответствует набору базовых состояний: (рис. 20_6). Самой низкой энергии соответствует симметричная линейная композиция базовых состояний:

,

остальные ортогональные линейные композиции дают систему из близлежащих друг к другу N энергетических подуровней. При увеличении числа атомов в кристалле подуровни соединяются в сплошную полосу — энергетическую зону, подобающую непрерывному набору разрешенных значений энергии электрона. Так как вольная частичка в пустом пространстве так же может владеть энергией из непрерывного набора, , для всякого из которых быть может записано уравнение, аналогичное (10). Определенный вид оператора Гамильтона для этого варианта был верно угадан Шредингером и имеет вид, аналогичный традиционному выражению для механической энергии:

,

где — оператор импульса, — оператор возможной энергии. Больший практический Энтузиазм представляют вероятности найти находящуюся в стационарном состоянии частичку в данной точке места R. В согласовании с общими правилами квантовой механики эта возможность дается квадратом модуля соответственной амплитуды, именуемой волновой функцией:

.

анализ математических параметров стационарного уравнения Шредингера

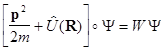
указывает, что в вариантах, когда область традиционно вероятного движения частички в пространстве ограничена, разрешенным является лишь дискретный набор энергетических уровней. При неограниченном движении энергетический диапазон непрерывен.

В простом случае стационарных решений для атома водорода связанным состояниям (электрон находится поблизости ядра) соответствует набор разрешенных значений энергии, на сто процентов совпадающий с вычисленными в рамках первой модели Бора и отлично согласующийся с тестом (рис. 20_7). В ионизованном состоянии (электрон ушел от ядра на нескончаемо огромное расстояние) частичка может владеть хоть каким значением энергии.

]]>