Учебная работа. Реферат: Синтез адаптивной системы автоматического управления

Учебная работа. Реферат: Синтез адаптивной системы автоматического управления

часть
I
. Синтез управляющих устройств

Начальные данные

На рисунке приведена структурная схема поочередного соединения исполнительного механизма и объекта управления.

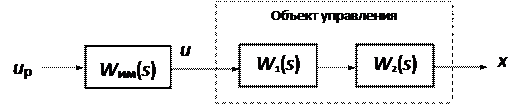
В качестве исполнительного механизма употребляется механизм неизменной скорости с ограничением:

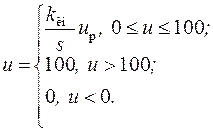
объект управления описывается передаточными функциями вида:

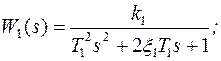
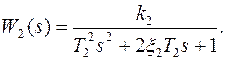
Численные значения характеристик исполнительного механизма и объекта управления:

Вариант
kим

k1

k2

T1

T2

x1

x2


11
0,20
1,00
1,00
1,80
3,80
0,80
0,80

Задание:

Провести анализ динамических параметров объекта управления с внедрением графиков переходного процесса и АЧХ. При определении продолжительности переходного процесса принять D = ±5% от установившегося значения выходной переменной.

Для моделирования системы управления используем программку МВТУ (моделирование в технических устройствах).

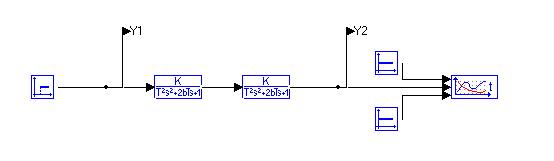
Рис.1 – объект управления

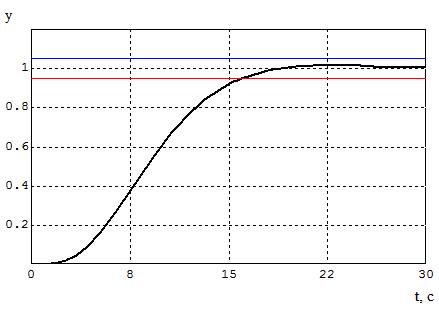
Рис.2 – График переходного процесса

По графику видно, что система является устойчивой с плавным переходным действием без перерегулирования. Установившееся

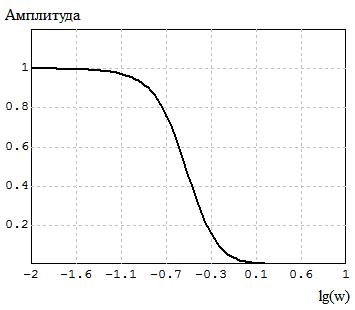
Рис.3 – График АЧХ

АЧХ указывает, во сколько раз амплитуда сигнала на выходе системы различается от амплитуды входного сигнала на всём спектре.

max


= A0
= 1;

: A = 0.01

c


= 0,0551;

: A = 0.707 ωп


= 0,6316.

2 РАЗРАБОТКА ЛИНЕЙНОГО РЕГУЛЯТОРА

характеристики ступенчатого входного действия:

1) время «включения» скачка t = 0;

2)

3)

На рисунке 2.1 изображена схема поочередно соединённых исполнительного механизма и объекта управления, на которые подаётся ступенчатое входное действие.

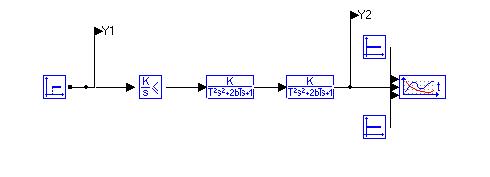
Набросок 2.1 — Схема поочередно соединённых исполнительного механизма и объекта управления.

График переходного процесса, протекающего в системе управления, изображён на рисунке 2.2.

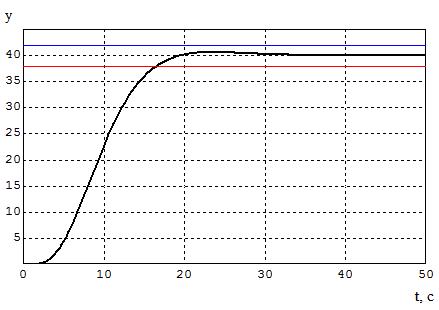
Набросок 2.2 – Переходной процесс

В данной схеме 2.1 исполнительный механизм представляет собой интегратор с ограничениями. Потому при выбирании регулятора нужно учесть, что интегральная составляющая в схеме уже находится.

Существует два вида регуляторов без интегральной составляющей: П-регулятор и ПД-регулятор. Добавка П-регулятора в систему управления делает её высокоточной в установившемся режиме, но в переходном режиме свойство системы усугубляется. Передаточная функция П-регулятора:

.

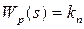Её соединение с передаточной функцией исполнительного механизма даст:

.

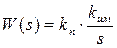соединение пропорциональной и интегральной составляющих прирастит точность системы управления.

ПД-регулятор улучшает свойство системы в переходном режиме, на свойство системы в установившемся режиме влияет слабо. Передаточная функция ПД-регулятора:

.

Её соединение с передаточной функцией исполнительного механизма даст:

.

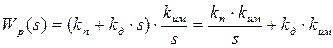соединение пропорциональной и интегральной составляющих прирастит точность системы управления, а соединение дифференциальной и интегральной составляющих прирастит быстродействие системы.

Нужно получить резвый переходной процесс без перерегулирования, как следует, более пригодным для этого является ПД-регулятор. Схема линейного регулятора в системе управления изображена на рисунке 2.3.

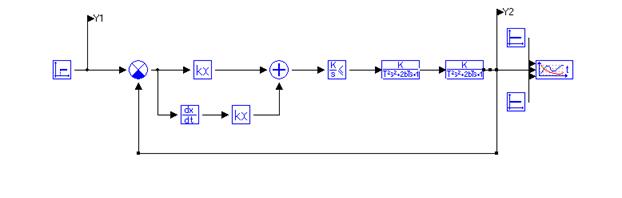
Набросок 2.3 – Схема с линейным регулятором

3 РАСЧЕТ ПАРАМЕТРОВ РЕГУЛЯТОРА

Для определения численных значений характеристик линейного регулятора воспользуемся способом Циглера –Никольса.

Регулятор управляет объектом с таковой передаточной функцией:

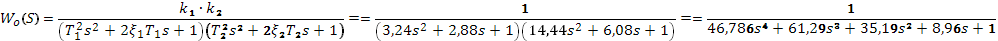
Передаточная функция разомкнутой системы:

Дальше используем аспект Найквиста:

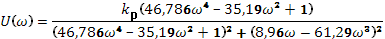
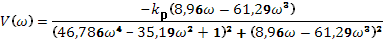
Нужно довести систему до границы стойкости

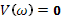
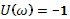
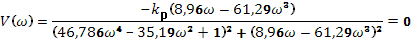
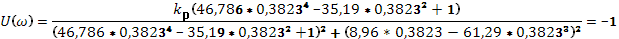
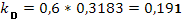
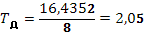
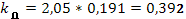
Исходя из передаточной функции ПД-регулятора для данного проектирования, Wр
(S)=kp
(1+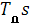), характеристики регулятора

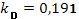
При отысканных параметрах получаем переходной процесс без перерегулирования, изображенный на рис. 3.2. время переходного процесса – 62с.

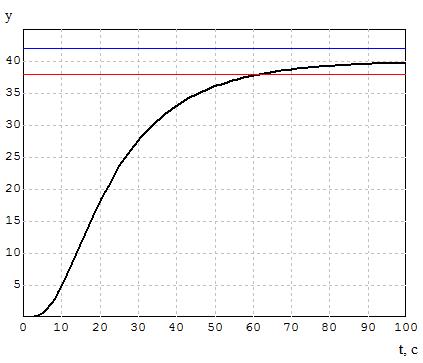
Набросок 3.2 – График переходного процесса при избранных параметрах базисного регулятора.

4 анализ ДИНАМИЧЕСКИХ СВОЙСТВ САУ

Проведём анализ динамических параметров САУ, синтезированной в первой части расчетной работы, при
2
= 0,4. График переходного процесса изображен на рисунке 4.1.

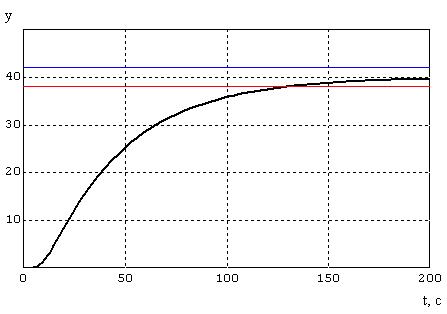
Набросок 4.1 – График переходного процесса

процесс проходит плавненько, без перерегулирования, время переходного процесса t = 129 c.

Проведём анализ динамических параметров САУ, синтезированной в первой части расчетной работы, при
2
= 1,6. График переходного процесса изображен на рисунке 4.2.

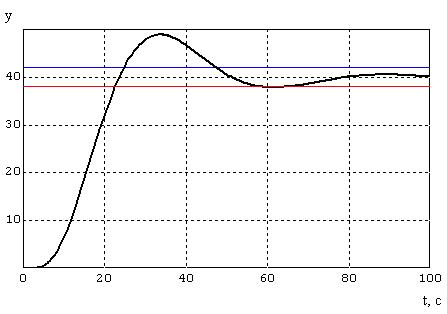
Набросок 4.2 – График переходного процесса

процесс колебательный, с перерегулированием. Время переходного процесса t = 23 c.

Перерегулирование σ = 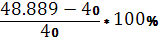= 22,2225%.

Проведем анализ САУ при случайном изменении коэффициента усиления
1
(при
2
= 1,0) в виде обычного шума с математическим ожиданием, равным
k
= 1,0, и дисперсией, равной
k
= 0,2. Схема модели представлена на рисунке 4.3.

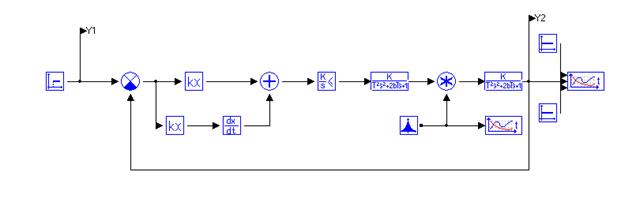
Набросок 4.3 – Схема модели с внедрением блока «Обычный шум»

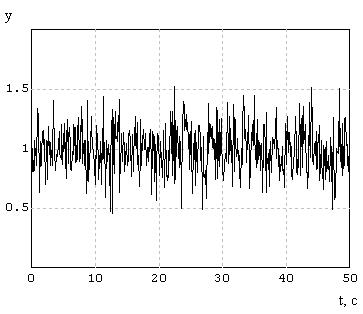
Набросок 4.4 – График обычного шума

График переходного процесса изображен на рисунке 4.4. время переходного процесса t = 35 c.

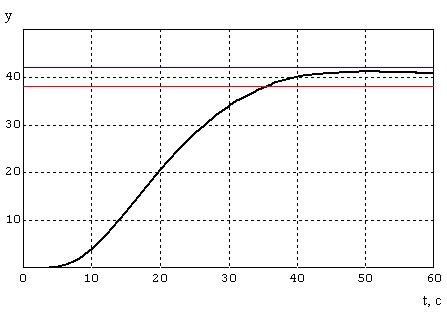
Набросок 4.4 – График переходного процесса.

5 ФОРМИРОВАНИЕ ЭТАЛОННОЙ МОДЕЛИ САУ

В качестве эталонной модели возьмем апериодическое звено 2-го порядка с передаточной функцией

.

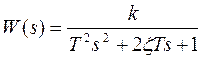k=1 – увеличивает либо уменьшает сигнал;

T=5.5 – влияет на скорость переходного процесса;

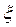=0.75.

Схема с эталонной моделью представлена на рисунке 5.1. На рисунке 5.2 изображены переходные процессы моделей. время переходного процесса эталонной модели t = 20.2c.

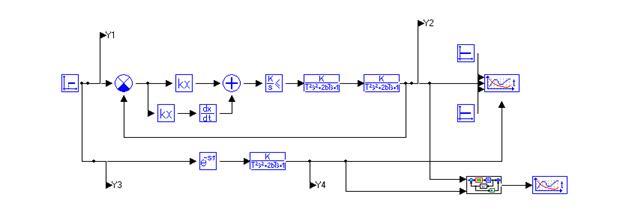
Набросок 5.1 – Схема эталонной и настоящей моделей.

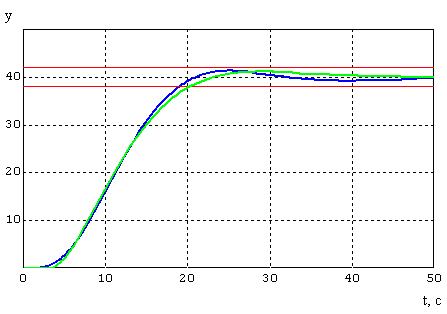
Набросок 5.2 – Графики переходных действий моделей.

6 СРАВНИТЕЛЬНЫЙ анализ ЭТАЛОННОЙ МОДЕЛИ И РЕАЛЬНОЙ САУ

Среднеквадратическая ошибка рассчитывается по формуле:

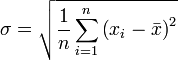
Для вычисления СКО в структуру модели добавлен микроблок, реализующий данную формулу:

Описание микроблока: в блок поступают 2 сигнала – с настоящей и эталонной моделей, потом берется их разность и модуль числа, чтоб не было отрицательных значений. Потом, согласно формуле заданы возведение в квадрат и квадратный корень. Блок «Ключ интегратора» описывает количество точек.

Набросок 6.1 – Структура блока СКО.

На выходе блока стоит график, показывающий k2

= 1.

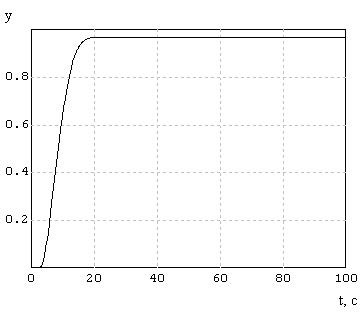
Набросок 6.2 – k
2

= 1.

При
2
= 0,4 вид переходного процесса настоящей модели показан на рисунках 6.3. СКО составляет σ = 3,6237 (набросок 6.4).

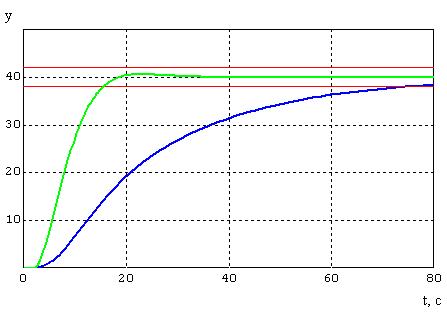
Набросок 6.3 – График переходного процесса при
2
= 0,4.

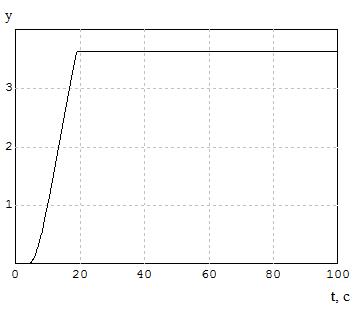
Набросок 6.4 – График СКО настоящей модели при
2
= 0,4.

При
2
= 1,6 переходной процесс имеет последующий вид (набросок 6.5). СКО составляет σ = 3,052 (набросок 6.6).

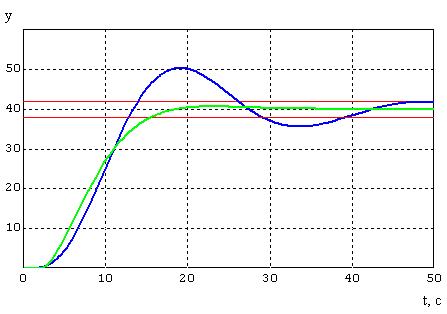
Набросок 6.5 — График переходного процесса при
2
= 1,6.

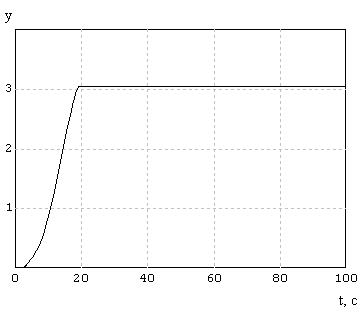
Набросок 6.6 – График СКО настоящей модели при
2
= 1,6.

7 синтез АДАПТИВНОЙ САУ С ЭТАЛОННОЙ МОДЕЛЬЮ

Главный задачей адаптивного контура является поддержание сигнала на данной уровне при параметрическом возмущении. Было установлено, что при изменении в объекте
2

меняется и переходной процесс.

При
2

= 0,4 переходной процесс протекает довольно длительно, как следует в адаптивном контуре мы должны уменьшить его время.

При
2

= 1,6 в переходном процессе возникает колебания, как следует нужно их погасить.

Добавим в модель график (набросок 7.1) и поглядим k
2

в объекте.

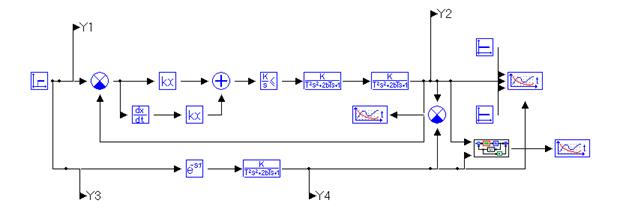
Набросок 7.1 – Схема модели.

Поменяем k
2

на 0,4, а потом на 1,6 и проанализируем изменение различия 2-х сигналов. На рисунке 7.2 лицезреем, что разница сигналов при
2

= 0,4 воспринимает отрицательные значения, а при
2

= 1,6 (набросок 7.3) значения различия положительные и отрицательные. Как следует при построении адаптивного контура нужно учесть значения различия 2-х сигналов и соответственно реагировать на её изменении. В адаптивном контуре будет две параллельных ветки, которые при изменении знака различия 2-х сигналов будут реагировать на изменение
2

в объекте. Для переключения меж ветвями используем ключ 2А.

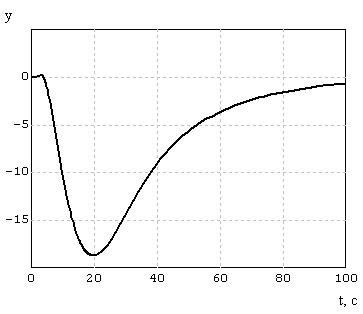
Набросок 7.2 – k
2

= 0,4.

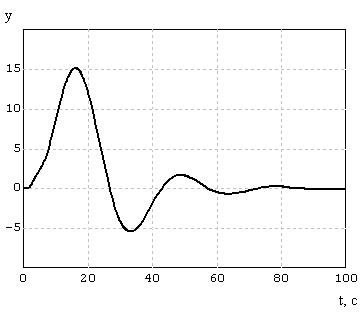
Набросок 7.3 – k
2

= 1,6.

Для ветки, реагирующей на
2

= 0.4 построим последующую структуру. Когда значения сигнала. Потом усилителем увеличиваем разницу сигналов, чтоб переходной процесс ОУ совпадал с эталонной моделью. Опосля прохождения данной для нас ветки сигнал должен быть отрицательным.

Для ветки, реагирующей на
2

= 1.6, структуру постоем по другому. Когда k
2

= 1.6 в системе возникают колебания, то при помощи производной уменьшаем их. Потом апериодическим звеном первого порядка сглаживаем оставшиеся колебания и уменьшаем время. Опосля прохождения апериодического звена первого порядка сигнал воспринимает отрицательные и положительные значения. Нужно на выходе из 2-ой ветки получить лишь положительные значения сигнала, потому излом пропустит лишь положительный сигнал.

Схема адаптивного контура представлена на рисунке 7.4.

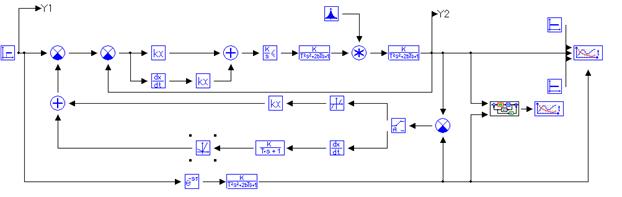
Набросок 7.4 – Схема адаптивного контура.

характеристики применяемых блоков:

1) усилитель с зоной нечувствительности: a = -3.1, b = 3.1, k = 1;

2) усилительkx: k=8;

3) апериодическое звено I порядка:k = 5, T = 0.001;

4) излом: k1
= 0, k2
= 1.8.

Графики переходных действий при
2

= 1,
2

= 0,4 и
2

= 1,6 изображены на рисунках 7.5, 7.7 и 7.9 соответственно. При
2

= 1 СКО равно 0.114, при
2

= 0,4 СКО равно 2.63, при
2

= 1.6 СКО равно 2.2.

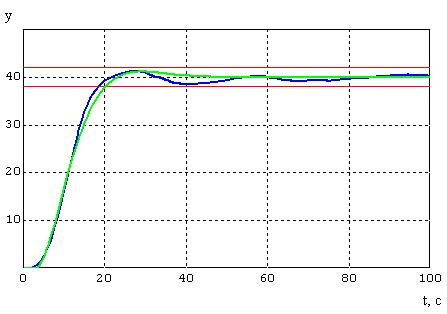
Набросок 7.5 — График переходного процесса при
2

= 1.

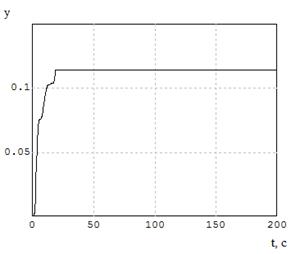
Набросок 7.6 – график СКО при
2

= 1.

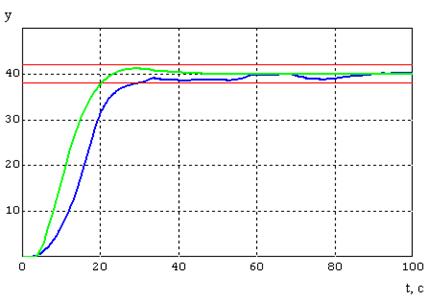
Набросок 7.7 — График переходного процесса при
2

= 0,4.

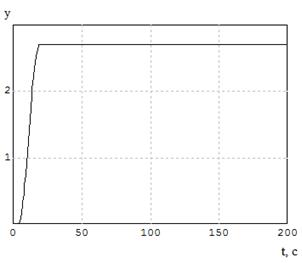
Набросок 7.8 – график СКО при
2

= 0,4.

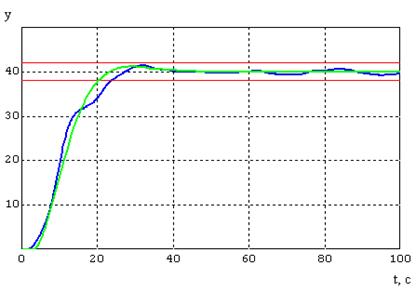
Набросок 7.9 — График переходного процесса при
2

= 1,6.

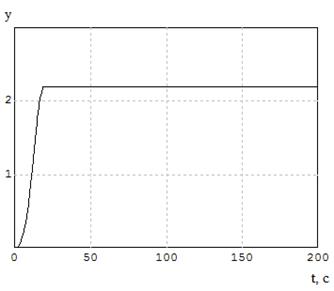
Набросок 7.10 – график СКО при
2

= 1,6.

Вывод:

В первой части расчетной работы я провел анализ динамических параметров данного объекта управления и сконструировал линейный регулятор, обеспечивающий перевод объекта из исходного состояния в конечное. Также способом незатухающих колебаний Циглера-Никольса были рассчитаны характеристики линейного регулятора.

В процессе выполнения 2-ой части работы — «Синтез адаптивной САУ с эталонной моделью», был проведен анализ динамических параметров САУ, синтезированной в первой части работы. Был проведен сравнительный анализ настоящей и эталонной модели, при использовании разных коэффициентов и проверка среднеквадратической ошибки. Также выбрана эталонная модель.

В итоге была сформирована адаптивная САУ, которая поддерживает уровень сигнала на данном уровне, при этом в адаптивной системе среднеквадратическое отклонение миниатюризируется практически вдвое, соответственно и погрешность уменьшилась.

]]>