Учебная работа. Реферат: Влияние вращательного и поступательного движения молекул на теплоёмкость многоатомных газов

Учебная работа. Реферат: Влияние вращательного и поступательного движения молекул на теплоёмкость многоатомных газов

Вступление

До этого чем приступить к подробному вычислению термодинамических величин газов с учетом разных квантовых эффектов, полезно разглядеть эту же задачку исходя из убеждений чисто традиционной статистики. В предстоящем мы увидим, в которых вариантах и в которой мере получающиеся при всем этом результаты могут быть использованы к настоящим газам.

Молекула представляет собой конфигурацию атомов, совершающих малые колебания около определенных положении равновесия, соответственных минимуму возможной энергии их взаимодействия. Крайняя имеет при всем этом вид

,

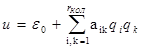где e0
— возможная энергия взаимодействия атомов, когда они все находятся в положениях равновесия; 2-ой же член есть квадратичная функция координат, определяющих отличия атомов от положений равновесия. Число rкол
координат в данной нам функции есть число колебательных степеней свободы молекулы. Крайнее можно найти по числу п атомов в молекуле. Конкретно, n-атомная молекула имеет всего 3п степеней свободы. Из их три соответствуют поступательному движению молекулы как целого и три — ее вращению как целого. Если все атомы размещены по одной прямой (в .частности, у двухатомной молекулы), то вращательных степеней свободы всего две. Таковым образом, нелинейная n-атомная молекула имеет всего 3п — 6 колебательных степеней свободы, а линейная 3п — 5. При п = 1 колебательных степеней свободы, естественно, совершенно нет, потому что все три степени свободы атома соответствуют поступательному движению.

Полная энергия e молекулы есть сумма возможной и кинетической энергий. Крайняя является квадратичной функцией от всех импульсов, число которых равно полному числу 3п степеней свободы молекулы. Потому энергия e имеет вид

,

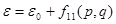где f11
(p,q) — квадратичная функция импульсов и координат; полное число переменных в данной нам функции есть l = 6n—6 (для нелинейной молекулы) либо l = 6n—5 (для линейной); у одноатомного газа l = 3, потому что координаты совершенно не входят в выражение для энергии.

Подставляя это выражение для энергии в формулу

где интегрирование делается по фазовому месту молекулы, а ,

имеем

.

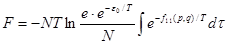Для того чтоб найти температурную зависимость входящего сюда интеграла, произведем подстановку 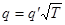для всех l переменных, от которых зависит функция f11
(р, q). Вследствие квадратичности данной нам функции будет:

,

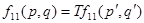и T в показателе подынтегрального выражения сократится. Преобразование же дифференциалов этих переменных, входящих в dt, даст множитель Tl
/2
, который выносится за символ интеграла. Интегрирование по колебательным координатам q делается по той области их значений, которая соответствует колебаниям атомов снутри молекулы. Так как, но, подынтегральная функция стремительно миниатюризируется с повышением q, то интегрирование можно распространить на всю область от -¥ до +¥, как и для всех импульсов. Изготовленная нами подмена переменных не изменит тогда пределов интегрирования, и весь интеграл будет некой не зависящей от температуры неизменной. Беря во внимание также, что интегрирование по координатам центра инерции молекулы дает занимаемый газом размер V, получим в итоге для вольной энергии выражение вида

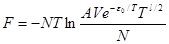, (1.1)

где (А — неизменная).

Мы увидим в предстоящем, что в целом ряде принципиальных случаев теплоемкость газа оказывается – в наиболее либо наименее значимых интервалах температуры – величиной неизменной, не зависящих от температуры. Имея в виду это событие, мы вычисляем тут в общем виде термодинамические величины такового газа.

Дифференцируя выражение

для энергии, найдем, что функция f(T) связана с теплоемкостью сu
средством – Тf’’(T)=cu
. Интегрируя это соотношение, получим:

где z и e0
– неизменные. Подставляя это выражение в

получим для вольной энергии последующее окончательное выражение:

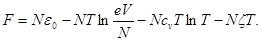(1.2)

где z — хим неизменная газа.

Раскрывая логарифм в выражении (1.1), мы получим в точности выражение типа (1.2) с неизменной теплоемкостью, равной

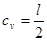(1.3)

Таковым образом, чисто традиционный безупречный газ должен владеть неизменной теплоемкостью. Формула (1.3) дозволяет при всем этом высказать последующее правило: на каждую переменную в энергии e(р, q) молекулы приходится по равной доле 1/2 в теплоемкости cv
газа (k/2 в обыденных единицах), либо, что то же, по равной доле Т/2 в его энергии. Это правило именуют законом равнораспределения.

Имея в виду, что от поступательных и вращательных степеней свободы в энергию e(р, q) входят лишь надлежащие им импульсы, мы можем сказать, что любая из этих степеней свободы заносит в теплоемкость вклад, равный 1/2. От каждой же колебательной степени свободы в энергию e(р, q) заходит по две переменных (координата и импульс), и ее вклад в теплоемкость равен 1.

Вращательная теплоемкость многоатомных газов.

Вольную энергию многоатомного газа, как и двухатомного, можно представить в виде суммы 3-х частей — поступательной, вращательной и колебательной. Поступательная часть характеризуется теплоемкостью и хим неизменной, равными:

Благодаря большенный величине моментов инерции многоатомных молекул (и соответственно малости их вращательных квантов) их вращение можно постоянно разглядывать традиционно[1]
. Многоатомная молекула владеет 3-мя вращательными степенями свободы и 3-мя в общем случае разными главными моментами инерции I1
, I2
, I3
; потому ее кинетическая энергия вращения есть

где, — координаты вращающейся системы, оси которой совпадают с главными осями инерции молекулы, (оставляем пока в стороне особенный вариант молекул, составленных из атомов, расположенных на одной прямой). Это выражение обязано быть подставлено в статистический интеграл

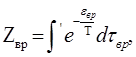(2.1)

где

а штришок у интеграла значит, что интегрирование обязано выполняться только по тем ориентациям молекулы, которые на физическом уровне отличны друг от друга.

Если молекула владеет какими-либо осями симметрии, то повороты вокруг этих осей совмещают молекулу саму с собой и сводятся к перестановке схожих атомов. ясно, что число на физическом уровне неразличимых ориентации молекулы равно числу допускаемых ею разных поворотов вокруг осей симметрии (включая тождественное преобразование—поворот на 360°). Обозначив это число средством [2]
, можно создавать интегрирование в (2.1) просто по всем ориентациям, сразу разделив все выражение на  В произведении dx
dh
dz
3-х нескончаемо малых углов поворота) можно разглядывать dx
, dh
 как элемент dsz
телесного угла для направлений оси z.

Интегрирование по dsz
делается независимо от интегрирования по поворотам dz
вокруг самой оси z и дает 4p. Опосля этого интегрирование по djz
 дает еще 2p.

Интегрируя также и по dMx
dMh
dMz
(в границах от -¥ до +¥), найдем в итоге

Отсюда вольная энергия

Таковым образом, для вращательной теплоемкости имеем в согласовании с (1.3)

а хим неизменная

Если все атомы в молекуле размещены на одной прямой (линейная молекула), то она владеет, как и двухатомная молекула, всего 2-мя вращательными степенями свободы и одним моментом инерции /. Вращательные теплоемкость и хим неизменная равны, как и у двухатомного газа,

где s=1 для несимметричной молекулы (к примеру, NNO) и s=2 для молекулы, симметричной относительно собственной середины (к примеру, ОСО).

Колебания молекул.

Колебательная часть термодинамических величин газа становится значимой при существенно наиболее больших температурах, чем вращательная, поэтому что интервалы колебательной структуры термов значительны по сопоставлению с интервалами вращательной структуры.

Мы будем считать, но, температуру большенный только так, чтоб были возбуждены в главном не очень высочайшие колебательные уровни. Тогда колебания являются малыми (а поэтому и гармоническими), и уровни энергии определяются обыденным выражением ħw(u + 1
/2
).

Число колебательных степеней свободы описывает число так именуемых обычных колебаний молекулы, любому из которых соответствует своя частота wa
(индекс a нумерует обычные колебания). нужно подразумевать, что некие из частот wa
могут совпадать друг с другом; в таковых вариантах молвят о кратной частоте.

Вычисление колебательной статистической суммы Zкол
делается тривиально. Вследствие весьма резвой сходимости ряда суммирование можно формально распространить до u=¥. Условимся отсчитывать энергию молекулы от более низкого (u = 0) осциллирующего уровня, т. е. включаем ħw/2 в постоянную e0
в

В гармоническом приближении, когда мы считаем колебания малыми все обычные колебания независимы, и колебательная энергия есть сумма энергий всякого колебания в отдельности. Потому колебательная статистическая сумма

,

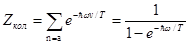распадается на произведение статистических сумм отдельных колебаний,

а для вольной энергии FKOJl
выходит сумма выражений

,

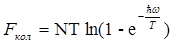т. е.

В эту сумму любая частота заходит в числе раз, равном ее кратности. Такового же рода суммы получаются соответственно для колебательных частей остальных термодинамических величин.

Каждое из обычных колебаний дает в собственном традиционном предельном случае (T>>ħwa
) вклад в теплоемкость, равный c(
a
)
кол
= 1 при Т, большем большего из ħwa
, вышло бы скол
= rкол
. Практически, но, этот предел не достигается, потому что многоатомные молекулы обычно распадаются при существенно наиболее низких температурах.

Разные частоты wa
многоатомной молекулы разбросаны обычно в весьма широком интервале значений. По мере увеличения температуры равномерно «врубаются» в теплоемкость разные обычные колебания. Это событие приводит к тому, что теплоемкость многоатомных газов в достаточно широких интервалах температуры нередко можно считать приблизительно неизменной.

Упомянем о способности типичного перехода колебаний во вращение, пример которого представляет молекула этана С2
Н6
. Эта молекула построена из 2-ух групп СН3
, находящихся на определенном расстоянии друг от друга и определенным образом взаимно нацеленных. Одно из обычных колебаний молекулы представляет собой «крутильное качание», при котором одна из групп СН3
поворачивается относительно иной. При увеличении энергии колебаний их амплитуда вырастает и в конце концов, при довольно больших температурах, колебания перебегают в свободное вращение. В итоге вклад данной нам степени свободы в теплоемкость, достигающий при полном возбуждении колебаний приблизительно величины 1, при предстоящем повышении температуры начинает падать, асимптотически приближаясь к соответствующему для вращения значению 1/2.

В конце концов, укажем, что если молекула владеет хорошим от нуля спином S (к примеру, молекулы NO2
, C1O2
), то к хим неизменной добавляется величина

Заключение

До сего времени мы разглядывали вращение и колебания как независящие движения молекулы, в реальности же одновременное наличие того и другого приводит к типичному взаимодействию меж ними (Е, Teller, L. Tisza, G. Placzek, 1932— 1933).

Начнем с рассмотрения линейных многоатомных молекул. Линейная молекула может совершать колебания 2-ух типов — продольные с ординарными частотами и поперечные с двукратными частотами. Нас будут заинтересовывать на данный момент крайние.

Молекула, совершающая поперечные колебания, владеет, совершенно говоря, неким моментом импульса. Это разумеется уже из обычных механических суждений[3]
, но быть может показано и квантовомеханическим рассмотрением. Крайнее дозволяет также найти и вероятные значения этого момента в данном колебательном состоянии.

Представим, что в молекуле возбуждена какая-либо одна двукратная частота wа
. Уровень энергии с колебательным квантовым числом va
вырожден (va
+ 1)-кратно. Ему соответствует va
+ 1 волновых функций

(где va
1
+ va
2
= va
) либо какие-либо любые их независящие линейные композиции. Общая (по Qa
l
и Qa
2
) старшая степень полинома, на который множится экспоненциальный множитель, во всех этих функциях схожа и равна va
. Разумеется, что постоянно можно избрать в качестве главных функций линейные композиции функций 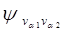вида

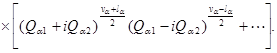(3.1)

В квадратных скобках стоит определенный полином, из которого мы выписали лишь старший член. la
есть целое число, способное принимать va
+ 1 разных значений:

la
= va
, va
— 2, va
— 4, …, — va
.

Обычные координаты Qa
1
, Qa
2
поперечного колебания представляют собой два взаимно перпендикулярных смещения от оси молекулы. При повороте вокруг данной нам оси на угол

j старший член полинома (а с ним и вся функция 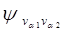) умножится на

Отсюда видно, что функция (3,1) соответствует состоянию с моментом 1a
относительно оси.

Таковым образом, мы приходим к результату, что в состоянии, в каком возбуждена (с квантовым числом va
) двукратная частота wa
, молекула владеет моментом (относительно собственной оси), пробегающим значения

О нем молвят, как о колебательном моменте молекулы. Если возбуждено сразу несколько поперечных колебаний, то полный колебательный момент равен сумме åla
. Сложенный с электрическим орбитальным моментом, он дает полный момент l молекулы относительно ее оси.

Полный момент импульса молекулы J не быть может меньше момента относительно оси, т. е. J пробегает значения

Иными словами, состояний с J =0, 1, …. | l | — 1 не существует.

При гармонических колебаниях энергия зависит лишь от чисел va
и не зависит от la
. Вырождение колебательных уровней (по значениям la
) снимается при наличии ангармоничности. Снятие, но, неполное: уровни остаются дважды вырожденными, при этом схожей энергией владеют состояния, отличающиеся одновременным конфигурацией знака всех la
и l; в последующем (опосля гармонического) приближении в энергии возникает квадратичный по моментам la
член вида

(ga
b
— неизменные). Это остающееся двукратное вырождение снимается эффектом, аналогичным L-удвоению у двухатомных молекул.

Переходя к нелинейным молекулам, нужно до этого всего создать последующее замечание чисто механического нрава. Для случайной (нелинейной) системы частиц возникает вопросец о том, каким образом можно совершенно отделить осциллирующее движение от вращения, иными словами, что следует осознавать под «невращающейся системой». На 1-ый взор, можно было бы пошевелить мозгами, что аспектом отсутствия вращения может являться равенство нулю момента импульса:

(суммирование по частичкам системы). Но стоящее слева выражение не является полной производной по времени какой-нибудь функции координат. Потому написанное равенство не быть может проинтегрировано по времени так, чтоб быть сформулированным в виде равенства нулю некой функции координат. Меж тем конкретно это нужно для того, чтоб можно было разумным образом сконструировать понятие о «незапятнанных колебаниях» и «чистом вращении».

Потому в качестве определения отсутствия вращения нужно взять условие

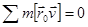, (3.2)

где r0
— радиусы-векторы положений равновесия частиц. Написав r = r0
+ u, где u — смещения при малых колебаниях, имеем v = r = u. Уравнение (3.2) встраивается по времени, в итоге что получаем

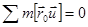, (3.3)

Движение молекулы мы будем разглядывать как совокупа чисто осциллирующего движения, при котором удовлетворяется условие (3.3), и вращения молекулы как целого[4]
. Написав момент импульса в виде

,

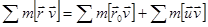мы лицезреем, что, в согласовании с определением (3.2) отсутствия вращения, под колебательным моментом нужно осознавать сумму . Нужно, но, подразумевать, что этот момент, являясь только частью полного момента системы, сам по для себя никак не сохраняется. Потому любому колебательному состоянию можно приписать только среднее

Молекулы, не владеющие ни одной осью симметрии наиболее чем второго порядка, относятся к типу асимметричного волчка. У молекул этого типа все частоты колебаний — обыкновенные (их группы симметрии владеют лишь одномерными неприводимыми представлениями). Потому все колебательные уровни не вырождены. Но во всяком невырожденном состоянии средний момент импульса обращается в нуль. Таковым образом, у молекул типа асимметричного волчка средний колебательный момент во всех состояниях отсутствует.

Если в числе частей симметрии молекулы имеется одна ось наиболее чем второго порядка, молекула относится к типу симметричного волчка. Таковая молекула владеет колебаниями как с ординарными, так и с двукратными частотами. Средний колебательный момент первых опять обращается в нуль. Двухкратным же частотам, соответствует хорошее от нуля среднее

Просто отыскать выражение для энергии вращательного движения молекулы (типа симметричного волчка) с учетом осциллирующего момента.

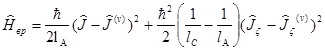. (3.4)

Разыскиваемая энергия есть среднее тут эффект взаимодействия колебаний молекулы с ее вращением; его именуют кориолисовым взаимодействием (имея в виду его соответствие кориолисовым силам в традиционной механике).

При усреднении этих членов нужно подразумевать, что средние значения поперечных (x, h) компонент осциллирующего момента равны нулю. Потому для среднего значения энергии кориолисового взаимодействия получаем:

,

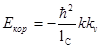где k (целое число) есть, — среднее состояние; kv
, в противоположность k, никак не является целым числом.

В конце концов, разглядим молекулы типа шарового волчка. Сюда относятся молекулы с симметрией какой-нибудь из кубических групп. Такие молекулы владеют одно-, дву- и трехкратными частотами. Вырождение колебательных уровней, как постоянно, отчасти снимается ангармоничностью; опосля учета этих эффектов остаются, кроме невырожденных, только дву- и трехкратно вырожденные уровни. Мы будем на данный момент гласить конкретно о этих расщепленных ангармоничностью уровнях.

Просто созидать, что у молекул типа шарового волчка средний колебательный момент отсутствует не только лишь в невырожденных, да и в дважды вырожденных колебательных состояниях. Это следует уже из обычных суждений, основанных на свойствах симметрии. Вправду, векторы средних моментов в 2-ух состояниях, относящихся к одному вырожденному уровню энергии, должны могли быть преобразовываться друг в друга при всех преобразованиях симметрии молекулы. Но ни одна из кубических групп симметрии не допускает существования 2-ух преобразующихся только друг в друга направлений; преобразуются друг в друга только совокупы не наименее чем 3-х направлений.

Из этих же суждений следует, что в состояниях, соответственных трехкратно вырожденным колебательным уровням, средний колебательный момент отличен от нуля. Опосля усреднения по колебательному состоянию этот момент представится оператором, изображающимся матрицей, элементы которой соответствуют переходам меж 3-мя взаимно вырожденными состояниями. В согласовании с числом таковых состояний этот оператор должен иметь вид где 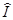— оператор момента, равного единице (для которого 2l + 1 = 3), а z — соответствующая для данного осциллирующего уровня неизменная. Гамильтониан вращательного движения молекулы

опосля такового усреднения преобразуется в оператор

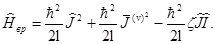(3.6)

Собственные значения первого члена — это рядовая вращательная энергия

,

а 2-ой член дает несущественную постоянную, не зависящую от вращательного квантового числа. Крайний же член в (3.6) дает разыскиваемую энергию кориолисова расщепления осциллирующего уровня. Собственные значения величины Л рассчитываются обыденным образом; она может иметь (при данном J) три разных значения (соответственных значениям вектора I + J, равным J + 1, J — 1, J). В итоге найдем

, , .

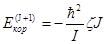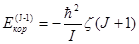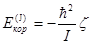Перечень литературы

Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. Пособие для вузов. В10 т. Т III. Квантовая механика (нерелятивистская теория) – М.: Наука, 1989 г.

Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. Пособие для вузов. В10 т. Т V. Статистическая физика 1-ая ч. – М., 1976 г.

Кубо Р., Статистическая механика. -М.:, 1967 г.

Сивухин Д.В. Общий курс физики, т.2, Термодинамика и молекулярная физика. ФИЗМАТЛИТ, 2003 г.

[1]
Эффекты квантования вращения могли бы наблюдаться только у метана СН4
, где они должны показаться при температурах около 50° К.

[2]
Так, у Н2
О (равнобедренный треугольник) s=2; у NН3
(треугольная верная пирамида) s=3;
у СН4
(тетраэдр) s=12; у C6
H6
(верный шестиугольник) s=12.

[3]
Так, два -взаимно перпендикулярных поперечных колебания с разностью фаз в я/2 можно разглядывать как незапятнанное вращение изогнутой молекулы вокруг

[4]
Поступательное движение предполагается отделенным с самого начала выбором системы координат, в какой центр инерции молекулы лежит.

]]>