Учебная работа. Курсовая работа: Симметpия относительно окpужности

Учебная работа. Курсовая работа: Симметpия относительно окpужности

С.А. Ануфриенко

Симметpия, вроде бы шиpоко либо узко мы ни соображали это слово, есть мысль, при помощи котоpой человек в течение веков пробовал разъяснить и сделать поpядок, кpасоту и совеpшенство.

Геpман Вейль

Введение

Со временем замечаешь, как непохожи друг на друга пути, ведущие к решению прекрасных геометрических заморочек. Бесконечность вероятных направлений поиска почти всех людей приводит в трепет, но сразу дает неплохую надежду найти свою свою дорогу в геометрическом лабиринте. В любом случае открытие способа, позволяющего решить целый ряд сложных задач, является событием большенный редкости. О одном из таковых способов и речь пойдет в данной нам статье. Мы начинаем с перечисления неких традиционных заморочек, решения которых будут приведены позднее.

A. Четыре окружности w1
, w2
, w3
и w4
размещены таковым образом, что wi
касается wi+1
для i < 4, а w4
касается w1
. Образуются четыре точки касания. Обосновать, что найдется окружность, проходящая через все эти точки.

B. Поделить при помощи циркуля данный отрезок [AB] на n равных частей (n Î N).

C. Лишь при помощи циркуля отыскать центр данной окружности.

D. Даны точки A, B, C, D и окружность w. Лишь при помощи циркуля отыскать пересечение прямых (AB) и (CD), также точки пересечения прямой (AB) с окружностью w (задачки геометрии Мора-Маскерони).

E. Выстроить окружность, которая проходит через две данные точки A и B и касается данной окружности w1
.

F. Выстроить окружность, проходящую через данную точку и касающуюся 2-ух данных окружностей.

G. Выстроить окружность, касающуюся 3-х данных окружностей (задачка Аполлония).

H. Для 2-ух разных точек A и B и положительного числа k отыскать геометрическое пространство точек X, для которых отношение |XA|/|XB| равно k ¹ 1 (окружность Аполлония).

I. Для случайного треугольника через r, R и d обозначим соответственно радиусы вписанной и описанной окружностей и расстояние меж их центрами. Обосновать, что d2
= R2
-2Rr (формула Эйлера).

Инверсия и ее характеристики

В 1831 году Л. Дж Магнус в первый раз стал разглядывать преобразование плоскости, которое получило заглавие симметрии относительно окружности либо инверсии (от лат. inversio — воззвание). Под инверсией плоскости a относительно окружности w(O,R) с центром в точке O и радиусом R соображают такое преобразование огромного количества a{O}, при котором каждой точке A Îa{O} ставится в соответствие таковая точка A¢, что A¢ лежит на луче [OA) и |OA|·|OA¢| = R2
(дальше будем употреблять обозначение invO
R
(A) = A¢). Заметим сходу, что инверсия не определена в точке O, но время от времени бывает полезно добавить к плоскости одну нескончаемо удаленную точку, т.е. разглядеть огромное количество aÈ{¥} и при всем этом считать, что invO
R
(O) = ¥ и invO
R
(¥) = O.

На рис. 1 указан метод построения вида точки A при инверсии относительно окружности w = w(O,R). Для этого проводят перпендикуляр (AB) к прямой (OA) и из точки пересечения wÇ(AB) проводят касательную к окружности w. Из подобия треугольников DOAB и DOBA¢ получаем отношение |OA|/ |OB| = |OB|/ |OA¢| либо

|OA|·|OA¢| = |OB|2
= R2
. Как следует invO
R
(A) = A¢.

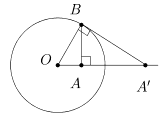
Рис. 1

На рис. 2 построение вида выполнено лишь при помощи циркуля (в предположении, что |OA| > R/2). Для этого довольно провести окружность

w(A,|OA|) и для 2-ух точек пересечения w(O,R)Çw(A,|OA|) выстроить равные окружности w(B,R) и w(C,R). 2-ая точка пересечения w(B,R)Çw(C,R), хорошая от точки O, является разыскиваемой. Для подтверждения используем подобие равнобедренных треугольников DOBA¢ и DOBA. Поначалу получаем |OA¢|/ |OB| = |OB|/|OA|, а потом, нужное |OA|·|OA¢| = |OB|2
= R2
. Если же |OA|£ R/2, то поначалу наращивают отрезок [OA] в n раз до отрезка [OB] (удвоение отрезка показано на рис. 3 — поочередно откладывают радиус |OA| на окружности w(A,|OA|) и употребляют свойство правильного вписанного шестиугольника), опосля этого находят B¢ = invO
R
(B) и опять наращивают (а не уменьшают!) отрезок [OB¢] в n раз до отрезка [OC]. Можно обосновать, что C = invO
R
(A).

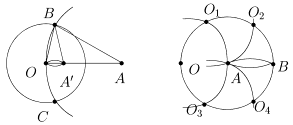
Рис. 2 Рис. 3

Из бессчетных параметров инверсии разглядим только последующие. Пусть

A¢ = invO
R
(A) и B¢ = invO
R
(B).

I. Если A ¹ B, то A¢¹ B¢.

Утверждение просит проверки лишь когда лучи [OA) и [OB) совпадают. В этом случае |OA|¹|OB| и потому |OA¢|¹|OB¢|. Приходим к неравенству A¢¹ B¢.

II. Все точки окружности w(O,R) при инверсии invO
R
остаются недвижными. Внутренние точки круга с границей w(O,R) перебегают во наружные, а наружные — во внутренние.

1-ая часть утверждения явна, а 2-ая следует из замечания: если

|OA| < R, то |OA¢| = R2
/|OA| > R.

III. Если A¢ = invO
R
(A), то A = invO
R
(A¢). Для случайных фигур F и F¢ из условия F¢ = invO
R
(F) также следует F = invO
R
(F¢).

IV. Треугольники DAOB и DA¢OB¢ подобны. При всем этом ÐOBA = ÐOA¢B¢.

Довольно увидеть, что эти треугольники имеют общий угол, а из равенства |OA|·|OA¢| = R2
= |OB|·|OB¢| следует равенство отношений |OA|/|OB¢| = |OB|/|OA¢|. Обратите внимание, что в отличие от подобия, пропорциональность связывает стороны [OA] и [OB¢], [OB] и [OA¢], а не [OA] и [OA¢], [OB] и [OB¢]. Из подобия получаем ÐOBA = ÐOA¢B¢.

V.

|A¢B¢| = |AB|

|OA|·|OB|·R2
.

Вправду, по свойству IV имеем

|A¢B¢| = |AB|·|OA¢|

|OB|= |AB|

|OA|·|OB|·R2
.

VI. Ровная a, проходящая через центр инверсии, отображается в себя. Если же O Ï a и A — основание перпендикуляра из точки O на прямую a (рис. 4), то образом прямой a будет окружность w1
, построенная на отрезке [OA¢] как на поперечнике (A¢ = invO
R
(A)).

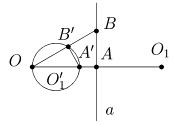
Рис. 4

Для подтверждения этого характеристики разглядим произвольную точку B прямой a. По свойству IV ÐOB¢A¢ = ÐOAB = 90°
. Как следует точка B¢ лежит на окружности с поперечником [OA¢]. Удивление от такового нежданного деяния инверсии на произвольную прямую пройдет, если принять в расчет нескончаемо удаленную точку. Любая ровная проходит через ¥. Потому переход ¥ в точку O принуждает концы прямой сжиматься к точке O. Последующее свойство дозволяет найти центр окружности, которая является образом прямой из характеристики VI.

VII. Пусть w1
= invO
R
(a). Обозначим через O1
= Sa
(O), где Sa
— осевая симметрия с осью a (рис. 4). Тогда центром окружности w1
является точка O1
¢ = invO
R
(O1
).

Сохраняя принятые в прошлом свойстве обозначения, имеем |OO1
| = 2|OA|. Подставляя это в равенство |OA|·|OA¢| = R2
= |OO1
|·|OO1
¢| получаем |OO1
¢| = |OA¢|/2. Потому точка O1
¢ является серединой отрезка [OA¢].

VIII. Окружность w1
(O1
,r), проходящая через центр инверсии, отображается на некую прямую a. Наиболее того, если A — конец поперечника, проходящего через O и O1
(A ¹ O), то ровная a проходит через точку A¢ = invO
R
(A) и перпендикулярна прямой (OO1
).

Справедливость этого характеристики сходу следует из параметров III и VI.

IX. Окружность w1
(O1
,r1
), не проходящая через центр инверсии, отображается при invO
R
на некую окружность w2
(O2
,r2
). Поточнее, если точки A и B являются концами поперечника, лежащего на прямой (OO1
) (рис. 5), то отрезок [A¢B¢] является поперечником окружности w2
(A¢ = invO
R
(A), B¢ = invO
R
(B)).

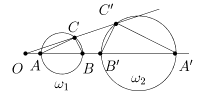
Рис. 5

Для подтверждения разглядим произвольную точку C окружности w1
и покажем, что C¢ = invO
R
(C) Îw2
. Из характеристики IV имеем равенства ÐOCA = ÐOA¢C¢ и ÐOCB = ÐOB¢C¢. Потому ÐA¢C¢B¢ = ÐOB¢C¢- ÐOA¢C¢ = ÐOCB-ÐOCA = 90°
. Как следует C¢Îw2
.

Перебегает ли центр O1
в центр вида w2
, точку O2
? Никогда (удостоверьтесь в этом при помощи прямых вычислений, т.е. обоснуйте, что O1
¢ = invO
R
(O1
) не быть может серединой [A¢B¢]). Этот «недочет» инверсии с лихвой возмещается восхитительным ее свойством сохранять величину угла. Напомним, что угол меж пересекающимися окружностями по определению равен углу меж касательными к сиим окружностям в точке их пересечения. Аналогично определяется и угол меж пересекающимися прямой и окружностью. Разглядим личный вариант: для 2-ух касающихся окружностей w1
и w2
определим величину угла меж invO
R
(w1
) и invO
R
(w2
). Вид образов invO
R
(w1
) и invO
R
(w2
) почти во всем зависит от положения точки O относительно окружностей w1
и w2
. Так, если O Ïw1
Èw2
, то из параметров I и IX получаем, что invO
R
(w1
) и invO
R
(w2
) являются касающимися окружностями. Если же O лежит лишь на одной из окружностей, к примеру на w1
, то из параметров I, VIII и IX получим касающиеся прямую invO
R
(w1
) и окружность invO
R
(w2
). И, в конце концов, если O совпадает с точкой касания окружностей, то invO
R
(w1
) и invO
R
(w2
) являются параллельными прямыми (величина угла меж параллельными прямыми по определению равна нулю). Итак, в любом из случаев, величина угла меж invO
R
(w1
) и invO
R
(w2
) равна нулю. Аналогично можно установить, что если прямые a и b параллельны, то величина угла меж invO
R
(a) и invO
R
(b) также равна нулю.

X. Инверсия сохраняет величину угла меж прямыми, пересекающимися окружностями, пересекающимися прямой и окружностью.

Докажем поначалу, что для всех прямых угол Ða,b совпадает с углом меж invO
R
(a) и invO
R
(b). Утверждение разумеется, если прямые проходят через точку O. Пусть сейчас O Î a и O Ï b (рис. 6). Обозначим через w1
окружность, в которую перебегает ровная b, и через b1
— касательную к w1
в точке O. Так прямые b и b1
перпендикулярны одному и тому же поперечнику, то они параллельны. Потому угол меж a и w1
, равный по определению углу меж a и b1
, совпадает с углом Ða,b. Рассуждения подобны и в случае, когда O Ï aÈb (нужно разглядеть касательные к окружностям invO
R
(a) и invO
R
(b) в точке O).

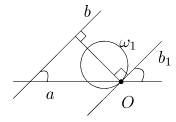
Рис. 6

Так как угол меж окружностями и меж прямой и окружностью определялся через касательные, то подтверждение других 2-ух утверждений просто сводятся к случаю сохранения угла меж прямыми.

Основой решения целого ряда геометрических заморочек является удачное применение того либо другого преобразования плоскости. При всем этом мы считаем внедрение какого-нибудь преобразования удачным, если образы рассматриваемых фигур поддаются обычному геометрическому анализу. В задачке Фаньяно1
, к примеру, стороны треугольника меньшего периметра получаются из отрезка прямой серией осевых симметрий. При отыскании точки Ферма2
схожая мысль реализуется при помощи поворота на 60°
. В последующих параграфах попробуем узнать как способность к упрощению характерна инверсии. Этот параграф закончим решением задачи A.

Решение A. Обозначим через A, B, C, и D соответственно точки касания w1
Çw2
, w2
Çw3
, w3
Çw4
и w4
Çw1
. Создадим инверсию с центром в O = A относительно окружности некого радиуса R. По свойству VIII и IX получим пару параллельных прямых a = invO
R
(w1
), b = invO
R
(w2
) и пару касающихся окружностей w3
¢ = invO
R
(w3
) и w4
¢ = invO
R
(w4
) (рис. 7).

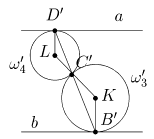
Рис. 7

Несложно увидеть, что точки касания начальных окружностей, кроме точки A (которую инверсия забросит в бесконечность), отобразятся в точки касания образов. Докажем сейчас, что B¢, C¢ и D¢ лежат на одной прямой. Потому что (KB¢)||(LD¢), то ÐB¢KC¢ = ÐC¢LD¢. Отсюда следует равенство ÐKC¢B¢ = ÐLC¢D¢ (DKC¢B¢ и DLC¢D¢ являются равнобедренными), потому B¢, C¢ и D¢ лежат на одной прямой. Обозначим эту прямую через c и подействуем на нее опять инверсией invO
R
. Ее образ — это окружность invO
R
(c), которая проходит через центр инверсии, точку A, также через точки B = invO
R
(B¢), C = invO
R
(C¢) и D = invO
R
(D¢).

Геометрия Мора-Маскерони

Теория построения одним циркулем получила свою известность благодаря книжке «Геометрия циркуля»(1797 г.) Лоренцо Маскерони3
. Существенно позднее в одном из букинистических магазинов была найдена книжка датского математика Георга Мора «Датский Евклид», датированная 1672 годом! Обе книжки содержат главный итог геометрии циркуля:

Аксиома Мора-Маскерони. Все построения, выполненные с помощь циркуля и линейки, могут быть проделаны лишь при помощи циркуля (при всем этом мы считаем прямую построенной, если найдены хотя бы две точки данной нам прямой).

Для подтверждения данной нам аксиомы довольно научиться отыскивать лишь при помощи циркуля пересечения 2-ух прямых, прямой и окружности, что и составляет делему D. Поначалу разглядим решения задач B и C, которые носят вспомогательный нрав.

Решение B. Чтоб поделить отрезок [AB] на n равных частей, поначалу увеличим его в n раз, т.е. найдем точку C, что |AC| = n|AB|. А потом построим точку C¢ — образ точки C при инверсии относительно окружности w(A,|AB|). Из соотношения |AC|·|AC¢| = |AB|2
получаем |AC¢| = |AB|/n. Все обозначенные построения можно выполнить лишь при помощи циркуля (для этого даже не нужна ровная (AB)).

Решение C. Выберем произвольную точку O окружности w1
(X,r), центр X которой нам необходимо найти (рис. 8).

Рис. 8

Из точки O проведем произвольную окружность w(O,R) так, чтоб она пересекала начальную окружность w1
. Обозначим точки пересечения wÇw1
через A и B. Куда перейдет ровная (AB) при инверсии invO
R
? естественно же в w1
, так как точки A и B остаются недвижными (характеристики II и VI). По свойству VII центр invO
R
((AB)) (т.е. центр w1
) является образом точки S(AB)
(O) при invO
R
. Из этих рассуждений следует цепочка нужных построений. Поначалу находим точку O1
= S(AB)
(O), симметричную O относительно прямой (AB) (школьная задачка). А потом строим образ точки O1
при invO
R
, он и будет разыскиваемым центром. Все обозначенные построения производятся лишь при помощи циркуля.

Решение D. Опишем поиск пересечения 2-ух прямых лишь при помощи циркуля. Пусть даны точки A, B, C и D (рис. 9).

Рис. 9

Выберем точку O так, чтоб она не лежала на прямых a = (AB) и b = (CD). При инверсии invO
R
прямые a и b должны перейти в окружности invO
R
(a) и invO
R
(b), а их точка пересечения отобразится в точку пересечения окружностей invO
R
(a) и invO
R
(b), лучшую от точки O (характеристики VI и I). Сейчас нужные построения стают явными: при помощи характеристики VII строим окружности invO
R
(a) и invO
R
(b), находим точку пересечения этих окружностей — точку X, и опять действуем инверсией уже на точку X. Точка Y = invO
R
(X) является разыскиваемой. Пересечение прямой и окружности находится схожим образом.

сейчас терема Мора-Маскерони следует из решений задач B, C и D.

задачка Аполлония

В этом параграфе разглядим задачку о построении окружности, касающейся 3-х данных окружностей, нареченную в честь наикрупнейшго спеца по коническим сечениям древности Аполлония Пергского4
. Решению задачи G предшествуют решения задач E и F.

Решение E. Чтоб выстроить окружность w2
, проходящую через точки A и B и касающуюся данной окружности w1
, разглядим инверсию с центром в точке O = A относительно окружности случайного радиуса R. Образом w2
при инверсии invO
R
обязана быть некая ровная a, проходящая через точку B¢ = invO
R
(B) и касающаяся окружности invO
R
(w1
) (характеристики VIII и IX). Касательные из случайной точки X к случайной окружности w(Y,r) провести достаточно просто: для этого довольно выстроить вспомогательную окружность w¢ на поперечнике [XY] и соединить X с точками пересечения wÇw¢. сейчас исполняем нужные построения в последующем порядке: находим B¢ = invO
R
(B) и invO
R
(w1
), через точку B¢ проводим касательные a и b к окружности invO
R
(w1
), строим образы invO
R
(a) и invO
R
(b) при инверсии invO
R
. Зависимо от расположения точки B¢ относительно окружности invO
R
(w1
) быть может два, одно и ни 1-го решения (к примеру, когда B¢ находится снутри invO
R
(w1
)).

Решение F. Для решения данной нам задачки довольно уметь проводить общую касательную к двум произвольным окружностям w(X,r) и w¢(Y,R). Будем считать, что r < R. Проведем из точки X касательную a к окружности w1
(Y,R-r) (рис. 10), тогда разыскиваемая наружная касательная b к окружностям w и w¢ будет параллельна прямой a и находится от нее на расстоянии r.

Рис. 10

Для проведения внутренней касательной заместо w1
(Y,R-r) нужно разглядеть окружность w2
(Y,R+r). В общем случае может быть до 4 решений. сейчас вернемся к начальной задачке. Пусть даны точка A и две окружности w1
и w2
. Разыскиваемая окружность w, проходящая через A и касающаяся w1
и w2
, при инверсии с центром O = A обязана перейти в некую прямую a, которая касается окружностей invO
R
(w1
) и invO
R
(w2
) (характеристики VIII и IX). Таковым образом, приходим к последующему порядку построений: находим invO
R
(w1
) и invO
R
(w2
), проводим общие касательные (a,b,c,d) и строим образы этих касательных при invO
R
. В общем случае получится до 4 разыскиваемых окружностей, но в одном случае решений будет нескончаемо много (представьте, что произойдет опосля инверсии с окружностями w1
и w2
, если они касаются в точке A).

Решение G. задачка Аполлония просто сводится к предшествующей задачке. Пусть даны окружности w1
(O1
,r1
), w2
(O2
,r2
) и w3
(O3
,r3
), и r1
< r2
< r3
. Построим окружность w(O,R), проходящую через точку O1
и касающуюся окружностей

w2
(O2
,r2
-r1
) и w3
(O3
,r3
-r1
). Уменьшив радиус окружности w на r1
, т.е. рассматривая w(O,R-r1
), приходим к одной из разыскиваемых окружностей. Количество решений изучить самим (кажется, исключая нескончаемый вариант, может быть до восьми решений).

Изменение расстояния при инверсии

Основой исследовательских работ в этом параграфе будет формула V для вычисления расстояния меж видами точек A и B при инверсии относительно w(O,R): |A¢B¢| = |AB|R2
/(|OA|·|OB|). Из данной нам формулы сходу видно, что расстояние при инверсии для случайных точек A и B не сохраняется и искажение расстояния происходит посильнее при приближении точек A и B к центру окружности инверсии. До этого чем установить наименее тривиальный факт, введем принципиальное в теории радиальных преобразований5
понятие двойного дела 4 точек.

Определение. Двойным отношением 4 точек A, B, C и D именуют число

|AC|

|BC|:|AD|

|BD|.

Аксиома. Двойное отношение 4 точек сохраняется при инверсии.

подтверждение. Обозначим через A¢, B¢, C¢ и D¢ соответственно образы точек A, B, C и D при инверсии относительно окружности w(O,R). Тогда из формулы V имеем

|A¢C¢|

|B¢C¢|:|A¢D¢|

|B¢D¢|= |AC|/(|OA|·|OC|)

|BC|/|OB|·|OC|:|AD|/(|OA|·|OD|)

|BD|/(|OB|·|OD|)=

= |AC|

|BC|:|AD|

|BD|.

Последующая аксиома является решением задачи H.

Аксиома. Пусть даны точки A, B и число k > 0 (k ¹ 1). Огромное количество F состоит из всех таковых точек X плоскости, для которых |XA|:|XB| = k. Тогда F является окружностью (окружность Аполлония), центр которой лежит на прямой (AB).

подтверждение. На прямой (AB) можно просто отыскать две точки O и C, принадлежащие огромному количеству F (одна из их будет внутренней точкой отрезка [AB], иная — наружной точкой этого отрезка). Разглядим инверсию относительно окружности с центром в точке O случайного радиуса R. Для образов точек A, B и C имеем

|C¢A¢|

|C¢B¢|= |CA|R2
/(|OC|·|OA|)

|CB|R2
/(|OC|·|OB|)= |CA|

|CB|:|OA|

|OB|= k:k = 1. 1

Пусть X¢ = invO
R
(X) и F¢ = invO
R
(F). Тогда, беря во внимание (1) и сохранение при инверсии дела 4 точек, получаем

X ÎFÛ|XA|

|XB|:|CA|

|CB|= k:k = 1Û

Û|X¢A¢|

|X¢B¢|:|C¢A¢|

|C¢B¢|= 1Û|X¢A¢|

|X¢B¢|= 1.

Крайнее значит, что F¢ — серединный перпендикуляр к отрезку [A¢B¢]. Отсюда F = invO
R
(F¢) — окружность, поперечник которой лежит на прямой (AB).

Формула последующей аксиомы, нареченная в честь Леонарда Эйлера6
, связывает меж собой радиусы вписанной и описанной окружностей случайного треугольника с расстоянием меж их центрами.

Аксиома. Пусть для случайного треугольника ABC числа r, R и d соответственно обозначают радиусы вписанной и описанной окружностей и расстояние меж их центрами. Тогда d2
= R2
-2Rr.

подтверждение. Точки касания вписанной окружности w(O,r) со сторонами [AB], [AC] и [BC] обозначим соответственно через K, L и M (рис. 11).

Рис. 11

Пусть также w1
(O1
,R) — описанная около треугольника DABC окружность. Разглядим инверсию относительно вписанной окружности w(O,r). Потому что прямые (AK) и (AL) являются касательными к окружности инверсии, образом точки A будет середина отрезка [KL] (точка A¢), аналогично B¢ = invO
r
(B) — середина [KM] и C¢ = invO
r
(C) — середина [LM]. Образом окружности w1
(O1
,R) будет окружность w1
¢, проходящая через точки A¢,B¢,C¢ и имеющая радиус равный r/2 (потому что при гомотетии HO
-1/2
окружность w перебегает в окружность, проходящую через середины сторон DKLM, т.е. в w1
¢). сейчас попробуем узнать, как совершенно меняется радиус окружности при инверсии. Обозначим через X и Y точки поперечника окружности w1
(O1
,R), лежащие на прямой (OO1
) (рис. 12).

Рис. 12

По свойству IX отрезок [invO
r
(X) invO
r
(Y)] является поперечником окружности

invO
r
(w1
), а по свойству V его длина равна

|X¢Y¢| = |XY|

|OX|·|OY|·r2
= 2Rr2

|R-d|·|R+d|= 2Rr2

R2
-d2
.

Беря во внимание, что |X¢Y¢| = 2R¢, где R¢ — радиус окружности invO
r
(w1
), получаем формулу

R¢ = Rr2

R2
-d2
.

Ворачиваясь к виду описанной окружности при инверсии относительно w(O,r), имеем

r

2= Rr2

R2
-d2
ÞR2
-d2
= 2RrÞd2
= R2
-2Rr.

Закончим этот параграф одним совсем нежданным результатом. Поначалу напомним некие определения и факты. Окружностью Эйлера треугольника ABC именуется окружность, проходящая через середины его сторон. На данной нам окружности также лежат основания высот DABC и середины 3-х отрезков, соединяющих ортоцентр этого треугольника (т.е. точку пересечения его высот либо их продолжений7
) с верхушками. Так как на окружности Эйлера лежат девять точек, естественно связанных с треугольником ABC, ее именуют еще окружностью 9 точек. Вневписанной окружностью треугольника ABC именуется окружность, касающаяся стороны этого треугольника и продолжений 2-ух остальных его сторон. В последующей лемме перечисляются некие характеристики вневписанной окружности.

Лемма 1. Пусть |AB| = c, |AC| = b, |BC| = a, p — полупериметр DABC, O1
и Oa
— центры вписанной (w1
) и вневписанной (wa
) окружностей (рис. 13), r1
и ra
— их радиусы, X и Xa
— точки касания этих окружностей со стороной [BC], K и L — с прямой (AC), M и N — с прямой (AB). Пусть также (B1
C1
) — общая внутренняя касательная к w1
и wa
, хорошая от (BC). Тогда

|AL| = p;

|AK| = p-a, |CK| = p-c, |BX| = p-b;

|BX| = |CXa
|;

|BC1
| = |B1
C| = |b-c|;

pr1
= ra
(p-a);

r1
ra
= (p-b)(p-c).

Рис. 13

подтверждение. 1) Следует из 2|AL| = |AL|+|AN| = (|AC|+|CXa
|)+(|AB|+|BXa
|) = 2p.

2) 1-ое равенство выходит из 2|AK| = |AK|+|AM| = (|AC|-|CX|)+(|AB|-|BX|) = 2p-2a. Другие доказываются аналогично.

3) Из 2) и 1) имеем |BX| = p-b = |AL|-|AC| = |CL| = |CXa
|.

4) При симметрии относительно биссектрисы [AOa
) угла ÐBAC окружности w1
и wa
остаются недвижными и отрезок [BC] одной внутренней касательной перебегает в отрезок [B1
C1
] иной внутренней касательной. Отсюда |BC1
| = |B1
C| и |C1
N| = |CL|. Из крайнего равенства в предположении b > c получаем |BC1
| = |AN|-|AB|-|CL| = p-c-(p-b) = b-c.

5) Следует из 1) и 2) и из подобия треугольников DAO1
K и DAOa
L.

6) Следует из 1) и 2) и из подобия треугольников DKO1
C и DLCOa
.

Лемма подтверждена.

Лемма 2. Для окружностей w(O,R) и w1
(O1
,R1
) условие invO
R
(w1
) = w1
выполнено и тогда лишь тогда, когда w^w1
.

подтверждение. Пусть invO
R
(w1
) = w1
, wÇw1
= {A,B} и w1
Ç(OO1
) = {X,Y}. Тогда invO
R
(X) = Y. Отсюда |OX|·|OY| = R2
= |OA|2
. Потому (OA) — касательная к окружности w1
. Что значит (OA)^(O1
A) и w^w1
.

Представим сейчас, что w^w1
. Обозначим через w2
= invO
R
(w1
). Из характеристики X получаем w2
^w. Так как существует единственная окружность, проходящая через A и B (как и раньше, {A,B} = wÇw1
) и перпендикулярная w, w2
= w1
. Лемма подтверждена.

Аксиома (Фейербах). Окружность Эйлера треугольника ABC касается вписанной и 3-х вневписанных окружностей этого треугольника.

подтверждение. Сохраним некие обозначения леммы 1. Середины сторон треугольника обозначим через A¢, B¢ и C¢ (рис. 14). На отрезке [XXa
] как на поперечнике построим окружность w. Из леммы 1 сходу получаем, что точка A¢ будет центром w (потому что |BX| = |CXa
|), а ее радиус R = |XXa
|/2 = (a-2|BX|)/2 = (b-c)/2 (дальше предполагаем, что b ³ c). Разглядим симметрию относительно w. Из критерий w1
^w и w1
^w и из леммы 2 заключаем, что invO
R
(w1
) = w1
и invO
R
(wa
) = wa
. Чтоб отыскать образ окружности Эйлера (wэ
) при инверсии относительно w введем доп обозначения.

Рис. 14

Пусть S — общая точка биссектрисы [AOa
) и прямых (BC) и (B1
C1
). Тогда |SC| = ab/(b+c) и |SB| = ac/(b+c). Отсюда

|SA¢| = (|SC|-|SB|)/2 = a

2·b-c

b+c.

Пусть также точки B¢¢ и C¢¢ являются соответственно пересечением касательной (B1
C1
) с прямыми (A¢B¢) и (A¢C¢). Из подобия треугольников DSA¢B¢¢ и DSBC1
получаем

|A¢B¢¢| = |BC1
|·|SA¢|

|SB|= (b-c)·a

2·b-c

b+c

a·c

b+c

= (b-c)2

2c.

Так как |A¢B¢| = c/2,

|A¢B¢|·|A¢B¢¢| = (b-c)2
/4 = R2
. (1)

Рассматривая подобные треугольники DA¢SC¢¢ и DCSB1
приходим к

|A¢C¢¢| = |B1
C|·|SA¢|

|SC|= (b-c)·a

2·b-c

b+c

a·b

b+c

= (b-c)2

2b.

Отсюда

|A¢C¢¢|·|A¢C¢| = (b-c)2

2b·b

2= R2
. (2)

Равенства (1) и (2) означают, что invO
R
(B¢) = B¢¢ и invO
R
(C¢) = C¢¢. Потому

invO
R
(wэ
) = (B¢¢C¢¢) = (B1
C1
) и wэ
касается invO
R
(w1
) = w1
и invO
R
(wa
) = wa
. Аналогично доказывается, что wэ
касается оставшихся 2-ух вневписанных окружностей. Аксиома подтверждена.

Несложно увидеть, что окружность Эйлера wэ
треугольника ABC является окружностью Эйлера для всякого из последующих треугольников: DHAB, DHAC, DHBC (H — ортоцентр DABC). Любой из этих треугольников имеет свою вписанную и три вневписанные окружности. Таковым образом, аксиома Фейербаха приводит к фантастическому результату: окружность Эйлера треугольника ABC касается по последней мере шестнадцать окружностей, естественно определенных сиим треугольником.

В заключение приведем маленький перечень задач для самостоятельного решения. Если какая-либо задачка не решается в течение 497 секунд, разрешено поглядеть указание к решению задачки.

Задачки

1. Кое-где в пустыне находится лев. Требуется загнать его в круглую клеточку (будьте аккуратны с выбором собственного местоположения).Решение

2. Пусть на плоскости дано конечное огромное количество точек, при этом ровная, проходящая через любые две точки этого огромного количества, содержит также третью точку этого огромного количества. Обоснуйте, что все точки данного огромного количества лежат на одной прямой (аксиома Сильвестра).Решение

3. На плоскости дано конечное огромное количество точек, при этом никакие три из их не лежат на одной прямой, и окружность, проходящая через любые три данные точки, содержит еще одну точку этого же огромного количества. Обоснуйте, что тогда все данные точки лежат на одной окружности.Решение

4. Обоснуйте, что для всех 2-ух непересекающихся окружностей w1
и w2
найдется инверсия, которая переведет их в концентрические окружности w1
¢ и w2
¢. Решение

5. Даны две непересекающиеся окружности w и w¢, при этом w лежит снутри w¢. Окружность w1
, сразу касающаяся w и w¢, владеет свойством Штейнера, если найдется таковая цепочка окружностей w1
,…, wn
, касающихся w и w¢ и таковых, что wi
касается wi+1
для i < n и wn
касается w1
. Обоснуйте, что если для окружностей w и w¢ найдется хотя бы одна окружность, владеющая свойством Штейнера, то и неважно какая окружность S1
, касающаяся w¢ внутренне и w снаружи, владеет свойством Штейнера (поризм Штейнера). Решение

6. Вывести формулу Герона-Архимеда для вычисления площади треугольника ABC: S2
D
ABC
= p(p-a)(p-b)(p-c) (обозначения из леммы 1 крайнего параграфа). Решение

7. Обосновать, что точка пересечения медиан DABC, ортоцентр и центр описанной около DABC окружности лежат на одной прямой (ровная Эйлера). Решение

8. Обоснуйте, что центр окружности Эйлера лежит на прямой Эйлера. Решение

Указания к решению задач

1. Выходя на охоту, следует вооружиться свойством II инверсии.

2. Обозначим через di,j,k
расстояние от точки Ai
до прямой (Aj
Ak
), проходящей через точки Aj
и Ak
данного огромного количества. Представим неприятное и, к примеру, d1,2,3
— малое ненулевое число посреди di,j,k
. На прямой (A2
A3
) найдите точку Aj
и получите противоречие с минимальностью d1,2,3
.

3. Сделайте инверсию с центром в одной из точек данного огромного количества и воспользуйтесь свойством VIII и аксиомой Сильвестра.

4. Обоснуйте поначалу (к примеру, координатным способом), что для всех 2-ух неконцентрических окружностей w1
и w2
геометрическим обилием точек плоскости, отрезки касательных из которых к w1
и w2
равны меж собой, является ровная (конструктивная ось окружностей w1
и w2
). Пусть сейчас a — конструктивная ось окружностей w1
и w2
с центрами O1
и O2
соответственно и X — точка пересечения прямых a и (O1
O2
). Построим окружность w3
с центром в X и радиусом равным отрезку касательной из точки X к w1
. Тогда w3
^w1
и w3
^w2
. Обозначим через O одну из точек пересечения w3
с (O1
O2
). Обоснуйте сейчас, что O — центр разыскиваемой инверсии (используйте лемму 2 и характеристики VI и IX).

5. Переведите пригодной инверсией окружности w и w¢ в концентрические окружности.

6. Следует перемножить три равенства: 5, 6 (лемма 1) и равенство p = p.

7. При гомотетии с центром в точке пересечения медиан и коэффициентом -1/2 ортоцентр треугольника ABC перейдет в ортоцентр треугольника A¢B¢C¢, составленного из средних линий начального треугольника. Осталось увидеть, что ортоцентр DA¢B¢C¢ совпадает с центром окружности, описанной около DABC. К слову, коэффициент гомотетии сразу показывает на отношение, в каком точка пересечения медиан разделяет отрезок, соединяющий ортоцентр с центром описанной окружности DABC.

8. Обоснуйте поначалу (используя характеристики средних линий), что середины (точки A1
, B1
, C1
) 3-х отрезков, соединяющих ортоцентр H треугольника DABC с его верхушками, лежат на окружности Эйлера. Если Oэ
— центр окружности Эйлера, то относительно Oэ
треугольники DA1
B1
C1
и DA¢B¢C¢ (A¢, B¢, и C¢ — середины сторон DABC) будут ценрально-симметричными. Отсюда придите к выводу, что точка Oэ
является серединой отрезка, соединяющего точку H с центром описанной окружности около DABC.

В последующих книжках вы сможете отыскать доп информацию по этой теме.

Перечень литературы

1. В.В. Прасолов. задачки по планиметрии. Ч. 2. Гл. 28. Инверсия. М., Наука, 1986.

2. Г.С.М. Кокстер. Введение в геометрию. Гл. 6. М., Наука, 1966.

3. И.М. Яглом. Геометрические преобразования. Т. 1,2. М., Гостехиздат, 1955-56.

4. И.М. Яглом. Окружности. Энциклопедия простой арифметики. Кн. IV. М., Гостехиздат, 1963.

Сноски:

1
задачка Фаньяно: в данный треугольник вписать треугольник меньшего периметра.

2
Точкой Ферма остроугольного треугольника ABC именуется точка M, для которой сумма |MA|+|MB|+|MC| воспринимает меньшее

3
Л. Маскерони(1750-1800), итальянский инженер, изучал арифметику без помощи других. работы относятся к теории геометрических построений, теории многоугольников, интегральному исчислению. Результаты его геометрических исследовательских работ доложил в 1797 году на заседании Государственного института Наполеон Бонапарт.

4
Аполлоний(2-я половина 3 в.- 1-я половина 2 в. до н.э.). Родился в Перге (Малая Азия). Основной его труд «Конические сечения» сохранился не стопроцентно (1-ые четыре книжки) в оригинале, отчасти (три следующие книжки) в арабском переводе, восьмая книжка утеряна. Исследуя характеристики конических сечений, их поперечников, фокусов, нормалей и касательных, воспользовался проективно-геометрическими способами.

5
Радиальным именуется такое преобразованием огромного количества aÈ{¥} (a — плоскость и ¥ — нескончаемо удаленная точка), при котором любая обобщенная окружность (т.е. окружность либо ровная плоскости a) отображается на обобщенную окружность. Инверсия — личный вариант радиального преобразования.

6
Л. Эйлер (1707-1783), математик, механик, физик и астролог. Родился в Базеле. С 1726 по 1741 и с 1766 являлся академиком Петербургской АН. Перечень трудов Эйлера содержит наиболее 850 заглавий. Главные работы относятся к вариационному исчислению, интегрированию обычных дифференциальных уравнений, степенным рядам, дифференциальной геометрии, теории чисел, небесной механике, оптике, гидродинамике. В конце 1766 года практически стопроцентно растерял зрение, но, продолжая активно работать, за 17 лет подготовил около 400 научных работ.

7
в случае, если треугольник ABC является тупоугольным.

]]>