Учебная работа. Дипломная работа: Содержание и значение математической символики

Учебная работа. Дипломная работа: Содержание и значение математической символики

Курсовая работа

Выполнила студентка факультета арифметики 4 курс 4 группа Клочанова Ольга Михайловна

Русский муниципальный педагогический институт им. А.И. Герцена

Санкт-Петербург

2002

Введение.

История науки указывает, что логическая структура и рост каждой математической теории, начиная с определенного шага ее развития, стают все в огромную зависимость от использования математической символики и ее усовершенствования.

Когда индийцы в V веке н. э. ввели символ нуля, они смогли бросить поразрядную систему счисления и развить абсолютную позиционную десятичную систему счисления, приемущество которой при счете если и не понимают, то ежедневно употребляют сотки миллионов людей. Алгебра и аналитическая геометрия должны почти всем тому, что Виет и Декарт разработали базы алгебраического исчисления. Введенные Лейбницем обозначения производной и интеграла посодействовали развить дифференциальное и интегральное исчисление; задачки на вычисление площадей, размеров, работы силы и т. п., решение которых ранее было доступно лишь высококлассным математикам, стали решаться практически автоматом. Благодаря этому обозначения Лейбница получили обширное распространение и просочились во все разделы науки, где употребляется математический анализ.

Пример с обозначением производной и интеграла в особенности ярко подтверждает корректность замечания Л. Карно, что в арифметике «знаки не являются лишь записью мысли, средством ее изображения и закрепления, – нет, они действуют на самую идея, они, до известной степени, направляют ее, и бывает довольно переместить их на бумаге, согласно известным весьма обычным правилам, для того, чтоб безошибочно добиться новейших истин».

В чем заключено беспристрастное содержание математической символики? Чем разъясняется

Математические знаки служат сначала для четкой (совершенно точно определенной) записи математических понятий и предложений. Их совокупа – в настоящих критериях их внедрения математиками – составляет то, что именуется математическим языком.

Внедрение символов дозволяет формулировать законы алгебры, также и остальных математических теорий в общем виде. Примером могут послужить формулы той же алгебры: (a+b)2
= a2
+ 2ab + b2

х1,2
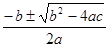=и т.п.

Математические знаки разрешают записывать в малогабаритной и легкообозримой форме предложения, выражение которых на обыкновенном языке было бы очень массивным. Это содействует наиболее глубочайшему пониманию их содержания, упрощает его сказать, что любой из их обозначает. В неприятном случае его могут не осознать.

В связи со произнесенным нужно выделить последующее. Арифметики не постоянно могут сказать сходу, что отражает тот либо другой знак, введенный ими для развития какой-нибудь математической теории, средствами которой можно решать фактически принципиальные задачки. Сотки лет арифметики оперировали отрицательными и всеохватывающими числами и получали с помощью их высококлассные результаты. Но беспристрастный смысл этих чисел и действий с ними удалось раскрыть только в конце XVIII и сначала XIX века. Лейбниц ввел знаки dx и dy, развил дифференциальное исчисление и при помощи правил крайнего показал исключительную оперативную силу этих знаков. Но Лейбниц не выявил беспристрастного смысла символов dx и dy; это сделали арифметики XIX века.

Знаки и системы символов играют в арифметике роль, очень схожую с той, какая в наиболее широких сферах зания и практической деятель людей принадлежит обыкновенному разговорному языку. Подобно обыкновенному языку, язык математических символов дозволяет обмениваться установленными математическими правдами, налаживать контакт ученых в совместной научной работе.

Решающим, но, будет то, что язык математических символов без обыденного языка существовать не может. Обыденный (естественный) язык содержательнее языка математических символов; он нужен для построения и развития языка математических символов. Язык математических символов лишь вспомогательное средство, присоединяемое к обыкновенному языку и применяемое в арифметике и в областях, где используются ее способы.

Возможность использования языка символов в арифметике обоснована чертами предмета ее исследовательских работ – тем, что она изучает формы и дела объектов настоящего мира, в узнаваемых границах безразличные к их вещественному содержанию. Существенна при всем этом и специфичность математических доказательств. Математическое подтверждение состоит в построении цепи выражений, исходным звеном которой являются настоящие начальные предложения, конечным – доказываемое утверждение. Промежные звенья цепи получаются в конечном счете из исходного и соединяются с ним и конечным звеном при помощи законов логики и правил логического вывода. Если начальные утверждения записаны в символической форме, то подтверждение сводится к их «механическим» видоизменениям.

Необходимость, а в наше время и необходимость – использования языка символов в арифметике обоснована тем, что при его помощи можно не только лишь коротко и ясно записывать понятия и предложения математических теорий, да и развивать в их исчисления и методы – самое основное для разработки способов арифметики и ее приложений. Достигнуть этого с помощью обыденного языка если и может быть, то лишь в принципе, но не в практике.

Достаточная оперативность символики математической теории значительно зависит от полноты символики. Это требование заключается в том, что символика обязана содержать обозначения всех объектов, их отношений и связей, нужные для разработки алгоритмов теории, позволяющих решать любые задачки из классов однотипных задач, рассматриваемых в данной нам теории.

Оперирование математическими знаками есть идеализированный пространство либо быть может (приближенно либо буквально) реализовано в реальности. Лишь потому оперирование математическими знаками способно служить открытию новейших математических истин.

Решающей силой развития математической символики является не «вольная воля» математиков, а требования практики математических исследовательских работ. Конкретно настоящие математические исследования помогают математикам в конце концов узнать, какая система символов лучшим образом показывает структуру рассматриваемых количественных отношений, в силу что быть может действенным орудием их предстоящего исследования.

§1. Введение нуля и развитие позиционной десятичной системы счисления.

Интуитивное представление о числе, по-видимому, так же старо, как и само население земли, хотя с достоверностью проследить все ранешние этапы его развития в принципе нереально. До этого чем человек научился считать либо выдумал слова для обозначения чисел, он, непременно, обладал приятным, интуитивным представлением о числе, позволявшим ему различать 1-го человека и 2-ух людей либо 2-ух и почти всех людей.

Наименования чисел, выражающие очень абстрактные идеи, возникли, непременно, позднее, чем 1-ые грубые знаки для обозначения числа объектов в некой совокупы. В глубочайшей древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, при этом предполагалось, что меж пересчитываемыми элементами огромного количества и знаками числовой записи существует взаимно однозначное соответствие. Но для чтения таковых числовых записей наименования чисел конкретно не использовались. сейчас мы с первого взора распознаем совокупы из 2-ух, 3-х и 4 частей; несколько сложнее распознаются на взор наборы, состоящие из 5, 6 либо 7 частей. А за данной нам границей установить на глаз их число фактически уже нереально, и нужен анализ или в форме счета, или в определенном структурировании частей. Счет на бирках, по-видимому, был первым приемом, который употреблялся в схожих вариантах: засечки на бирках размещались определенными группами. Весьма обширно был всераспространен счет на пальцах, и полностью может быть, что наименования неких чисел берут свое начало конкретно от этого метода подсчета.

Принципиальная изюминка счета заключается в связи заглавий чисел с определенной схемой счета. к примеру, слово «20 три» – не попросту термин, значащий полностью определенную (по числу частей) группу объектов; это термин составной, значащий «дважды по 10 и три». тут ясно видна роль числа 10 как коллективной единицы либо основания; и вправду, почти все считают десятками, поэтому что, как отметил еще руках и на ногах.

Система счисления, которой мы в главном пользуемся сейчас, десятичная позиционная. Десятичная, потому что ее основание 10. Основанием позиционной системы счисления именуется возводимое в степень целое число, которое равно количеству цифр, применяемых для изображения чисел в данной системе счисления. Основание указывает также, во сколько раз меняется количественное значение числа при перемещении ее на соседнюю позицию. В позиционных системах счисления количественный эквивалент (

Десятичная система характеризуется тем, что в ней 10 единиц какого-нибудь разряда образуют единицу последующего старшего разряда. Иными словами, единицы разных разрядов представляют собой разные степени числа 10.

Десятичной позиционной предшествовали остальные, основанные на разных принципах, системы счисления. Так примером непозиционной системы (другими словами таковой системы, где количественный эквивалент каждой числа не зависит от ее положения (места, позиции) в записи числа) может служить нумерация, применяемая старыми греками. Эта система относится к числу алфавитных. Первыми восемью знаками греческого алфавита (с добавлением «архаичной» буковкы 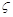=вау, имевшей =коппы, имевшей =сампи, означавшей 900, — сотки от 100 до 900, в конце концов, тыщи от 1000 до 9000 обозначались так же, как единицы, но со штрихом понизу: ,a означала 1000. Для того чтоб различать числа от слов, над ними ставилась черточка. Так, число 1305 греки записывали ,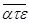. От греческой нумерации ведет свое происхождение древнерусская. Пример иной непозиционной системы дает употребляемая доныне римская нумерация.

Мы пользуемся ею для обозначения юбилейных дат, для нумерации неких страничек книжки (к примеру, страничек вступления), глав в книжках, строф в стихотворениях и т. д. В позднейшем собственном виде римские числа смотрятся так: I=1; V=5; X=10; L=50; С=100; D=500; M=1000.

О происхождении римских цифр достоверных сведений нет. Цифра V могла сначало служить изображением кисти руки, а цифра Х могла составиться из 2-ух пятерок. Буквально так же символ для 1000 мог составиться из удвоения знака для 500 (либо напротив).

Все целые числа (до 5000) записываются при помощи повторения вышеприведенных цифр. При всем этом если большая цифра стоит перед наименьшей, то они складываются, если же наименьшая стоит перед большей (в этом случае она не может повторяться), то наименьшая вычитается из большей. к примеру, VI=6, т.е. 5+1, IV=4, т.е. 5-1, XL=40, т е. 50-10, LX=60, т.е. 50+10. Попорядку одна и та же цифра ставится не наиболее 3-х раз: LXX=70; LXXX=80; число 90 записывается ХС (а не LXXXX).

1-ые 12 чисел записываются в римских цифрах так: I, II, III, IV, V, VI, VII, VIII. IX, X, XI, XII.

Примеры: XXVIII=28; ХХХIХ=39; CCCXCVII=397; MDCCCXVIII=1818.

Выполнение арифметических действий над неоднозначными числами в данной нам записи весьма тяжело. Тем не наименее римская нумерация преобладала в Италии до 13 века, а в остальных странах Западной Европы — до 16 века.

Античные египтяне употребляли десятичную непозиционную систему счисления. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, наименьших 10, необходимо было поставить соответственное число вертикальных штрихов. Чтоб записанные таковым образом числа было просто узнавать, вертикальные штришки время от времени объединялись в группы из 3-х либо 4 черт. Для обозначения числа 10, основания системы, египтяне заместо 10 вертикальных черт ввели новейший коллективный знак, напоминающий по своим очертаниям подкову либо крокетную дужку. Огромное количество из 10 подковообразных знаков, т.е. число 100, они поменяли остальным новеньким эмблемой, напоминающим силки; 10 силков, т.е. число 1000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили 10 лотосов согнутым пальцем, 10 согнутых пальцев – волнистой линией и 10 волнистых линий – фигурой ошеломленного человека. В итоге античные египтяне могли представлять числа до миллиона. Так, к примеру, при помощи коллективных знаков и повторений уже введенных знаков число 6789 в иероглифических обозначениях можно было бы записать как

Самые античные из дошедших до нас математических записей высечены на камне, но более принципиальные свидетельства древнеегипетской математической деятель запечатлены на еще наиболее хрупком и недолговечном материале – папирусе. Два таковых документа – папирус Ринда, либо египетского писца Ахмеса (ок. 1650 до н.э.) и столичный папирус, либо папирус Голенищева (ок. 1850 до н.э.) – служат для нас главными источниками сведений о древнеегипетских математике и геометрии. В этих папирусах наиболее древнее иероглифическое письмо уступило пространство скорописному иератическому письму, и это изменение сопровождалось внедрением новейшего принципа обозначения чисел. Группа схожих знаков заменялись наиболее обычный по начертанию пометой либо знаком, к примеру, девять записывалось как заместо , а семьсот как заместо . В данной нам записи число 6789 имело вид , при этом знаки наиболее высочайшего порядка размещались справа, а не слева.

Введение египтянами цифровых обозначений ознаменовало один из принципиальных шагов в развитии систем счисления, потому что отдало возможность значительно уменьшить записи.

Главные недочеты непозиционных систем нумерации — трудности с изображением произвольно огромных чисел и, основное, наиболее непростой, чем в позиционных системах, процесс вычислений. (Крайнее, правда, облегчалось употреблением счетных досок – абаков, так что изображение чисел было нужно только для конечного результата).

Большим шагом вперед, оказавшим грандиозное воздействие на все развитие арифметики было создание позиционных систем счисления. Первой таковой системой стала вавилонская шестидесятеричная система счисления, в какой возник символ , указывающий на отсутствие разряда, выполняющего роль нашего нуля. Концевой нуль, который дозволял различать, к примеру, обозначения для 1 и 60, у вавилонян отсутствовал. Удобство вычислений в шестидесятеричной системе сделало ее пользующейся популярностью у греческих астрологов. К. Птолемей (II в. н.э.) при вычислениях в шестидесятеричной системе пользуется знаком «0» для обозначения отсутствующих разрядов как посреди, так и в конце числа (0, омикрон – 1-ая буковка греческого слова ovden-ничто). О вавилонской шестидесятеричной системе нам припоминает деление часа на 60 минут и минутки на 60 секунд, также деление угла равного четырем прямым, на 360 градусов. Неудобство шестидесятеричной системы счисления в сопоставлении с десятичной – необходимость огромного количества символов для обозначения личных цифр (от 0 до 59), наиболее массивная таблица умножения.

Создание десятичной позиционной системы счисления, 1-го из выдающихся достижений средневековой науки, — награда индийских математиков. Позиционные десятичные записи чисел встречаются в Индии с VI в. Так, в дарственной записи 595 года встречается запись числа 346 цифрами брахми º(º-3, -4, -6). Первую достоверную запись нуля в виде кружочка мы находим в изображении числа 270 в стенной записи из Гвалиора, относящейся к 876г. время от времени ноль обозначался точкой. Непонятно, был ли нуль своим изобретением индийцев; может быть, они познакомились с ним по сочинениям александрийских астрологов.

Вот какова эволюция написания индийских цифр.

§2. Символика Виета и Декарта и развитие алгебры.

2.1 Развитие алгебры до Ф. Виета.

2.1.1 Алгебра греков.

Считается, что эллины заимствовали 1-ые сведения по геометрии у египтян, по алгебре — у вавилонян.

В древних египетских источниках папирусе Райнда и Столичном папирусе — находим задачки на «аха» (термин «аха» значит «куча», «груда»). Имеется в виду некое количество, неведомая величина, подлежащая определению) надлежащие современным линейным уравнениям, также квадратным вида ах2
= b. В вавилонских клинописных текстах имеется огромное число задач, решаемых при помощи уравнений и систем первой и 2-ой степеней, которые записаны без знаков, но в специфичной терминологии. В этих текстах решаются задачки, приводящие к трехчленным квадратным уравнениям вида ах2
— bх = с либо х2
— рх = q. В задачках на «аха» можно найти зачатки алгебры как науки о решении уравнений.

Но если вавилоняне за два тысячелетия до нашей эпохи умели числовым методом решать задачки, связанные с уравнениями первой и 2-ой степеней, то развитие алгебры в трудах Евклида (365 — ок. 300 гг. до н. э.), Архимеда (287-212 гг. до н. э.) и Аполлония (ок. 260-170 гг. до н. э.) носило совсем другой нрав: греки оперировали отрезками, площадями, размерами, а не числами. Их алгебра строилась на базе геометрии и выросла из заморочек геометрии. В XIX в. совокупа приемов старых получила заглавие геометрической алгебры.

В качестве примера геометрической алгебры греков разглядим решение уравнения х2
+ ax = b2
.

Древние арифметики решали эту задачку построением и строили разыскиваемый отрезок так, как показано на рисунке.

На данном отрезке АВ (равном a) строили прямоугольник AMсо сторонами (а + х) и x, равновеликий данному квадрату (b2
), таковым образом, чтоб лишная над прямоугольником AL (равная ах) площадь ВМ была квадратом, по площади равным х2
. Сторона этого квадрата и давала разыскиваемую величину х. Такое построение называли гиперболическим приложением площади.

Дальше, полагая задачку решенной, разделяли АВ напополам точкой С, на отрезке LM строили прямоугольник MG, равный прямоугольнику ЕС. Тогда прямоугольник AM будет разностью квадратов DF и LF. Эта разность и квадрат LF известны, потому по аксиоме Пифагора можно получить квадрат DF. Опосля этого находили величину DC(равную ½a +x) и DB (равную х).

Геометрическое построение в точности соответствует преобразованию, при помощи которого в современных обозначениях решается уравнение обозначенного типа:

b2
= ax + х2
= –

естественно же, при таковых построениях отыскивались лишь положительные корешки уравнений: отрицательные числа возникли в арифметике существенно позднее.

При помощи геометрии старым удавалось также обосновывать почти все алгебраические тождества. Но каковы эти подтверждения! Они идеальны в отношении логики и очень громоздки. Ах так определяет Евклид аксиому, выражающую тождество (а + b)2
= a2
+ 2аb +b2
. Если отрезок (ab) разбит в точке (g) на два отрезка, то квадрат, построенный на (ab), равен двум квадратам на отрезках (ag, gb) совместно с двойным прямоугольником на (ag, gb).

естественно, связывая число с геометрическим образом (линией, поверхностью, телом), античные оперировали лишь однородными величинами; так, равенство было может быть для величин схожего измерения.

Такое построение арифметики позволило древним ученым добиться существенных результатов в обосновании теорем и правил алгебры, но в предстоящем оно сделалось сковывать развитие науки.

Приведенные примеры могут сделать чувство, что математика старых греков примитивна. Но это не так: сделанная ими математика по собственному идеологическому содержанию глубока и питала мыслями и способами арифметику прямо до XVII в. — века научной революции; почти все идеи старых получили предстоящее развитие в новейшей арифметике, сделанной усилиями выдающихся разумов XVI—XVII вв.

Скопленные в странах Старого Востока познания состояли из набора разрозненных математических фактов, рецептур для решения неких определенных задач и не могли владеть достаточной строгостью и достоверностью. Создание основ арифметики в том виде, к которому мы привыкли при исследовании данной нам науки в школе, выпало на долю греков и относится к VI—V вв. до н. э. С этого времени начала развиваться дедуктивная математика, построенная на серьезных логических подтверждениях.

2.1.2 Алгебра Диофанта.

Новейший подъем древней арифметики относится к III в. н. э., он связан с творчеством величавого математика Диофанта. Диофант возродил и развил числовую алгебру вавилонян, освободив ее от геометрических построений, которыми воспользовались греки.

У Диофанта в первый раз возникает буквенная символика. Он ввел обозначения: неведомой z, квадрата d), куба c, четвертой dd (квадратоквадрат), пятой dc (квадратокуб) и 6-ой степеней ее, также первых 6 отрицательных степеней, т. е. разглядывал, величины, записываемые нами в виде x6
, x5
, x4
, x3
, x2
, x, x-1
, x-2
, x-3
, x-4
, x-5
, x-6
. Диофант использовал символ равенства (знак i) и символ для обозначения вычитания.

Диофант определил правила алгебраических опeраций со степенями неведомой, надлежащие нашим умножению и делению степеней с натуральными показателями (для m + n 6), и правила символов при умножении. Это отдало возможность компактно записывать многочлены, создавать умножение их, оперировать с уравнениями. Он указал также правила переноса отрицательных членов уравнения в другую часть его с оборотными заиками, обоюдного ликвидирования схожих членов в обеих частях уравнения.

«Математика» посвящена дилемме решения неопределенных уравнений. И хотя Диофант считает число собранием (а это значит, что рассматриваются лишь натуральные числа), при решении неопределенных уравнений он не ограничивается натуральными числами, а ищет и положительные оптимальные решения.

Неопределенными уравнениями до Диофанта занимались арифметики школы Пифагора в связи с пифагоровой аксиомой. Они находили тройки целых положительных чисел, удовлетворяющих уравнению x2
+ y2
= z2
.

Диофант поставил задачку установить разрешимость (в оптимальных числах) и в случае разрешимости отыскать оптимальные решения уравнения F (х, у) = 0, где левая часть – многочлен с целыми либо оптимальными коэффициентами. Он изучил неопределенные уравнения 2-ой, третьей и четвертой степеней и системы неопределенных уравнений.

Во 2-ой книжке «Математики» он так изучит, к примеру, уравнение второго порядка F (х, у) = 0.

Это уравнение задает коническое сечение. Всякому оптимальному решению уравнения соответствует точка кривой с оптимальными координатами. Пусть a, b– такие координаты, т. е. F (a, b) = 0.

Диофант делает подстановку у = b + k (х – а), либо y = b + kt, х = а + t.

ТогдаF (а + t, b + kt) = F (a, b) + tA (а, b) + ktB (а, b) + t2
C (a, b, k) = 0.

Но F (a, b) = 0, потому t = –.

Это значит, что любому оптимальному значению параметра k соответствует рациональное же

способы Диофанта потом применяли и развивали арабские ученые, Виет (1540—1603), Ферма, Эйлер (1707—1783), Якоби (1804—1851), Пуанкаре (1854—1912).

Оценивая творчество Диофанта, Цейтен отмечает существенную деталь: «В конце концов, мы хотим тут кратко указать на важную роль, сыгранную потом сочинениями Диофанта. Благодаря тому, что определенные уравнения первой и 2-ой степени были облечены у него в численную оболочку они оказались еще наиболее доступными для людей, не посвященных еще в культуру греческой арифметики; наиболее доступными, чем те абстрактные геометрические формы, которые принимают у Евклида уравнения 2-ой степени и которые мы встречаем в сохранившихся до нас трудах остальных геометров для выражения уравнений первых 2-ух степеней. Потому Диофант и явился основным посредником в процессе усвоения греческой алгебры арабами, благодаря которым, в свою очередь она просочилась в Европу в эру возрождения наук».

2.1.3 Алгебра индусов.

Начиная с V в. центр математической культуры переместился на восток — к индусам и арабам. Математика индусов резко различалась от арифметики греков она была числовой. Индусы не были озабочены строгостью эллинов в подтверждениях и обосновании геометрии. Они наслаждались чертежами, на которых у греков основывалось подтверждение, сопровождая их указанием: «Смотри!». Предполагается, что благодаря числовым выкладкам и практическому эмпиризму индусам удалось понять аксиомы и способы греков, теоретического обоснования которых они, может быть, по-настоящему не соображали.

Главные заслуги индусов заключаются в том, что они ввели в воззвание числа, именуемые нами арабскими, и позиционную систему записи чисел, нашли двойственность корней квадратного уравнения, двузначность квадратного корня и ввели отрицательные числа.

Индусы разглядывали числа безотносительно к геометрии. В этом их алгебра имеет сходство с алгеброй Диофанта. Они распространили правила деяния над оптимальными числами на числа иррациональные, производя над ними конкретные выкладки, а не прибегая к построениям, как это делали греки. к примеру, им было понятно, что

Греки, не знавшие отрицательных чисел, решая уравнения, преобразовывали их так, чтоб обе части уравнения при значении неведомой, удовлетворяющей этому уравнению, были положительными. Если этого не происходило, то изменялись условия задачки. Индусы в подобных ситуациях не были стеснены в собственных действиях: они или отбрасывали получающиеся отрицательные решения, или интерпретировали их как долг, задолженность. Отсюда изготовлен был естественный шаг к установлению правил действий над величинами при любом выборе символов этих величин, также к выявлению наличия 2-ух корней у квадратных уравнений и двузначности квадратного корня.

Индусами был изготовлен шаг вперед по сопоставлению с Диофантом и в совершенствовании алгебраической символики: они ввели обозначения нескольких разных неведомых и их степеней, которые были, как у Диофанта, на самом деле дела сокращениями слов. Не считая того, они находили решения неопределенных уравнений не в оптимальных, а в целых числах.

2.1.4 Алгебра арабов.

Предстоящее развитие математика получила у арабов, завоевавших в VII в. Переднюю Азию, Северную Африку и Испанию. Создались подходящие условия для слияния 2-ух культур – восточной и западной, для усвоения арабами обеспеченного математического наследства эллинов и индусской математики и алгебры.

Но еще до того как началось усиленное исследование арабами трудов старых математиков, в 820 г., вышел трактат по алгебре «Короткая книжка о исчислении ал-джабра и ал-мукабалы» Мухаммеда ибн Муса ал-Хорезми (т. е. из Хорезма, 787 – ок. 850г. н. э.), где давались числовое и геометрическое решения уравнений первой и 2-ой степеней.

Заглавие трактата соответствует операциям при решении уравнений: «ал-джабр» (восстанавливать) значит восстановление отрицательного члена в одной части уравнения в виде положительного в иной. к примеру, преобразовав уравнение

2х2
+ Зх -2 = 2х к виду 2х2
+ Зх = 2х + 2, мы произвели операцию ал-джабр.

«Ал-мукабала» значит сравнение схожих членов, приведение их к одному; в нашем уравнении подобные члены Зх и 2х, потому получим 2×2
+ x = 2.

Модификация слова ал-джабр породила наиболее позже алгебра. Аналогично, слово алгорифм (метод) вышло от ал-Хорезми.

Основное внимание в трактате ал-Хорезми направляет на решение уравнений вида

ax2
= bx, ax2
= c, ax2
+ bx = c, ax2
+ c = bx, bx + c = ax2
, bx = c,

которые определяет словесно, к примеру, так: «квадраты и корешки равны числу» (ах2
+ bх = с). Он высказывает правила, дающие лишь положительные решения уравнений, описывает условия, при которых эти решения есть. Обоснование правил ал-Хорезми дает в духе геометрической алгебры старых.

От арабов Европа получила последующий метод решения уравнения

х2
+ ах = b.

Построим квадрат х2
, к его сторонам приложим четырехугольники длины х + 2а/4 = х + а/2 и ширины а/4. Тогда площадь приобретенного квадрата = x2
+ ax + .

означает, x2
+ ax + = = b + , = b + .

Величины b и а известны, потому можно выстроить , откуда х + = —. Вообщем, ал-Хорезми, приведший в собственном сочинении этот способ, уравнению ах2
+ с = bх приписывал два корня.

В трактате приведены некие сведения о действиях над алгебраическими выражениями, примеры решения треугольников много задач о разделе наследия приводящих к уравнениям первой степени. Таковым образом, трактат ал-Хорезми не содержал ничего новейшего по сопоставлению с тем, что было у греческих создателей и индусов, но он заслуживает внимания поэтому, что в течение долгого времени был управлением, по которому велось обучение (педагогический процесс, в результате которого учащиеся под руководством учителя овладевают знаниями, умениями и навыками) в Европе.

2.1.5 Развитие алгебры в Европе.

Каково же было состояние арифметики в это время в Европе. О этом наука располагает очень скудными сведениями.

В XII – XIII вв. в Европе активно переводились в арабского языка как труды самих арабов, так и работы старых греков, переведенные на арабский язык.

Первым европейским математиком, которому удалось осветить почти все вопросцы и внести в арифметику собственный вклад, был Леонардо Пизанский (Фибоначчи, 1180–1240), написавший «Книжку абака». В ней рассмотрены разные задачки, указаны способы их решения, при этом математика и алгебра линейных и квадратных уравнений изложены с необычной ранее времени точностью и полнотой.

Существо задачки Леонардо излагает словесно; неведомую он именует res (вещь) либо radix (корень); квадрат неведомой – census (имущество) либо quadratus (квадрат); данное число – numerus. Все это латинские пероводы соответственных латинских слов.

Современник Леонардо, Иордан Неморарий (XIII в), употреблял буквенные обозначения наиболее систематично и решал задачки с применением линейных и квадратных уравнений, поначалу в общем виде, а потом иллюстрировал их числовыми примерами.

Французский епископ Николь Орем (1323-1382) разглядывал «дробно – оптимальные дела», соответствующе современным степеням a½
, a¼
, a3/2
и т.д., определил правила операций с этими отношениями типа , , , ,

Орем впритирку подошел к понятию иррационального показателя. Он обосновал расходимость гармонического ряда 1 + +++…

Выдающимся алгебраистом собственного времени стал монах-францисканец Лука Пачоли (ок. 1445 – ок.1514) близкий друг Леонардо да Винчи, работавший доктором Арифметики в институтах и разных учебных заведениях Рима, Болоньи, Неаполя, Флоренции, Милана и остальных городов.

Он ввел «алгебраические буковкы» (caratterialgebraici), отдал обозначения квадратному и кубическому корням, корню четвертой степени; неведомую х он обозначал со (cosa – вещь), х2
– се (censo — квадрат, от латинского census), х3
– cu (cubo), x4
– се. се. (censo de censo), x5
– р°г° (primo relato – «первоеrelato», x6
– р°г° х – се. cu. (censo de «второеrelato»), х8
– ce. ce. ce. (de censo), x9
– cu. cu. (cubo de cubo), x10
– ce. p°r° (censo de primo relato), x13
– 3°r° (tersio relato — «третье relato») ит. д.; свободныйчленуравнения– n° (numero – число). Как лицезреем, некие степени Пачоли получал мультипликативным методом при помощи характеристик 2 и 3 (х4
= х2
×2
, х6
= х2
×3
, х9
= х3
×3
и т. д.), а в вариантах, когда так не выходило, воспользовался словом relato (к примеру, при образовании х5
, х7
, х11
и т. д.). Особыми знаками Пачоли обозначил вторую неведомую и ее степени. Для обозначения операции сложения он пользовался знаком (plus – больше), для обозначения вычитания – знаком (minus – меньше). Он определил правила умножения чисел, перед которыми стоят знаки и .

Раздел «Суммы», посвященный алгебраическим уравнениям, Пачоли окончил замечанием о том, что для решения кубических уравнений х3
+ ах = b и х3
+ b = ах «искусство алгебры еще не отдало метода, как не дан еще метод квадратуры круга».

Некий шаг в совершенствовании алгебраической символики сделал бакалавр медицины Н. Шюке (мозг. ок. 1500 г.), который в книжке «Наука о числах в 3-х частях» выложил правила действий с оптимальными и иррациональными числами и теорию уравнений. Для сложения и вычитания он вослед за Пачоли воспользовался знаками и , при этом, символ служил и для обозначения отрицательного числа. Неведомую величину он называл premier («1-ое число»), а ее степени – вторыми, третьими и т. д, числами. Записи степеней неведомой у Шюке лаконичны. к примеру, современные знаки 5, 5ж, 5х, 5х2
, 5х3
у него выглядели бы так: 5°, 51
, 52
, 53
. Заместо равенства 8х3
×7х-1
= 56х2
Шюке писал: «83
, умноженное на 71
×
, дает 562
». Таковым образом, он разглядывал и отрицательные характеристики. Относительно вольных членов уравнения Шюке указывал, что эти числа «имеют имя нуль».

Значимого фуррора в совершенствовании «алгебраических букв» Луки Пачоли достигнули германские алгебраисты – «коссисты». Они заместо и ввели знаки + и –, знаки для неведомой, и ее степеней, вольного члена.

XVI в. в алгебре ознаменовался величайшим открытием – решением в общем виде уравнений третьей и четвертой степеней.

Спицион дель Ферро в 1506 г. отыскал решение кубического уравнения вида

x3
+ ax = ba,b >0. (1)

Чуток позднее Тарталья указал решение этого же уравнения в виде х = — , где u – v = b, uv = , откуда u и v находятся как корешки квадратного уравнения.

Также он отыскал решение уравнения x3
= ax + ba,b >0 (2)

в виде х = + , где u + v = b, uv = .

Уравнение же x3
+ b = axa,b >0 можно решить при помощи уравнения (2).

В те времена предпочитали избегать отрицательных корней и задачки, сводящиеся к отрицательным корням уравнения (2), преобразовывали так, чтоб они приводили к положительным корням уравнения (3). Только Кардано позднее понял выгоду рассмотрения отрицательных корней.

Почему рассматривались лишь уравнения вида (1) и (2)? На этот вопросец ответ отдал Кардано.

Чтоб разобраться в нем, разглядим полное уравнение третьей степени.

y3
+ ay2
+ by + c = 0.

Не следует мыслить, что Тарталья и Кардано писали такие уравнения. Нет, так стали поступать еще позднее. Записывать все члены уравнения в одной части, приравнивая к одной части, начал Декарт. Ну и символики не было, воспользовались прообразами знаков и словами. Уравнение x3
+ ax = b записывалось приблизительно так: «куб» (х3
) некое количество (а) «вещей» (х) равно данному «числу» (b). Осознать можно, но оперировать трудно.

Полное уравнение можно конвертировать в неполное, не содержащее члена с квадратом неведомой. Создадим подмену y = x + a и подставим в уравнение; получим х3
+ (3a + а)х2
+ (3a2
+ 2aа + b)x + (a3
+ aa2
+ ba + c) = 0.

Положим 3a + а = 0. Найдем отсюда a = — а/3 и подставим в выражения

p = 3a2
+ 2aа + b, q = a3
+ аa2
+ ba + c.

Тогда уравнение воспримет вид х3
+ px + q = 0.

В нашей символике это уравнение соответствует уравнениям (1), (2), которые решал Тарталья.

Кардано вызнал метод решения уравнений третьей степени, предложенный Тартальи, опубликовал его. Формула же стала носить заглавие «формулы Кардано».

Выведем сейчас ее.

Разглядим уравнение х3
+ px+ q = 0. Введем новейшие неведомые x = u + v и подставим их в начальное уравнение; получим u3
+ v3
+ (3uv + p)(u + v) + q = 0.

Приравняем 3uv + p к нулю: 3uv + p = 0.

Уравнение воспримет вид u3
+ v3
+ q = 0. Тогда uv = – , u3
v3
= – , u3
+ v3
= -q.

Выражения u3
и v3
можно принять за корешки квадратного уравнения z2
+ qz – = 0.

Решая его, получим z1
= – + , z2
= – – .

Таковым образом, x = u + v = +, x =+.

Это и есть формула Кардано. Не излишне увидеть, что в таком виде Кардано ее не находил: он формулировал решение уравнений (1) и (2) и разглядывал связь меж уравнениями (2) и (3).

В случае, когда +<0, под квадратным корнем выходит отрицательное число и корень дает мнимость. Этот вариант получил заглавие неприводимого, потому что решение уравнения третьей степени не приводится к решению квадратного уравнения. Как уже говорилось, с ним не совладали ни Тарталья, ни Кардано. Его при помощи тригонометрии разобрал Виет.

Чтоб получить записывалось так Rx
.u.cu.Rx
.10810½Rx
.u.cu.Rx
.10810.

тут Rx
– символ корня (Radix), Rx
.u.cu значит корень кубический из всего выражения до вертикальной черты либо опосля нее, и — сокращения слов plus и minus.

Кардано показал, что просто можно решить уравнение x4
ax = bx2
+ . Он привел его к виду x4
= b(x)2
, а потом извлечением корня получил квадратное уравнение. Аналогично он разглядывал и некие остальные виды уравнений.

Но уравнение x4
+ 6×2
+ 36 = 60x, предложенное да Которые Кардано не смог решить.

Открыл способ решения уравнений четвертой степени 23 – летний ученик Кардано – Луиджи Ferrari.

Опосля того, как были изучены уравнения третьей степени, задачка о уравнениях четвертой степени стала наиболее легкой. Ferrari разглядывал уравнение, не содержащее члена с x3
, т.е. уравнение вида x4
+ ax2
+ bx + c = 0.

Он преобразовывал его так, чтоб в левой части был полный квадрат, а в правой – выражение не выше 2-ой степени относительно x.

Выделением полного квадрата выходило = x4
+ ax += -bx – c + , = -bx – c + .

сейчас следовало выполнить такие преобразования, чтоб из левой и правой частей можно было извлечь корень. С данной нам целью Ferrari вводил новейшую переменную t и добавлял к обеим частям выражение 2t + t2
. Этодает= 2tx2
– bx – c + at + + t2
, = 2tx2
– bx + (– c + + at + t2
).

необходимо, чтоб правая часть была полным квадратом. Вспомним, как обстоит дело с трехчленом ax2
+ bx + c. Выделим в нем полный квадрат: ax2
+ bx + c = а(x2
+ x + ) = =a(x2
+ 2x× + — +) = a(x2
+ 2x× + + ) = a(x+)2
+ .

Трехчлен будет полным квадратом, когда 4ac – b2
= 0. В нашем случае роль коэффициента при x2
играет 2t, а роль вольного члена — выражение в скобках правой части уравнения. Тогда выражению 4ac – b2
= 0 соответствует 4×2t(t2
+ at + — c) – b2
= 0, b2
= 2t(4t2
+ 4at + a2
— 4c).

Таковым образом, нахождение t свелось к решению кубического уравнения, а x находится з квадратного уравнения опосля извлечения корня из левой и правой частей, т.е. из уравнения x2
+ + t0
= .

Кардано отмечает, что таковым же приемом можно решать уравнения, в каких отсутствует член не с третьей степенью х, а с первой. В этом случае делается подстановка х = k/y.

Открытия, изготовленные итальянцами в алгебре и систематически изложенные Кардано, стали доступны математикам остальных государств и дали импульс развитию науки.

Предстоящее развитие алгебры было соединено с совершенствованием символики и разработкой общих способов решения уравнений.

В этом преуспел Франсуа Виета.

2.2 Символика Виета и развитие алгебры.

Виет считается одним из основателей алгебры. Но его Энтузиазм к алгебре сначало связан с вероятными приложениями к тригонометрии и геометрии. А задачки тригонометрии и геометрии, в свою очередь, приводили Виета к принципиальным алгебраическим обобщениям. Так было, к примеру, с решением уравнений третьей степени в неприводимом случае и с исследованием неких классов разрешимых алгебраических уравнений высших степеней.

Свою алгебру Виет ценил весьма высоко. Он не воспользовался словом «алгебра», эту науку он зазывал «искусством анализа». Виет различал видовую логистику и числовую логистику. термин «логистика» значит совокупа арифметических приемов вычислений, «вид» имел смысл знака.

Видовая логистика Виета опосля внесенных им в символику усовершенствований представляла собой буквенное исчисление. Ее объектами служат геометрические и псевдогеометрические образы, связанные меж собой разными соотношениями. Виет был последователем старых: он оперировал таковыми величинами, как сторона, квадрат, куб, квадратоквадрат, квадратокуб , и т. д., образующими своеобразную лестницу скаляров. Деяния над скалярами у Виета, как и у старых геометров, подчинены «закону однородности»: составленные из неведомых и узнаваемых величин уравнения должны быть однородными относительно всех их совместно взятых. Умножению чисел у Виета соответствует образование новейшего скаляра, размерность которого равна сумме размерностей множителей. Операция, соответственная делению чисел, дает новейшую величину, размерность которой равна разности размерностей.

Виет разработал символику, в какой вровень с обозначением неведомых в первый раз возникли знаки для случайных величин, именуемых в истинное время параметрами. Для обозначения скаляров он предложил воспользоваться строчными знаками: «разыскиваемые величины будут обозначены буковкой А либо иной гласной Е, I, О, U, Y, а данные – знаками B, D, G либо иными согласными»

слово «коэффициент» введено Виетом. Рассматривая выражение

(А + В)2
+ D(A + В),

он именовал величину D, участвующую с А + В в образовании площади, longitudeciefficiens, т. е. способствующей длиной.

Из символов Виет употреблял +, — и дробную черту. Современные скобки у него подменяла общая черта на всем выражением.

Символика Виета мачалась недочетами, в неких отношениях она была наименее совершенна, чем у его предшественников и современников. Виет для записи действий употреблял слова: in у него означало умножение, aequatur подменяло символ равенства. Словами же выражались степени разных величин. Для 3-х низших степеней он брал наименования из геометрии, к примеру, А3
называл Acubus. Высшим степеням он давал геометрические наименования, происходящие от низших: А9
, к примеру,— Acubo-cubo-cubus. Популярная величина В представлялась как величина девятой степени записью solido-solido-solidum. Если сторона (latus) множится на неведомую величину, то она именуется способствующей) (coefficiens) при образовании площади.

Уравнение А3
+ 3ВА = DВиет записывал так: А cubus + В planumin 43aequaturDsolido, а уравнение ВАn
–Аm+
n
= Z так:

В parabolain Аgradum — АpotestateaequaturZhomogenae (В, умноженное на градус А, минус А в степени приравнивается однородной Z),

Обозначения в числовой логистике выглядели проще:

N – 1-ая степень, Q – квадрат, С – куб и т. д. Уравнение x3
— 3x = 1 записывалось в виде 1С – 3Naequatur 1»

Неудобства символики Виета соединены и с требованием однородности. Как и античные греки, Виет считал, что сторону можно ложить лишь со стороной, квадрат – с квадратом, куб – с кубом и т. д. В связи с сиим появлялся легитимный вопросец: имеют ли Право на существование уравнения выше третьей степени, так как в пространственном мире 4-ая, 5-ая и т. д. степени аналогов не имеют.

Для придания уравнению однородности Виет опосля входящих в него характеристик писал planum (плоскость), solidum (тело) и т. д. Ах так смотрится в записи Виета уравнение х3
+ ЗВ2
х = 2z3
: Acubus + В plano 3 inAaequariZsolido 2.

правило Тартальи для решения уравнения третьей степени у Виета имело вид:

.

Символики Виета придерживался потом П. Ферма. От «деспотии» однородности просто и остроумно смог освободиться Декарт (о этом будет сказано далее).

Может показаться, что Виет ввел в символику алгебры совершенно мало. Знаками для обозначения отрезков воспользовались еще Евклид и Архимед, их удачно применяли Леонардо Пизанский, Иордан Неморарий, Николай Орем, Лука Пачоли, Кардано, Бомбелли и почти все остальные арифметики. Но сделал значимый шаг вперед Виет. Его символика дозволила не только лишь решать определенные задачки, да и отыскивать общие закономерности и стопроцентно доказывать их. Это, в свою очередь, содействовало выделению алгебры в самостоятельную ветвь арифметики, не зависящую от геометрии. «Это нововведение (обозначение знаками данных и разыскиваемых) и в особенности применение буквенных коэффициентов положило начало коренному перелому в развитии алгебры: лишь сейчас сделалось вероятным алгебраическое исчисление как система формул, как оперативный метод».

Произнесенное, просто подтвердить примерами. Пусть х1
, x2
– корешки квадратного уравнения. Перемножим разности x – x1
и х – х2
: (x – x1
)(х – х2
)=х2
– (х1
+ х2
)х + х1
х2
.

Обозначим (x – x1
)(х – х2
) = х2
+ px + q, сравнивая с предшествующим, получим p = – (х1
+ х2
), q = x1
x2
.

Выполним то же самое для кубического уравнения:

(x – x1
)(х – х2
)(x – x3
)=x3
– (х1
+ х2
+ x3
)x2
+ (x1
x2
+ x1
x3
+ x2
x3
)x – x1
x2
x3
.

Сравним итог с выражением (x – x1
)(х – х2
)(x – x3
) = x3
+ a1
x2
+ a2
x + a3
.

Это дает a1
= – (x1
+ x2
+ x3
)

a2
= x1
x2
+ x1
x3
+ x2
x3

a3
= – x1
x2
x3
.

Таковой итог для квадратного уравнения был известен Кардано (в случае положительных корней – к тому же ранее); Кардано отметил свойство корней кубического уравнения относительно коэффициента при х2
. Но никакого обоснования в общем виде отдать он не мог; это сделал Виет для уравнений до пятой степени включительно.

Достоинства символики предоставили Виету возможность не только лишь получить новейшие результаты, да и наиболее много и обоснованно выложить все известное ранее. И если предшественники Виета высказывали некие правила, рецептуры для решений определенных задач и иллюстрировали их примерами, то Виет отдал полное изложение вопросцев, связанных с решением уравнений первых 4 степеней.

Разглядим ход рассуждений Виета при решении кубического уравнения.

Возьмем уравнение x3
+ 3ax = 2b. Положим a = t2
+ xt.

Найдем отсюда

х = и подставим в начальное уравнение. Получим + 3a = 2b, откуда для определения t наводим квадратное уравнение относительно t3
: (t3
)2
+ 2bt3
– а3
== 0.

Отсюда обусловится t, а потом и х. Заметим еще, что подстановка а = t2
+ xt приводит начальное уравнение к виду

(х + t)3
– t3
= 2b,

которое совместно с уравнением (х + t)t = a, (х + t)3
t3
= a3
отдало бы возможность применить способ Тартальи и дель Ферро. Но Виет таковым методом не начал двигаться.

Разглядим сейчас пример. Найдем способом Виета действительный корень уравнения

х3
+ 24x=56.

тут а=8, b=28. Запишем уравнение относительно t: (t3
)2
+ 56t3
— 83
— 0.

Решим его:

t3
= –28 = – 2836 t1
= = 2 t2
= = –4.

Найдем сейчас х:

x1
= = –2 , x2
= = 2 = x1
.

При изложении способа Ferrari для решения уравнения четвертой степени Виет провел аналитически выкладки, обозначенные выше, и получил уравнение, содержащее основную неведомую А и вспомогательную Е (х и t у Ferrari).

Виет, верный последователь старых, оперировал лишь оптимальными положительными числами, которые он обозначал знаками. Если в итоге подстановки в уравнение значений характеристик неведомое оказывалось иррациональным, он давал этому случаю особенное обоснование.

В качестве примера такового обоснования приведем «геометрическое» решение кубического уравнения по способу дель Ферро – Тартальи.

В записи Виета уравнение имело вид A3
+ 3BA = D.

Известное решение: А является разностью «сторон» которые образуют площадь В и разность кубов которых равна D. Если обозначить «стороны» знаками u и v, то uv = B,u3
– u3
=D, A=u–v.

Виет присваивал решению «геометрическое» истолкование; он заместо Dsolidum записывал произведение В planum на D, т. е. получал уравнение A3
+ 3ВA=BD.

Потом он определял четыре величины, образующие «геометрический ряд», так, чтоб прямоугольник, построенный на средних либо на последних, по площади приравнивался В, а разность последних была D. Тогда A будет разностью средних.

Поясним произнесенное. Обозначим эти четыре величины через z,u, v и t. Тогда можно записать

z:u = u:v = v:t, zt = uv = B, z – t = D, A = u – v.

Если в решении Тартальи D поменять на BD, то оба решения совпадут.

метод Виета значит подмену кубического корня 2-мя средними геометрическими, что стопроцентно соответствует духу старых греков.

Из получившихся пропорций найдем

u3
= z2
t, v3
= ztu3
– v3
= zt(z – t) = BD

Виет особо разглядывал трехчленные уравнения разных степеней и сначала интересовался количеством их корней, имея в виду лишь положительные корешки. Отрицательные корешки он определял как корешки уравнения, в каком неведомое х заменено на –у. Виет , получал трехчленные уравнения из квадратных; он поступал так, чтоб число положительных корней оставалось прежним. При всем этом он воспользовался подстановкой х = kym
либо особыми приемами.

один из приемов Виета смотрится так. Пусть дано уравнение

x2
+ ах = b, а, b>0.

Для получения уравнения четвертой степени возведем левую и правую части уравнения в квадрат:

(х2
+ах — b)3
= x4
+ a2
x2
+ b2
+ 2ax3
– 2bx2
– 2abx = 0

Приобретенное уравнение можно переписать:

x4
+ 2ах3
+ 2а2
x2
– а2
x2
+b2
– 2bх2
– 2abx = 0.

Исключим 2ах3
+ 2a2
x2
, воспользовавшись тем, что b= х2
+ ax:

2ах(х2
+ аx) = b2аx, 2ах3
+ 2a2
x = 2abx.

Тогда x4
+ 2abx – а2
x2
+b2
– 2bx2
– 2abx = 0, x4
–a2
x2
+b2
– 2bx2
= 0.

сейчас осталось исключить x2
; из начального уравнения найдем: x2
= b – ax и подставим в крайнее:

x4
– (a2
+ 2b)x2
+ b2
= 0, x4
– (a2
+ 2b)(b – ax) + b2
= 0, x4
+ (2ab + a3
)x = b2
+ a2
b

Приобретенное уравнение четвертой степени имеет те и лишь те положительные корешки, которые были у начального квадратного.

Для нахождения трехчленного уравнения третьей степени Виет в качестве начального брал уравнение

ax– x2
= ab

и множил его левую и правую части на х + b; это при водило к уравнению

(а – b)х2
– х3
= ab2

с теми же положительными корнями, которые были у квадратного.

И еще один личный вопросец разглядел Виет. В уравнении

ахm
– xm
+
n
= b

имеющем по условию два корня, он обусловил коэффициенты, при которых корешки уравнения имели бы данные значения.

Пусть эти корешки у и z. Тогда

a =, b =

Ту же задачку он решил относительно уравнения

xm
+
n
+ axm
=b, где m + n – число четное, m – нечетное.

Очень принципиально то, что Виет распространил известные ранее личные преобразования на все алгебраические уравнения. Подстановку х = у + k, применявшуюся Кардано для исключения из кубического уравнения члена 2-ой степени, он применил к уравнениям хоть какой степени. Также известную Кардано оборотную подстановку х = k/y Виет употреблял, чтоб освободиться в неких вариантах от отрицательных коэффициентов и иррациональностей. к примеру, уравнение х4
– 8х = подстановкой х = он преобразовал к виду y4
+ 8у3
= 80. Подстановкой х = y Виет преобразовывал уравнение n-й степени так, что коэффициент при члене (n -1)-й степени (a) становился равным b, в то время как старший коэффициент оставался равным единице. Подстановку х = ky он использовал, чтоб избавиться от дробных коэффициентов.

Особенный Энтузиазм представляет исследование Виета по составлению уравнений из линейных множителей и по установлению связей меж корнями уравнения и его коэффициентами. Начальные сведения и по тому, и по другому вопросцу были у Кардано.

Кардано в ту пору, когда еще не знал способа дель Ферро и Тартальи, решал некие уравнения третьей степени разложением на множители. В уравнении

2х3
+ 4×2
+ 25 =l6x + 55

с данной нам целью он добавлял к обеим частям 2×2
+ 10x + 5. Потом преобразовывал его к виду (2х + 6)(х2
+ 5) = (х + 10)(2х + 6), сокращал на 2х + 6 и получал квадратное уравнение.

Кардано же при нахождении положительного корня уравнения х3
+ b= ах складывал егопочленно с уравнением у3
= ay + b, получал из их квадратное уравнение делением на х минус узнаваемый отрицательный корень х – (–у). Такое преобразование позволило Кардано установить, что коэффициент при члене 2-ой степени в правой части кубического уравнения равен сумме его корней. Это был 1-ый шаг к установлению зависимости меж корнями и коэффициентами алгебраического уравнения.

Виет составил полные уравнения с данными положительными корнями прямо до пятой степени и показал, как образуются коэффициенты при xn
-1
, xn
-2
, xn
-3
, … Он установил, что эти коэффициенты при условии, что старший коэффициент равен 1 либо –1 (вольный член в правой части был должен стоять со знаком +), представляют собой взятые с чередующимися знаками суммы: самих корней, парных произведений их, произведений корней, взятых по три, и т. д. Работа, в какой Виет тщательно разглядел это утверждение, до нас не дошла. Непонятно, как он поступал в том случае, когда уравнение имеет и отрицательные корешки. Но, быстрее всего, это не представляло для Виета особенных проблем: довольно было создать в уравнении подмену х = –у и можно оперировать с положительными корнями новейшего уравнения. Такие примеры в его работах встречались. Если уравнение х3
+ q = рх имеет два положительных корня х1
и х2
, то уравнение y3
= ру + q– один положительный корень у1
= –х3
при этом у1
= х1
+ х2
(это знал Кардано), x1
2
+ x2
2
+ x1
x2
= p, x1
x2
(x1
+ x2
) = q.

Как лицезреем, в исследовательских работах Виета встречались начала теории симметрических функций и разложения многочленов на линейные множители, что скоро привело к открытию главный аксиомы алгебры о числе корней уравнения случайной степени. Эти исследования Виета продолжили арифметики последующего поколения Т. Гарриот (1560— 1621), А.Жирар (1595-1632), Р. Декарт (1596-1650).

2.3 Символика Декарта и развитие алгебры.

В сочинении «Исчисление г. Декарта» неведомый создатель выложил арифметические базы арифметики Декарта. Они писал: «Эта новенькая математика состоит из букв a, b, c и т.д., также из цифр 1, 2, 3 и т.д. Если числа стоят перед знаками, к примеру, 2а, 3b, 1/4с, то это значит, что величина а берется двойной, величина b – тройной, а от величины с берется четверть. Но если они находятся сзади букв, к примеру, а3
, b4
, c5
, то это значит, что величина а множится сама на себя трижды, величина b– четыре раза, а величина с – 5 раз». «Сложение делается при помощи такового знака +. Так, чтоб сложить а и b, я пишу а + b. Вычитание делается при помощи такового знака –. Так, чтоб отнять а из b, я пишу b– a и т. д. Если в вычитаемом выражении есть несколько частей, то у их в нем меняются только знаки. Так, если из d требуется отнять а – b + с, то остается d – а + b– –с. Буквально так же при вычитании а2
– b2
из с2
– d2
остается с2
– d2
– а2
+ b2
. Но если имеются присоединенные числа и члены схожего вида, то их следует подписывать друг под другом и создавать их сложение и вычитание как в обычной математике… Если требуется помножить одну буковку на другую, то их следует только соединить совместно, но если имеются присоединенные, числа, то они следуют законам обычной математики. Что касается символов, то понятно, что + на + дает в произведении + и что –, умноженный на –, также дает в произведении +. Но + на – либо же –, умноженный на +, дает в произведении –».

Буквально так же определялись действие деления, операции с дробями «по правилам обычной математики». Вот рассуждение о корне: «Когда корень извлечь из квадрата недозволено, его квадрат помещают под связку , чтоб отметить, что его следует разглядывать как корень, тогда и его корень именуют иррациональной величиной».

Из всего этого видно, как далековато зашла формализация алгебраических действий по сопоставлению с тем, что было у старых греков и у предшественников Декарта; видно также, что надобности в геометрической интерпретации алгебры уже нет.

Формализации алгебры (и всей арифметики) очень содействовало то, что Декарт усовершенствовал буквенную символику. Он обозначал известные величины знаками а, b, с, . . ., неведомые («неопределенные») – знаками x, y, z, …. Он ввел обозначения степеней: a2
, a3
, х3
, . . . правда, квадраты величин он выражал и при помощи знаков аа, хх. Обозначение корня несколько различается от современного. Так, выражение значит один из кубических корней, входящих в формулу Кардано.

Все буковкы в формулах Декарта числились положительными величинами; для обозначения отрицательных величин ставился символ минус; если символ коэффициента произволен, перед ним ставилось многоточие. символ равенства имел необыкновенный вид . Ах так, к примеру, смотрелось уравнение с случайными коэффициентами:

+x4
…px3
…qx… 0.

И еще один знак использовал Декарт: он ставил звездочки, чтоб показать отсутствующие члены уравнения, к примеру:

x5
*** – b 0.

Остальные арифметики тех пор тоже воспользовались символикой, близкой к разработанной Декартом, а античные греки излагали свои мысли совершенно без символики. Ферма выстроил аналитическую геометрию, располагая припасом употребляемых до него алгебраических средств. «…все это может побудить нас недооценить те успехи, которые поставлены тут во главу всей математической деятель Декарта. внимание, как нередко мы должны были для изложения мыслях наиболее ранешних создателей прибегать к использованию алгебраической формой Декарта; без нее мы навряд ли смогли бы это создать сколь-нибудь сжато и наглядно. Мы смогли пользоваться данной нам алгебраической формой, с одной стороны, поэтому что декартова трактовка алгебры благодаря своим преимуществам получила сейчас обширное распространение, и знакомство с ней происходит уже в школе. С иной стороны, она уже сама по для себя в большенный мере расчистила путь многому, что ранее могло быть изложено только очень массивным образом и было потому доступно только весьма способным математикам» (Цейтен Г. Г, История арифметики в XVI и XVII веках, с. 202)

Другими словами, разработка и введение алгебраической символики сделали арифметику наиболее демократичной.

Уравнения, по утверждению Декарта, представляют собой равные друг другу суммы узнаваемых и неведомых членов либо же, если разглядывать эти суммы совместно, равны «ничему» (нулю). Декарт указал, что «уравнения нередко комфортно разглядывать конкретно крайним образом», т. е. в виде Р (х) = 0. Для теоретических построений Декарта таковая запись уравнений игралась важную роль.

Данной нам формой он воспользовался при установлении числа корней алгебраического уравнения, что привело к формулировке главный аксиомы алгебры: число корней уравнения (положительных — «настоящих», отрицательных — «неверных» и надуманных — «воображаемых») равно числу единиц в наивысшем показателе степени входящей в уравнение неведомой величины. Справедливость аксиомы он аргументировал тем, что при перемножении n биномов вида х – а выходит многочлен степени n. Недостающие «воображаемые» корешки, природу которых Декарт не объясняет, можно примыслить.

Если все корешки положительны, то, по словам Декарта, дело обстоит так: «Знайте, что всякое уравнение может иметь столько же разных корней либо же значений неведомой величины, сколько крайняя имеет измерений; ибо если, к примеру, принять х равным 2, либо же х – 2 равным ничему, также х = 3 либо же х – 3 = 0, то, перемножив оба эти уравнения x – 2 = 0 и x – 3 = 0, мы получим хх – 5х + 6 = 0, либо же хх = 5x – 6, уравнение, в каком величина х имеет

Если принять еще, что х – 4 = 0 и помножить это выражение на хх – 5x + 6 = 0, то мы получим х3
– 9хх + 2бх – 24 = 0, другое уравнение, в каком х, владея 3-мя измерениями, имеет совместно с тем три значения, а конкретно 2, 3 и 4»

Если же «х выражает собой также недочет какой-либо величины, скажем 5, то мы получим х + 5 = 0». Умножив х + 5 на левую часть предшествующего уравнения и приравняв итог нулю, получим

x4
– 4×3
– 19xx + 10бх – 120 = 0, (1)

«уравнение, у которого четыре корня, конкретно три настоящих 2, 3, 4 и один неверный –5».

Построение левой части уравнения в виде произведения биномов приводит к тому, что степень уравнения можно снизить, разделив левую часть его на х – a, где а – корень уравнения. С иной стороны, если такое деление нереально, то число а не будет корнем уравнения. Левую часть уравнения (1), к примеру, можно поделить на х – 2, х – 3, х – 4, х + 5 и недозволено поделить на хоть какой иной бином х – а; «это указывает, что оно может иметь только четыре корня: 2, 3, 4 и –5».

Декарт определил правило символов, дающее возможность установить число положительных и отрицательных корней уравнения: «Настоящих корней быть может столько, сколько раз в нем меняются знаки + и –, а неверных столько, сколько раз встречаются попорядку два знака + либо два знака –». Потом он занес уточнение: при наличии надуманных («неосуществимых») корней уравнения число положительных корней может (а не обязано) быть равным числу перемен символов. Декарт высказал правила и на примерах показал, какие следует делать преобразования, чтоб поменять знаки корней уравнения, прирастить либо уменьшить корешки, получить уравнение, не содержащее второго члена, и т. д. «Просто, дальше, создать так, чтоб все корешки 1-го и такого же уравнения, бывшие неверными, стали настоящими, и совместно с тем все бывшие настоящими стали неверными; конкретно это можно создать, изменив на оборотные все знаки + либо –, стоящие на втором, четвертом, шестом и остальных, обозначенных четными местах, не изменяя знаки первого, третьего, 5-ого и им схожих, обозначенных нечетными числами мест».

Применив такое преобразование к уравнению (1), получим уравнение

х4
+ 4×3
— 19хх – 106x — 120 = 0, (2)

имеющее один положительный корень 5 и три отрицательных: –2, –3, –4.

Можно, не зная корней уравнения, прирастить либо уменьшить их на какую-либо величину, для что нужно создать подобающую подмену. к примеру, уравнение (2) опосля подмены х = у – 3 преобразуется к виду y3
– 8у2
– у + 8 == 0; его положительный корень 8 превосходит положительный корень уравнения (2) на 3.

Декарт увидел, что, «увеличивая настоящие корешки, мы уменьшаем неверные и напротив», при всем этом он имел в виду абсолютные величины корней.

правило исключения второго члена уравнения, известное еще Виету, Декарт иллюстрировал примерами.

Так, уравнение y4
+ 16y3
+ 71y2
– 4y –120 = 0 подстановкой z – 4 = у он сводил к

z4
– 25z2
– 60z – 36 = 0; его корешки –3, -2, -1, 6.

2-ой член уравнения x4
— 2ах3
+ х2
(2а2
— с2
) — 2aз
x + а4
= 0 он исключал подстановкой х = z + aего к виду z4
+ z2
(a2
– c2
) – z (a3
+ ac2
) + a4
– a2
c2
= 0.

Декарт гласил, что можно также «создать, чтоб все неверные корешки уравнения стали настоящими, но настоящие не стали неверными». Он утверждал, что просто примерно оценить величину неведомых отрицательных корней уравнения. В этом можно усмотреть постановку вопросца о границах реальных корней уравнения, которому потом уделил огромное внимание Ньютон.

Для умножения и деления неведомых корней уравнения на число, приведения дробных и иррациональных коэффициентов к целым Декарт воспользовался теми же подстановками, которые были известны и Виету. Разглядим пример.

Если положить у = х и z = 3у, то уравнение

x3
– x2
+ x – = 0

преобразуется поочередно в уравнение

y3
– 3y2
+ y – = 0, а потом в z3
– 9z2
+ 26z– 24 = 0.

Корешки окончательного уравнения 2, 3, 4; предшествующего – , 1, ; первого – , , .

О «воображаемых» (надуманных) корнях уравнения Декарт писал: «Как настоящие, так и неверные корешки не постоянно бывают действительными, оказываясь время от времени только воображаемыми. Иными словами, хотя постоянно можно вообразить для себя у всякого уравнения столько корней, сколько я произнес, но время от времени не существует ни одной величины, которая соответствует сиим воображаемым корням. Так, к примеру, хотя у уравнения х3
– 6xx + 13x–10 = 0 можно вообразить для себя три корня, но по сути оно имеет лишь один действительный, конкретно 2. Что касается 2-ух остальных корней, то сколько бы их ни наращивать, уменьшать либо множить так, как я лишь что растолковал, все равно их не получится создать другими, чем воображаемыми».

Еще одна очень принципиальная задачка алгебры была поставлена Декартом – задачка приводимости уравнений, т. е. представления целого многочлена с оптимальными (целыми) коэффициентами в виде произведения многочленов низших степеней. Декарт установил, что корешки уравнения третьей степени с целыми коэффициентами и старшим коэффициентом, равным единице, строятся при помощи циркуля и линейки (по другому говоря, уравнение разрешимо в квадратных радикалах) и тогда лишь тогда, когда уравнение имеет целый корень (т. е. левая часть его быть может представлена в виде произведения множителей первой и 2-ой степеней).

Для уравнения четвертой степени он также указал условие разрешимости; оно состоит в разрешимости его кубической резольвенты, т. е. соответственного уравнения 6-ой степени, кубического относительно у2
.

Декарт не показал, как он получил окончательный итог. Ф. Схоотен вывел резольвенту при помощи способа неопределенных коэффициентов. Он представил многочлен четвертой степени в виде x4
– px2
– qx + r = (x2
+ yx + z)(x2
– yx +v), откуда получил уравнения для нахождения у, z, у: z – y2
+ v = –p, –zy+vy = –q, vz = r.

Разрешающее уравнение (резольвента) имеет вид у6
– 2ру4
+ (р2
– 4г)y2
– q2
= 0.

В конце третьей книжки «Геометрии» Декарт графически решал уравнения третьей, четвертой, пятой и 6-ой степеней, отыскивая их корешки как пересечение неких линий.

Вклад Декарта в арифметику не ограничивается одной «Геометрией»: в его переписке содержатся решения почти всех задач, в том числе связанных с нескончаемо малыми.

§3 Обозначение производной и интеграла у Лейбница и развитие анализа.

Лейбниц занес большенный вклад в развитие математического анализа. Ему принадлежит создание почти всех знаков, которые мы используем на данный момент, к примеру, dx, ddx,…, d2
x, d3
x, , . Но знаки эти возникли у Лейбница не сходу. Сначало выражение = хu
(1)

у него смотрелось последующим образом: omn. xw = ult. х×omn. w – omn. omn. w. При всем этом он еще не употреблял обычного нам знака равенства.

В этом выражении omn. – исходные буковкы латинского слова omnia, т. е. все, – обозначает объединение, суммирование «всех» нескончаемо малых частей, стоящих под сиим знаком, х обозначает абсциссу точки на кривой, исходящей из начала координат, w в этих выкладках Лейбница обозначает то элемент дуги (ds), то дифференциал ординаты (dy), ult. – исходные буковкы латинского слова ultima (т. е. крайняя) – относится к абсциссе.

Для Лейбница в данном случае его omn.w выступает в роли новейшей функции, которая сама становится объектом операции, обозначенной omn. Как это событие, так и то, что он разглядывает итог неоднократного внедрения преобразования вида (1) и получает выражения, в каких операция omn. наслаивается несколько раз, принудило его находить наиболее комфортное обозначение, и в записи от 29 октября мы читаем: полезно писать заместо omn., так что будет заместо omn. (— это исходная буковка слова summa и Лейбниц именует этот символ суммой). И для новейшего исчисления, как в той же записи выражается Лейбниц, имеем

, , =, .

1-ое из этих соотношений соответствует преобразованию (1), а, b — неизменные, черта сверху играет роль скобки, и она, фактически, лишняя, ну и Лейбниц не постоянно ее пишет, но ее, пусть несистематическое, возникновение типично: так, в записи х мы лицезреем, что пишущему кажется нужным добавочно указать, что на х вправду множатся все , собранные в сумму знаком . Лейбниц дальше записывает (по поводу формул (2) и их вариантов): «Это довольно ново и броско, так как показывает на новейший вид исчисления», и перебегает к оборотному исчислению (contrariocalculo), вводя знак d, который «уменьшает измерение так, как наращивает », но пишет его в знаменателе (не dy, ay/d).

здесь же читаем: обозначает сумму, d — разность. Несколькими деньками позднее, в рукописи, помеченной 10 ноября, Лейбниц записывает: «dx — то же самое, что x/d, другими словами разность меж 2-мя наиблежайшими».

Замечательно то, что Лейбниц сходу, введя новое обозначение, начинает с ним обращаться как с эмблемой операции, отделяя его от объекта операций: он сходу отметил, что его «сумма» от (2-ух) слагаемых равна сумме «сумм» слагаемых и что неизменный множитель либо делитель можно выносить за символ «суммы». В записях следующих дней (от 1, 10, 11 ноября) он отмечает такие же характеристики операции, обозначенной через d. За эти деньки Лейбниц удостоверился, что d(xy) не то же самое, что dx×dy, и что d(x/y) ¹dx/dy, но не вывел еще соответственных формул. Отметил он и что , естественно, не то же самое, что . Он уже систематически употребляет обратность действий и d, к примеру, опосля равенства он пишет: либо wz = y2
/2d (здесь d еще в знаменателе). Отмечены им уже формулы для производной степенной функции при целых показателях степени, к примеру, «из квадратуры треугольника ясно, что y2
/2d = у; = из квадратуры параболы».

А в том, что он открывает тут нечто очень существенное, Лейбниц, возможно, совсем удостоверился, когда сумел применять пока вроде бы нащупываемый им метод при решении задач на оборотный способ касательных. Он писал: «Еще в прошедшем году я поставил впереди себя вопросец, который можно отнести к труднейшим во всей геометрии, так как всераспространенные до сего времени способы тут практически ничего не дают. сейчас я отыскал его решение и я приведу его анализ».

Свою задачку Лейбниц определяет как определение кривой, у которой поднормали назад пропорциональны ординатам. Таковая задачка сводится, в современных обозначениях, к решению дифференциального уравнения ydy/dx = k/y, где k — неизменная. Решение Лейбница состоит на самом деле в составлении такового уравнения и следующем его интегрировании при помощи разделения переменных. Он получил, таковым образом, уравнение разыскиваемой кривой, и она оказалась кубической параболой.

По записям Лейбница видно, что к середине 1676 г. он, располагая уже всеми главными правилами дифференцирования и интегрирования, решил еще несколько задач на оборотный способ касательных, в том числе известную в XVII в. задачку де Бона, предложенную в свое время Декарту, который не сумел получить ее общее решение. И это итог полностью самостоятельного хода мыслей. То, что Лейбниц знал к тому времени относительно результатов Ньютона и Грегори, не могло посодействовать ему пройти избранный им путь. Операционный подход Лейбница к дилемме и его поиски рациональной символики для новейшего исчисления, в чем более много выразилась творческая особенность Лейбница, были в достаточной мере чужды его английским конкурентам.

Приблизительно через год опосля открытий 1675 г., во время поездки по Голландии и опосля встречи там с Гудде, Лейбниц составил заметку, озаглавленную «Дифференциальное исчисление касательных». Она начинается записями:

d = 1, d = 2x, d = Зх2
и т. д.

d= –, d = –, d= – и т. д.

d=и т. д.

Отсюда выводится общее правило для разностей и сумм обычных степеней:

d= exe
-1
и, напротив, = (горизонтальная черта сверху значит взятие в скобки).

Как видно, тут символ d обозначает операцию вычисления производной. Но Лейбниц еще не полностью выработал к тому времени свою символику и чуток ниже можно прочесть, что «общее правило устанавливается так: и, напротив, ». Таковая редакция общепринятого правила следует за замечанием: «пусть у = x2
, тогда будет = 2x, как следует, = 2x». И на полях, возможно, позднее, Лейбниц написал, что это хорошее замечание к его исчислению разностей: «если by+ + etc. = 0, то b+ = 0, и так с остальными». тут он начинает свободно обращаться с дифференциалами, как это ему комфортно при решении дифференциальных уравнений, не предопределяя, какое из переменных независящее, какое функция.

Далее в том же наброске следует замечание, что вот, «возьмем какое-либо уравнение (но берется уравнение алгебраической кривой, притом второго порядка) … и напишем у +dy заместо у и схожим образом x + dx заместо х, тогда, опустив то, что опустить надлежит, получим другое уравнение» (т. е. оставляются лишь слагаемые первого порядка относительно дифференциалов, и это показано на примере).

Отсюда вытекает правило, обнародованное Слюзом, продолжает Лейбниц, и это, естественно, правильно. Здесь же он добавляет, что «мы нескончаемо расширим это правило: пусть букв будет сколько угодно и из их составлена формула, к примеру, из 3-х букв…». И Лейбниц сопоставляет уравнение алгебраической поверхности опять-таки второго порядка и небезупречно составленное методом дифференцирования соотношение меж дифференциалами, чтоб заявить без доп обоснования: «Отсюда явствует, что по такому способу получаем касательные плоскости поверхностей, и не имеет значения при всем этом, существует ли еще другое соотношение меж теми же знаками х, у, z, его ведь можно будет подставить позднее».

естественно, указание на то, как найти касательную плоскость к поверхности, следовало еще развить, что в рассматриваемом отрывке отсутствует, но мы лицезреем тут пример того, как Лейбниц равномерно, по различным поводам, ворачивается к собственному исчислению, расширяет область его внедрения, вместе с новенькими плодами получает с его помощью известные старенькые.

В 1678 г. Чирнгаус заявил Лейбницу, что нужно по способности избегать новейших обозначений, ибо это лишь затрудняет доступ к науке. Вот Виет заслуживает похвалы за то, что обходится буквенными обозначениями, не вводя новейших страшенных символов. Лейбниц, возражая подчеркивал, что нужно находить обозначения, которые коротко выражают заветную суть предмета, облегчая путь к открытиям и существенно понижая затрату интеллектуального труда. И таковы, продолжал Лейбниц, использованные мною знаки – я нередко с помощью их в несколько строк решаю самые трудные задачки.

В 1684 г. в «Лейпцигских ученых заметках» возникла одна из самых именитых математических работ: «Новейший способ максимумов и минимумов, также касательных, для которого не являются препятствием ни дробные, ни иррациональные величины, и особенный для этого род исчисления». В данной нам маленький статье даны базы дифференциального исчисления. Правила дифференцирования приводятся без доказательств, хотя есть указания на то, что тут все можно доказать, рассматривая дифференциалы как нескончаемо малые разности. Определение дифференциала функции дано как произведение производной (но производная задается геометрически как отношение ординаты к подкасательной) на дифференциал аргумента. Крайний можно задавать произвольно. Еще не вводится определенное соглашение относительно выбора знака для длин отрезков, которыми оперирует Лейбниц, потому он привод некие формулы с 2-мя знаками. В статье были опечатки, затруднявшие чтение, были и неверные утверждения (относительно определения точек перегиба). Но в ней были и действенные примеры внедрения новейшего метода, и создатель, приведя их, имел Право заявить: «Во всех таковых и много наиболее сложных вариантах наш способ владеет одной и той же поразительной и прямо беспрецедентной легкостью. Но это только начала некоторой наиболее высочайшей Геометрии, которая распространяется на труднейшие и прекраснейшие задачки прикладной арифметики, и чуть ли кому-нибудь получится заняться с той же легкостью таковыми вещами, не пользуясь нашим дифференциальным исчислением либо ему схожим».

Год 1690-й отмечает новейший шаг: начинается переписка и долголетнее научное общение Лейбница с Яковом Бернулли, а потом и его младшим братом Иоганном, написана 1-ая работа по анализу старшего из братьев, и оба они, арифметики первого ранга, с этого момента все усилия приложат для развития новейшего исчисления.

Через посредство И. Бернулли с новеньким исчислением знакомится и становится его приверженцем самый значимый французский механик тех лет П. Вариньон.

На Лейбница возникновение сторонников его способа и умножение примеров, показывающих плодотворность сделанного им исчисления, действовало стимулирующе.

Новейшие результаты Лейбница довольно многообразны. Некие из их относятся к технике дифференцирования. Так, в «Новеньком способе…» 1684 г. дифференцируются лишь алгебраические функции, оптимальные и иррациональные, и, в неявном виде, логарифм, а в 90-е годы Лейбниц, можно сказать, мимоходом в разных работах показывает дифференциалы синуса и арксинуса, функции вида uv
, где основание и показатель степени — функции независящего переменного, вводит дифференцирование по параметру. Позднее Лейбниц дает носящую его имя формулу для дифференциала хоть какого порядка от произведения функций. Можно сказать, что на данной нам стадии операция дифференцирования у Лейбница охватила весь припас узнаваемых тогда функций.

Иная группа результатов Лейбница относится к дифференциальной геометрии. один из более существенных – введение огибающей семейства плоских кривых, зависящих от некого параметра.

В третью группу можно соединить результаты по интегральному исчислению. Не считая формул, представляющих из себя воззвание упомянутых формул дифференцирования, Лейбниц отдал две работы о интегрировании оптимальных дробей (1701 и 1703 гг.). В первой из их он допустил ошибку, сделав вывод, что при наличии всеохватывающих корней у знаменателя рациональной дроби с действительными коэффициентами интегрирование обязано ввести новейшие непознаваемые функции, не считая оборотных радиальных и логарифмов. Когда же И. Бернулли указал верный итог, Лейбниц с ним не согласился и повторил свое неверное заключение во 2-ой работе. Эта ошибка Лейбница – не только лишь математический недосмотр, она имеет любознательные корешки. Утверждение, что интегралы вида

,

дают новейшие непознаваемые функции чудилось ему и симпатичным и правдоподобным еще поэтому, что это соответствовало лейбницевой метафизике. Если б все интегралы такового вида сводились, как выражается Лейбниц, лишь к квадратуре гиперболы (т. е. логарифмам) и к квадратуре круга (к оборотным радиальным функциям), то все было бы единообразно. «Но природа, мама нескончаемого контраста, либо, лучше сказать, божественный дух очень цепко бережет свою красивую многоликость, чтоб допустить слияние всего в одну породу. И таковым образом он находит роскошный и умопомрачительный выход в этом чуде анализа, этом побочном порождении мира мыслях, двояком существе вроде бы меж бытием и небытием, что мы называем надуманным корнем. И почему каждый раз, когда знаменатель рациональной дроби имеет надуманные корешки, что может получиться нескончаемо почти всеми методами, будет надуманной и гипербола, квадратура которой нам нужна, и ее никаким образом недозволено будет выстроить».

От Лейбница не ускользнуло и то, что интеграл можно разглядывать как дифференциал с показателем –1, и это привело его к введению дифференциалов всех отрицательных и дробных порядков при помощи безграничных рядов. Теорию интегралов и производных дробного порядка развивали в XVIII в. Эйлер, в XIX в. – Лиувилъ, Риман, Летников, в XX в. – Г. Вейль, М. Рис и др., и на данный момент она составляет один из разделов анализа. Лейбниц же 1-ый в печати указал на то, что операция интегрирования вводит произвольную постоянную и на связь меж определением первообразной функции и квадратурой. Он указал также, как интегрировать некие типы обычных дифференциальных уравнений. Значительно то, что Лейбниц ясно обусловил взаимоотношение интегрирования дифференциальных уравнений и интегрирования функций (1-ое следует считать выполненным, если оно сведено ко второму), и, аналогично, интегрирования функций и алгебраических операций (к примеру, определение корней знаменателя подынтегральной рациональной дроби считается при интегрировании задачей решенной).

Лейбниц много занимался также интегрированием иррациональностей (в конечном виде, как стали позднее выражаться) и глубоко просочился в сущность данной нам препядствия.

Наградой Лейбница является и применение к интегрированию и функций и дифференциальных уравнений безграничных рядов с внедрением способа неопределенных коэффициентов (крайний способ всходит к Декарту). Большое времени задач, как задачка Галилея о цепной полосы и задачка И. Бернулли о брахистрохроне.

Историческое лет, и за таковой сравнимо маленький срок математика преобразилась. Наука, в которую вступил Лейбниц, и наука, которую он оставил, принадлежит различным эрам, и это плод основным образом его трудов и трудов его школы. До Лейбница в необъятную область неизвестного пробовали просочиться то здесь, то там, наскоками, пусть порою весьма успешными, не имея общего плана. Благодаря Лейбницу разрозненные до этого усилия были подчинены общей программке, прояснились и близкие и дальние цели, средства для их заслуги оказались в распоряжении не только лишь сверходаренных одиночек и существенно выиграли в эффективности.

§ 4. язык кванторов и основания математической логики.

В связи с тем, что элементы логики представляют собой неотъемлемую составную часть школьного обучения арифметике, они должны изучаться в единстве с фактически математическим материалом на всех шагах обучения. Соответственный язык нужно вводить равномерно для обозначения уже разъясненных математических и логических понятий, чтоб в предстоящем он становился нужным компонентом обиходного математического языка.

4.1 Алгебра выражений.

Данная тема принципиальна для школьной арифметики. Не овладев ее главными действиями, недозволено осознать следующие темы, как, не овладев таблицами сложения и умножения, недозволено научиться математике и тем наиболее алгебре.

Начальные объекты алгебры выражений – это обыкновенные выражения. Их будем обозначать строчными латинскими знаками a, b, c, …, x, y, z. Предполагается, что всякое обычное выражение владеет одним и лишь одним из 2-ух параметров: или оно поистине, или неверно.

Будем воспользоваться практически везде принятой терминологией: характеристики истинности (и) и ложности (л) мы будем именовать значениями истинности выражений. При таковой терминологии

4.1.1 определения главных логических связок

а) Отрицание (символ ù ). Если а – выражение, то ùа (читается: «не а») также выражение; оно поистине либо неверно зависимо от того, неверно либо поистине выражение а.

Таковым образом, операция отрицания описывается последующей таблицей:

a
ùa

и
л

л
и

Мы лицезреем, что операция ù в теории выражений полностью соответствует понятию отрицания в обыденном смысле слова. Если, к примеру, а – выражение «Число три разделяет число 6», то отрицанием ùа этого выражения будет «Число три не разделяет число 6». Выражение а при всем этом поистине, выражение ùа, – неверно.

Если же в качестве выражения а взять какое-нибудь неверное выражение, к примеру «Число три разделяет число 5», то его отрицание ùа будет выражение «Число три не разделяет число 5» — настоящее выражение.

б) Конъюнкция. В качестве знака для конъюнкции мы будем употреблять символ Ù (можно также &).

Если а и b — выражения, то а Ùb (читается: «а и b») – новое выражение; оно поистине и тогда лишь тогда, когда а поистине и b поистине.

В отличие от операции отрицания, зависящей от 1-го простого выражения, конъюнкция, как и все следующие приводимые нами связки, зависит от 2-ух простых выражений, потому они именуются двуместными связками, отрицание же — связка одноместная.

Для задания двуместных связок комфортно записывать матрицы истинности в виде таблиц с 2-мя входами: строчки соответствуют значениям истинности 1-го простого выражения, столбцы – значениям другого простого выражения, а в клеточке пересечения столбца и строчки помещается

b

a

и
л

и
и
л

л
л
л

Как видно, определение операции конъюнкции полностью соответствует обыденному значению союза «и»:

в) Дизъюнкция. В качестве знака для дизъюнкции мы будем употреблять символ Ú.

Если а и b – выражения, то а Úb (читается: «а либо b») – новое выражение, оно неверное, если а и b неверны; во всех других вариантах а Úb поистине.

Таковым образом, матрица истинности для операции дизъюнкции смотрится так:

b

a

и
л

и
и
и

л
и
л

Операция дизъюнкции достаточно отлично соответствует обыденному значению союза «либо».

Примеры.

«Три разделяет 5 либо три больше 6» неверно;

«Три разделяет 6 либо три больше 6» поистине;

«Три разделяет 6 либо три меньше 6» поистине.

г) Импликация. В качестве знака для импликации будем употреблять символ Þ.

Если а и b – два выражения, то а Þb (читается: «а имплицирует b») – новое выражение; оно постоянно поистине, не считая того варианта, когда а поистине, а b неверно.

Матрица истинности операции импликации последующая:

b

a

и
л

и
и
л

л
и
и

В импликации а Þb 1-ый член а именуется антецедентом, 2-ой b – консеквентом.

Операция Þ обрисовывает в некой мере то, что в обыденной речи выражается словами «Если а, то b», «Из а следует b», «а – достаточное условие для b», но на данной нам аналогии не следует очень настаивать. Вправду, беря во внимание определение импликации, данное выше, и интерпретируя выражение а Þb как «если а, то b», мы получаем: «Если два раза два – четыре, то три раза три – девять» – настоящее выражение; «Если два раза два – 5, то три раза три – восемь» – настоящее выражение и лишь выражение типа «Если два раза два – четыре, то три раза три – восемь» неверно.

По определению импликации сложное выражение а Þ постоянно поистине, если консеквент настоящий либо если антецедент неверный, что в весьма малой мере отражает обыденное естественных науках.

Несколько позднее мы убедимся, что операция импликации довольно буквально выражает понятие логического следования в той форме, как оно употребляется в арифметике.

д) Эквиваленция. Для данной нам операции мы будем употреблять символ Û. Операция эквиваленции определяется так: если а и b – два выражения, то а Ûb (читается: «а эквивалентно b»; Û соответствует словесному выражению «…и тогда лишь тогда, когда…») – новое выражение, которое поистине, если или оба выражения истинны, или оба – неверны.

Из этого определения связки Û следует, что ее матрица истинности смотрится так:

b

a

и
л

и
и
л

л
л
и

Введенными пятью связками (ù, Ù, Ú, Þ, Û) мы ограничимся.

При помощи уже введенных связок мы можем строить сложные выражения, зависящие не только лишь от 2-ух, да и от хоть какого числа простых выражений.

Отметим в данной нам связи, что так называемое нестрогое неравенство а £b (читается: a меньше либо равно b») представляет собой дизъюнкцию (а < b) Ú (a = b); оно поистине, если поистине по наименьшей мере одно из входящих в него обычных выражений. Неплохими примерами сложных выражений, встречающихся в школьной практике, являются так именуемые двойные неравенства. Так, формула а < b < с значит (а < b) Ù (b < с), а, к примеру, а < b£c значит сложное выражение (а < b) Ù ((b < c) Ú (b = c)).

Построение сложных выражений делается аналогично тому, как в простой алгебре при помощи операций сложения, вычитания, умножения и деления строятся сколь угодно сложные оптимальные выражения. А конкретно, представим, что мы уже выстроили два каких-нибудь сложных выражения, которые мы ради удобства сокращенно обозначим большенными латинскими знаками А и В (при всем этом мы условимся, что простые выражения следует разглядывать как личный вариант сложных). Тогда новейшие выражения можно получить, соединив А и В одним из символов Ù, Ú, Þ, Û либо же построив выражение ùА и заключив итог в скобки. Сложными высказываниями будут, к примеру, выражения последующего вида:

((а Þb) Ù (с Ú а)); ((а Þb) Û (с Þùа)).

При всем этом предполагается, что встречающиеся тут буковкы являются сокращенными обозначениями каких-то выражений.

Таковым образом, в принципе зная эти выражения, можно было бы выстроить российские фразы, выражающие эти сложные выражения. Лишь словесное описание сложных выражений стремительно становится малообозримым, и конкретно введение целесообразной символики дозволяет проводить наиболее глубочайшее и четкое исследование логических связей меж разными высказываниями.

Располагая значением истинности обычных выражений, просто подсчитать на основании определения связок значение истинности сложного выражения. Пусть, к примеру, дано сложное выражение

((bÚ с) Û (bÙa))

и пусть входящие в него простые выражения имеют последующие значения истинности: а = л, b = и, с = и. Тогда bÚ с = и, bÙa = л, так что (( bÚ с) Û (bÙ а)), т. е. рассматриваемое выражение неверно.

4.1.2 Выражения и булевы функции

одной из главных задач алгебры выражений является установление значения истинности сложных выражений зависимо от значения истинности входящих в их обычных выражений. Для этого целенаправлено разглядывать сложные выражения как функции входящих в их обычных выражений. С иной стороны, потому что значение истинности (и либо л) сложного выражения зависит по определению логических связок не от самих обычных выражений, а только от их значения истинности, то можно считать, что хоть какое сложное выражение описывает функцию, аргументы которой независимо друг от друга принимают значения и либо л, а идет о функциях от нескольких аргументов из огромного количества {и, л} в огромное количество {и, л}, а только то, что данные огромного количества двухэлементны. Эти огромного количества часто обозначают не через {и, л}, а, к примеру, через {0, 1}, считая, что 1 значит «правду», а 0 – «ересь»).

Такие функции именуются булевыми функциями (по имени Д. Буля). К примеру, формула F (а, b, с) = (а Ùb) Þ (с Ù а) обрисовывает, беря во внимание определение входящих в нее связок, булеву функцию, задаваемую последующей таблицей:

а
b
с
F(a, b, с)
а
b
с
F(a, b, с)

и
и
и
и
л
и
и
и

и
и
л
л
л
и
л
и

и
л
и
и
л
л
и
и

и
л
л
и
л
л
л
и

Заметим, что булевых функций от n аргументов имеется только конечное число, а конкретно столько, сколько может быть многофункциональных таблиц. Число вероятных наборов аргументов равно 2n
, а любому набору аргументов можно независимо друг от друга сопоставлять одно из значений и либо л. Таковым образом, число различных булевых функций от n аргументов равно – Оно весьма стремительно вырастает с ростом n. исследование параметров булевых функций имеет большее естественно распространить определение высказывательных связок, потому что мы их обусловили выше, на булевы функции. Мы ограничимся рассмотрением только связок Ù, Ú, ù именуемых булевыми связками (либо булевыми операциями). Такое ограничение оправдано тем, что, как просто проверить, связки Þ и Û могут быть выражены через остальные булевы связки. С помощью таблиц истинности, приведенных выше, просто проверяются последующие тождества:

a Þ b º (ù a) Ú b;

a Û b º (a Ù b) Ú (ù a Ùùb),

которые разрешают везде поменять связки Þ, Û на Ù, Ú, ù.

Если мы сейчас имеем булевы функции {F (xl
, х2
, …, хn
), G (х1
, х2
, …, хn
)} от n переменных, то действие связок над ними определяется естественным образом:

F (xl
, x2
, …, хn
) ÙG (х1
, x2
, …, хn
), F (xl
, x2
, …,хn
) ÚG (xl
, x2
, …, хn
), ùF (xl
, x2
, …, хn
) – это такие булевы функции, которые принимают значения, предписываемые надлежащими таблицами для всякого вероятного значения аргументов. Коротко: булевы операции так переносятся на булевы функции, как деяния математики переносятся на обыденные функции числовых аргументов. Совершенно имеет пространство далековато идущая одной стороны, и высказываниями и булевыми функциями – с иной. При всем этом можно отметить, что в одном определенном смысле алгебра булевых функций проще алгебры числовых функций: если разглядывать только функции некого конечного числа аргументов, то таковых функций только конечное число. Потому выкладки с булевыми функциями полностью доступны осознанию школьников старших классов.

естественно, закономерности булевой алгебры наименее привычны и вызывают удивление и недоверие: это судьба всякого новаторства.

Выпишем законы булевой алгебры. Большенными латинскими знаками А, В, …, X, Y, Z мы обозначим объекты, над которыми осуществляются булевы операции Ù, Ú, ù. Для определенности будем считать, что эти объекты – булевы функции некого фиксированного числа переменных. Посреди их есть два особенных элемента: 1, 0. Это соответственно функции, принимающие для всех аргументов значения 0 и 1 (неизменные функции – нуль и единица). Тогда

А Ù В = В Ù А, AÚB = BÚA

AÙ (В ÙC) = (А Ù В) ÙCAÚ (В ÚC) = (А Ú В) ÚC

A Ù A = A A Ú A = A

A Ù 1 = A A Ú 1 = A

A Ù 0 = 0 A Ú 0 = A

ù(A Ù B) = ùA ÚùB ù(A Ú B) = ùA ÙùB

A Ù (B Ú C) = (A Ù B) Ú (A Ù C) A Ú (B Ù C) = (A Ú B) Ù (A Ú C)

ùùA = A

Если, как это обычно делают, булевы операции Ú, Ù, ù считать аналогом сложения, умножения и перехода к обратному числу, то некие из вышеприведенных законов те же, что для числового сложения и умножения, остальные же значительно различаются от обычных.

4.1.3 Задания для учащихся.

Правильно ли выражение: ù(205 кратно 5); 77; ù(8>10); 1£3£3.

А – огромное количество точек треугольника и В – огромное количество точек четырехугольника.

Верноливысказывание: CÎA Ù CÎB; KÎB Ù KÎA; SÎB Ú SÎA; ù(SÎA)ÙSÎB?

Понятно, что А=и, В=и, Х=л, Y=л. Найдите

АÚùХ; ùYÙùA; AÞX; ù(ùВÚY); (AÙB)ÚX; (XÚB)ÞY; (XÙA)Þ(YÚB); ù (AÚX)Ù(YÚùX).

Составьте таблицу истинности выражений: ùХÙХ; (ХÚY)ÚùY; (XÙY)ÚùX; ùXÞY; (XÙY)ÞY.

Используя переменные X, Y, Z, запишите сочетательное свойство операции «и».

Проверьте равенство (XÚY)ÙZº (XÙZ)Ú(YÙZ) и (XÙY)ÚZº(XÚZ)Ù(YÚZ), составляя таблицы истинности для левой и правой части.

4.2 Предикаты и кванторы.

4.2.1 Предикаты.

Алгебра предикатов – тот раздел математической логики, который конкретно надстраивается над алгеброй выражений.

Как мы лицезрели, одной из главных задач алгебры выражений является исследование истинности либо ложности выражений зависимо от истинности либо ложности входящих в их выражений. Невзирая на огромную значимость данной нам области логики, она оказывается очень бедной для описания и для исследования даже простых заключений науки и практики. В рамки алгебры выражений не укладываются ни простые заключения математики и геометрии, не говоря уже о достаточно сложных логических выводах, с которыми мы сталкиваемся в остальных науках и в ежедневной жизни.

Вправду, разглядим последующие простые заключения.

Из настоящих выражений «3 меньше 5» и «5 меньше 7» мы заключаем, что «3 меньше 7». Из настоящих выражений «Все птицы – звериные» и «Все воробьи – птицы» мы делаем заключение: «Все воробьи – звериные». Из выражений «Петр – отпрыск Ивана» и «Павел – отпрыск Петра» мы заключаем: «Павел – внук Ивана» и т. д.

Заметим, что во всех рассмотренных примерах истинность заключения зависит не только лишь от истинности посылок, да и от их содержания. Если поменять вид посылок, то может оказаться, что заключение будет неправильным. Так (в первом примере) из настоящих выражений «3 меньше 5» и «5 не равно 7» недозволено созодать заключение (которое оказывается настоящим), что «3 меньше 7», либо, изменив мало 2-ой пример, из настоящих выражений «Все птицы – звериные» и «Никакие рыбы не птицы» недозволено выводить ни неверное выражение «Никакие рыбы не звериные», ни настоящее выражение «Все рыбы – звериные». В конце концов, видоизменив крайний пример, из настоящих выражений «Петр – отпрыск Ивана» и «Павел – родственник Петра» мы не имеем права созодать заключение (которое в реальности быть может как настоящим, так и неверным), что «Павел – внук Ивана» (но можем вывести настоящее заключение: «Павел – родственник Ивана»).

Чтоб выстроить систему правил, позволяющую логически выводить правильные заключения, учитывающие в некий мере содержание посылок, мы должны проанализировать строение обычных выражений. И тут нам снова кое-что может дать подсказку грамматика. Следуя по такому пути, мы придем к разделу логики, именуемому алгеброй предикатов. Она подразумевает алгебру выражений уже известной, но идет далее: обыкновенные выражения, из которых состоят сложные, в свою очередь расчленяются.

Теория предикатов исходит из последующей установки. Обыкновенные выражения выражают, что некие объекты владеют некими качествами либо находятся меж собой в неких отношениях.

При всем этом понятия «свойство» и «отношение» рассматриваются как личные случаи общего понятия «предиката». Объекты, о которых говорится в высказываниях, именуются «термами». Попытаемся узнать смысл этих понятий на примерах.

Разглядим поначалу некое число обычных предложений – выражений, выражающих, что некий объект владеет неким свойством:

«Сократ – грек»;

«Платон – ученик Сократа»;

«Три – обычное число»;

«Василий – студент» и т. д. ,

Все приведенные примеры – обыкновенные предложения, Исходя из убеждений грамматики они состоят из подлежащего («Сократ», «Платон», «три», «Москва», «Василий») и сказуемого («есть грек», «есть ученик Сократа», «есть обычное число»). Подлежащее является наименованием некого объекта – определенного либо абстрактного, сказуемое выражает некое свойство. В латинской грамматике сказуемое именуется предикатом, и сиим термином принято сейчас воспользоваться в математической логике в рассматриваемых ситуациях. Главным для алгебры предикатов является 2-ой член предложения – сказуемое-свойство. Как алгебра предикатов трактует понятие «свойство»? Она разглядывает его как некую функцию последующим образом.

Возьмем 1-ый пример: «Сократ есть грек».

Заместо человека Сократ мы можем подставить имена различных людей и будем получать постоянно осмысленные предложения. Одни предложения будут настоящими, остальные – неверными:

«Сократ есть грек» – поистине;

«Платон есть грек» – поистине;

«Наполеон есть грек» – неверно;

«Ньютон есть грек» – неверно и т. д.

Наиболее обще можно разглядывать выражение вида «X есть грек», где буковка X показывает пространство, на которое необходимо подставить имя некого человека, чтоб получить выражение — настоящее либо неверное. Но, как нам уже понятно, значимым свойством выражения является его аргумент которой X пробегает класс всех людей, а сама функция воспринимает в качестве значений и либо л. Если мы будем, как это принято в арифметике, «X есть грек» записывать сокращенно, к примеру в виде Гр (X), то для значения X = Сократ получим Гр (Сократ) – и, а скажем Гр (Наполеон) – л и т. д. Относительно остальных приведенных примеров можно дословно повторить все то, что было сказано относительно первого.

Таковым образом, предикатом либо, лучше, предикатом-свойством будем считать функцию, определенную на неком всепригодном огромном количестве и принимающую значения и и л. Те элементы, для которых значение предиката «поистине», владеют данным свойством, другие не владеют.

Отсюда сходу видно, что в реальности всякий предикат-свойство полностью определяется подмножеством тех объектов, на которых данная функция воспринимает области математики. Таковыми будут, к примеру, характеристики натуральных чисел «быть обычным числом», «быть четным числом», «быть квадратом» и т. д.

Остановимся на примере «три есть обычное число» и на соответственном предикате-свойстве «быть обычным числом». Введем для этого характеристики сокращенное обозначение Пр (X). Предикат Пр (X) определен на огромном количестве натуральных чисел. Имеем Пр(1) = л (так как 1 не принято разглядывать как обычное число). Пр (2) = и, Пр (3) = и, Пр (4) = л, …, Пр (10) = л, Пр (11) = и и т. д.

Подобно приведенным предикатам-свойствам, математическая случае – n-местные дела. Рассмотренные выше предикаты-свойства числятся унарными предикатами. В конце концов, оказывается комфортным в понятие предиката-отношения как личный вариант включить и выражения в качестве «0 – местных предикатов».

Все математические дисциплины имеют дело с предикатами-отношениями, при этом самыми всераспространенными являются бинарные дела. Они описываются, разными словами: «равны», «не равны», «больше», «меньше», «разделять», «перпендикулярны», «параллельны» и т. д.

По аналогии с предикатом-свойством двухместным предикатом считается снова функция, сейчас от 2-ух аргументов, определенных на неком всепригодном огромном количестве, принимающая

Разглядим пример бинарного дела, определенного на огромном количестве натуральных чисел, а конкретно отношение, описываемое словом «больше». Если разглядывать это отношение как функцию от 2-ух переменных X и Y (на огромном количестве натуральных чисел), принимающую значения и либо л зависимо от того, будет ли соответственное отношение производиться либо нет, то эта функция описывает предикат, который обозначим через > (X, Y). Тогда имеем, к примеру, > (3, 2) = и, > (1, 3) = л, > (7, 5) = и и т. д. Наиболее много и обозримо двухместный предикаты >(Х, Y).

1
2
3
4
5
…

1
л
и
и
и
и
…

2
л
л
и
и
и
…

3
л
л
л
и
и
…

4
л
л
л
л
и
…

5
л
л
л
л
л
…

…
…
…
…
…
…
…

естественно, совершенно несложно указать в простой арифметике примеры трехместных предикатов и предикатов от еще большего числа аргументов. Так, трехместным предикатом является в геометрии отношение, описываемое словом «меж»: «Точка Y лежит меж точками Xи Z». В математике отлично известны понятия большего общего делителя и меньшего общего кратного 2-ух целых чисел: фраза «Число d является большим общим делителем чисел а и b» обрисовывает трехместный предикат. Трехместные предикаты на огромном количестве реальных чисел задают деяния сложения, вычитания, умножения и деления: X + Y = Z, X – У = Z, X • Y = Z, X : Y = Z. Примером четырехместного предиката может служить отношение меж членами пропорции X : Y = Z : W

Ознакомившись с понятием предиката, мы перебегаем сейчас к рассмотрению операций, позволяющих из неких начальных предикатов строить новейшие. Начнем исследование с простого варианта одноместных предикатов. Пусть Р (X) и Q (X) – два одноместных предиката, определенных на неком огромном количестве М. При помощи операций алгебры выражений мы можем строить новейшие предикаты на огромном количестве М. Конъюнкция Р (X)ÙQ (X) – это предикат R1
(X) = Р(X)ÙQ(X), который истинен для тех объектов а из М, для которых оба предиката Р(X) и Q(X) истинны. Аналогично определяется дизъюнкция Р(X)ÚQ(X):R2
(X) = Р(X)ÚQ(X) – это предикат на М, который истинен в точности для тех аМ, для которых истинен по наименьшей мере один из предикатов Р (X) и Q (X). Так же определяется отрицание ùР (X): R3
(X) = ùР(X) – предикат на М, настоящий для тех и лишь тех а Î М, для которых Р (X) ложен.

4.2.2 Кванторы.

В алгебре предикатов вместе с операциями логики выражений самую важную роль играют операции, именуемые кванторами. Конкретно употребление кванторов делает алгебру предикатов существенно наиболее богатой, чем алгебру выражений. Кванторы соответствуют по смыслу тому, что на обыкновенном языке выражается словами «все» («для всякого», «для всех» и т. п.) и «существует» («некий», «найдется» и т. п.).

понятие, обозначаемое словом «все», лежит в базе квантора всеобщности (либо квантора общности). Если через Гр (X) обозначен предикат «X есть грек», определенный на огромном количестве М всех людей, то из этого предиката при помощи слова «все» мы можем выстроить выражение «Все люди – греки» (естественно, неверное выражение). Это пример внедрения квантора всеобщности.

Совершенно же квантор всеобщности определяется так. Пусть Р (X) – какой-либо предикат. Тогда квантор всеобщности – это операция, которая сопоставляет Р (X) выражение

«Все X владеют свойством Р (X)».

Для данной нам операции («все») употребляется символ (перевернутая латинская буковка А, напоминающая о германском слове «alle» либо британском «all» – все). Выражение

записывается так: (X)P(X) (читается: «для всех X Р от X»). В согласовании со смыслом слова «все» (X)Р(X) – неверное выражение, не считая того единственного варианта, когда Р (X) тождественно-истинный предикат.

вместе с квантором всеобщности в логике предикатов рассматривается иной квантор – «двоякий» ему квантор существования, обозначаемый знаком (это перевернутая латинская буковка E, напоминающая германское слово «existieren» либо английское «exist» — существовать):

(Х)Р(Х)

(читается: «существует такое X, что Р от X») – выражение, которое поистине и тогда лишь тогда, когда Р поистине по наименьшей мере для 1-го объекта а из области определения М. Тем (X)Р(X) – настоящее выражение для всех предикатов Р (X), не считая 1-го – тождественно-ложного.

Меж кванторами и имеют пространство дела равносильности, дозволяющие сводить хоть какой из этих кванторов к другому: ù(X) P(X) Û(X) ùP(X) («Ошибочно, что все Xобладают свойством Р (X)» равносильно тому, что «Существует таковой объект X, для которого поистине не Р (X)»). Отсюда имеем: (X) Ûù(X)ùP(X). Аналогично, имеет пространство двоякий законù (X) P(X) Û(X)ùP(X). («Ошибочно, что существует X, владеющее свойством Р (X)» равносильно «Все X владеют свойством не Р (X)»).

Отсюда (X)Р(X)Ûù(X)ùP(X). Эти равносильности именуют правилами де Моргана для кванторов.

При помощи квантора существования просто выражается суждение типа «Некие Р сущность Q» (к примеру, «Некие британцы курят», «Некие нечетные числа – обыкновенные» и т. п.), т. е. что по последней мере один объект а, владеющий свойством Р, владеет также свойством Q. Данный факт записывается формулой (X)(Р(X)ÙQ(X)) («Существует таковой X, что Р от X и Q от X»).

Аналогично при помощи кванторов записывается ряд остальных отношений меж одноместными предикатами.

Еще наиболее богатые способности открывает применение кванторов к многоместным предикатам. Остановимся кратко на этом вопросце.

Пусть А (X, Y) – некий двухместный предикат, определенный на неком огромном количестве М. Квантор всеобщности и квантор существования можно использовать к нему как для переменной X, так и для переменной Y: (X)А(X, У); (Y)А(X, Y); (X)А(Х,Y); (Y)A(X,Y). Переменная, к которой использован квантор, именуется связанной, иная переменная – вольной. Все четыре приведенных выражения являются записями одноместных предикатов от соответственной вольной переменной. (X)А(X,Y) (читается: «для всех X, A от X и Y») – одноместный предикат от переменной Y: (X)А (X,Y)=F(У), Он истинен в точности для тех bÎМ, для которых одноместный предикат А (X, b) истинен для всех X. Если представить предикат А (X, Y) его таблицей, то предикат F (Y) = (X) (X, Y) истинен для тех b, для которых столбец с входом b содержит только буковку и.

Применение квантора к одной из переменных двухместного предиката превращает его в одноместный. В случае трехместных предикатов применение квантора приводит к двухместному предикату. Аналогично и для предикатов с огромным числом мест применение квантора превращает n-местный предикат в (n – 1)-местный.

К вольной переменной X одноместного предиката (У)А(X, Y) в свою очередь можно использовать квантор всеобщности либо квантор существования. Получаются выражения

(X)((У)А(X,У)); (X)((Y)А(X,У)), которые, опуская скобки, принято записывать несколько проще: (X)(У)А(X,У); (X)(Y)А(X,У),

Это – выражения. 1-ое поистине, если все строчки, а тем и вся таблица предикатов, содержат лишь буковку и, 2-ое поистине, если соответственная матрица содержит по наименьшей мере одну тождественно-истинную строчку. Три остальные предиката (X)А (X,У), (У)А(X, У) и (X)А (X,У) также допускают квантификацию, так что в общей трудности мы получаем из 1-го предиката восемь формально разных выражений: (X)(У)А (X, У); (X)(У)А (X,У); (X)(У)А (X, У); (X)(У)А (X, У); (У)(X) А (X, У); (У)(X)А(X, У); (У)(X)А (X, У); (Y) (X) А (X, У).

Несложно убедиться в том, что четыре выражения, содержащие схожие кванторы, попарно эквивалентны:

(X)(У)А(X,У) Û(У)(X)А (X, У);

(X)(У)А (X, У) Û(Y)(X)А (X, У).

(X)(У)А(X,У) так же как и (У)(X)А(X, У), поистине и тогда лишь тогда, когда А (X, У) – тождественно-истинный предикат, (X)(У)А (X, У) и (Y)(X)А(X,У) оба истинны во всех вариантах, не считая 1-го, когда А(X,У) – тождественно-ложный предикат. Все другие выражения значительно различны. В особенности следует держать в голове, что порядок следования разноименных кванторов весьма важен.

Я считаю, что к окончанию школы ученики должны завладеть кванторами, но введение их обязано быть постепенным и начинаться в обычных ситуациях. Учащиеся должны отлично осознавать, что от перестановки кванторов может изменяться смысл утверждения.

к примеру, Пусть I=(а,b) – некий интервал. Тогда «Для всякого хÎI существует таковой у, что у = f (х)» ((x)(у) (у = f (х))), значит, что функция f(х) везде определена на I. Напротив, «Существует такое у, что для всякого х у=f (х)» ((у)(х)(у=f(х))) значит, что функция f(x) воспринимает для всех х некое фиксированное

Приведем очередной пример. Корректное определение периодичности везде определенной функции f(х) смотрится с внедрением кванторов так: (c)(x) (c¹0 ÙÙf(x+c) = f(x)), меж тем если переставить кванторы и сконструировать утверждение «Для всякого х существует такое с, что с¹0 и что f(х + с) =f(x)»: (c)(x) (c¹0 Ùf(x+c) = f(x)), то это значит только, что функция воспринимает каждое совершенно другое.

В математическом анализе нередко приходится сталкиваться с кванторами.

Определение предела последовательности из учебника «Алгебра и начала анализа» для 10-11 классов сформулировано так «Число А является пределом последовательности аn
, если для хоть какого >0 существует номер N, таковой, что при всех n>N правильно неравенство ». В кванторном обозначении это определение записывается так:

( >0)(NÎN)(nÎN)((n>N) Þ

Переставлять кванторы недозволено: конкретно тот факт, что N под квантором существования следует за выражением (> 0), показывает на зависимость N от избранного .

Как выразить утверждение, что последовательность (хn
) сходится? нужно указать на то, что предел A существует. При помощи кванторов это утверждение формулируется так:

(A) (> 0) (NÎN) (nÎN)((n > N) Þ ()).

Таковая запись имеет к тому же то преимущество, что она практически автоматом дозволяет формулировать отрицание существования предела, значащее свойство расходимости. Для этого довольно несколько раз применить правило де Моргана для кванторов: (хn
) расползается Ûù((A) (> 0) (NÎN) (nÎN)((n > N) Þ ()) Û(A)(> 0) (NÎN) (nÎN)((n > N) Ù).

Задания для учащихся.

Установите, какие из последующих выражений истинны.

x (x + 1 = x); x (x2
+ x + 1>0); x (x2
— 5x + 6>0); x (x2
-6x+8³0 Ùx2
-4x+3>0); x (x2
— 5x + 6 ³ 0 Úx2
+ 5x + 6 < 0)

2) При каких аÎR истинны последующие выражения: х (x2
+x + а>0);

x (x2
+x + а>0); х (x2
+ax + 1>0);

3) Пусть P(x) = «х – обычное число»

E(x) = «х – четное число»

Z(x) = «х – целое число»

D(x,y) = «y делится на х»

G(x,y) = «х > y»

Расшифруйте последующие выражения и выясните, какие из их истинны:

P(x)ÞùE(x); x (E(x) Ú D(x,6));

x(P(x)ÞùE(x); x(P(x)ÚE(x));

xy(D(x,y)ÞG(y,x)); xy(Z(x)ÙZ(y)ÞD(x,y));

xy(Z(x)ÙZ(y)ÞD(x,y)).

4) Запишите при помощи кванторов определение предела функции: число b именуется пределом функции f(х) при х, стремящемся к а, если для хоть какого положительного числа найдется такое положительное число , что при всех х ¹ а, удовлетворяющих неравенству ½х – а½<0, будет выполнено неравенство ½f (х) – b½< .

§5 Методические советы к теме «Введение нуля и развитие позиционной десятичной системы счисления».

В 5 классе уже может быть обсуждение с учащимися данной нам темы.

Можно вспомянуть с ними, что счет у нас ведется десятками: 10 единиц образуют один десяток, 10 10-ов – одну сотку и т.д., другими словами: 10 единиц первого разряда образуют одну единицу второго разряда, 10 единиц второго разряда – одну единицу третьего разряда и т.д.

Таковой метод счета, группами в 10, которым мы пользуемся, именуется десятичной системой счисления. Число 10 именуется основанием десятичной системы счисления. Строго определения десятичной системы давать не стоит.

Потом, необходимо обсудить, почему мы считаем конкретно десятками, другими словами как появилась десятичная система счисления?

люди на первых ступенях развития общества считали при помощи 10 пальцев рук. на данный момент время от времени молвят: «Пересчитать по пальцам».

Дальше следует побеседовать о том, что были племена и народы, которые при счете воспользовались только пятью пальцами одной руки, считали пятками, потому и употребляли они пятеричную систему счисления, в какой основой служит число 5.

Есть и остальные системы счисления: двоичная, двадцатеричная (следы ее сохранились до сего времени во французском языке – они молвят заместо «восьмидесяти» — «четырежды 20»). Двадцатеричная система появилась у народов, считавших не только лишь при помощи пальцев рук, да и пальцев ног. Античные вавилоняне воспользовались шестидесятеричной системой счисления.

Можно обсудить, сколько цифр употребляется в каждой из перечисленных систем счисления для изображения чисел.

Также полезно для учащихся будет ознакомиться с римской нумерацией, обсудить где она применяется. Учащиеся должны научиться записывать арабские числа при помощи римских. здесь же можно предложить им пару занятных задач, где употребляют римские числа с целью вербования их внимания.

больше никакие алфавитные системы не стоит затрагивать, а лишь показать табличку с алфавитными нумерациями, также числовые знаки разных народов (см. далее).

Опосля этого учащимся можно сказать кратко о происхождении знака 0.

необходимо отметить, что на данный момент нуль это не попросту символ для отделения разрядов, а число, которое можно ложить, вычитать, множить и разделять, как и остальные числа. Единственное ограничение – разделять на 0 недозволено.

Может быть вынесение этого материала на факультативные занятие, где дискуссии разных систем счисления можно отвести больше времени.

С учащимися 7-8 классов может быть наиболее полное рассмотрение данной нам темы.

Начать следует с рассказа о том, что есть позиционные и непозиционные системы счисления. Отдать определения одной и иной системы счисления, попросить учащихся привести примеры.

Потом можно обсудить двоичную систему. Учащиеся должны научиться переводить числа из двоичной системы счисления в десятичную, и напротив. Опосля этого подобные деяния сделать с иной системой счисления, к примеру, пятеричной. Можно обучить учащихся ложить и множить числа в разных системах счисления, хороших от десятичной. Дальше, я считаю, что необходимо разглядеть десятичную непозиционную систему (к примеру, старых египтян). Учащиеся должны осознать, как тяжело изображать огромные числа в непозиционных системах счисления. Лишь тогда они сумеют по достоинству оценить заслугу индийских математиков, которые сделали десятичную позиционную систему счисления.

До этого чем начать рассказ о происхождение знака нуля можно предложить учащимся записать число 100 три тыщи двести 50 при помощи цифр, но не используя знака нуля. Обсудить как они это сделали, дальше предложить сложить это число с числом 20 тыщ семьсот восемьдесят девять, снова таки записанного при помощи цифр, но без знака нуля. У учащихся возникнут некие затруднения. Опосля этого будет целенаправлено поведать им о заслуге индийцев.

Если кто-то из учащихся заинтересуется нумерациями разных народов, то можно предложить им для самостоятельного исследования книжку Э. Кольмана «История арифметики в древности».

Перечень литературы

Алексеев Б. Т. Философские препядствия формализации познания. Издательство ленинградского института. 1981.

Бурбаки Н. Очерки по истории арифметики. М., издательство зарубежной литературы. 1963.

Вилейтнер Г. История арифметики от Декарта до середины XIX столетия. М., «Наука». 1966.

Выгодский М.Я. Математика и алгебра в старом мире. М., «Наука». 1967.

Глейзер Г.И. История арифметики в школе. Пособие для учителей. Под ред. В.Н. Молодшего. М., «Просвещение», 1964.

Калужнин Л.А. Элементы теории множеств и математической логики в школьном курсе арифметики. Пособие для учителей. М., «Просвещение», 1978. 88с.

Нешков К.И. И др. Огромного количества. дела. Числа. Величины. Пособие для учителей. М. «Просвещение», 1978. 63 с.

Марков С.Н. Курс истории арифметики: Учебное пособие. – Иркутск: Издательство иркутского института, 1995. – 248с.

Молодший В.Н. Очерки по истории арифметики. М.

Никифоровский В.А. Из истории алгебры XVI-XVII вв.. М., «Наука». 1979.

Петров Ю.А. Философские препядствия арифметики. М., «Познание», 1973.

Погребысский И.Б. Гольфрид Вильгельм Лейбниц. М., «Наука». 1971.

Рыбников К.А. История арифметики. Издательство столичного института. 1974.

Таваркиладзе Р.К. О языке школьного курса арифметики. «Математика в школе».

Хрестоматия по истории арифметики. Математика и алгебра. Теория чисел. Геометрия. Пособие для студентов физ.-мат. фак. пед. институтов. Под ред. А.П. Юшкевича. М., «Просвещение», 1976.

Энциклопедический словарь молодого математика. М., «Педагогика». 1989.

]]>