Учебная работа. Реферат: Учебники математики в прошлом, настоящем и будущем

Учебная работа. Реферат: Учебники математики в прошлом, настоящем и будущем

Введение

Вопросцы о том, как складывались первичные математические представления, какой вид они воспринимали, как проходили 1-ые этапы их совершенствования, никогда не теряли собственной актуальности и не растеряют ее в дальнейшем. В том, чтоб верно освещать эти вопросцы, заинтересованы очень широкие слои людского общества: и те, кто начинает свое математическое образование; и те, кто учит деток арифметике, потому что это содействует отысканию и использованию более действенных методических приемов.

Своеобразие задачи заключается в том, что поиски реального начала математических познаний населения земли уводят нас в седоватую, еще дописьменную древность…

Причина выбора данной темы, цель работы

Причина выбора нами данной темы весьма ординарна; мы желали, как можно больше выяснить о том, как развивалась математика, как проводилось обучение в разные времена и что предшествовало тому, что мы имеем на данный момент. Также охото осознать ту тенденцию, с которой совершенствовались сами учебники, поначалу в виде обычных записей, а потом, со временем, обретя нынешний вид.

Мы попытаемся выяснить, с чего же началось обучение арифметике, для чего это потребовалось, как в протяжении веков изменялось отношение к обучению и как это сказалось на развитии науки, в данном случае – арифметики. Также мы выясним у самих учеников то, вроде бы они сами желали ее учить. Другими словами попытаемся представить, какими станут учебники в не далеком будущем.

Начало формирования арифметики

Начнем с описания того, как складывалось понятие о числе (на первых порах натуральном, т.е. целом положительном). Естественным представляется выражение, что это понятие появилось и сформировалось в итоге неоднократно используемой (в силу практической необходимости) операции счета, перечисления предметов. Но, невзирая на кажущуюся простоту, естественность, свою «изначальность», операции счета не является по сути первичной, простейшей. Она возникает и применяется на уже сравнимо высочайшем уровне развития математических частей мышления. Ей предшествовало, как выясняется, несколько ступеней усовершенствования логических суждений.

История населения земли со всей очевидностью указывает, что даже самые. Чудилось бы, изначальные понятия людей не являются прирожденными (и уж тем наиболее не посланы «выше»). Они сущность отражения параметров и отношений настоящих предметов беспристрастно имеющегося мира. Приобретены они в процессе активной деятель людей. Конкретно благодаря труду и сопровождающей его членораздельной речи, обычно расположенный в головном отделе тела и представляющий из себя малогабаритное скопление орган животного, служащий для передачи в обычно расположенный в головном отделе тела и представляющий собой компактное скопление нервных клеток и их отростков»> обычно расположенный в головном отделе тела и представляющий собой компактное скопление нервных клеток и их отростков»>мозг и органы эмоций человека достигнули значимого совершенства. В итоге опосля долговременной эволюции, обычно расположенный в головном отделе тела и представляющий из себя малогабаритное скопление служащий для передачи в нервных человека выработал возможности создавать абстракции, нужные для счета и измерения.

По мере перехода людей на наиболее высочайший уровень умственного развития чувствительный счет оказался недостающим. Возникает необходимость ассоциировать огромного количества, к примеру, поэлементно сопоставляя их численность. Возникает она в большей степени в процессе общения людей. Так начинают появляться записи, где бытуют символические обозначения чисел и деяния над ними.

До этого всего, заслуживает внимание то, что в ряде ранешних источников содержатся выражения, говорящие о преемственности математических и совершенно научных познаний. Так, в их упоминается о поездках негоциантов и образованных людей древнегреческих полисов в остальные страны. Почаще идет речь о Египте и других странах Близкого Востока, о развитии в их науки и о технических достижениях. Практический нрав арифметики и успехи ее в этих странах были оценены высоко и восприняты вполне.

Дальше мы разглядим, как проходило развитие арифметики в разных цивилизациях и почему росла Потребность передачи познаний из поколения в поколение.

Старый Египет

Египтяне употребляли арифметику, чтоб вычислять вес тел, площади посевов и объемы зернохранилищ, размеры податей и количество камешков, требуемое для возведения тех либо других сооружений. Наше познание древнеегипетской арифметики основано основным образом на 2-ух папирусах, датируемых приблизительно 1700 до н.э. Излагаемые в этих папирусах математические сведения всходят к еще наиболее преждевременному периоду – около 3500 до н.э. В папирусах можно отыскать также задачки, связанные с определением количества зерна, нужного для изготовления данного числа кружек пива, также наиболее сложные задачки, связанные с различием в сортах зерна; для этих случаев рассчитывались переводные коэффициенты.

Но главной областью внедрения арифметики была астрономия, поточнее расчеты, связанные с календарем. Календарь употреблялся для определения дат религиозных праздничков и пророчества каждогодних разливов Нила. Но уровень развития астрономии в Старом Египте намного уступал уровню ее развития в Вавилоне.

Древнеегипетская письменность основывалась на иероглифах. Система счисления того периода также уступала вавилонской. Египтяне воспользовались непозиционной десятичной системой, в какой числа от 1 до 9 обозначались подходящим числом вертикальных черточек, а для поочередных степеней числа 10 вводились личные знаки. Поочередно сочитая эти знаки, можно было записать хоть какое число. С возникновением папируса появилось, так называемое, иератическое письмо – скоропись, способствовавшее, в свою очередь, возникновению новейшей числовой системы. Для всякого из чисел от 1 до 9 и для всякого из первых 9 кратных чисел 10, 100 и т.д. употреблялся особый опознавательный знак. Дроби записывались в виде суммы дробей с числителем, равным единице. С таковыми дробями египтяне производили все четыре арифметические операции, но процедура таковых вычислений оставалась весьма массивной.

Геометрия, у египтян, сводилась к вычислениям площадей прямоугольников, треугольников, трапеций, круга, также формулам вычисления размеров неких тел. нужно сказать, что математика, которую египтяне употребляли при строительстве пирамид, была обычный и примитивной.

задачки и решения, приведенные в папирусах, сформулированы чисто рецептурно, без любых разъяснений. Египтяне имели дело лишь с простейшими типами квадратных уравнений и арифметической и геометрической прогрессиями, а поэтому и те общие правила, которые они смогли вывести, были также самого простого вида. Ни вавилонская, ни египетская арифметики не располагали общими способами; весь свод математических познаний представлял собой скопление эмпирических формул и правил.

Хотя майя, жившие в Центральной Америке, не оказали воздействия на развитие арифметики, их заслуги, относящиеся приблизительно к 4 в., заслуживают внимания. Майя, по – видимому, первыми употребляли особый знак для обозначения нуля в собственной двадцатеричной системе. У их были две системы счисления: в одной применялись иероглифы, а в иной, наиболее всераспространенной, точка обозначала единицу, горизонтальная черта – число 5, а знак обозначал нуль. Позиционные обозначения начинались с числа 20, а числа записывались по вертикали сверху вниз.

В те времена бумаги еще нигде не было. В Месопотамии писали, к примеру, на табличках из сырой глины, которые позже обжигали. В неких странах писали на пергаменте. Египтяне же изобрели дешевенький и удачный писчий материал, по своим качествам весьма близкий к бумаге – листы из папируса, которые можно было склеивать в свитки хоть какой длины. Ученые долгие годы пробовали разгадать секрет старых мастеров. Он должен был быть обычным, потому что папируса требовалось много.

Папирус ранее обильно рос в болотистых районах Нижнего Египта, где сейчас его нет. Он играл в Египте гигантскую роль: из него изготовляли веревки, корзины, картонаж, корзинки, лодки и т.д., но основная Ценность – изготовка материала для письма. Папирус рос весьма стремительно, давая новейшие побеги круглый год. По берегам Нила были густые заросли папируса высотой до 2 – 3 метров.

Собирали папирус ранешным с утра, потом отвозили в мастерскую. Привезенные стволы складывали на землю и, до этого чем палящее солнце успевало подсушить их, стремительно порезали на огромные кусочки. Потом мастера особыми ножиками осторожно сдирали зеленоватую кожицу со стеблей, обнажая мягенькую белоснежную сердцевину. сейчас сердцевину было надо разрезать вдоль на несколько тонких полосок, но весьма буквально и осторожно. На ровненьком особом столе полосы укладывали в ряд, слегка внахлест, на кусочек плотной ткани , кропотливо подгоняя друг к другу. Поверх первого ряда, поперек него, клали 2-ой, буквально таковой же ряд полосок. Все это покрывалось узкой материей отлично поглощающей воду, и в течение часа либо 2-ух работники безпрерывно колотили по ней древесными молотками, стараясь ничего не двинуть с места. Потом они осторожно клали на объединённых общим происхождением легкий пресс и оставляли на несколько часов. За это время сок, выступивший из папируса, прочно склеивал полосы, и они преобразовывались в сплошной лист узкой белоснежной бумаги. Когда лист просыхал, его аккуратненько порезали на кусочки и склеивали в полосы разной длины, обычно от метра до 2-ух, но часто владелец мастерской получал заказы и на весьма огромные папирусы — до 20 метров. Папирус разглаживали круглыми гладкими камнями либо лопаточками из слоновой кости, чтоб тростниковое перо могло просто двигаться по нему, сворачивали в трубочки и перевязывали шнурами. На последующий денек его везли на продажу.

Папирус сберегали: нередко старенькые записи аккуратненько смывались, листок высушивался, и потом снова употреблялся. Когда листок папируса исписывали до конца, к нему подклеивали иной. Книжка выходила все длиннее. Для хранения ее сворачивали в свиток. Некие книжки выходили до сорока метров.

Папирус Ринда





Источниками для исследования древнеегипетских математических познаний являются два папируса – папирус Ринд, (Лондон, Английский музей) и Столичный математический папирус (Москва, ГМИИ им. А.С.Пушкина). Оба — копии наиболее ранешних текстов: папирус Ринда был переписан в XVIII династию с оригинала эры Среднего королевства; Столичный папирус, датируемый временем правления фараонов XII династии, отражает еще наиболее ранешний документ. Эти монументы тяжело именовать научными трактатами в нашем осознании данного определения, ибо они не содержат характерного современным работам осмысления теоретических заморочек, таковых как анализ либо подтверждение корректности того либо другого решения. Напротив, в их даны условия различных практических задач – измерения площади поля, вместимости амбара, раздел имущества и т.д. (в папирусе Ринда их 80, в Столичном — 25).

Вослед за условием задачки следует метод решения и указан верный ответ. Можно представить, что эти папирусы были учебными пособиями по выполнению определенных операций.

Математические папирусы демонстрируют высокие заслуги Старого Египта в области математического познания. Но они не дают представления о степени осмысления этого познания самими египтянами – заинтересовывало ли их теоретическое развитие арифметики либо же они хлопотали лишь о ее практическом применении? Не считая того, нет неопровержимых доказательств, что пропорции строительных сооружений, таковых как пирамиды, не были результатом обеспеченного опыта и чутья строителей, а заблаговременно просчитывались. Но одно, непременно: за тыщу лет до Архимеда и Пифагора египтяне открыли и удачно применяли на практике законы, вошедшие в сокровищницу древней, а потом и мировой математической мысли.

задачки математических папирусов

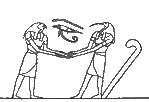
Тот и Хор с «Оком Хора». Фрагмент росписи гробницы Сети I

Посреди задач математических папирусов можно выделить чисто алгебраические (№ 24-28 папируса Ринда и №1,19 и 25 Столичного папируса), показывающие, что египтяне могли решать линейные уравнения с одной неведомой х, именуемой «куча» (типа ax + bx+…+cx =d), также возводить в степень и извлекать корень.

Папирус Ринда содержит задачки на вычисление геометрической (№79) и арифметической прогрессии: «Для тебя сказано поделить 10 «хекат» ячменя меж 10 людьми так, чтоб разница меж каждым человеком и его соседом составляла 1/8 «хекат» ячменя. Средняя толика есть 1 «хекат». Возьми 1 из 10, остаток есть 9. Составь половину различия — это есть 1/16 «хекат». Приложи ее к средней доле. сейчас ты должен рассчитать для всякого лица по 1/8 «хекат», пока не достигнешь конца» (Ринд, №64).

Египтяне также решали и геометрические задачки – вычисляли площадь треугольника, прямоугольника, круга и даже поверхности шара. Они высчитали число ∏ — отношение длины окружности к поперечнику — с точностью до 0,6% (3,16 заместо 3,14).

Математические папирусы являются свидетельством знакомства египтян со стереометрией. Описаны методы вычисления размера цилиндра, призмы и пирамиды: «Если для тебя именуют усеченную пирамиду 6 локтей в высоту, 4 – в нижней стороне, 2 – в верхней, вычисляй с 4. Возводя их в квадрат, получаешь 16. Удвой 4, получишь 8. Сложи 16 с этими 8 и с этими 4. Выходит 28. Вычисли 1/3 от 6. Выходит 2. Вычисли 28 2 раза. Выходит 56. Смотри! Он есть 56. Ты отыскал верно» (Столичный папирус).

Наши зания о древнеегипетской арифметике основаны основным образом на 2-ух огромных папирусах математического нрава и на нескольких маленьких отрывках. один из огромных папирусов именуется математическим папирусом Ринда (по имени обнаружившего его учёного) и находится в Лондоне. Он приблизительно 5,5 м длины и 0,32 ширины. иной большенный папирус , практически таковой же длины и 8 см ширины, находится в Москве. Находящиеся в их математические сведения относятся приблизительно к 2000 г. до н.э.

Папирус Ринда представляет собой собрание 84 задач прикладного нрава. При решении этих задач выполняются деяния с дробями, рассчитываются площади прямоугольника, треугольника, трапеции и круга, объёмы параллелепипеда, цилиндра, размеры пирамид. Имеются также задачки на пропорциональное деление, а при решении одной задачки находится сумма геометрической прогрессии.

В столичном папирусе собраны решения 25 задач. Большая часть их такового же типа, как и в папирусе Ринда. Не считая того, в одной из задач верно рассчитывается объём усечённой пирамиды с квадратным основанием. В иной задачке содержится самый ранешний в арифметике пример определения площади кривой поверхности: рассчитывается боковая поверхность корзины, т.е. полуцилиндра, высота которого равна поперечнику основания.

При исследовании содержания математических папирусов находится последующий уровень математических познаний старых египтян.

Ко времени написания этих документов уже сложилась определённая система счисления: десятичная иероглифическая. Алгоритмические числа записывались комбинациями узловых чисел. При помощи данной нам системы египтяне управлялись со всеми вычислениями, в каких употребляются целые числа. Что касается дробей, то египтяне сделали особый аппарат, опиравшийся на осознание дроби лишь как толики единицы.

Сложились также определённые приёмы производства математических операций с целыми числами и дробями. Общей для всей вычислительной техники египтян является её аддитивный нрав, при котором все процедуры по способности сводятся к сложению.

При умножении, к примеру, в большей степени употребляется метод постепенного удвоения 1-го из сомножителей и складывания пригодных личных произведений.

При делении также употребляется процедура удвоения и поочередного деления напополам. Деление, по-видимому, было самой трудной математической операцией для египтян. тут наблюдается самое огромное обилие приёмов. Так, время от времени в качестве промежного деяния применялось нахождение 2-ух третей либо одной десятой толики числа и т.п.

При сложении дробей, имеющих различные знаменатели, египтяне употребляли умножение их на вспомогательные числа. методы подбора этих вспомогательных чисел не дают, но, права судить о этом приёме как о единообразном процессе, адекватном способу приведения дробей к общему знаменателю. Исторические реконструкции почти во всем ещё спорны и не доказаны достаточным количеством фактов.

Материалы, находящиеся в папирусах, разрешают утверждать , что за 20 веков до нашей эпохи в Египте начали складываться элементы арифметики как науки. Эти элементы ещё лишь начинают выделяться из практических задач, полностью подчинены их содержанию. техника вычислений ещё примитивна, способы решения задач не единообразны. Но материалов, которые дозволяли бы судить о развитии арифметики в Египте, ещё недостаточно.

Вавилон

Источником наших познаний о вавилонской цивилизации служат отлично сохранившиеся глиняные таблички, покрытые т.н. клинописными текстами, которые датируются от 2000 до н.э. и до 300 н.э. Математика на клинописных табличках в главном была связана с ведением хозяйства. Математика и нехитрая алгебра использовались при обмене средств и расчетах за продукты, вычислении обычных и сложных процентов, налогов и толики урожая, сдаваемой в пользу страны, храма либо землевладельца. Бессчетные арифметические и геометрические задачки появлялись в связи со строительством каналов, зернохранилищ и иными публичными работами. Весьма принципиальной задачей арифметики был расчет календаря, так как календарь употреблялся для определения сроков сельскохозяйственных работ и религиозных праздничков. Деление окружности на 360, а градуса и минутки на 60 частей берут начало в вавилонской астрономии.

Вавилоняне сделали и систему счисления, использовавшую для чисел от 1 до 59 основание 10. знак, обозначавший единицу, повторялся необходимое количество раз для чисел от 1 до 9. Для обозначения чисел от 11 до 59 вавилоняне употребляли комбинацию знака числа 10 и знака единицы. Для обозначения чисел, начиная с 60 и больше, вавилоняне ввели позиционную систему счисления с основанием 60. Значимым продвижением стал позиционный принцип, согласно которому один и этот же числовой символ (знак) имеет разные значения зависимо от того места, где он размещен. Примером могут служить значения шестерки в записи (современной) числа 606. Но ноль в системе счисления старых вавилонян отсутствовал, из – за чего же один и этот же набор знаков мог означать и число 65 (60 + 5), и число 3605 (602 + 0 + 5). Появлялись неоднозначности и в трактовке дробей. к примеру, одни и те же знаки могли означать и число 21, и дробь 21/60 и (20/60 + 1/602). Неоднозначность разрешалась зависимо от определенного контекста.

Вавилоняне составили таблицы оборотных чисел (которые использовались при выполнении деления), таблицы квадратов и квадратных корней, также таблицы кубов и кубических корней. Им было понятно не плохое приближение числа 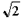. Клинописные тексты, посвященные решению алгебраических и геометрических задач, свидетельствуют о том, что они воспользовались квадратичной формулой для решения квадратных уравнений и могли решать некие особые типы задач, включавших до 10 уравнений с 10 неведомыми, также отдельные разновидности кубических уравнений и уравнений четвертой степени. На глиняных табличках запечатлены лишь задачки и главные шаги процедур их решения. Потому что для обозначения неведомых величин использовалась геометрическая терминология, то и способы решения в главном заключались в геометрических действиях с линиями и площадями. Что касается алгебраических задач, то они формулировались и решались в словесных обозначениях.

Около 700 до н.э. вавилоняне стали использовать арифметику для исследования движений Луны и планет. Это позволило им предвещать положения планет, что было принципиально как для астрологии, так и для астрономии.

В геометрии вавилоняне знали о таковых соотношениях, к примеру, как пропорциональность соответственных сторон схожих треугольников. Им была известна аксиома Пифагора и то, что угол, вписанный в полуокружность – прямой. Они располагали также правилами вычисления площадей обычных плоских фигур, в том числе правильных многоугольников, и размеров обычных тел. Число Пи вавилоняне считали равным 3.

В 1849-1850 гг. в развалинах старого городка Ниневия была найдена древная библиотека. Выяснилось, что практически за 2000 лет до н. э. были составлены таблицы умножения, квадратов поочередных целых чисел. Для решения квадратных уравнений народы Месопотамии разработали систему действий, эквивалентную современной формуле. Но не были найдены рассуждения, приведшие к применяемому методу, т. е. арифметику Старого Вавилона можно было именовать рецептурной, хотя непонятно, каким образом были получены эти рецепты.

Для обозначения чисел вавилоняне воспользовались 2-мя значками: вертикальным и горизонтальным клиньями. Числа от 1 до 9 записывались при помощи соответственного числа вертикальных клиньев; 10 — горизонтальный клин, 60 — опять вертикальный клин. Данную систему недозволено именовать совершенной, потому что одна композиция могла обозначать разные числа.

Следы вавилонской нумерации сохранились до сего времени: 1 час = 60 минут, 1 минутка = 60 секунд; аналогично при делении окружности на градусы, минутки, секунды. Таковая Традиция пришла из астрономии. Вавилоняне проводили периодические наблюдения за звездным небом, составляли календарь, вычисляли периоды воззвания Луны и всех планет, могли предвещать солнечные и лунные затмения. Эти познания астрономии потом перебежали к грекам, которые вкупе с астрономическими таблицами заимствовали и шестидесятеричную нумерацию.

При развитии арифметики сначало формируются понятия «больше», «меньше», «равно», все это тесновато соединено с определенными предметами. Счет предметов производили почаще всего при помощи пальцев. Потому самыми всераспространенными являются десятеричная либо двадцатеричная системы счисления. С возникновением нуля появилась позиционная система счисления

Старая Греция

Исходя из убеждений 20 в. родоначальниками арифметики явились греки традиционного периода (6 – 4 вв. до н.э.). Математика, существовавшая в наиболее ранешний период, была набором эмпирических заключений. Напротив, в дедуктивном рассуждении новое утверждение выводится из принятых посылок методом, исключавшим возможность его неприятия.

Настаивание греков на дедуктивном подтверждении было экстраординарным шагом. Ни одна иная цивилизация не дошла до идеи получения заключений только на базе дедуктивного рассуждения, исходящего из очевидно сформулированных аксиом. Одно из разъяснений приверженности греков способам дедукции мы находим в устройстве греческого общества традиционного периода. Арифметики и философы (часто это были одни и те же лица) принадлежали к высшим слоям общества, где неважно какая практическая деятельность рассматривалась как недостойное занятие. Арифметики предпочитали абстрактные рассуждения о числах и пространственных отношениях решению практических задач. Математика делилась на математику – теоретический нюанс и логистику – вычислительный нюанс. Заниматься логистикой предоставляли свободнорожденным низших классов и рабам.

Греческая система счисления была базирована на использовании букв алфавита. Аттическая система, бывшая в ходу с 6–3 вв. до н.э., употребляла для обозначения единицы вертикальную черту, а для обозначения чисел 5, 10, 100, 1000 и 10 000 исходные буковкы их греческих заглавий. В наиболее поздней ионической системе счисления для обозначения чисел использовались 24 буковкы греческого алфавита и три архаические буковкы. Кратные 1000 до 9000 обозначались так же, как 1-ые девять целых чисел от 1 до 9, но перед каждой буковкой ставилась вертикальная черта.

10-ки тыщ обозначались буковкой М (от греческого «мириои» – 10 000), опосля которой ставилось то число, на которое необходимо было помножить 10 тыщ

Дедуктивный нрав греческой арифметики вполне сформировался ко времени Платона и Аристотеля. Изобретение дедуктивной арифметики принято приписывать Фалесу Милетскому (ок. 640–546 до н.э.), который, как и почти все древнегреческие арифметики традиционного периода, был также философом. Высказывалось предположение, что Фалес употреблял дедукцию для подтверждения неких результатов в геометрии, хотя это непонятно.

Иным величавым греком, с чьим именованием связывают развитие арифметики, был Пифагор (ок. 585–500 до н.э.). Считают, что он мог познакомиться с вавилонской и египетской арифметикой во время собственных длительных странствий. Пифагор основал движение, расцвет которого приходится на период ок. 550–300 до н.э. Пифагорейцы сделали чистую арифметику в форме теории чисел и геометрии. Целые числа они представляли в виде конфигураций из точек либо камешков, классифицируя эти числа в согласовании с формой возникающих фигур («фигурные числа»). слово «калькуляция» (расчет, вычисление) берет начало от греческого слова, значащего «камешек». Числа 3, 6, 10 и т.д. пифагорейцы называли треугольными, потому что соответственное число камешков можно расположить в виде треугольника, числа 4, 9, 16 и т.д. – квадратными, потому что соответственное число камешков можно расположить в виде квадрата, и т.д.

Из обычных геометрических конфигураций появлялись некие характеристики целых чисел. к примеру, пифагорейцы нашли, что сумма 2-ух поочередных треугольных чисел постоянно равна некому квадратному числу. Они открыли, что если (в современных обозначениях) n2
– квадратное число, то n2
+ 2n +1 = (n + 1)2
. Число, равное сумме всех собственных собственных делителей, не считая самого этого числа, пифагорейцы называли совершенным. Примерами совершенных чисел могут служить такие целые числа, как 6, 28 и 496. Два числа пифагорейцы называли дружескими, если каждое из чисел равно сумме делителей другого; к примеру, 220 и 284 – дружеские числа (и тут само число исключается из собственных делителей).

Для пифагорейцев хоть какое число представляло собой нечто большее, чем количественную величину. к примеру, число 2 согласно их мнению означало различие и поэтому отождествлялось с воззрением. Четверка представляла справедливость, потому что это 1-ое число, равное произведению 2-ух схожих множителей.

Пифагорейцы также открыли, что сумма неких пар квадратных чисел есть опять квадратное число. к примеру, сумма 9 и 16 равна 25, а сумма 25 и 144 равна 169. Такие тройки чисел, как 3, 4 и 5 либо 5, 12 и 13, именуются пифагоровыми числами. Они имеют геометрическую интерпретацию, если два числа из тройки приравнять длинам катетов прямоугольного треугольника, то третье число будет равно длине его гипотенузы. Таковая интерпретация, по-видимому, привела пифагорейцев к пониманию наиболее общего факта, известного сейчас под заглавием аксиомы Пифагора, согласно которой в любом прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Рассматривая прямоугольный треугольник с единичными катетами, пифагорейцы нашли, что длина его гипотенузы равна 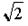, и это повергло их в смятение, ибо они напрасно пробовали представить число 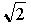в виде дела 2-ух целых чисел, что было очень принципиально для их философии. Величины, непредставимые в виде дела целых чисел, пифагорейцы окрестили несоизмеримыми; современный термин – «иррациональные числа». Около 300 до н.э. Евклид обосновал, что число 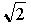несравненно. Пифагорейцы

имели дело с иррациональными числами, представляя все величины геометрическими видами. Если 1 и 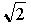считать длинами неких отрезков, то различие меж оптимальными и иррациональными числами сглаживается. Произведение чисел 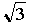и 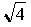есть площадь прямоугольника со сторонами длино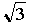й и 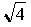.Мы и сейчас время от времени говорим о числе 25 как о квадрате 5, а о числе 27 – как о кубе 3.

Древнейшие греки решали уравнения с неведомыми средством геометрических построений. Были разработаны особые построения для выполнения сложения, вычитания, умножения и деления отрезков, извлечения квадратных корней из длин отрезков; сейчас этот способ именуется геометрической алгеброй.

Приведение задач к геометрическому виду имело ряд принципиальных последствий. А именно, числа стали рассматриваться раздельно от геометрии, так как работать с несоизмеримыми отношениями можно было лишь при помощи геометрических способов. Геометрия стала основой практически всей серьезной арифметики, по последней мере, до 1600 г. И даже в 18 в., когда уже были довольно развиты алгебра и математический анализ, строгая математика трактовалась как геометрия, и слово «геометр» было равнозначно слову «математик».

Конкретно пифагорейцам мы почти во всем должны той арифметикой, которая потом была систематизировано изложена и подтверждена в Началах Евклида. Есть основания считать, что конкретно они открыли то, что сейчас понятно как аксиомы о треугольниках, параллельных прямых, многоугольниках, окружностях, сферах и правильных полиэдрах.

Одним из самых выдающихся пифагорейцев был способ начинается с утверждения, которое требуется обосновать, и потом из него поочередно выводятся следствия до того времени, пока не будет достигнут какой – нибудь узнаваемый факт; подтверждение выходит при помощи оборотной процедуры.) Принято считать, что последователи Платона изобрели способ подтверждения, получивший заглавие «подтверждение от неприятного». Приметное пространство в истории арифметики занимает Аристотель, ученик Платона. способности геометрических построений.

Величайшим из греческих математиков традиционного периода, уступавшим по значимости приобретенных результатов лишь Архимеду, был Евдокс (ок. 408–355 до н.э.). Конкретно он ввел понятие величины для таковых объектов, как отрезки прямых и углы. Располагая понятием величины, Евдокс логически строго доказал пифагорейский способ воззвания с иррациональными числами.

работы Евдокса дозволили установить дедуктивную структуру арифметики на базе очевидно формулируемых аксиом. Ему принадлежит и 1-ый шаг в разработке математического анализа, так как конкретно он изобрел способ вычисления площадей и размеров, получивший заглавие «способа исчерпывания». Этот способ состоит в построении вписанных и обрисованных плоских фигур либо пространственных тел, которые заполняют («исчерпывают») площадь либо размер той фигуры либо того тела, которое является предметом исследования. Евдоксу же принадлежит и 1-ая астрономическая теория, объясняющая наблюдаемое движение планет. Предложенная Евдоксом теория была чисто математической; она демонстрировала, каким образом композиции крутящихся сфер с разными радиусами и осями вращения могут разъяснить кажущиеся нерегулярными движения Солнца, Луны и планет.

Около 300 до н.э. результаты почти всех греческих математиков были сведены в единое целое Евклидом, написавшим математический шедевр “Начала”. Из немногих проницательно отобранных аксиом Евклид вывел около 500 теорем, охвативших все более принципиальные результаты традиционного периода. Свое сочинение Евклид начал с определения таковых определений, как ровная, угол и окружность. Потом он определил 10 самоочевидных истин, таковых, как «целое больше хоть какой из частей». И из этих 10 аксиом Евклид сумел вывести все аксиомы. Для математиков текст Начал Евклида длительное время служил прототипом строгости, пока в 19 в. не обнаружилось, что в нем имеются суровые недочеты, такие как неосознанное внедрение не сформулированных в очевидном виде допущений.

Аполлоний (около 262–200 до н.э.) жил в александрийский период, но его главный труд выдержан в духе традиционных традиций. Предложенный им анализ конических сечений – окружности, эллипса, параболы и гиперболы – явился кульминацией развития греческой геометрии. Аполлоний также стал основоположником количественной математической астрономии.

В течение долгого времени математические сведения не были выделены в отдельную область науки. Принципиальные и достойные внимания астрономические, технические и остальные открытия, наблюдения за явлениями природы, новейшие способы вычислений и решения новейших классов задач стекались в Грецию со всех сторон, распространялись в кругах образованных людей, сливаясь в единую, хотя и слабо сначала объединенную, область всеобщего научного познания. Называли эту область матема ( — познание, наука). Факты данной нам науки заполучили заглавие научных, математических.

Но время шло и равномерно скопление научных сведений беспристрастно вынуждало к тому, чтоб их упорядочить, систематизировать. То же рвение к разделению, дифференциации познаний вырастало из практики школьного обучения. Понятно, что все детки вольных людей рабовладельческих Афин и остальных полисов с семилетнего возраста обучались в школах. Там их учили как дисциплинам практического предназначения, так и начаткам теоретического научного познания, в том числе основам теоретической математики и геометрии. Став взрослыми, они вследствие привилегированного положения в обществе передавали подначальным людям не только лишь физический труд, да и решение практических задач, связанных с необходимостью счета и измерений. Такое разделение математических занятий, возникшее в силу общественного неравноправия людей, ускоряло беспристрастное течение исторического процесса дифференциации научных познаний и выделения слоя людей, занимающихся теоретическими неуввязками арифметики. Этому же содействовало деятельность учебно-научных объединений натурфилософского направления (научных школ). Это были по преимуществу маленькие группы юных людей, собиравшихся вокруг узнаваемых ученых; преподавание велось основным образом устно.

Древнегреческие школы

Элейская школа

Элейская школа достаточно увлекательна для исследования, потому что это одна из древних школ, в трудах которой математика и Философия довольно тесновато и неоднозначно ведут взаимодействие. Главными представителями Элейской школы считают Парменида (конец VI — V в. до н.э.) и Зенона (1-ая половина V в. до н.э.).

Философия Парменида заключается в последующем: различные системы мировоззрения базируются на одной из 3-х посылок: 1) есть лишь бытие, небытия нет; 2) существует не только лишь бытие, да и небытие; 3) бытие и небытие тождественны. Настоящий Парменид признает лишь первую посылку. Согласно ему – бытие едино, неразделимо, неизменяемо, вневременно, закончено внутри себя, лишь оно поистине сущее; множественность, изменчивость, прерывность, текучесть — все это удел надуманного.

С возражением выступил его ученик Зенон. Древнейшие причисляли ему 40 доказательств для защиты учения о единстве сущего (против множественности вещей) и 5 доказательств его неподвижности (против движения). Из их до нас дошло всего девять. Большей известностью во все времена воспользовались зеноновы подтверждения против движения.

Аргументы Зенона приводят к феноминальным, исходя из убеждений «здравого смысла», выводам, но их недозволено было просто откинуть как несостоятельные, так как и по форме, и по содержанию удовлетворяли математическим эталонам той поры. Разложив апории Зенона на составные части и двигаясь от заключений к посылкам, можно реконструировать начальные положения, которые он брал за базу собственной концепции. Принципиально отметить, что в концепции элеатов, как и в дозеноновской науке, фундаментальные философские представления значительно опирались на математические принципы. Видное пространство посреди их занимали последующие теоремы:

1. Сумма нескончаемо огромного числа всех, хотя бы и нескончаемо малых, но протяженных величин обязана быть нескончаемо большенный;

2. Сумма хоть какого, хотя бы и нескончаемо огромного числа непротяженных величин постоянно равна нулю и никогда не может стать некой заблаговременно данной протяженной величиной.

Конкретно в силу тесноватой связи общих философских представлений с базовыми математическими положениями удар, нанесенный Зеноном по философским мнениям, значительно затронул систему математических познаний. Целый ряд важных математических построений, считавшихся ранее, непременно, настоящими, в свете зеноновских построений выглядели как противоречивые. Рассуждения Зенона привели к необходимости переосмыслить более принципиальные методические вопросцы.

Милетская школа

Милетская школа – одна из первых древнегреческих математических школ, оказавшая существенное воздействие на развитие философских представлений того времени. Она была в Ионии в конце V — IV вв. до н.э.; главными деятелями ее являлись Фалес (около 624-547 гг. до н.э.), Анаксимандр (около. 610-546 гг. до н.э.) и Анаксимен (около 585-525 гг. до н.э.). Разглядим на примере милетской школы главные отличия греческой науки от догреческой и проанализируем их. Если сравнить начальные математические познания греков с достижениями египтян и вавилонян, то навряд ли можно колебаться в том, что такие простые положения, как равенство углов у основания равнобедренного треугольника, открытие которого приписывают Фалесу Милетскому, не были известны старой арифметике. Тем не наименее, греческая математика уже в начальном собственном пт имела высококачественное отличие от собственных предшественников. Ее своеобразие заключается, до этого всего, в попытке систематически применять идею подтверждения. Фалес стремится обосновать то, что эмпирически было получено и без подабающего обоснования использовалось в египетской и вавилонской арифметике. Может быть, в период более интенсивного развития духовной жизни Вавилона и Египта, в период формирования основ их познаний, изложение тех либо других математических положений сопровождалось обоснованием в той либо другой форме.

Но, как пишет Ван дер Варден, «во времена Фалеса египетская и вавилонская математика издавна уже были мертвыми познаниями. Можно было показать Фалесу, как следует вычислять, но уже неизвестен был ход рассуждений, лежащих в базе этих правил». Греки вводят процесс обоснования как нужный компонент математической реальности – доказательность, которая вправду рассматриваемого положения, уверенность в силе людского являлась отличительной чертой их арифметики. Техникой подтверждения ранешней греческой арифметики, как в геометрии, так и в математике, сначало являлась обычная попытка придания наглядности. Определенными разновидностями такового подтверждения в математике было подтверждение с помощью камешков, в геометрии — методом наложения. Но сам факт наличия подтверждения гласит о том, что математические познания воспринимаются не догматически, а в процессе размышления. Это, в свою очередь, обнаруживает критичный склад мозга, уверенность (быть может, не постоянно осознанную), что размышлением можно установить корректность либо ложность Греки в течение 1-го – 2-ух веков смогли завладеть математическим наследием предшественников, скопленного в течении 1000-летий, что свидетельствует о интенсивности, динамизме их математического зания. Высококачественное отличие исследовательских работ Фалеса и его последователей от догреческой арифметики проявляется не столько в определенном содержании исследованной зависимости, сколько в новеньком методе математического мышления. Начальный материал греки взяли у предшественников, но метод усвоения и использования этого материала был новейший. Различительными чертами их математического зания являются рационализм, критицизм, динамизм. Эти же черты свойственны и для философских исследовательских работ милетской школы.

Индия и Арабы

Преемниками греков в истории арифметики стали индийцы. Индийские арифметики не занимались подтверждениями, но они ввели уникальные понятия и ряд действенных способов. Конкретно они в первый раз ввели нуль и как кардинальное число, и как знак отсутствия единиц в соответственном разряде. Махавира (850 н.э.) установил правила операций с нулем, полагая, но, что деление числа на нуль оставляет число постоянным. Верный ответ для варианта деления числа на нуль был дан Бхаскарой (р. в 1114), ему принадлежат правила действий над иррациональными числами. Индийцы ввели понятие отрицательных чисел (для обозначения долгов). Самое преждевременное их внедрение мы находим у Брахмагупты (ок. 630). Ариабхата (р. 476) начал двигаться далее Диофанта в использовании непрерывных дробей при решении неопределенных уравнений.

Наша современная система счисления, основанная на позиционном принципе записи чисел и нуля как кардинального числа и использовании обозначения пустого разряда, именуется индо – арабской. На стенке храма, построенного в Индии около 250 до н.э., найдено несколько цифр, напоминающих по своим очертаниям наши современные числа.

Около 800 индийская математика достигнула Багдада. термин «алгебра» происходит от начала наименования книжки Аль-джебр вал – мукабала (Восполнение и противопоставление), написанной в 830 астрологом и математиком аль-Хорезми. В собственном сочинении он воздавал подабающее заслугам индийской арифметики. Алгебра аль-Хорезми была базирована на трудах Брахмагупты, но в ней явственно различимы вавилонское и греческое воздействия. иной выдающийся арабский математик Ибн аль – Хайсам (около 965–1039) разработал метод получения алгебраических решений квадратных и кубических уравнений. Арабские арифметики, в числе их и Омар Хайям, умели решать некие кубические уравнения при помощи геометрических способов, используя конические сечения. Арабские астрологи ввели в тригонометрию понятие тангенса и котангенса. Насирэддин Туси (1201–1274) в Трактате о полном четырехугольнике систематически выложил плоскую и сферическую геометрии и первым разглядел тригонометрию раздельно от астрономии.

Средние Века и Возрождение

Средневековая Европа. Римская цивилизация не оставила приметного следа в арифметике, так как была очень озабочена решением практических заморочек. Цивилизация, сложившаяся в Европе ранешнего Средневековья (около 400–1100), не была продуктивной по прямо обратной причине: умственная жизнь сосредоточилась практически только на теологии и загробной жизни. Уровень математического познания не поднимался выше математики и обычных разделов из Начал Евклида. Более принципиальным разделом арифметики в Средние века числилась астрология; астрономов называли математиками. А так как мед практика основывалась в большей степени на астрологических показаниях либо противопоказаниях, докторам не оставалось ничего другого, как стать математиками.

Около 1100 в западноевропейской арифметике начался практически трехвековой период освоения сохраненного арабами и византийскими греками наследства Старого мира и Востока. Так как арабы обладали практически всеми трудами старых греков, Европа получила необъятную математическую литературу. Перевод этих трудов на латынь содействовал подъему математических исследовательских работ. Все величавые ученые того времени признавали, что черпали вдохновение в трудах греков.

Первым заслуживающим упоминания европейским математиком стал Леонардо Пизанский (Фибоначчи). В собственном сочинении Книжка абака (1202) он познакомил европейцев с индо – арабскими цифрами и способами вычислений, также с арабской алгеброй. В течение последующих нескольких веков математическая активность в Европе ослабела. Свод математических познаний той эры, составленный Лукой Пачоли в 1494, не содержал каких-то алгебраических новшеств, которых не было у Леонардо.

Возрождение. Посреди наилучших геометров эры Возрождения были живописцы, развившие идею перспективы, которая добивалась геометрии со сходящимися параллельными прямыми. Живописец Леон Баттиста Альберти (1404–1472) ввел понятия проекции и сечения. Прямолинейные лучи света от глаза наблюдающего к разным точкам изображаемой сцены образуют проекцию; сечение выходит при прохождении плоскости через проекцию. Чтоб нарисованная картина смотрелась реалистической, она обязана была быть таковым сечением. Понятия проекции и сечения порождали чисто математические вопросцы. к примеру, какими общими геометрическими качествами владеют сечение и начальная сцена, каковы характеристики 2-ух разных сечений одной и той же проекции, образованных 2-мя разными плоскостями, пересекающими проекцию под разными углами? Из таковых вопросцев и появилась проективная геометрия. Ее основоположник – Ж.Дезарг (1593–1662) при помощи доказательств, основанных на проекции и сечении, унифицировал подход к разным типам конических сечений, которые величавый греческий геометр Аполлоний разглядывал раздельно.

Старая Русь

Почти все и по сию пору убеждены, что в допетровскую эру на Руси совершенно ничему не учили. Наиболее того, само образование тогда типо преследовала церковь, требовавшая лишь, чтоб ученики кое-как говорили назубок молитвы и понемногу разбирали печатные богослужебные книжки. Ну и учили, дескать, только деток поповских, готовя их к принятию сана. Те же из знати, кто веровал в истин «учение — свет…», поручали образование собственных отпрысков выписанным из-за границы иноземцам. Другие же обретались «во тьме неведения».

Все это опровергает Мордовцев. В собственных исследовательских работах он опирался на любознательный исторический источник, попавший к нему в руки, — «Азбуковник». В вступлении к монографии, посвященной данной нам рукописи, создатель написал последующее: «В истинное время я имею возможность воспользоваться драгоценнейшими монументами 17 – го века, которые еще нигде не были написаны, не упомянуты и которые могут послужить к разъяснению увлекательных сторон старой российской педагогики. Материалы эти заключаются в обширной рукописи, носящей заглавие «Азбуковника» и вмещающей в себя несколько различных учебников тех пор, сочиненных каким-то «первопроходчиком», частично списанных с остальных, таковых же, изданий, которые озаглавлены, были этим же именованием, хотя и различались содержанием и имели разный счет листов».

Изучив рукопись, Мордовцев делает 1-ый и важный вывод: в Старой Руси училища как таковые существовали. Вообщем, подтверждает это и наиболее старый документ — книжка «Стоглав» (собрание постановлений Стоглавого Собора, проходившего с ролью Ивана IV и представителей Боярской думы в 1550 – 1551 годах). В ней содержатся разделы, говорящие о образовании. В их, а именно, определено, что училища разрешено содержать лицам духовного звания, если соискатель получит на то разрешение у церковного начальства. Перед тем, как выдать ему таковое, надлежало провести тесты основательности собственных знаний претендента, а от надежных поручителей собрать вероятные сведения о его поведении.

Но как были устроены училища, как управлялись, кто в их учился? На эти вопросцы «Стоглав» ответов не давал. И вот в руки историка попадает несколько рукописных «Азбуковников» — книжек очень любознательных. Невзирая на свое заглавие, это, на самом деле, не учебники (в их нет ни азбуки, ни прописей, ни обучения счету), а быстрее управление для учителя и подробнейшие наставления ученикам. В нем прописан полный распорядок денька школяра, к слову, касающийся не только лишь школы, да и поведения деток за ее пределами.

Из «Азбуковника» мы узнаем весьма принципиальный факт: образование в описываемые времена не было на Руси сословной преимуществом. В рукописи, от лица «Мудрости», содержится призыв к родителям различных сословий отдавать отроков для обучения «прехитрой словесности»: «Этого ради присно глаголю и глаголя не престану людям благочестивым во слышание, всякого чина же и сана, славным и худородным, богатым и убогим, даже и до крайних хлеборобов». Ограничением к обучению служили только нежелание родителей или уж совершеннейшая их бедность, не позволявшая хоть чем-нибудь произвести оплату учителю за обучение чада.

Но последуем за учеником, вошедшим в училище и уже положившим свою шапку на «общую грядку», другими словами на полку, поклонившимся и образам, и учителю, и всей ученической «дружине». Школяру, пришедшему в школу ранешным с утра, предстояло провести в ней целый денек, до гула к вечерней службе, который был сигналом и к окончанию занятий.

учение начиналось с ответа урока, изучавшегося намедни. Когда же урок был всеми рассказан, вся «дружина» совершала перед последующими занятиями общую молитву: «Господи, Иисусе Христе, Боже наш, содетелю всякой твари, вразуми мя и обучи книжного писания и сим увем хотения Твоя, яко да славлю Тя во веки веков, аминь!». Потом ученики подступали к старосте, выдававшему им книжки, по которым предстояло обучаться, и рассаживались за общим длинноватым ученическим столом. Любой занимал пространство, обозначенное ему учителем, соблюдая при всем этом последующие наставления:

Малии в вас и велицыи все равны,

Учений же ради вящих местом да будут знатны…

Не потесняй близкого твоего

И не именуй прозвищем товарища собственного…

Тесновато друг к другу не сочитайтеся,

Коленями и локтями не присвояйтеся…

книжки, будучи собственностью школы, составляли главную ее Ценность. Отношение к книжке внушалось трепетное и почтительное. Требовалось, чтоб ученики, «замкнув книжку», постоянно клали ее печатью наверх и не оставляли в ней «указательных древец» (указок), не очень разгибали и не листали попусту. Категорически запрещалось класть книжки на лавку, а по окончании учения книжки надлежало дать старосте, который складывал их в назначенное пространство. И очередной совет – не увлекаться разглядыванием книжных украшений – «повалок», а стремиться осознать написанное в их

Совершенно дисциплина в древнерусской школе была крепкая, грозная. Весь денек верно расписан правилами, даже пить воду позволялось лишь три раза в денек, а «ради нужды на двор отходити» можно было с разрешения старосты считанные разы

Все «Азбуковники» имели широкий раздел – о наказаниях ленивых, недобросовестных и супротивных учеников с описанием самых различных форм и способов действия. Не случаем «Азбуковники» начинаются панегириком розге, писанным киноварью на первом листе:

Благослови, Боже, оные леса,

Иже розги родят на долгие времена…

Не необходимо, но, мыслить, что ту учение качественной поркой не заменишь. Тому, кто прославился как истязатель да еще плохо учащий, никто бы не отдал собственных деток в учение. Прирожденная беспощадность (если такая имеется) не проявляется в человеке в один момент, и патологически беспощадной личности никто не дозволил бы открыть училище. О том, как надо учить деток, говорилось и в Уложении Стоглавого Собора, бывшем, на самом деле, управлением для учителей: «не яростью, не беспощадностью, не гневом, но веселым ужасом и любовным обычаем, и сладким назиданием, и нежным утешением»

Итак, огромную часть денька ученики неотлучно находились в школе. Для того чтоб иметь возможность отдохнуть либо отлучиться по нужным делам, учитель избирал для себя из учеников ассистента, именуемого старостой. Роль старосты во внутренней жизни тогдашней школы была очень принципиальна. Опосля учителя предводитель был вторым человеком в школе, ему даже дозволялось замещать самого учителя. Потому выбор старосты и для ученической «дружины», и для учителя было делом важным. «Азбуковник» предписывал выбирать таких самому учителю из старших учеников, в учебе прилежных и подходящих духовных свойств. Учителя книжка наставляла: «Имей у себя в остерегании их (другими словами старост. — В.Я.). Наидобрейших и качественных учеников, способных и без для тебя оглашати их (учеников. — В.Я.) пастушеским словом».

О количестве старост говорится по-разному. Быстрее всего, их было трое: один предводитель и два его подручных, так как круг обязательств «избранных» был необыкновенно широкий. Они следили за ходом учебы в отсутствие учителя и даже имели Право наказывать виноватых за нарушение порядка, установленного в школе. Слушали уроки младших школьников, собирали и выдавали книжки, наблюдали за их сохранностью и подабающим с ними воззванием. Ведали «отпуском на двор» и питьем воды. В конце концов, распоряжались отоплением, освещением и уборкой школы. Предводитель и его подручные представляли учителя в его отсутствие, а при нем – доверенных помощников.

Все управление школой старосты проводили без всякого доносительства учителю. По последней мере, так считал Мордовцев, не обнаружив в «Азбуковниках» ни одной строки, поощрявшей фискальство и наушничество. Напротив, учеников всячески приучивали к приятельству, жизни в «дружине». Если же учитель, находясь в поиске провинившегося, не мог буквально указать на определенного ученика, а «дружина» его не выдавала, тогда объявлялось наказание всем ученикам, и они скандировали хором:

В неких из нас есть вина,

Которая не перед почти всеми дньми была,

Виновни, слышав сие, лицом рдятся,

Понеже они нами, кроткими, гордятся.

Нередко виновник, чтобы не подводить «дружину», снимал порты и сам «всходил на козла», другими словами ложился на лавку, на которой и выполнялось «задавание лозанов по филейным частям».

Стоит гласить, что и учение, и воспитание отроков были тогда проникнуты глубочайшим уважением к православной вере. Что смолоду вложено, то и произрастет во взрослом человеке: «Се бо есть ваше детское, в школе учащихся дело, паче же совершенных в возрасте». Ученики были должны ходить в церковь не только лишь в торжественные и воскресные деньки, да и в будни, опосля окончания занятий в училище.

Вечерний благовест давал символ к окончанию учения. «Азбуковник» учит: «Егда отпущены будите, вси купно воссташе и книжки своя книгохранителю вдаваше, единым возглашением всем купно и единодушно воспевайте молитву преподобного Симеона Богоприимца: «Сейчас отпущаеши раба Твоего, Владыко» и «Преславная Приснодево». Опосля этого ученики должны были идти к вечерне, учитель же наставлял их, чтобы в церкви вели себя прилично, поэтому что «все знают, что вы обучайтесь в школе».

Но требования прилично вести себя не ограничивались лишь школой либо храмом. Училищные правила распространялись и на улицу: «Егда же учитель отпустит вас в схожее время, со всем смирением до дому собственного идите: шуток и кощунств, пхания же друг друга, и биения, и быстрого бегания, и камневержения, и всяких схожих детских глумлений, да не водворится в вас». Не поощрялось и бесцельное шатание по улицам, в особенности около всяческих «зрелищных заведений», именуемых тогда «позорищами».

естественно же приведенные правила – наиболее благие пожелания. Нет в природе таковых деток, что удержались бы от «пхания и быстрого бегания», от «камневержения» и похода «на позорище» опосля того, как они целый денек провели в школе. Соображали это в старину и учителя и поэтому стремились всеми мерами уменьшить время безпризорного пребывания учеников на улице, толкающей их к соблазнам и к шалостям. Не только лишь в будние деньки, но в воскресные и в торжественные школяры должны были приходить в училище. правда, в празднички уже не обучались, а лишь отвечали выученное намедни, читали вслух Евангелие, слушали назидания и объяснения учителя собственного о сущности праздничка того денька. Позже все вкупе шли в церковь к литургии.

Интересно отношение к тем ученикам, у каких учение шло плохо. В этом случае «Азбуковник» никак не рекомендует их усиленно пороть либо наказывать как – то по другому, а, напротив, наставляет: «кто «борзоучащийся», да не возносится над товарищем «грубоучащимся». Крайним настоятельно советовалось молиться, призывая на помощь Бога. А учитель с таковыми учениками занимался раздельно, говоря им повсевременно о полезности молитвы и приводя примеры «от писания», рассказывая о таковых подвижниках благочестия, как Сергий Радонежский и Александр Свирский, которым учение сначала совершенно не давалось.

Из «Азбуковника» видны подробности учительской жизни, тонкости отношений с родителями учеников, вносившими учителю по договоренности и по способности всякого плату за обучение собственных детей – частью натурой, частью средствами.

Кроме школьных правил и порядков «Азбуковник» ведает о том, как опосля прохождения начального образования ученики приступают к исследованию «7 вольных художеств». Под коими предполагались: грамматика, Диалектика, риторика, музыка (имелось в виду церковное пение), математика и геометрия («геометрией» тогда именовалось «всякое землемерие», включавшее в себя и географию и космогонию), в конце концов, «крайней по счету, но первой действом» в списке наук, изучавшихся тогда, называлась астрономия (либо по-славянски «звездознание»).

А еще в училищах занимались исследованием стихотворного искусства, силлогизмов, изучали целебры, познание которых числилось нужным для «виршеслогательства», знакомились с «рифмом» из сочинений Симеона Полоцкого, узнавали стихотворные меры – «един и 10 родов стиха». Обучались придумывать двустишия и сентенции, писать приветствия в стихах и в прозе.

К огорчению, труд Даниила Лукича Мордовцева остался неоконченным, его монография была завершена фразой: «На деньках перевели Преосвященного Афанасия в Астраханскую Епархию, лишив меня способности совсем разобрать увлекательную рукопись, и поэтому, не имея под рукою «Азбуковников», и принужден я окончить свою статью тем, на чем тормознул. Саратов 1856 год».

И тем не наименее уже через год опосля того, как работа Мордовцева была написана в журнальчике, его монографию с этим же заглавием издал Столичный институт. талант Даниила Лукича Мордовцева и множественность тем, затронутых в источниках, послуживших для написания монографии, сейчас разрешают нам, мало «домысливая ту жизнь», совершить интересное и не без полезности путешествие «против потока времени» в семнадцатый век.

Даниил Лукич Мордовцев (1830 – 1905), закончив гимназию в Саратове, обучался поначалу в Казанском, потом в Санкт – Петербургском институте, который закончил в 1854 году по историко-филологическому факультету. В Саратове же он начал литературную деятельность. Выпустил несколько исторических монографий, размещенных в «Российском слове», «Российском вестнике», «Вестнике Европы». Монографии направили на себя внимание, и Мордовцеву дают даже занять кафедру истории в Санкт – Петербургском институте. Не наименее был известен Даниил Лукич и как писатель на исторические темы.

От епископа Саратовского Афанасия Дроздова он получает рукописные тетради XVII века, повествующие о том, как были организованы училища на Руси

1-ый учебник арифметики в Рф был написан в дальнем 1703 году Леонтием Филипповичем Магницким. Именовался он «Математика, сиречь наука числительная».

Попытайтесь решить всего одну задачу из этого учебника:

«отец привел в училище собственного отпрыска и задал вопрос учителя:

-Скажи мне, сколько у тебя учеников?

Учитель дал ответ:

-Если учеников придет столько, сколько я уже имею, да еще полстолька, да еще 4-ая часть, да еще твой отпрыск, тогда у меня будет 100.

сколько же учеников было в училище?»

Магницкий, Леонтий Филиппович – математик (1669 — 1739). Обучался в Столичной славяно – Греко – латинской академии; потом без помощи других исследовал математические науки, в объеме, далековато превосходящем уровень сведений, сообщаемых

в российских арифметических, землемерных и астрономических рукописях XVII столетия. Опосля открытия в Москве (1701) школы «математических и навигацких наук» назначен туда педагогом математики и, по всей вероятности, геометрии и тригонометрии. Составил учебную энциклопедию по арифметике под заглавием «Математика, сиречь наука числительная» и т. д. (1703), содержащую обширное изложение математики, важные для практических приложений статьи простой алгебры, приложения математики и алгебры к геометрии, практическую геометрию, понятия о вычислении тригонометрических таблиц и о тригонометрических вычислениях совершенно и необходимейшие исходные сведения из астрономии, геодезии и навигации (сейчас выходит новое издание данной нам Математики; выпуск 1, Москва, 1914, с вступлением П. Баранова). Как учебник, эта книжка наиболее полвека употреблялась в школах. Позже Магницкий участвовал в первом российском издании логарифмических таблиц А. Влакка. Правительство Петра Величавого недостаточно ценило награды Магницкого и ставило его, как педагога, ниже его товарищей-англичан, Фарварсона и Гвина. Он получал существенно наименьшее жалованье, и, когда его товарищи были переведены в Петербург, в открывшуюся там морскую академию (1715), он остался в Москве на прежней должности в школе, занявшей по отношению ко вновь открытой академии второстепенное положение (См. Бобынин «Очерки истории развития физико – математических познаний в Рф» («Физико-математические науки в их реальном и прошедшем», тома VII и VIII); Галанин «Магницкий и его математика» (Москва, 1914, 2 – ой выпуск).

Вывод

Исходя из вышесказанного, можно представить, что учебники арифметики, такие, какие мы привыкли созидать на данный момент, возникли сравнимо не так давно. Предпосылкой тому является незаинтересованность самого населения в исследовании наук. Опосля неких технических открытий и конфигурации критерий жизни, учение сделалось первой необходимостью, без которого человек фактически не мог существовать.

Как мы лицезреем, 1-ый учебник по арифметике в Росси возник сначала XVIII века. Другими словами любой человек уже мог, хотя бы без помощи других, но учить эту науку.

В Старой Греции тоже существовали школы, а означает, детки уже тогда могли учить арифметику. Но, потому что в то время существовал рабовладельческий строй, потому это было доступно лишь избранным.

В 17, 18 веках появилась Потребность не только лишь в рабочей силе, да и в приготовленных, ученых людях. Благодаря этому пришлось вводить таковой термин, как образование.

Нынешние учебники очень поменялись по сопоставлению с учебными пособиями того времени. Книжки стали не источником инфы собранной в кучу, а методически распределенным пособием, в каком все хорошо обдуманно с таковым расчетом, чтоб ученик не попросту запомнил формулы и аксиомы, а мог без помощи других, без чьей-то помощи, начав курс арифметики с простого вычисление, через некое время применить свои познания к наиболее сложным задачкам.

Но, если посмотреть на ход истории, то станет понятно, что население земли не обязано тормознуть на этом. С каждым деньком наша жизнь становится все наиболее зависимой от чисел, что просит от нас наивысшей точности, а ошибки стают недопустимыми. Как следует, должны покажется новейшие, наиболее современные способы обучения.

Ссылаясь на то, что комп стал ассистентом человека практически во всех отраслях, можно представить, что конкретно он и поменяет книжки, и обучение будет вестись только с внедрением компьютерных программ.

естественно во всех способах есть свои плюсы и минусы. Мы решили узнать, какие достоинства имеет комп перед учебником. Для этого мы опросили некое количество людей и задали им последующие вопросцы:

Как, по вашему воззрению, поменяются учебники арифметики в дальнейшем?

Учебники поменяют компьютерные программки – 54%

Учебники будут намного труднее – 32%

Учебники будут наиболее тонкими, т.к. в их будет содержаться лишь самая нужная информация – 10%

Учебники будут написаны на наиболее доступном для учеников языке – 4%

Сумеют ли компы поменять учебники?

Да, сумеют – 82%

Нет, не сумеют – 18%

Вроде бы вы желали учить арифметику?

По учебникам – 33%

При помощи компьютерных программ – 67%

Нами было опрошено 50 учеников нашей школы, с 8 по 11 класс.

Опосля проведенного нами опроса, нам сделалось ясно, что будущее все таки за новыми технологиями. Хоть, на данный момент, компы и уступают учебникам в удобстве и простоте обучение , но быстрое развитие технического и информационного прогресса дозволяет считать, что это остается только вопросцем времени…

Перечень литературы

Кудрявский Д.Н. Грихьясутры как источник для истории индоевропейской бытовой культуры. – В кн.: Жива старина, т. 6, вып. 1, 1896

Кудрявский Д.Н. Прием знатного гостя по древнеиндийским правилам домашнего обряда. – Журн. Мин-ва нар. просвещения, 1896, ч. 305, № 5, отд. 2

Кудрявский Д.Н. Исследования в области древне-индийских домашних обрядов. Юрьев, 1904

Семенцов В.С. Трудности интерпретации брахманической прозы. Ритуальный символизм. М., 1981

Пандей Р.Б. Древнеиндийские домашние ритуалы. М., 1982

«Домашние ритуалы». Ашвалаяна-грихьясутра. – В кн.: История и истории арифметики. М., 1986

Клейн Ф. Лекции о развитии арифметики в XIX столетии. М., 1989

Рыбников К.А. История арифметики 1917г. М., 1974

Юшкевич А.П. История арифметики в Рф до 1917г. М., 1968

]]>