Учебная работа. Реферат: Теория Рамсея
Рональд Л. Грэм, Джоуэл X. Спенсер
Как повествует написанный три с половиной тыщи лет вспять клинописный текст, в один прекрасный момент древнешумерский учёный посмотрел на звёздное небо и узрел льва, буйвола и скорпиона. Современный астролог быстрее всего склонен обрисовывать созвездие как временную группу звёзд, которую мы, земляне, смотрим с одной точки на краю обыкновенной галактики. И всё же большая часть любителей поглазеть на звёзды согласятся, что ночное небо смотрится сплошь испещренным созвездиями, имеющими форму прямых линий, четырёхугольников и пятиугольников. Может ли так быть, что подобные геометрические фигуры порождаются какими-то неведомыми нам силами, действующими во Вселенной?
Математика дает куда наиболее обычное разъяснение. В 1928году Фрэнк Пламптон Рамсей, британский математик, философ и экономист, обосновал, что такие упорядоченные конфигурации безизбежно находятся в хоть какой большенный структуре, будь то группа звёзд, совокупа случаем разбросанных камешков либо последовательность чисел, приобретенных бросанием игральной кости. Если речь идёт о довольно большенном количестве звёзд, то постоянно можно отыскать группу, которая с весьма большенный точностью образует какую-нибудь заданную конфигурацию: прямую линию, прямоугольник либо, если уж мы заговорили о звёздах, большенный ковш. Практически теория Рамсея утверждает, что неважно какая структура непременно содержит упорядоченную подструктуру. Как в первый раз назначил около четверти века вспять погибший не так давно южноамериканский математик Теодор С.Моцкин, из теории Рамсея следует, что полный кавардак неосуществим.
Спецы по теории Рамсея стараются вычислить, сколь велико обязано быть огромное количество звёзд, чисел либо каких-то объектов, чтоб можно было гарантировать существование определённой хотимой подструктуры. На решение таковых задач нередко требуются десятилетия, и поддаются они лишь при самом изобретательном и узком рассуждении. Пытаясь отыскать решения поставленной задачки, спецы по теории Рамсея помогают тем инженерам в построении наиболее совершенных сетей коммуникации и систем передачи и поиска инфы. Они также открыли некие математические способы, которые понадобятся учёным последующего столетия. Может быть, самое принципиальное состоит в том, что теория Рамсея изучит основополагающую структуру арифметики, т.е. структуру, пронизывающую всю Вселенную.
В отличие от почти всех разделов современной арифметики теорию Рамсея можно выложить на интуитивном уровне. По правде, привлекательность данной теории частично обоснована той простотой, с которой можно сконструировать её задачки. К примеру, если из присутствующих на вечеринке случайным образом избрать 6 человек (скажем, Альфреда, Бетти, Кэлвина, Дебору, Эдварда и Фрэнсис), то правильно ли, что или трое из их друг с другом знакомы, или трое из их незнакомы друг с другом?
Мы можем решить эту «головоломку о вечеринке» почти всеми методами. Мы могли бы перебрать все мыслимые композиции и проверить, содержит ли любая рассматриваемая группа трёх знакомых либо трёх незнакомых людей. Но так как нам пришлось бы проверить 32768 (либо 215
) композиций, то таковой «способ грубой силы» не является ни удобным, ни менторским.
К Счастью, мы можем найти ответ, рассмотрев два обычных варианта. В первом из их представим, что Альфред понимает трёх (либо больше) из числа других гостей, скажем, Бетти, Кэлвина и Дебору. Если Бетти и Кэлвин, либо Бетти и Дебора, либо Кэлвин и Дебора знакомы друг с другом, то Альфред и пара знакомых образуют группу из трёх знакомых людей; в неприятном случае Бетти, Кэлвин и Дебора друг с другом незнакомы. Во 2-м случае представим, что Альфред понимает самое большее 2-ух (либо меньше) из гостей, скажем, Бетти и Кэлвина. Если Дебора и Эдвард, либо Дебора и Фрэнсис, либо Эдвард и Фрэнсис незнакомы друг с другом, то Альфред и пара незнакомых меж собой гостей образуют группу из трёх человек, незнакомых вместе. В неприятном случае Дебора, Эдвард и Фрэнсис друг с другом знакомы. Всего в 6 предложениях мы обосновали, почему неважно какая группа из 6 человек обязана включать либо трёх знакомых, либо трёх незнакомых людей. Короче говоря, решение «головоломки о вечеринке» есть личный вариант теории Рамсея.

Рис.1. Головоломка о вечеринке представляет собой задачку, типичную для приложений теории Рамсея. Какое количество людей довольно для того, чтоб образовать группу, в какой постоянно окажется или четыре людей знакомых вместе, или четыре, друг с другом незнакомых? На этом рисунке гости представлены точками. Каждое красноватое ребро на этом графе соединяет гостей, знакомых друг с другом, а каждое голубое — незнакомых. В группе из 17 точек, изображённых на рисунке, нереально отыскать четыре точки для которых сеть соединяющих их рёбер была бы полностью красноватой либо полностью голубой Потому требуется наиболее 17 человек, чтоб посреди их непременно оказалось или четыре знакомых, или четыре незнакомых друг с другом. По сути во всякой группе из 18 человек постоянно найдутся или четыре знакомых, или четыре незнакомых друг с другом.
Обобщая этот личный вариант, мы можем сконструировать аксиому в её полном виде. Заместо 6 человек, как в данной задачке, мы можем взять хоть какое число людей либо, если желаете, хоть какое число объектов. Не считая того, нет нужды ограничиваться 2-мя типами отношений, знакомства и незнакомства. Мы можем взять хоть какое число взаимоисключающих отношений — к примеру друзья, неприятели и соблюдающие нейтралитет.
Теорию Рамсея можно сконструировать в ещё наиболее общем виде. Если число объектов в совокупы довольно велико и любые два объекта связывает одно из набора отношений, то постоянно существует подмножество данной совокупы, содержащее данное число объектов, и при всем этом такое, что в нём все объекты соединены отношением 1-го типа.
Фрэнк Рамсей, в первый раз доказавший это утверждение в 1928году, вырос в Кембридже (Великобритания). Его отец, Артур С.Рамсей, был доктором арифметики и президентом института Магдалины Кембриджского института. В 1925году юный Рамсей, общепризнанный самым наилучшим студентом в области арифметики, закончил институт. Хотя больше всего его заинтересовывали Философия и математическая логика, он также писал работы по экономике, теории вероятности, принятию решений, когнитивной психологии и семантике.
Скоро опосля окончания института он вошёл в группу экономистов, которую возглавлял Джон Мэйнард Кейнс. Рамсей написал только две статьи по математической экономике, но обе до сего времени обширно цитируются. Что касается философии, то его побуждали идеи Джорджа И.Мура, Людвига Витгенштейна и Бертрана Рассела. Мур писал: «Он необыкновенно ясно мыслил: никто не мог легче его избежать тех логических погрешностей, от которых несвободны даже наилучшие философы». Потом произошла катастрофа: в 1930году Рамсей захворал и в 26лет погиб от осложнений опосля операции.
Есть некоторая драматичность в том, каким образом за два года до погибели Рамсей вывел теорию, сейчас именуемую его именованием. Он пришел к главный идее, пытаясь обосновать тезис, выдвинутый Расселом и Альфредом Нортом Уайтхедом в их основополагающем труде «Principia Mathematica» (Базы арифметики). Они представили, что все математические правды могут быть выведены из ограниченного набора аксиом. Развивая эту идею, германский математик Давид Гильберт представил, что обязана существовать процедура, позволяющая решить, следует ли то либо другое утверждение из данного набора аксиом либо нет. Рамсей показал, что в неком личном случае таковая процедура принятия решения существует. (Спустя несколько лет Курт Гёдель и его последователи, британец Алан Тьюринг и остальные, исчерпающим образом обосновали, что в общем случае таковой процедуры не существует.)
Рамсей обосновал свою аксиому в качестве первого шага, пытаясь показать справедливость тезиса Рассела в особом случае. Как оказывается, он мог бы выполнить эту задачку иными средствами. Ранее Рамсей обосновал аксиому, не имеющую дела к тезису, который он доказал и который он никогда бы не сумел обосновать в общем случае.
Так обстояли дела до 1933года, когда два венгерских математика, Пауль Эрдёш и Джордж Шекереш, поновой открыли теорию Рамсея. В главном благодаря их усилиям эта теория стала пользующейся популярностью в среде математиков. В то время Эрдёш был девятнадцатилетним студентом Будапештского института, а Шекереш незадолго ранее получил диплом инженера-химика в Будапештском политехническом институте. совместно с группой друзей-студентов они практически каждое воскресенье встречались в пригородном парке, в главном для дискуссий о арифметике.
В зимнюю пору 1933года одна из студенток, Эстер Клейн, предложила друзьям решить любопытную задачку; обосновать, что если 5 точек на плоскости размещены таковым образом, что никакие три точки не лежат на одной прямой, то непременно найдутся четыре из их, образующие выпуклый четырёхугольник. (К выпуклым фигурам относится, скажем, верный шестиугольник, но не относится пятиконечная звезда. Наиболее строго, многоугольник именуется выпуклым, если всякий отрезок, соединяющий его верхушки, лежит снутри этого многоугольника.)
Позволив друзьям вволю поразмышлять над данной задачей, Клейн представила подтверждение (см. рис.3).
1-Й СЛУЧАЙ
2-Й СЛУЧАЙ
3-Й СЛУЧАЙ
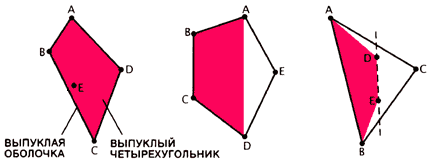
Рис.3. Теория Рамсея была поновой открыта в 1933году, когда юная студентка Эстер Клейн предложила последующую геометрическую задачку: обосновать, что если 5 точек размещены на плоскости и никакие три из их не лежат на одной прямой, то какие-нибудь четыре из их постоянно образуют выпуклый четырёхугольник. Неважно какая конфигурация, удовлетворяющая условиям задачки, относится к одному из трёх случаев, показанных на рисунке. Простой вариант — тот, когда выпуклая оболочка (т.е. выпуклый многоугольник, обхватывающий все точки) есть четырёхугольник. Если выпуклая оболочка является пятиугольником, то любые четыре точки можно соединить так, что они образуют четырёхугольник. Треугольная выпуклая оболочка постоянно содержит снутри две точки; тут — D и E. Линия DE разделяет треугольник на две части так, что две точки, A и B, лежат по одну сторону от неё. Четыре точки ABCD должны создавать выпуклый четырёхугольник.
Эрдёш и Клейн стремительно отыскали обобщение начальной задачки. Они сообразили, что 5 из 9 точек на плоскости постоянно образуют выпуклый пятиугольник. Тогда они предложили новейшую задачку: если число точек на плоскости равно 1+2k–2
, где k=3, 4, 5 … и т.д., то можно ли постоянно избрать k точек, образующих выпуклый многоугольник?
В собственных мемуарах Шекереш так обрисовывает следующие действия: «Мы скоро поняли, что обыкновенные рассуждения не подступают, и возникло волнующее чувство, что в нашем кружке в первый раз появился новейший тип геометрических задач». Шекереш показал, что существует такое число n, что если n точек лежат на плоскости так, что никакие три из их не находятся на одной прямой, то посреди их постоянно можно отыскать k точек, образующих выпуклый k-угольник. Иными словами, если точек довольно много, постоянно можно отыскать их подмножество, образующее многоугольник с данным числом сторон. Доказав это, Шекереш поновой открыл аксиому Рамсея, хотя никто из их группы в то время не знал о ней.
В 1934году Эрдёш и Шекереш выпустили свои результаты, хотя ни они, ни кто-нибудь иной до сего времени не смогли обосновать догадку Эрдёша о том, что числа точек n=1+2k–2
довольно. Эрдёш нередко именует эту совместную публикацию «статьёй со счастливым концом», так как скоро опосля её опубликования Шекереш и Клейн поженились. Эрдёш же стал самым продуктивным математиком нашего столетия.
Эрдёш заинтересовался мыслью Рамсея о том, что всякая довольно большая структура обязана содержать регулярную подструктуру данного размера. Но ему хотелось выяснить, какого конкретно размера обязана быть эта структура, чтоб существование определённой подструктуры было гарантировано. Так Эрдёш начал работать над вариантом головоломки о вечеринке.
В этом варианте 6 человек представлены шестью точками. Для удобства точки размещаются на плоскости так, чтоб никакие три из их не лежали на одной прямой. Точки соединяются ребром, которое окрашивается, чтоб представить дела меж надлежащими 2-мя людьми. Красноватое ребро значит, что эти люди меж собой знакомы, а голубое ребро — что они друг друга не знают.
Как следует, если три человека знакомы вместе, то рёбра меж надлежащими точками образуют красноватый треугольник, а если эти трое незнакомы, то появляется голубий треугольник. Головоломку о вечеринке тогда можно сконструировать так: правильно ли, что если каждое ребро, соединяющее любые две из 6 точек, окрасить в голубий либо красноватый цвет произвольным образом, то постоянно возникает или голубий, или красноватый треугольник?
задачка, которую изучал Эрдёш, представляет собой обобщение данной задачки. Он обусловил полную сеть как набор точек, любая из которых соединена рёбрами со всеми остальными. Потом он задался вопросцем: какова меньшая полная сеть, которая будучи произвольным образом раскрашена в красноватый и голубий цвет, непременно содержит полную сеть красноватого либо голубого цвета? Ответ последующий: полная сеть — из 6 точек. Эту задачку и её решение удобнее выразить так: число Рамсея (R) для трёх бардовых и трёх голубых равно 6.
Как насчет числа Рамсея для 5 бардовых и трёх голубых? Иными словами, какова меньшая полная сеть, которая будучи произвольным образом раскрашена в красноватый и голубий цвет, непременно содержала бы или красноватую сеть из 5 точек, или голубую сеть из трёх точек? Число Рамсея для 5 бардовых и трёх голубых равно 14, что обосновали лишь в 1955году Роберт Гринвуд из Института шт.Техас в Остине и Эндрю Глисон из Гарвардского института.



5 < R(3,3) = 6
8 < R(3,4) = 9
13 < R(3,5) = 14


17 < R(3,6) = 18
22 < R(3,7) = 23


27 < R(3,8) ≤ 29
35 < R(3,9) = 36
Рис.2. Числа Рамсея определяются как меньшее сеть бардовых рёбер, или некая группа из k точек образует полную сеть голубых рёбер. Картинки демонстрируют, как велико обязано быть конкретное число Рамсея. На первой диаграмме изображены 5 точек, соединённые красноватыми и голубыми рёбрами таковым методом, что никакие три точки не образуют ни красноватой, ни голубой полной сети. Как следует, из первой диаграммы можно вывести, что число Рамсея для трёх бардовых и трёх голубых больше 5. Аналогично можно утверждать, что из 2-ой диаграммы следует, что число Рамсея для трёх бардовых и четырёх голубых больше восьми. Иными наиболее сложными способами можно показать, что число Рамсея для трёх бардовых и трёх голубых равно 6, а число Рамсея для трёх бардовых и четырёх голубых равно 9. Все буквально известные числа Рамсея приведены выше, не считая числа Рамсея для четырёх бардовых и четырёх голубых, диаграмма для которого изображена на рис.1. (На неких диаграммах голубые рёбра для простоты не показаны.) Относительно числа Рамсея для трёх бардовых и восьми голубых было подтверждено, что оно больше 27 и меньше либо равно 29. Не так давно было показано (но пока не доказано), что оно равно 28.
Числа Рамсея очень тяжело вычислять. Усилиями поколений математиков и компов удалось отыскать только семь чисел Рамсея, которые приведены на рис.2. Чтоб наглядно показать трудность вычисления чисел Рамсея, Эрдёш нередко ведает последующий смешной рассказ. Инопланетяне вторглись на землю и грозят убить её через год, если население земли не сумеет отыскать число Рамсея для 5 бардовых и 5 голубых. Мы могли бы мобилизовать наилучшие мозги и самые быстродействующие компы, тогда и в течение года мы, может быть, смогли бы отыскать разыскиваемое
Эрдёш всё же нашёл метод получить некое большенный полной сети, не содержащую ни красноватой, ни голубой сети из трёх точек? Таковая раскраска полной сети из 5 точек показана на рис.2. Отсюда следует, что число Рамсея для трёх бардовых и трёх голубых обязано быть больше 5. 5 есть нижняя граница для этого числа Рамсея.
В 1947году Эрдёш предложил необыкновенный способ отыскания нижней границы хоть какого числа Рамсея: бросание монеты. Он предпринял мысленный согласовании с результатом бросания «истинной» монеты (т.е. монеты, для которой возможность выпадения сокола либо решки строго схожа и равна 1/2. — Перев.). Ребро окрашивается в красноватый цвет, если выпадает решка, и в голубий, если выпадает орёл. Потом он попробовал обосновать, что число Рамсея, скажем, для 34 бардовых и 34 голубых больше миллиона. Опыт считается удачным, если в итоге таковой случайной раскраски не появляется ни красноватой, ни голубой сети из 34 точек.
Вроде бы он мог гарантировать фуррор? Любые 34 точки соединяются 561 ребром. Если 1-ое бросание предписывает голубий цвет для первого ребра, то для получения голубой сети нужно, чтоб последующие 560 бросаний тоже предписывали голубий цвет. Возможность того, что это произойдёт, равна 2–561
. Возможность возникновения красноватой сети буквально таковая же, так что общая возможность появления одноцветной сети в два раза больше, либо приблизительно 2,6×10–169
.
сейчас вспомним, что число наборов из 34 точек, избранных из миллиона точек, равно
1000000!
34! · 999966!
≈3,4×10165
.
Тем можно ждать, что из всех вероятных полных сетей из 34 точек одноцветными будут 3,4×10165
×2,6×10–169
, либо примерно 0,001. Итак, в 99,9% случаев мысленный подтверждение от неприятного. Он представил, что никакая схема раскраски не является удачной. Тогда мысленный означает, это предположение обязано быть неверным, т.е. обязана существовать удачная схема раскраски (не с вероятностью 99,9%, а с абсолютной достоверностью). Существование таковой раскраски значит, что один миллион является нижней границей для 34 бардовых и 34 голубых.
Такое рассуждение, известное как вероятностный способ, даёт лучшие нижние оценки для чисел Рамсея. Но этот способ не содержит никаких указаний на то, как в реальности следует создавать желаемую раскраску. В попытках получить такие раскраски исследователи употребляют обеспеченный арсенал приёмов из теории чисел, теории множеств и остальных разделов арифметики. Хотя приобретенные при всем этом результаты увлекательны, они пока не добиваются оценок, которые даёт способ бросания монеты.
Значимая часть ранешних исследовательских работ по теории Рамсея была посвящена огромным количествам точек и линий, но всё же в почти всех из их рассматривались и огромного количества чисел. Голландский математик Бартель Л.Ван дер Варден начал решать такие задачки ещё до того, как Рамсей обосновал свою аксиому.
В 1926 году Ван дер Варден повстречался с увлекательной задачей, связанной с арифметическими прогрессиями. Как надо из самого наименования, арифметическая прогрессия — это таковая последовательность чисел, в какой разность меж 2-мя примыкающими членами остаётся неизменной. к примеру, последовательность 3, 5, 7 есть трёхчленная арифметическая прогрессия, в какой разность меж примыкающими членами равна двум. Личный вариант задачки, привлёкшей внимание Ван дер Вардена, можно сконструировать так. Если каждое целое число от 1 до 9 напечатать на страничке одной из 2-ух красок, красноватой либо голубой, то постоянно ли найдутся три голубых либо три бардовых числа, образующие арифметическую прогрессию? Ответ даётся в последующей врезке.
Теория Рамсея и арифметические прогрессии
Арифметическая прогрессия — это последовательность чисел, в какой разность меж примыкающими членами остаётся неизменной. к примеру, 7, 10, 13, 16 — это арифметическая прогрессия, в какой разность меж примыкающими членами равна трём. Из теории Рамсея следует такое утверждение о арифметических прогрессиях: если каждое число от 1 до 9 выкрасить в красноватый либо голубий цвет, то или три голубых числа, или три бардовых образуют арифметическую прогрессию.
Чтоб обосновать это утверждение, мы могли бы проверить все 512 методов раскраски 9 чисел. Но мы можем обосновать его, рассмотрев лишь два варианта. Начнём со варианта, в каком 4 и 6 имеют однообразный цвет, скажем голубий.
1 2 3 4 5 6 7 8 9
Чтоб избежать голубой арифметической прогрессии 4, 5, 6, мы покрасим 5 в красноватый цвет.
1 2 3 4 5 6 7 8 9
Чтоб избежать голубых арифметических прогрессий 2, 4, 6 и 4, 6, 8, мы покрасим 2 и 8 в красноватый цвет.
1 2 3 4 5 6 7 8 9
Но тогда у нас получится красноватая арифметическая прогрессия 2, 5, 8. Итак, если 4 и 6 имеют однообразный цвет, то постоянно получится или красноватая, или голубая арифметическая прогрессия. сейчас разглядим вариант, когда 4 и 6 имеют разный цвет. Число 5 можно выкрасить как угодно, не создав при всем этом арифметической прогрессии, так что мы произвольно покрасим 5 в красноватый цвет.
1 2 3 4 5 6 7 8 9
Продолжим раскрашивание последующим образом:
3, чтоб избежать 3 4 5
9, чтоб избежать 3 6 9
7, чтоб избежать 5 7 9
8, чтоб избежать 6 7 8
2, чтоб избежать 2 5 8
1, чтоб избежать 1 2 3
Такое раскрашивание даёт последовательность
1 2 3 4 5 6 7 8 9
Но в ней всё равно осталась красноватая арифметическая прогрессия 1, 5, 9. Таковым образом, независимо от того, в однообразный либо в различные цвета покрашены 4 и 6, постоянно имеется или голубая, или красноватая арифметическая прогрессия.
Ван дер Варден поставил впереди себя последующую задачку, являющуюся обобщением предшествующей: обосновать, что если n — довольно огромное число и все целые числа от 1 до n написаны на страничке одним из 2-ух произвольно избираемых для каждой числа цветов, то постоянно существует одноцветная последовательность с определённым числом членов, являющаяся арифметической прогрессией. Это утверждение можно считать аксиомой Рамсея для арифметических последовательностей, хотя оно общеизвестно под заглавием аксиомы Ван дер Вардена.
Ван дер Варден призвал на помощь собственных коллег Эмиля Артина и Отто Шрейера. Позже он писал: «Мы пришли в кабинет Артина на факультет арифметики Гамбургского института и попробовали отыскать подтверждение. Мы отрисовывали на доске какие-то картинки. У нас было состояние, которое немцы именуют Einfälle (озарение), когда в голову приходят нежданные идеи. Пару раз такие новейшие идеи направляли обсуждение в новое русло, и одна из их в конце концов привела к решению». Оказалось, но, что Ван дер Варден не сумел обосновать этот итог для 2-ух красок, не доказав его для варианта, когда сразу употребляется случайное число красок.
В своём подтверждении Ван дер Варден применил особенный вид математической индукции. Рядовая (одинарная) индукция содержит в себе два шага. На первом шаге необходимо показать, что утверждение производится для некого малого числа, скажем, для 2-ух. На втором шаге доказывается, что если утверждение справедливо для какого-нибудь числа, то оно справедливо и для числа, на единицу большего. Отсюда следует, что оно правильно для трёх, четырёх и так дальше. Результаты «идут в руки» один за остальным как нескончаемая очередь падающих костяшек домино, поставленных на ребро: если столкнуть одну, то свалятся все.
Чтоб обосновать аксиому Рамсея для арифметических прогрессий, Ван дер Варден применил наиболее узкую, двойную индукцию. Он представил, что для хоть какого фиксированного числа красок существует число n, такое, что если каждое целое число в интервале от 1-го до n напечатать какой-либо из этих красок, то найдётся арифметическая прогрессия чисел 1-го цвета, состоящая, скажем, из 10 членов. Делая упор на это допущение, он сумел показать, что для хоть какого фиксированного набора красок существует число m, такое, что если каждое целое число в интервале от 1 до m напечатать какой-либо из этих красок, то будет существовать одноцветная арифметическая прогрессия из 11 членов. В общем, он показал, что из результатов для k членов и хоть какого количества красок вытекает итог для k+1 членов и хоть какого количества красок.
Опосля того как Ван дер Варден добрался до данной стадии подтверждения, ему осталось лишь показать, что его предположение вправду правильно для некого малого значения k. Если целых чисел на единицу больше, чем красок, то постоянно найдутся два числа 1-го цвета. Эти два числа образуют арифметическую прогрессию из 2-ух членов. Потому одноцветная арифметическая прогрессия постоянно существует, если чисел на единицу больше, чем красок. Нескончаемая последовательность фишек домино для 2-ух членов сейчас сталкивает нескончаемую последовательность домино для трёх членов, которая, в свою очередь, сталкивает нескончаемую последовательность домино для четырёх членов, и так дальше (см. последующую врезку).
Теория Рамсея и игра «крестики-нолики»
В 1926году Бартель Л. Ван дер Варден обосновал, что если n — довольно огромное число и если все числа от 1 до n произвольным образом раскрасить каким-либо из 2-ух цветов, то постоянно найдётся одноцветная арифметическая прогрессия с определённым числом членов. В 1963году А.Хейлз и Р.Джуитт открыли то, что оказалось сущностью аксиомы Ван дер Вардена, изучая игру «крестики-нолики». Хотя традиционный вариант данной игры с игровым полем размером три на три может стремительно наскучить, трёхмерный вариант с 4-мя полями в любом ряду очень увлекателен. «Доской» для трёхмерной игры служит куб, разбитый на 64 ячейки. Игроки по очереди заполняют ячейки крестиками либо ноликами, пока один из их не выигрывает, заполнив четыре ячейки, расположенные на одной прямой. И двумерная, и трёхмерная игра иногда кончается ничьей. Как обстоит дело в случае игр наиболее высочайшей размерности? Можно ли гарантировать выигрыш в неком n-мерном варианте крестиков и ноликов с k элементами на одной прямой?
Хейлз и Джуитт проявили, что если размерность n довольно велика, то постоянно можно отыскать вариант игры с k элементами на одной прямой, который никогда не кончается ничьёй. к примеру, независимо от того, как размещены крестики и нолики в трёхмерной игре с 3-мя элементами в ряду, постоянно или три крестика будут размещены на одной прямой, или три нолика.
Аксиому Ван дер Вардена можно вывести из результата Хейлза и Джуитта, применив преобразование, переводящее прямые данной игры в арифметические прогрессии. Разглядим трёхмерную игру с 3-мя элементами в ряду.
Координаты крестиков в данной выигрышной композиции сущность 121, 222 и 323; рассматриваемые как числа, они образуют арифметическую прогрессию. Можно показать, что всякая выигрышная композиция, перевоплощенная сиим способом, даёт арифметическую прогрессию.
1
1
2 ×
3
1 2 3
2
1
2 ×
3
1 2 3
3
1
2 ×
3
1 2 3
Доказав аксиому Рамсея для арифметических прогрессий, Ван дер Варден применил эти познания к решению последующей задачки. Каково меньшее больше млрд, больше чем 10 в степени млрд.
По правде, чтоб выразить его итог, арифметики прибегают к последовательности функций, известной как иерархия Аккермана. 1-ая функция в данной иерархии именуется просто DOUBLE(x). Как дает подсказку заглавие (double — означает, удвоить), эта функция умножает к примеру, чтоб отыскать EXPONENT(3), мы удваиваем 1, потом удваиваем итог предшествующего деяния и потом опять удваиваем итог. По сути неважно какая функция в иерархии Аккермана определяется через предшествующую.
Итак, третью функцию данной иерархии, TOWER(x), можно выразить при помощи функции EXPONENT. TOWER(3), к примеру, — это 2 в степени 2 в степени 2, что равно 2 в степени 4, т.е. 16. TOWER(x) время от времени записывают в виде «башни» (tower — означает, башня) характеристик степеней,
2
…2
2
2
где x — число двоек в данной башне. Но даже функция TOWER(x) растёт недостаточно стремительно, чтоб можно было записать итог Ван дер Вардена.
Последующую функцию, известную под шуточным прозвищем WOW(x) (английское междометие WOW приблизительно соответствует русским «Ой!», «Ах!» и «Ну и ну!». — Перев.), можно отыскать, если начать с 1 и применить x раз функцию TOWER. Тогда,
WOW(1) = TOWER(1) = 2,
WOW(2) = TOWER(2) = 4,
WOW(3) = TOWER(4) = 65536.
Чтоб отыскать WOW(4), необходимо вычислить TOWER(65536). Чтоб это создать, необходимо начать с 1 и применить функцию EXPONENT 65536 раз. Даже применение функции EXPONENT всего только 5 раз даёт 265536
, — число, которое, будучи записанным цифра за цифрой, заполнило бы две странички этого журнальчика. По сути даже число, заполняющее все странички всех книжек и всю память всех компов, всё же остается несравненным с WOW(4).
Тем не наименее, чтоб всё-таки записать итог Ван дер Вардена, придётся найти функцию, которая растёт ещё резвее. Функция ACKERMANN(x) определяется последовательностью DOUBLE(1), EXPONENT(2), TOWER(3), WOW(4) итакдалее. ACKERMANN(x) в конце концов растёт резвее хоть какой функции в данной иерархии. подтверждение Ван дер Вардена даёт последующий количественный итог: если числа 1, 2, …, ACKERMANN(k) раскрашены 2-мя красками, то постоянно существует одноцветная арифметическая прогрессия длиной k.
Кажется странноватым, что такие страшные числа могут появиться из настолько невинного утверждения, касающегося лишь арифметических прогрессий. Почти все арифметики в течение почти всех лет пробовали сделать лучше подтверждение Ван дер Вардена. Беда следовала за неудачей, и в итоге сделалось укрепляться убеждение в том, что двойная индукция и соответственно функция ACKERMANN являются необходимыми компонентами хоть какого подтверждения аксиомы Ван дер Вардена. Всё почаще логики пробовали отыскать доказательства тому, что так оно и есть по сути.
В 1987году, но, израильский логик Саарон Шела из Еврейского института в Иерусалиме достигнул большого фуррора. Шела обширно признан как человек, лучше всех справляющийся с решением сложнейших задач в современной арифметике. Он смог преодолеть барьер функции ACKERMANN и показал последующее: если целые числа от 1 до WOW(k) раскрасить в два цвета, то постоянно найдётся одноцветная арифметическая прогрессия длиной k членов.
Невзирая на свою специализацию, Шела совсем не употребляет в своём подтверждении каких-то средств математической логики. В нём использованы только простые (но очень смышленые) математические идеи. На сто процентов выписанное, его подтверждение занимает примерно четыре странички, и большая часть профессионалов находит его наиболее чётким, чем первоначальное подтверждение Ван дер Вардена. Что самое принципиальное, он обошёлся без двойной индукции. Он фиксирует число красок на 2-ух (либо любом другом определенном значении) и потом проводит обыденную индукцию: если утверждение правильно для прогрессий длиной k членов, то оно также справедливо и для прогрессий длиной k+1.
Арифметики на данный момент пробуют осознать, можно ли сделать лучше подтверждение Шелы, чтоб получить для аксиомы Ван дер Вардена оценку порядка TOWER либо даже EXPONENT. один из нас (Грэм) предложил премию в размере 1000 баксов тому, кто обоснует (либо опровергнет) утверждение, что для всякого k раскрашенная в два цвета совокупа чисел от 1 до TOWER(k) содержит одноцветную арифметическую прогрессию из k членов.
Усилиями Рамсея, Эрдёша, Ван дер Вардена и почти всех остальных были заложены базы теории, носящей имя Рамсея. Пока что исследователи лишь начали учить следствия данной теории. Она дозволяет представить, что структурная база арифметики состоит из очень огромных чисел и множеств — объектов настолько большенных, что их тяжело даже выразить, а тем наиболее понять.
Когда мы научимся обращаться с этими большенными числами, мы сможем отыскать математические соотношения, которые посодействуют инженерам создавать огромные сети коммуникаций, а учёным распознавать упорядоченные структуры в крупномасштабных физических системах. сейчас мы с лёгкостью прослеживаем в созвездиях на ночном небосклоне следствие теории Рамсея. А какие структуры можно отыскать в огромных количествах, размеры которых в ACKERMANN(9) раз больше?

Рис.4. Понятия теории Рамсея приложимы к геометрическим задачкам вроде данной головоломки о шестиугольниках. Если длины всех сторон шестиугольников равны 0,45 единицы (единица длины быть может случайной), то две точки снутри шестиугольника отстоят друг от друга самое большее на 0,9 единицы. Любой шестиугольник окрашивается одним из 7 цветов, так, что никакие два шестиугольника 1-го цвета не отстоят друг от друга меньше чем на 1,19 единицы. Никакие две точки 1-го цвета не находятся одна от иной на расстоянии, в точности равном единице. Пока что никто не сумел найти, можно ли раскрасить плоскость шестью красками так, чтоб никакие две точки 1-го цвета не находились в точности на расстоянии одной единицы друг от друга.
Перечень
литературы
1. A.M.Gleason and R.E.Greenwood. Combinatorial Relations and Cromatic Graphs. In: Canadian Journal of Mathematics, 1955, v.7, No.1, pp.1–7.
2. B.L. van der Waerden. How the Proof of Baudet’s Conjecture Was Found. In: Studies in Pure Mathematics (Edited by L.Mirsky). Academic Press, Inc., 1971.
3. Paul Erdös: The Art of Counting: Selected Writings (Edited by Joel Spencer). The MIT Press, 1973.
4. Paul Hoffman. The Man Who Loves Only Numbers. In: Atlantic Monthly, 1987, v.260, No.5, pp.60–74.
5. R.L.Graham and V.Rödl. Numbers in Ramsey Theory, in Surveys and in Combinatorics. London Mathematical Society Lecture Notes Series, 1987, No.123, pp.111–153.
6. Ronald L.Graham, Bruce L.Rothschild and Joel H.Spencer. Ramsey Theory. Second Edition. John Wiley & Sons, Inc., 1990.
]]>

 (5 оценок, среднее: 4,80 из 5)
(5 оценок, среднее: 4,80 из 5)