Загрузка...
Учебная работа. Реферат: Характеристики систем автоматического управления
Тема:
«свойства систем автоматического управления»
1. Статические свойства САУ
Статические свойства определяют статику системы, т.е. ее поведение в установившемся режиме.
именуется отношение выходной величины к входной величине в установившемся режиме.
Статические свойства разрешают: найти коэффициент усиления системы; степень ее нелинейности; величину статизма; произвести согласование рабочих точек системы.
2. Динамические свойства САУ
Динамические свойства определяют динамику системы, т.е. ее поведение в неустановившемся (переходном) режиме. При всем этом употребляют последующие главные динамические свойства:
–
–
2.1 Передаточная функция системы и ее характеристики
Дифференциальное уравнение линейной системы имеет вид:
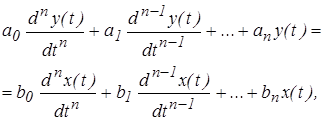(1)
где аi
и bi
– характеристики системы,
—порядок системы.
Если применим аксиомы Лапласа при нулевых исходных критериях, то дифференциальное уравнение в операторной форме запишется последующим образом
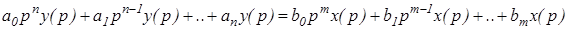
где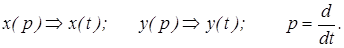 
На физическом уровне нулевые исходные условия обозначают, что до приложения действия система находилась в покое.
есть отношение изображения выходной величины к изображению входной величины при нулевых исходных критериях
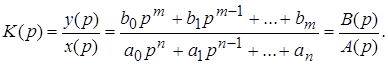(2)
Главные характеристики передаточной функции:
1. Передаточная функция является полной чертой системы.
Она на сто процентов охарактеризовывает статические и динамические характеристики системы.
2. Статический коэффициент усиления, т.е. коэффициент усиления в установившемся режиме (при
либо
равен
.
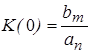3. Полином знаменателя именуется характеристическим, а
именуется характеристическим уравнением. Корешки полинома знаменателя именуются полюсами, а числителя нулями.
Степень полинома числителя не превосходит степени полинома знаменателя (
), в неприятном случае система является на физическом уровне нереализуемой.
5. Коэффициенты полиномов ai
и bi
обоснованы настоящими физическими параметрами системы.
6. Передаточная функция быть может задана в виде нулей и полюсов в графическом виде.
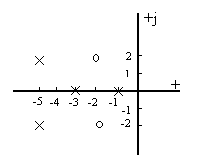
Рис. 1
к примеру, для приведенного на рис. 1 расположения нулей (0) и полюсов (х) передаточная функция имеет вид:
.
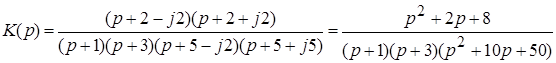2.2 Временные свойства САУ
именуется законконфигурации выходной величины в функции времени при изменении входного действия по определенному закону и при условии, что до приложения действия система находилась в покое. Временные свойства определяются как реакция системы на типовые действия при нулевых исходных критериях.
К главным временным чертам относятся переходная функция и функция веса.
Типовые действия
. В качестве типовых действий при исследовании систем употребляются:
–
(употребляется при исследовании стохастических систем).
Единичная функция.
– действие, амплитуда которого равна 0 при
< 0 и равна 1 при
³ 0.
характеристики единичной функции и единичной функции со сдвигом определяются соотношениями:
либо 
(3)
а их графическое изображение имеет вид, приведенный на рис. 2а, б.
а) б)
Рис. 2
При всем этом изображение единичного действия имеет вид:
(4)
Единичный импульс.
(
– функция) – это идеализированный сигнал, который характеризуется нескончаемо малой продолжительностью, нескончаемо огромным уровнем (амплитудой) и площадью равной единице.
Единичный импульс и импульс со сдвигом описываются соотношениями:
либо 
(5)
а их графическое изображение имеет вид, приведенный на рис. 3а, б.
а) б)
Рис. 3
При всем этом изображение единичного импульса имеет вид
(6)
Главные характеристики дельта – функции
1.
– площадь либо интенсивность
– функции;
2. 
-фильтрующее свойство;
3. 
;
— связь
– функции с единичной функцией;
5. 
.
характеристики дельта – функции обширно употребляются в способах исследования САУ.
Линейно-растущее действие.
это действие с неизменной скоростью конфигурации сигнала. Такое действие почаще всего употребляется для определения точности систем и описывается соотношением:
. (7)
Графическое изображение линейно – возрастающего действия имеет вид, приведенный на рис. 4а.
При всем этом,
. (
8)
а) б)
Рис. 4
Квадратичное действие.
– это воздей-ствие с неизменным убыстрением конфигурации сигнала. Такое действие почаще всего употребляется для определения точности систем и описывается соотношением:
. (9)
Графическое изображение квадратичного действия имеет вид, приведенный на рис. 5.
При всем этом,
. (10)
Переходная функция.
– реакция системы на единичное действие при нулевых исходных критериях.
Пусть задана система (рис. 5) с передаточной функцией
Рис. 5
В изображениях выходная величина равна 
.
Потому что
то изображение выходной величины равно
.
При всем этом связь меж передаточной и переходной функцией имеет вид:
. (11)
Изначальное
. (12)
Весовая функция.
– реакция системы на единичный импульс при нулевых исходных критериях.
Пусть задана система (рис. 6) с передаточной функцией
Рис. 6
В изображениях выходная величина равна , а в оригиналах определяется при помощи интеграла свертки
. (13)
Потому что 
, то 
.
При всем этом связь меж передаточной и весовой функцией имеет вид:
, (14)
т.е. весовая функция представляет оригинал передаточной функции.
Установившееся
. (15)
Связь меж переходной и весовой функцией имеет вид:
. (16)
способы определения временных черт
Есть разные способы расчета переходных действий, при всем этом более нередко употребляются последующие способы:
1. Традиционный способ.
2. Операторный способ, использующий разложение на обыкновенные дроби.
3. Операторный способ, использующий вычеты.
Способ аналогового и цифрового моделирования.
5. способ трапеций.
Разглядим некие способы определения временных черт на определенных примерах.
Традиционный способ расчета временных черт
Традиционный способ расчета временных черт основан на решении дифференциальных уравнений.
Пример 1.
Пусть дана передаточная функция: 
Найти: переходную функцию –
и функцию веса –
.
Решение
1. Запишем дифференциальное уравнение в согласовании с данной передаточной функцией
При единичном действии, т.е.
дифференциальное уравнение имеет вид
.
2. Общее решение неоднородного дифференциального уравнения состоит из вольной и принужденной составляющей
.
3. Переходная функция быть может определена из соотношения
При нулевых исходных критериях
При всем этом выражения для переходной функции и функции веса имеют вид:
способ разложение на обыкновенные дроби
Разглядим метод использования способа на прошлом примере. Определим функцию веса для данной системы.
Начальную передаточную функцию можно представить в виде:
значения характеристик А и В находим способом неопределенных коэффициентов
Функция веса равна: 
Определим переходную функцию.
Изображение переходной функции можно представить в виде:
значения характеристик А, В и С находим способом неопределенных коэффициентов.
Переходная функция равна: 
Определение временных черт с внедрением вычетов
Разглядим метод использования способа на прошлом примере. Определим функцию веса для данной выше системы. В согласовании с аксиомой разложения:
если
где 
,
то
.
Таковым образом, используя аксиому Коши о вычетах, оригинал можно найти как сумму вычетов по полюсам подынтегральной функции.
Разглядим изображение переходной функции:
Запишем характеристическое уравнение, определим значения полюсов их количество и кратность
При всем этом переходную функцию определяем, используя вычеты по полюсам подынтегральной функции
Функция веса определяем аналогично, или через производную от переходной функции
2.3 Частотные свойства САУ
определяются, как реакция системы на гармоническое типовое действие при нулевых исходных критериях.
Пусть задана система (рис. 7) с передаточной функцией
.
Рис. 7
При подаче на вход системы гармонического действия
, (17)
на выходе получим 
(18)
Если употреблять формулы Эйлера, эти соотношения можно представить в всеохватывающем виде:
(19)
Если выполнить подстановку
в передаточной функции системы, то получим всеохватывающую передаточную функцию
(20)
При изменении частоты 0£
£+¥ получим последующие частотные свойства:
АФХ – амплитудно-фазовая частотная черта;
ВЧХ – вещественная частотная черта;
МЧХ – надуманная частотная черта;
АЧХ – амплитудно-частотная черта;
ФЧХ – фазовая частотная черта.
Частотные свойства могут быть выражены через коэффициенты полиномов передаточной функции
(21)
Графически свойства можно представить в виде рис. 8а.
Связь меж временными и частотными чертами.
Разглядим связь меж частотными чертами и переходной функцией системы (рис. 8б).
а) б)
Рис. 8
Для выходной величины можно записать
.
Используя преобразование Фурье, получим выражение для переходной функции
(22)
Подставив эти выражения в формулу для
и выполнив преобразования, получим связь меж переходной функцией и ВЧХ:
(23)
Логарифмические частотные свойства САУ
исследование систем значительно упрощается при использовании не обыденных, а логарифмических частотных черт. При всем этом натуральная логарифмическая амплитудная и фазовая частотные свойства определяются из соотношений
. (24)
На практике обычно употребляют десятичные логарифмы. При всем этом логарифмическая амплитудно-частотная черта (ЛАЧХ) строится в логарифмическом масштабе частот и определяется соотношением
.
Единицей измерения ЛАЧХ является
(дБ ), 1дБ = 1/10 [Бел].
Потому что 1 Бел соответствует повышению мощности в 10 раз, то
(25)
Амплитуда сигнала откладывается по оси ординат (рис. 9а), при всем этом ось абсцисс соответствует значению амплитуды равной единице, верхняя полуплоскость соответствует усилению сигнала (A > 1), а нижняя – ослаблению (A < 1).
Логарифмическая фазовая частотная черта (ЛФЧХ) строится в логарифмическом масштабе частот, при всем этом частоты откладываются по оси абсцисс по декадам (рис. 9б). Декада – отрезок, на котором частота возрастает в 10 раз.
а) б)
Рис. 9
Начало оси координат, зависимо от спектра частот, на котором строится логарифмическая черта, быть может помещено в всякую точку (
= 0,01;
= 0,1;
= 1 и т.д.).
Логарифмические свойства имеют ряд преимуществ перед обыкновенными частотными чертами. Главным преимуществом логарифмических черт является возможность оценки воздействия отдельных характеристик системы без необходимости повторного проведения расчета.
Литература
1. Автоматическое проектирование систем автоматического управления. / Под ред. В.В. Солодовникова. – М.: Машиностроение, 1990. -332 с.
2. Бойко Н.П., Стеклов В.К. системы автоматического управления на базе микро-ЭВМ . – К.: Тэхника, 1989. –182 с.
3. В.А. Бесекерский, Е.П. Попов «Теория систем автоматического управления». Профессия, 2003 г. – 752 с.
4. Воронов А.А., Базы теории автоматического управления, ч. 3, М. – Л., 1970.
5. Гринченко А.Г. Теория автоматического управления: Учебн. пособие. – Харьков: ХГПУ, 2000. –272 с.
6. Емельянов С.В., системы автоматического управления с переменной структурой, М., 1967.
7. Макаров И.М., Менский Б.М. Линейные автоматические системы. — М.: Машиностроение, 1982.
8. Справочник по теории автоматического управления. / Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.
]]>