Загрузка...
Учебная работа. Курсовая работа: Построение изображений ландшафта в реальном времени
Кафедра «Программное обеспечение ЭВМ и информационные технологии»
Курсовой проект
по машинной графике
Расчётно-пояснительная записка
Тема:
«Построение изображений ландшафта в настоящем времени»
Оглавление
1. Введение
2. Конструкторская часть
2.1 Выбор, обоснование и описание применяемых алгоритмов и понятий машинной графики
2.1.1 Равномерная сетка высот
2.1.2 Выравнивание ландшафта
2.1.3 Трехмерные аффинные преобразования
2.1.4 Проецирование
2.1.5 Отображение в окне
2.1.6 метод Z-буфера
2.1.7 Освещение
2.1.7.1 Однотонная закраска (способ гранения)
2.1.7.2 Способ Гуро
2.1.7.3 Способ Фонга
2.1.7.4 анализ способов Гуро и Фонга
2.1.8 Последовательность действий при визуализации сцены
2.2 Типы, структуры данных и функции, использованные при реализации программного комплекса
2.2.1 структура файла для хранения карт изообластей
2.2.2.4 Распределение программки по модулям
2.2.2.5 Связи меж модулями программки
2.2.3 программка «Просмотр ландшафта»
2.2.3.1 Процедуры манипуляции изображением ландшафта
2.2.3.2 Z-буфер
2.2.3.3 Буфер кадра
2.2.3.4 Процедуры визуализации ландшафта
2.2.3.2 Тип и структура файла для хранения ландшафта
2.2.3.3 Распределение программки по модулям
2.2.3.4 Связи меж модулями программки
3. Технологическая часть
3.1 Выбор языка программирования
3.2 Описание программного комплекса
3.2.1 программка «Редактор карт»
3.2.1.1 Общие сведения
3.2.1.2 интерфейс программки
3.2.1.3 Работа программки
3.2.2 программка «Просмотр ландшафта»
3.2.2.1 Общие сведения
3.2.2.2 интерфейс программки
3.2.2.3 Работа программки
3.2.3 Системные требования
4. Экспериментально-исследовательская часть
4.1 Исследование № 1
4.2 Исследование № 2
4.3 Исследование № 3
5. Заключение
6. Перечень литературы
1. Введение
Решение задачки построения поверхности на базе карты изолиний либо изообластей высот является одним из шагов сотворения геоинформационной системы (it система, которая хранит в базе данных описание и обеспечивает анализ объектов, расположенных на поверхности Земли). Описание поверхности изолиниями высоты нередко употребляется, к примеру, в картографии. В данной работе решается задачка построения изображения ландшафта на базе карты изообластей высот в настоящем времени.
В свою очередь задачка построения изображения ландшафта на базе карты изообластей содержит в себе последующие задачки:
· преобразование данной карты в равномерную сетку высот;
· триангуляция приобретенной сетки высот;
· по мере необходимости – выравнивание триангулированной сетки для получения изображений ландшафтов, близких по очертаниям к настоящим.
Требование к скорости построения изображений ландшафта (для удобной работы нужна производительность порядка 30 кадров в секунду [1]) описывает выбор метода машинной графики, применяемого для визуализации сцены – метод Z-буфера в большей степени отвечает этому требованию, потому что он является более обычным в собственной группе и просит меньшего количества вычислительных ресурсов.
Не считая этого, в данной работе затронуты остальные методы машинной графики: преобразование координат, проецирование, освещение.
При работе с освещением реализованы последующие методы наполнения плоских граней (в данной работе — треугольников):
· способ гранения (монотонной закраски с учетом ориентации нормали к плоскости грани);
· способ Гуро – способ закрашивания граней трехмерных объектов, который употребляет билинейную интерполяцию интенсивности цвета в верхушках граней;
· способ Фонга – способ, основанный на билинейной интерполяции векторов нормалей в верхушках граней.
Цель данной работы – воплотить перечисленные методы в разрабатываемом программном комплексе.
В программке также предусмотрен удачный русский пользовательский интерфейс, позволяющий редактировать карты изообластей высот, также управлять получаемым изображением ландшафта (вращать его относительно координатных осей, масштабировать, изменять цвет поверхности и т.д.).
2. Конструкторская часть
2.1 Выбор, обоснование и описание применяемых
алгоритмов и понятий машинной графики
2.1.1 Равномерная сетка высот
Существует огромное количество моделей описания поверхностей. Более всераспространенными из их являются:
· аналитическая модель – для описания поверхности употребляются математические формулы, к примеру функции от 2-ух аргументов z = f(x, y);
· векторная полигональная модель – для описания пространственных объектов употребляются такие элементы, как верхушки, векторы, полилинии, полигоны, полигональные поверхности;
· воксельная модель – представляет собой трехмерный растр. Подобно тому, как пиксели размещаются на плоском изображении, воксели образуют трехмерные объекты в неком объеме;
· неравномерная сетка – в данной модели поверхность описывается в виде огромного количества отдельных точек, принадлежащих поверхности.
В данной работе в качестве модели описания поверхности (ландшафта) употребляется равномерная сетка высот. Эта модель обрисовывает координаты отдельных точек поверхности методом, показанным на рисунке:
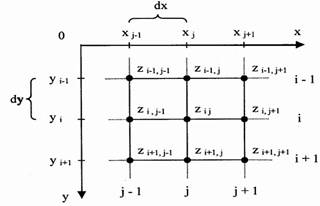
Рис. 2.1.1.1. Вид равномерной сетки высот
Любому узлу сетки с индексами (i, j) приписывается значения координат (x, y). Расстояние меж узлами однообразное – dX по оси X и dY по оси Y.
Практически таковая модель представляет собой двумерный массив, растр, матрицу, любой элемент которой сохраняет
Необходимо подчеркнуть, что не любая поверхность быть может представлена при помощи данной модели, потому что если в любом узле записывается лишь одно поверхность описывается конкретной функцией z = f(x, y). Не считая того, нереально моделирование вертикальных граней.
В случае представления ландшафта в виде равномерной сетки высот эти ограничения являются незначимыми и полностью допустимыми. Равномерная сетка нередко употребляется для описания рельефа земной поверхности [2].
Следует выделить последующие положительные черты модели равномерной сетки:
· простота описания поверхностей;
· возможность стремительно выяснить высоту хоть какой точки поверхности обычный интерполяцией.
Но эта модель также имеет и недочеты:
· для описания сложных поверхностей нужно огромное количество узлов, которое быть может ограничено объемом памяти компа;
· поверхности, которые соответствуют разноплановой функции высоты в узлах сетки, не могут моделироваться (как уже говорилось, это ограничение некординально в критериях данной работы).
Но в данной работе равномерная сетка употребляется опосредованно – сходу же при получении она разбивается на треугольники (делается ее триангуляция), так как реализация нужных в процессе работы алгоритмов машинной графики для этого примитива более ординарна. Разбиение на треугольники делается методом проведения диагонали из точки (i, j) в точку (i – 1, j + 1).
2.1.2 Выравнивание ландшафта
Построение ландшафта быть может произведено сходу опосля триангуляции равномерной сетки, но в этом случае очертания ландшафта будут резкими. Если это не нужно, то можно пользоваться способом выравнивания, реализованным в данной работе.
Его сущность заключается в последующем. В процессе выравнивания в цикле делается усреднение высот 4 примыкающих пикселей. Для повешения свойства и эффективности выравнивания, оно делается в 4 поочередных циклах – “слева вправо”, “справа влево”, “сверху вниз” и “снизу ввысь”.
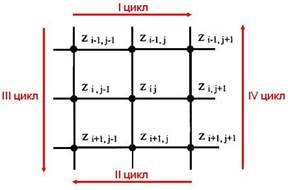
Рис. 2.1.2.1. Циклы выравнивания ландшафта
Пиксели для усреднения высот выбираются последующим образом: на K-ой итерации цикла делается усреднение высот пикселей с индексами (i – 1, j — 1), (i – 1, j), (i, j — 1) и (i, j), на (K + 1)-ой же, зависимо от номера цикла, усредняются высоты последующих пикселей:
· в I цикле – пиксели тех же 2-ух строк с индексами столбцов, увеличенными на 1;
· во II цикле – пиксели тех же 2-ух строк с индексами столбцов, уменьшенными на 1;
· в III цикле – пиксели тех же столбцов со строчными индексами, увеличенными на 1;
· в IV цикле – пиксели тех же столбцов со строчными индексами, уменьшенными на 1.
Ниже приведена иллюстрация, демонстрирующая результаты выравнивания тестового ландшафта:
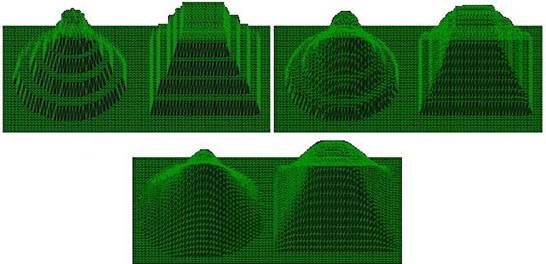
Рис. 2.1.2.2. Результаты выравнивания – без выравнивания, 1 цикл, 10 циклов.
2.1.3 Трехмерные аффинные преобразования
В процессе работы программки может возникать необходимость преобразования объектов сцены – их сдвига, масштабирования, поворота.
Для трехмерного места хоть какое аффинное преобразование быть может представлено последовательностью простых операций [3].
Ниже приводятся уравнения и матрицы преобразований:
· сдвиг точки вдоль координатных осей на dx, dy, dz:
;
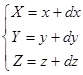
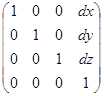· масштабирование относительно начала координат с коэффициентами kx
, ky
, kz
:
;
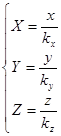
· поворот относительно осей x, y, z на угол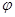 
:
o ось x:
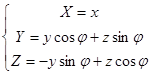
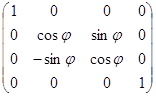
o ось y:
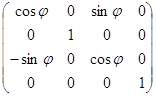
o ось z:
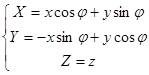
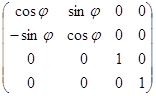
2.1.4 Проецирование
В истинное время более всераспространены устройства отображения, которые синтезируют изображение на плоскости, к примеру – мониторе. Устройства, которые делают по-настоящему большие изображения, пока довольно редки. Но все почаще возникают сведения о схожих разработках, к примеру, о больших мониторах [2].
При использовании графических устройств обычно употребляют проекции. нужно знать координаты объектов. Разглядим две системы координат. 1-ая – мировые координаты, которые обрисовывают настоящее положение объектов в пространстве с данной точностью. Иная – экранная система координат – система координат монитора, на экран которого осуществляется вывод изображения.
Пусть мировые координаты будут трехмерными декартовыми координатами. Для синтеза изображения на плоскости довольно, чудилось бы, двумерной экранной системы координат, но из-за использования метода Z-буфера (этот метод будет описан дальше), они должны быть трехмерными.
В компьютерной графике всераспространены параллельная и центральная (многообещающая) проекции.
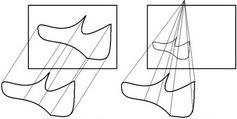
Рис. 2.1.4.1. Параллельная и центральная проекции
Для центральной проекции лучи проецирования исходят из одной точки, размещенной на конечном расстоянии от объектов и плоскости проецирования. Для параллельной проекции лучи проецирования параллельны.
В данной работе для визуализации сцены использовалась аксонометрическая (разновидность параллельной) правило, размещение плоскости проецирования задается при помощи 2-ух углов —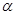 
и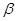 
.
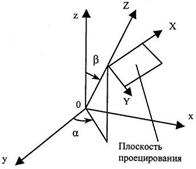
Рис. 2.1.4.2. Аксонометрическая системы координат (x, y, z) в систему (X, Y, Z). Такое преобразование быть может задано 2-мя шагами:
· поворот системы координат относительно оси z на угол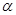 
. Таковой поворот описывается матрицей
;
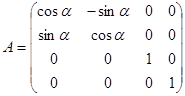· поворот новейшей системы координат (x, y, z) относительно оси x на угол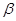 
— получение координаты (X, Y, Z). Матрица поворота:
.
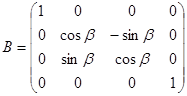Преобразование координат выражается произведением матриц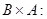 
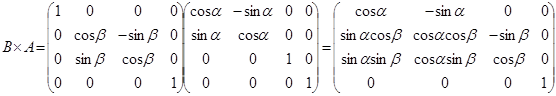
Это преобразование можно записать в формульном виде:
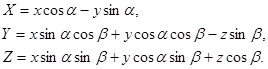
2.1.5 Отображение в окне
При формировании изображения на дисплее монитора, как уже было сказано, нужны доп преобразования, так как система координат в плоскости проецирования может не совпадать с системой координат устройства отображения.
Пусть (Xэ, Yэ, Zэ) – это экранные координаты объектов в графическом устройстве отображения. Координаты проецирования обозначим как (X, Y, Z).
Преобразование координат проекции в экранные координаты можно представить как растяжение/сжатие и сдвиг:
.
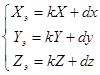Такое преобразование сохраняет пропорции объектов благодаря схожему коэффициенту растяжения/сжатия k для всех координат. Необходимо подчеркнуть, что для плоского отображения координату Z можно откинуть.
2.1.6 метод Z-буфера
Опосля получения треугольников ландшафта (триангуляции равномерной сетки) и проецирования их на экранную плоскость следует построение изображения ландшафта. В процессе его построения для удаления невидимых поверхностей употребляется метод Z-буфера.
Это один из простых алгоритмов удаления невидимых поверхностей. Работает этот метод в пространстве изображения. Мысль Z-буфера является обычным обобщением идеи о буфере кадра. Буфер кадра употребляется для запоминания атрибутов (интенсивности) всякого пикселя в пространстве изображения, Z-буфер — это отдельный буфер глубины, применяемый для запоминания координаты Z (глубины) всякого видимого пикселя в пространстве изображения. В процессе работы глубина либо значение Z всякого новейшего пикселя, который необходимо занести в буфер кадра, сравнивается с глубиной того пикселя, который уже занесен в Z-буфер. Если это сопоставление указывает, что новейший пиксель размещен впереди пикселя, находящегося в буфере кадра, то новейший пиксель заносится в этот буфер и, не считая того, делается корректировка Z-буфера новеньким значением Z. Если же сопоставление дает обратный итог, то никаких действий не делается. На самом деле, метод является поиском по x и y большего значения функции Z(x, у). Блок-схема метода смотрится последующим образом:
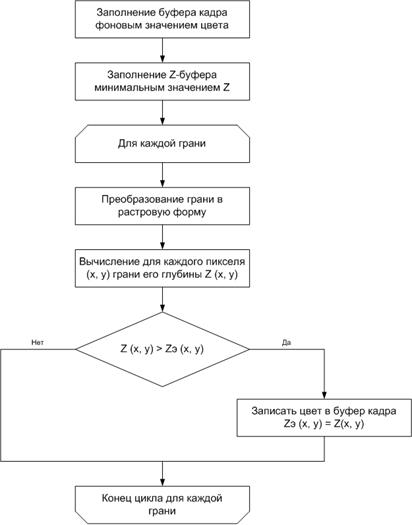
Рис. 2.1.6.1. Блок-схема метода Z-буфера
Как уже было отмечено, основное преимущество метода — его простота. Потому что габариты места изображения фиксированы, оценка вычислительной трудозатратности метода не наиболее чем линейна. Так как элементы сцены либо рисунки можно вносить в буфер кадра либо в Z-буфер в случайном порядке, их не необходимо за ранее сортировать по приоритету глубины. Потому экономится вычислительное время, затрачиваемое на сортировку по глубине, к примеру в методе художника.
Значимым недочетом метода является Потребность в значимом объеме памяти. Но в связи с тем, что стоимость оперативки повсевременно понижается, и установка доп модулей памяти на личном компе стала обычным делом, этому недочету закончили уделять особенное внимание.
Иной недочет метода Z-буфера состоит в трудозатратности устранения лестничного эффекта, также реализации эффектов прозрачности и просвечивания. Но потому что в данной работе не ставилась задачка реализации этих эффектов, то внедрение метода Z-буфера полностью обоснованно.
Математическое содержание метода заключается в последующем: если понятно уравнение плоскости, несущей любой многоугольник, то вычисление глубины всякого пикселя на сканирующей строке можно сделать пошаговым методом. Уравнение плоскости имеет вид:
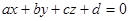
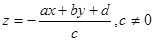
Для сканирующей строчки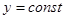
, потому глубина пикселя на данной строке, у которого 
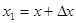, равна
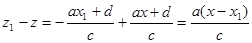
либо
,
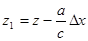но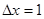 
, потому 
.
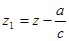Нахождение же абсцисс точек пересечения горизонтали со сторонами треугольника (это единственный вид многоугольников, применяемый при визуализации в данной работе) делается последующим образом:
· для всех сторон треугольника записываются параметрические уравнения вида
;
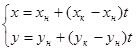· потом для каждой стороны находится параметр t при пересечении с горизонталью 
:
;
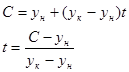· если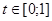 
, то рассчитывается абсцисса точки пересечения горизонтали со стороной треугольника:
.
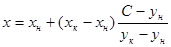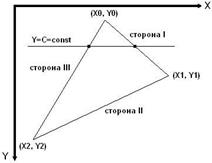
Рис. 2.1.6.2. Поиск абсцисс точек пересечения горизонтали со сторонами треугольника
2.1.7 Освещение
В любом трёхмерном приложении внедрение какой-нибудь модели освещения постоянно придаёт реалистичность обрабатываемой сцене. Как правило, в неё врубается закон, по которому рассчитывается освещённость точки в пространстве, и способ закраски освещённого многоугольника. От выбора той либо другой модели освещения зависит качество отображения, построенного компом, и скорость работы программки.
Обычно освещённость некой точки, принадлежащей грани в пространстве, складывается из рассеянной освещённости и диффузного отражения — потока света, отражающегося от поверхности объекта. Время от времени к ним добавляют зеркальное отражение — поток света, отражающийся от наружной поверхности объекта под этим же углом, под которым он падал на эту поверхность. Но в данной работе зеркальное отражение света не учитывается, потому что расчёт интенсивности зеркального отражения, к примеру по модели Фонга, просит больших вычислительных издержек. Для него требуется рассчитывать угол меж вектором наблюдения и вектором отражения и возводить косинус этого угла в некую степень, зависящую от параметров поверхности.
Диффузное отражение присуще матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой так велик, что падающий луч рассеивается неравномерно во все стороны. Таковой тип отражения характерен, к примеру, для гипса, песка, бумаги. Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла меж направлением на точечный источник света и нормалью к поверхности.
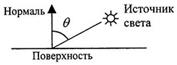
Рис. 2.1.7.1. Матовая поверхность
,
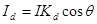где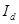 
— интенсивность источника света, 
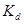— коэффициент, который учитывает характеристики материала поверхности. Интенсивность отраженного света не зависит от расположения наблюдающего.
Матовая поверхность имеет собственный цвет. Наблюдаемый цвет матовой поверхности определяется композицией собственного цвета поверхности и цвета излучения источника света (в данной работе цвет излучения источника считается белоснежным, потому учитывается лишь цвет поверхности).
Можно еще усовершенствовать модель отражения, если учитывать, что энергия от точечного источника света миниатюризируется пропорционально квадрату расстояния. Внедрение такового правила вызывает трудности, потому на практике нередко реализуют модель, выражаемую эмпирической формулой
,
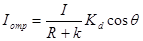где R – расстояние от источника света до рассматриваемой точки поверхности, k – случайная константа, предотвращающая деление на 0.
Для определения косинуса угла меж вектором нормали к поверхности и вектором, определяющим положение источника света в пространстве, следует пользоваться скалярным произведением. Пусть имеется вектор нормали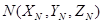 
и две точки – 
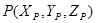, принадлежащая поверхности, и 
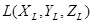, определяющая положение источника. Вектор, направленный от точки поверхности к источнику света, имеет последующие координаты: 
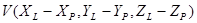. Тогда
,
,
,
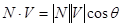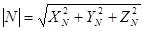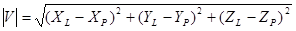либо
.
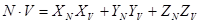Как следует
.
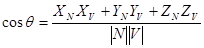Но в программке употребляются, как правило, единичные вектора нормалей, что в данном случае дозволяет уменьшить количество требуемых вычислений. В итоге:
,
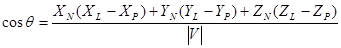либо, наиболее развернуто,
.
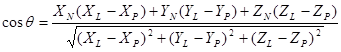Дальше рассматриваются способы закрашивания поверхности, реализованные в данной работе.
2.1.7.1 Однотонная закраска (способ гранения)
Это более обычный и требующий меньших вычислительных ресурсов способ закраски поверхности. Цвет всей поверхности рассчитывается согласно закону Ламберта. В итоге, при малом количестве граней, полиэдр смотрится конкретно как полиэдр, потому что цвета отдельных граней значительно различаются. Тем не наименее, создается эффект объемности изображения.
способ гранения дозволяет получать изображения, сравнимые по качеству с настоящими объектами, только при выполнении последующих критерий:
· источник света находится на большенном расстоянии от объекта;
· наблюдающий находится на большенном расстоянии от объекта;
· любая грань тела является гранью полиэдра, а не аппроксимирующей поверхностью;
· поверхность аппроксимирована огромным числом маленьких плоских граней.
Рис. 2.1.7.1.1. Изображение, приобретенное способом гранения
2.1.7.2 способ Гуро
Этот способ предназначен для сотворения иллюзий гладкой криволинейной поверхности, описанной в виде полиэдров либо полигональной сетки с плоскими гранями. Если любая плоская грань имеет один неизменный цвет, определенный с учетом отражения, то разные цвета примыкающих граней весьма приметны, и поверхность смотрится конкретно как полиэдр. Чудилось бы, этот недостаток можно замаскировать при помощи роста количества граней при аппроксимации поверхности, Но зрение человека имеет способность подчеркивать перепады яркости на границах смежных граней – таковой эффект именуется эффектом полос Маха. Потому для сотворения иллюзии гладкости необходимо намного прирастить количество граней, что приводит к существенному замедлению визуализации.
способ Гуро основывается на идее закрашивания плоской грани не одним цветом, а плавненько изменяющимися цветами, вычисляемыми методом билинейной интерполяции цветов примыкающих граней. Закрашивание граней по способу Гуро осуществляется в четыре шага:
· рассчитываются нормали к каждой грани;
· определяются усредненные нормали в верхушках — делается усреднение нормалей примыкающих граней. На иллюстрации приведен пример – вектор нормали в верхушке a равен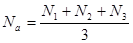 
;
·
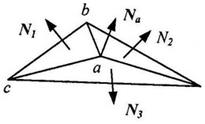
Рис. 2.1.7.2.1. Нормаль в верхушке
· на базе усредненных нормалей в верхушках рассчитываются значения интенсивностей в верхушках согласно принятой модели отражения;
· делается закрашивание грани цветом, подходящим линейной интерполяции значений интенсивности в верхушках.
Определение интерполированных значений интенсивности отраженного света в каждой точке грани (и, как следует, цвет всякого пикселя) комфортно делать во время цикла наполнения полигона (к примеру, скооперировать его с реализацией метода Z-буфера). Дальше рассматривается наполнение грани горизонталями в экранных координатах.
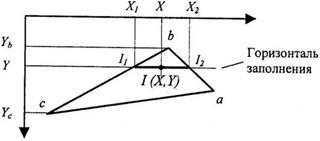
Рис. 2.1.7.2.2. Интерполяция значений интенсивности
Интерполированная интенсивность I в точке (X, Y) определяется исходя из пропорции
.
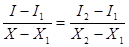Отсюда
.
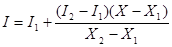значения интенсивностей I1
и I2
на концах горизонтального отрезка представляет собой интерполяцию интенсивности в верхушках:
; 
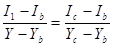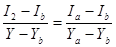либо
, 
.
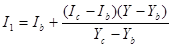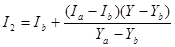Рис. 2.1.7.2.3. Изображение, получено способом Гуро
2.1.7.3 способ Фонга
Этот способ закраски аналогичен способу Гуро, но при использовании способа Фонга для определения цвета в каждой точке интерполируются не интенсивности отраженного света, а векторы нормалей.
Последовательность действий такая:
· определяются нормали к граням;
· по нормалям к граням определяются усредненные нормали в верхушках. В каждой точке закрашиваемой грани определяется интерполированный вектор нормали;
· по направлению векторов нормали определяется цвет точек грани в согласовании с принятой моделью отражения цвета.
Как уже было сказано, способ заключается в интерполяции вектора нормали. Для интерполяции будут употребляться векторы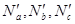 
, исходящие из начала координат плоскости проецирования и параллельными подходящим нормалям 
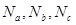в верхушках a, b и c.
Рис. 2.1.7.3.1. Интерполяция векторов нормалей
Нахождение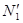 
и 
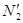делается последующим образом:
,
.
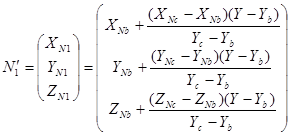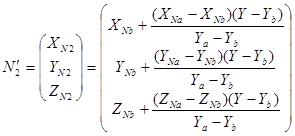где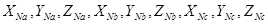 
– координаты векторов 
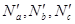. сейчас нужно отыскать координаты вектора 
:
.
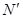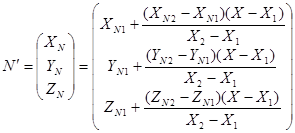Вектор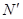 
параллелен вектору
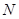для нормали в точке 
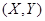, потому его можно употреблять для расчета отражения света так же, как и вектор нормали 
.
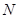Рис. 2.1.7.3.2. Изображение, приобретенное способом Фонга
2.1.7.4 анализ способов Гуро и Фонга
Способ Фонга труднее, чем способ Гуро. Для всякого пикселя поверхности нужно делать намного больше вычислительных операций. Тем не наименее, он дает наилучшие результаты, в индивидуальности при имитации зеркальных поверхностей.
Общие черты и отличия способов Фонга и Гуро можно показать на примере цилиндрической поверхности, аппроксимированной полиэдром. Пусть источник света находится за нами. Проанализируем закрашивание боковых граней.
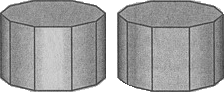
Рис. 2.1.7.4.1. Отличия закрашивания Фонга и Гуро
Ребра граней показаны черным цветом для иллюстрации особенностей закрашивания, по сути опосля закрашивания никакого каркаса не будет, и поверхность будет смотреться гладкой.
Главные отличия приметны на фронтальной грани. Она перпендикулярна направлению лучей света, потому нормали в верхушках данной грани размещаются симметрично – они образуют попарно равные по абсолютной величине углы с лучами света. Для способа Гуро это обусловливает однообразные интенсивности в верхушках фронтальной грани. А раз интенсивности однообразные, то и для хоть какой точки снутри данной грани интенсивность остается неизменной. Это обусловливает единый цвет закрашивания, а это, разумеется, некорректно.
Способ Фонга дает правильное закрашивание. Если интерполировать нормали фронтальной грани, то по центру будут интерполированные нормали, параллельные лучам света. Потому центр фронтальной грани будет светлее, чем края.
2.1.8 Последовательность действий при визуализации сцены
План действий, нужных для визуализации сцены приведен на последующей схеме:
Рис. 2.1.8.1. Схема визуализации сцены
2.2 Типы, структуры данных и функции, использованные при реализации программного комплекса
2.2.1 сходу решить, как будут представлены начальные данные, другими словами, в критериях данной работы – как будет описана карта изообластей высот и трехмерный ландшафт, какими будут форматы файлов для хранения инфы о карте и ландшафте.
В данной работе был избран полигональный метод аппроксимации пространственных фигур. Суть полигональной модели заключается в том, что каждое тело представляется в виде определенного набора граней-многоугольников, с определенной точностью приближающих форму начального тела. В качестве грани-многоугольника был избран треугольник, потому что это более обычный многоугольник, его точки постоянно лежат в одной плоскости и хоть какой наиболее непростой многоугольник можно разбить на несколько треугольников.
Разработанные типы данных и форматы файлов тщательно описаны в следующих разделах.
2.2.2 программка «Редактор карт»
2.2.2.1 Изообласти высоты
Изообласть характеризуется цветом и высотой, потому для хранения инфы о любом типе изообластей употребляется последующая запись:
THeightColor = record
Color : TRGBColor;
Height : Single;
end;
Поля данной записи имеют последующее
· Color – цвет изообласти;
· Height – представляемая высота.
Размер записи – 8 б (компилятор Delphi производит сглаживание полей в записи, потому размер записи оказывается равным 8 б, а не 7, как обязано быть).
Тип TRGBColor употребляется для хранения RGB-цвета. Представим его структуру:
TRGBColor = record
R, G, B : Byte;
end;
Размер записи – 3 б (по неведомым причинам в этом случае сглаживания не вышло).
В процессе сотворения каждой карты создается динамический массив, для хранения инфы обо всех типах изообластей:
THeightColors = array of THeightColor;
2.2.2.2 Равномерная сетка высот и ландшафт
Для хранения узлов начальной равномерной сетки (с шагом 1) употребляется динамический массив частей типа Single:
TZBitMap = array of array of Single;
Тип Single применен для экономии оперативки и дискового места, точность этого типа – 8 символов опосля запятой, что полностью довольно в рамках данной работы, при всем этом переменная этого типа занимает в памяти 4 б, в два раза меньше, чем переменная типа Real.
При триангуляции равномерной сетки создается динамический массив треугольников ландшафта. Для хранения инфы о треугольнике употребляется последующий тип данных:
TTriangle = record
P : array [0..2] of TPoint3
N : TPoint3
pD : Single;
aN : array [0..2] of TPoint3;
Color : TRGBColor;
end;
Поля данной записи имеют последующие значения:
· P – массив точек треугольника;
· N – нормаль к плоскости треугольника;
· pD – вольный член уравнения плоскости, несущей треугольник;
· aN – массив усредненных нормалей в верхушках треугольника;
· Color – базисный цвет треугольника.
Поля N и pD в совокупы образуют уравнение плоскости, несущей треугольник.
Размер записи – 92 б (настоящий размер, без сглаживания – 91 б).
нужно привести описания типов, использованных в записи TTriangle:
TPoint3 = record
X, Y, Z : Single;
end; — запись служит для хранения координат точки.
Размер записи – 12 б.
Для работы с равномерной сетью высот предусмотрены последующие процедуры и функции:
· function CreateZBitMap(Width, Height : Integer) : TZBitMap – выделение памяти для первичной сетки высот, ее размеры — Width и Height, совпадают с размерами области вывода;
· procedure FreeZBitMap(var ZBMP : TZBitMap) – освобождение памяти, занимаемой первичной сетью высот;
· function FillZBitMap(Image : TImage; Colors : THeightColors) : TZBitMap — наполнение первичной сетки высот на базе изображения, хранимого в Image и соответствий «Цвет-высота», содержащихся в массиве Colors;
· function DivideZBitMapIntoTriangles(BitMap : TZBitMap; StepX, StepY : Integer) : TTriangles – функция преобразования первичной равномерной сетки BitMap в наиболее разреженную сетку с шагами StepX и StepY по горизонтали и вертикали соответственно. Опосля этого преобразования приобретенная сетка разбивается на треугольники, на базе которых будет построен ландшафт;
· procedure SmoothMap(var BitMap : TZBitMap) – процедура для проведения 1-го цикла выравнивания первичной сетки высот;
Для работы с треугольниками ландшафта предусмотрены последующие процедуры:
· procedure FillTrianglesNormals(var Triangles : TTriangles) – расчет и наполнение всех полей записи TTriangle, не считая координат точек и цвета;
В процедуре FillTrianglesNormals употребляются последующие вспомогательные функции:
· function GetNormal(T : TTriangle) : TPoint3 – процедура для вычисления координат вектора нормали к плоскости треугольника;
· function CorrectNormal(N : TPoint3) : TPoint3 – процедура нормализации вектора нормали;
· procedure AddNormal(var N : TPoint3; NAdd : TPoint3; var Count : Integer), procedure DivideNormal(var N : TPoint3; Count : Integer) – эти процедуры в совокупы служат для вычисления усредненной нормали в верхушке треугольника;
2.2.2.3 Тип и структура файла для хранения карт изообластей
файл для хранения инфы о разметке карты изообластей высот является текстовым. Он имеет расширение HCL и разбит на секции, разбитые строчками–маркерами. Ниже приведена его структура:
· заголовок файла – строчка ‘Landscape heights map’;
· заголовок секции высот – строчка ‘[ColorHeights Start]’;
o последовательность записей типа THeightColor;
· окончание секции высот – строчка ‘[ColorHeights End]’;
· заголовок секции пикселей – строчка ‘[Pixels Start]’;
o ширина и высота карты в пикселях;
o информация о пикселях карты, сжатая при помощи способа группового кодировки (последовательность пар «Индекс цвета – Длина участка»);
· окончание секции пикселей – строчка ‘[Pixels End]’;
способ группового кодировки употребляется для экономии дискового места, занимаемого файлами плоских карт. Сущность способа заключается в том, что сохраняется информация не о любом пикселе карты, а о группах пикселей, принадлежащих одной строке и имеющих общий цвет (запоминается длина участка и цвет его пикселей). Таковым образом, можно достигнуть значимой экономии дискового места. Это можно проверить, сопоставив размер файла BMP, хранящего изображение карты, и размер соответственного ему файла HCL. Но экономия дискового места не постоянно быть может достигнута при использовании данного способа. Можно привести таковой пример изображения, при кодировке которого размер итогового файла будет превосходить размер начального BMP-файла. Строчки этого изображения должны состоять из таковых пикселей, что цвет всех 2-ух примыкающих не совпадает. Но, невзирая на это, внедрение способа группового кодировки в данной работе полностью оправдано, потому что карта в общем случае имеет полностью однородную структуру.
Для работы c файлами карт изообластей высот предусмотрены последующие процедуры:
· procedure LoadFromHeightsMap(FileName : string; var Image : TImage; var Colors : THeightColors) — процедура для загрузки из файла HCL карты изообластей высот и соответствий цвет-высота. Информация загружается из файла FileName. Разметка карты выводится на Image, а соответствия «Цвет-высота» помещаются в динамический массив Colors;
· procedure SaveAsHeightsMap(Image : TImage; Colors : THeightColors; FileName : string) – процедура для сохранения разметки карты в файл HCL. Разметка считывается из Image, соответствия «Цвет-высота» из массива Colors, эта информация помещается в файл c именованием FileName.
2.2.2.4 Распределение программки по модулям
Таблица 2.2.2.4.1. Распределение программки «Редактор карт» по модулям
имя модуля
Описанные типы
Предназначение модуля
AboutUnit.pas
—
Модуль формы «О программке»
ColorUnit.pas
—
Модуль формы определения соответствия «Цвет-высота»
HelpUnit.pas
—
Модуль формы «Помощь»
MainUnit.pas
—
Основной модуль программки
ME_ExtRegUnit.pas
—
Модуль регистрации расширения HCL
ME_FileUnit.pas
—
Модуль работы с файлами
ME_GraphicsUnit.pas
—
Модуль реализации процедур визуализации
ME_MathUnit.pas
TRGBColor, TPoint3, TTriangle, TTriangles, THeightColor, THeightColors, TZBitMap
Модуль реализации вычислений
MLEditorUnit.pas
—
Модуль инструментальной формы «Обработка карт»
NewPictureUnit.pas
—
Модуль формы определения размеров новейшей карты
SectionUnit.pas
—
Модуль формы «Разрез»
2.2.2.5 Связи меж модулями программки
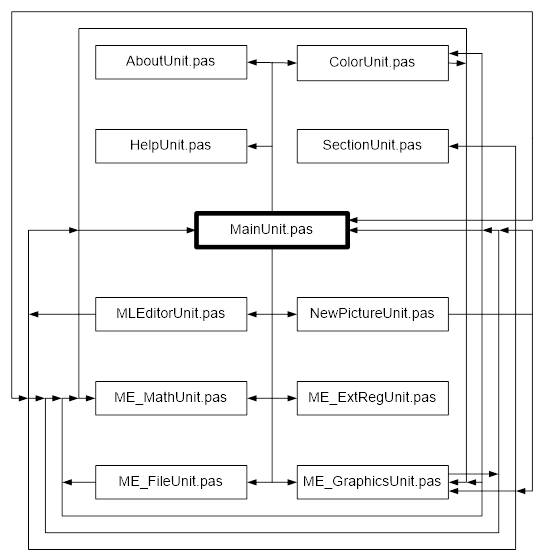
Рис. 2.2.2.5.1. Связи меж модулями программки «Редактор карт»
2.2.3 программка «Просмотр ландшафта»
В программке «Просмотр ландшафта» также употребляется тип TTriangle. Он стопроцентно аналогичен типу TTriangle, применяемому в программке «Редактор карт». Ландшафт, как уже говорилось, представляется как совокупа треугольников, потому для его хранения в программке предусмотрен тип, представляющий из себя динамический массив:
TTriangles = array of TTriangle.
2.2.3.1 Процедуры манипуляции изображением ландшафта
Сначала работы программки, при загрузке ландшафта из файла, должны быть выполнены некие предварительные деяния, а именно, вычисление масштаба и экранных смещений для вывода изображения ландшафта. Для этого предусмотрена функция
· function GetScale(Triangles : TTriangles; Width, Height : Integer) : Single;
нужно объяснить значения аргументов представленной функции:
Triangles – треугольники ландшафта;
Width, Height – размеры области вывода.
Для внедрения вычисленного масштаба и экранных смещений к треугольникам ландшафта служит функция
· function MulTrianglesScale(Triangles : TTriangles; dX, dY : Integer; Scale : Real) : TTriangles;
значения аргументов:
Triangles – начальные треугольники сцены;
dX, dY – экранные смещения по горизонтали и по вертикали;
Scale – коэффициент масштабирования.
В процессе работы с приобретенным изображением может возникать необходимость его вращения относительно координатных осей. Для этих целей введены 3 группы функций, разбитых по уровням абстракции:
· function RotatePointX(P, Center : TPoint3; Alpha : Real) : TPoint3;
· function RotatePointY(P, Center : TPoint3; Alpha : Real) : TPoint3;
· function RotatePointZ(P, Center : TPoint3; Alpha : Real) : TPoint3;
· function RotateTriangleX(T : TTriangle; Center : TPoint3; Alpha : Real) : TTriangle;
· function RotateTriangleY(T : TTriangle; Center : TPoint3; Alpha : Real) : TTriangle;
· function RotateTriangleZ(T : TTriangle; Center : TPoint3; Alpha : Real) : TTriangle;
· function RotateTrianglesX(Triangles : TTriangles; Center : TPoint3; Alpha : Real) : TTriangles;
· function RotateTrianglesY(Triangles : TTriangles; Center : TPoint3; Alpha : Real) : TTriangles;
· function RotateTrianglesZ(Triangles : TTriangles; Center : TPoint3; Alpha : Real) : TTriangles;
Аргументы всех функций однотипны: 1-ый – объект, который должен быть повернут, 2-ой – центр поворота; 3-ий – угол поворота.
2.2.3.2 Z-буфер
При визуализации ландшафта употребляется Z-буфер. Для его хранения употребляется тип, представляющий из себя динамический массив:
TBuffer = array of array of Single.
Для работы с Z-буфером употребляются последующие процедуры:
· procedure CreateBuffer(out Buffer : TBuffer) – процедура для выделения памяти для Z-буфера;
· procedure ClearBuffer(var Buffer : TBuffer) – чистка буфера – его наполнение наименьшим значением глубины;
· procedure FreeBuffer(var Buffer : TBuffer) – освобождение памяти, занимаемой буфером.
2.2.3.3 Буфер кадра
Не считая того, нужен и буфер кадра. Буфер кадра в данной работе представлен статическим массивом (это ограничение обосновано внедрением функции BitBlt, обеспечивающей резвый вывод изображения):
sWidth = 500;
sHeight = 650;
TScreen = array [0..sWidth — 1, 0..sHeight — 1] of Integer.
Перед выводом еще одного кадра буфер кадра должен быть очищен. Для этого предназначена процедура
· procedure ClearScreenBuffer;
2.2.3.4 Процедуры визуализации ландшафта
Для визуализации треугольников ландшафта и ландшафта в целом предусмотрены последующие процедуры:
· procedure FillTriangleNormal (T : TTriangle; var Buffer : TBuffer; dX, dY : Integer; Scale : Real; LightPos : TPoint3) – закрашивание треугольника T способом гранения. Употребляется Z-буфер Buffer, употребляются экранные смещения dX и dY, коэффициент масштабирования Scale, положение источника света задается точкой LightPos;
· procedure FillTriangleGouraud(T : TTriangle; var Buffer : TBuffer; dX, dY : Integer; Scale : Real; LightPos : TPoint3) – процедура, реализующая способ закраски Гуро. Аргументы подобны аргументам предшествующей процедуры;
· procedure FillTrianglePhong(T : TTriangle; var Buffer : TBuffer; dX, dY : Integer; Scale : Real; LightPos : TPoint3) – процедура, реализующая способ закраски Фонга. Аргументы подобны аргументам предшествующей процедуры;
· procedure DrawLightSource(P : TPoint3; dX, dY : Integer; Scale : Real; Buffer : TBuffer) – процедура для вывода окружности (по методу Брезенхема), обозначающей положение источника света. Положение источника цвета задается точкой P. Другие характеристики подобны характеристикам прошлых функций;
· procedure DrawLine(S, E : TPoint; Color : TRGBColor) – процедура вывода полосы по методу ЦДА. Аргументы S и E – точки начала и конца отрезка, Color описывает цвет отрезка;
· procedure DrawTriangle(T : TTriangle) – вывод каркаса треугольника в буфер кадра;
· procedure DrawWireTriangles(Triangles : TTriangles; dX, dY : Integer; Scale : Real) – вывод треугольников ландшафта в каркасном режиме;
· procedure DrawSolidTriangles(Triangles : TTriangles; var Buffer : TBuffer; dX, dY : Integer; Scale : Real; Light : TLightType; LightPos : TPoint3; ShowLightSource : boolean) – вывод треугольников ландшафта в режиме сплошной закраски. характеристики процедуры:
o Triangles – треугольники ландшафта;
o Buffer – Z-буфер, применяемый при визуализации;
o dX, dY – экранные смещения по горизонтали и вертикали;
o Scale – коэффициент масштабирования;
o Light – описывает способ закраски треугольников. TLightType — перечисляемый тип, он определяется последующим образом:
TLightType = (Normal, Gouraud, Phong);
o LightPos – точка, задающая положение источника света;
o ShowLightSource – логическая переменная, определяющая, отображается ли источник света;
· procedure DrawScene(Triangles : TTriangles; View : TViewType; Light : TLightType; LightPos : TPoint3; ShowLightSource : boolean; var Buffer : TBuffer; dX, dY : Integer; Scale : Real; DC : Integer; NHDC : HDC; HBMP : HBITMAP) – основная процедура, объединяющая внутри себя все способы м режимы вывода сцены.
Аргументы, которые не были описаны в процедуре DrawSolidTriangles:
o View – переменная определяющая режим отображения треугольников — каркасный либо сплошной. TViewType – перечисляемый тип, его описание — TViewType = (Wire, Solid);
o DC, NHDC, HBMP – переменные, применяемые при выводе изображения при помощи функции BitBlt.
2.2.3.2 Тип и структура файла для хранения ландшафта
Файлы, применяемые для хранения инфы о треугольниках ландшафта, имеют расширение LND и являются типизированными. Был избран конкретно этот тип файлов, потому что внедрение текстовых файлов существенно замедлило бы процесс загрузки ландшафтов, а для работы с нетипизированными файлами пришлось бы разрабатывать сложные процедуры ввода/вывода (на базе доступных процедур низкого уровня для работы с файлами), в то время как прирост производительности был бы незначимым.
В программке файлы ландшафтов описываются последующим образом: File of TTriangle;
Для работы с файлами ландшафта предусмотрена последующая функция:
function LoadTrianglesFromFile(FileName : string) : TTriangles;
Единственный ее аргумент — название файла, из которого будет считываться информация о треугольниках ландшафта.
2.2.3.3 Распределение программки по модулям
Таблица 2.2.3.3.1. Распределение программки «Просмотр ландшафта» по модулям
имя модуля
Описанные типы
Предназначение модуля
AboutUnit.pas
—
Модуль формы «О программке»
HelpUnit.pas
—
Модуль формы «Помощь»
L_ExtRegUnit.pas
—
Модуль регистрации расширения LND
L_FileUnit.pas
—
Модуль работы с файлами
L_GraphicsUnit.pas
TBuffer, TScreen, TViewType, TLightType
Модуль реализации процедур визуализации
L_MathUnit.pas
TRGBColor, TPoint3, TTriangle, TTriangles
Модуль реализации вычислений
LandscapePositionUnit.pas
—
Модуль формы «Положение ландшафта»
LightParamsUnit.pas
—
Модуль формы «Характеристики источника света»
MainUnit.pas
—
Основной модуль программки
StatisticsUnit.pas
—
Модуль формы «Статистика»
ViewParamsUnit.pas
—
Модуль формы «Зрительные характеристики»
2.2.3.4 Связи меж модулями программки
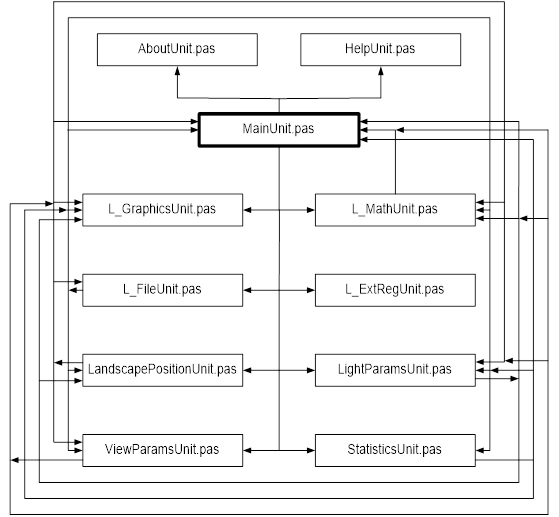
Рис. 2.2.3.4.1. Связи меж модулями программки «Просмотр ландшафта»
3. Технологическая часть
3.1 Выбор языка программирования
При разработке программного комплекса употреблялся язык программирования высочайшего уровня Object Pascal в составе среды зрительного программирования Borland Delphi 7.
Выбор был остановлен конкретно на этом языке программирования, потому что он дозволяет создавать программки с точной модульной организацией, позволяющей реализовывать серьезное разделение уровней абстракции. Не считая того, среда Delphi предоставляет программеру необъятную библиотеку зрительных компонент, позволяющих создавать высококачественный интерфейс случайной трудности.
3.2 Описание программного комплекса
В состав программного комплекса входят два приложения: «Редактор карт» и «Просмотр ландшафта».
3.2.1 программка «Редактор карт»
3.2.1.1 Общие сведения
Программка “Редактор карт” служит для сотворения ландшафтов на базе плоских карт изообластей. Данные карты могут быть сделаны при помощи средств редактирования, предоставляемых “Редактором карт” либо загружены в редактор из BMP-файлов (требуемая глубина цвета — 24 бита).
Получаемые карты хранятся в файлах с расширением HCL. Файлы этого типа являются текстовыми, они содержат информацию о цветах, использованных для задания изообластей, о высотах, соответственных перечисленным цветам, также конкретно о разметке карты. При всем этом для записи пикселей карты употребляется групповое кодирование.
3.2.1.2 интерфейс программки
При запуске программки на дисплее возникает основная и инструментальная формы.
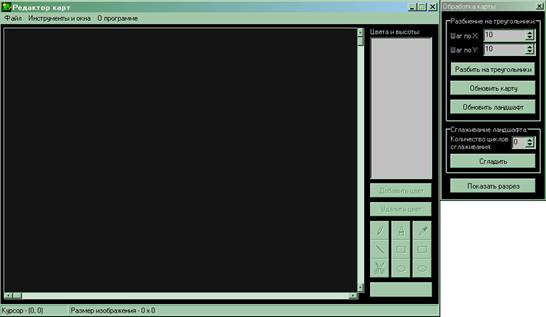
Рис. 3.2.1.2.1. Формы, отображаемые при запуске «Редактора карт»
основное меню программки содержит последующие подменю:
1)
файл:
· Сделать — сделать новейшую карту;
· Открыть — открыть уже существующую карту при помощи специального диалога;
· Сохранить — сохранить текущую карту в файл;
· Выход — закончить работу с программкой;
2)
Инструменты и окна:
· Обработка карты — описывает видимость инструментальной формы «Обработка карты»;
· Запустить «Просмотр ландшафта» — запускает приложение «Просмотр ландшафта», в которое загружается ландшафт, соответственный текущей карте;
· Зарегистрировать собственное расширение — зарегистрировать в реестре расширение HCL, что даст возможность открывать файлы данного типа двойным щелчком мыши;
· Отменить регистрацию расширения — удалить из реестра информацию о расширении HCL;
3)
О программке:
· О программке — вывод формы с некой информацией о данной программке;
· Помощь — вывод справочной инфы о программке.
Справа от неких пт меню указаны сочетания кнопок, реализующие деяния, надлежащие данному пт меню.
3.2.1.2.1 Инструментальная форма «Обработка карты»
Рис. 3.2.1.2.1.1. Инструментальная форма «Обработка карты»
Плоская карта, редактируемая и создаваемая при помощи «Редактора карт» представляет собой совокупа изообластей высот. Для задания этих областей употребляются соответствия «цвет-Высота», другими словами карте, размеченной цветами, соответствует bitmap высот, любая точка которого характеризуется высотой. Для сотворения трехмерного ландшафта на базе плоской карты, bitmap высот разбивается на треугольники с неким данным шагом, другими словами ландшафт состоит из трехмерных треугольников.
Шаг разбиения на треугольники по горизонтали и вертикали задается при помощи полей ввода «Шаг по X» и «Шаг по Y». Единица измерения этих величин — пиксель.
Клавиша «Разбить на треугольники» служит для вывода плоских треугольников разбиения на карту.
Клавиша «Обновить карту» удаляет с карты выведенные треугольники.
Клавиша «Обновить ландшафт» создана для сотворения bitmap’а высот и, на его базе, с данными шагами разбиения, — ландшафта.
Группа «Выравнивание ландшафта» дозволяет сгладить ландшафт — придать его очертаниям огромную плавность.
Клавиша «Показать разрез» выводит специальную форму, на которой отображается разрез ландшафта вертикальной плоскостью, данной ранее на карте прямой.
3.2.1.2.2 Инструменты главной формы
Огромную часть главной формы занимает область рисования, которая показывает и дозволяет редактировать карту.
Если создается новенькая карта, то поначалу нужно задать соответствия «цвет-высота», это делается при помощи клавиши «Добавить цвет» либо нажатия клавиши Insert, когда фокус ввода находится на перечне цветов. Опосля выполнения этих действий возникает форма «Определение цвета«, которая дозволяет добавлять либо редактировать имеющиеся соответствия «цвет-высота». Перечень цветов содержит информацию о имеющихся соответствиях. Его элементы можно удалять при помощи клавиши «Удалить цвет» либо нажатия клавиши Delete, когда фокус ввода находится на перечне. При удалении, области, занимаемые удаляемым цветом, заполняются цветом нулевой высоты.
Для редактирования карты служат последующие инструменты:
· «Карандаш» — дозволяет чертить произвольные кривые;
· «Кисть» — наполнение областей карты;
· «Отрезок»;
· «Контурный прямоугольник»;
· «Заполненный прямоугольник»;
· «Контурный эллипс»;
· «Заполненный эллипс».
Рисование этих примитивов осуществляется при помощи мыши при удерживаемой левой кнопочке. цвет рисуемых примитивов определяется при помощи перечня цветов и отображается на специальной панели в нижнем правом углу формы.
Не считая обрисованных, есть также последующие инструменты:
· «Ножницы» — для задания на карте прямой, определяющей вертикальную плоскость сечения. Просмотр сечений дозволяет получать определения цвета случайного пикселя на карте.
3.2.1.3 Работа программки
3.2.1.3.1 Требования к расположению файлов программки
Исполняемый файл программки — MapEditorProj.exe. В папке, где расположен этот файл обязана находиться пиктограмма HCL_Icon.ico. Эта пиктограмма будет нужно при регистрации расширения HCL — она будет присвоена файлам с сиим расширением. Не считая того, в главный папке MapEditorProj обязана находиться программка LandscapeProj, т.к. в неприятном случае будет невозможна их Интеграция. Лучше наличие в главный папке программки каталогов ScreenShots и Landscapes. В каталоге ScreenShots будут помещаться сохраненные изображения ландшафтов (в формате BMP, размер всякого файла ~ 1.23 МБ), создаваемые программкой «Просмотр ландшафта». В каталоге Landscapes предполагается хранение файлов ландшафтов(*.lnd) и плоских карт(*.hcl), на базе которых строятся ландшафты.
3.2.1.3.2 Создание карт
Сделать карту изообластей можно 2-мя методами:
· загрузить уже имеющееся изображение в формате BMP (поддерживается работа лишь с 24-битным цветом). В этом случае программка автоматом выделит все имеющиеся на изображении цвета и расположит их в перечень. Дальше остается лишь задать в соответствие цветам высоты, т.к. по дефлоту присваивается
· сделать новейшую карту и разметить ее без помощи других, добавляя соответствия по собственному желанию. Создание новейшей карты начинается с возникновения формы «характеристики изображения», которая дозволяет задать размер создаваемой карты.
3.2.1.3.3 Сохранение карт
Сохранение делается при помощи специального диалога, в каком обусловятся путь сохранения файлов. При сохранении создаются 3 файла:
· карта изообластей *.hcl;
· ландшафт *.lnd;
· *.bmp с изображением приобретенной карты.
3.2.1.3.4 Открытие карт
Вероятна загрузка 2-ух типов файлов — BMP и HCL. Загрузка может происходить 3-мя методами:
· через диалог открытия в самой программке;
· двойным щелчком по файлу (лишь для HCL-файлов опосля регистрации этого расширения);
· методом перетаскивания файла на форму приложения c помощью мыши.
3.2.2 программка «Просмотр ландшафта»
3.2.2.1 Общие сведения
Программка «Просмотр ландшафта» предназначена, как надо из ее наименования, для просмотра ландшафтов, создаваемых на базе карт изообластей, при помощи программки «Редактор карт».
3.2.2.2 интерфейс программки
При запуске программки на дисплее возникает основная и инструментальная формы.
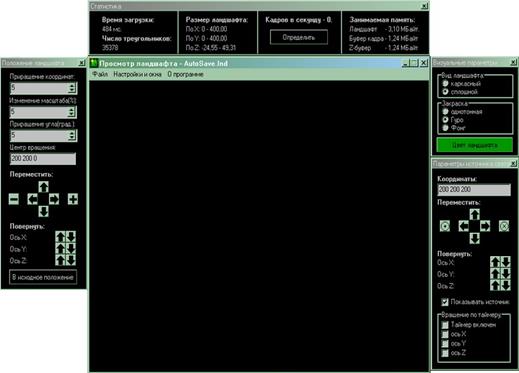
Рис. 3.2.2.2.1. Формы, отображаемые при запуске «Просмотра ландшафта»
основное меню программки содержит последующие подменю:
1) файл:
· Открыть — загрузить ландшафт при помощи диалога открытия файлов;
· Выход — закончить работу с программкой;
2) Опции и окна:
· Положение ландшафта — описывает видимость инструментальной формы «Положение ландшафта»;
· Зрительные характеристики — видимость формы «Зрительные характеристики»;
· характеристики источника света — видимость формы «характеристики источника света»;
· Статистика — видимость формы «Статистика»;
· Сохранить изображение — сохранить текущее изображение загруженного ландшафта в виде графического файла, помещаемого в папку ScreenShots, расположенную в главном каталоге программки;
· Зарегистрировать собственное расширение — зарегистрировать в реестре расширение LND, что даст возможность открывать файлы данного типа двойным щелчком мыши;
· Отменить регистрацию расширения — удалить из реестра информацию о расширении LND;
3) О программке:
· О программке — вывод формы с некой информацией о данной программке;
· Помощь — вывод справочной инфы о программке.
Справа от неких пт меню указаны сочетания кнопок, реализующие деяния, надлежащие данному пт меню.
3.2.2.2.1 Инструментальная форма «Положение ландшафта»
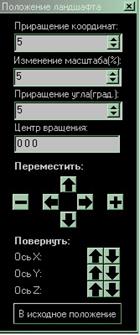
Рис. 3.2.2.2.1.1. Инструментальная форма «Положение ландшафта»
Данная форма создана для управления положением ландшафта в пространстве. Она содержит последующие элементы управления:
· поле ввода «Приращение координат» — создано для задания величины шага перемещения ландшафта в экранной системе координат;
· поле ввода «Изменение масштаба» — задание величины процентного конфигурации коэффициента масштабирования;
· поле ввода «Приращение угла» — задание величины шага поворота ландшафта (задается в градусах);
· поле ввода «Центр вращение» — ввод 3-х координат центра вращения ландшафта в системе координат ландшафта;
· клавиши группы «Переместить» предусмотрены для перемещения и масштабирования ландшафта. Эти же деяния можно делать при помощи мыши либо клавиатуры. мышь: перемещение осуществляется при удерживаемой клавише Shift, для масштабирования употребляется колесико мыши; клавиатура: стрелочные клавиши для перемещения, клавишиactiveXдля масштабирования;
· клавиши группы «Повернуть» употребляются для вращения ландшафта относительно соответственных осей. Вращение ландшафта также может выполняться при помощи мыши либо клавиатуры. мышь: горизонтальное смещение — поворот относительно оси Z, вертикальное — относительно X, горизонтальное с удерживаемой кнопкой Alt — относительно Y; клавиатура: относительно X — Insert и Delete, Y — Home и End, Z — PageUp и PageDown;
· клавиша «В начальное положение» создана для возврата ландшафта и источника света в то положение, в каком они находились конкретно опосля загрузки.
3.2.2.2.2 Инструментальная форма «Зрительные характеристики»
Рис. 3.2.2.2.21. Инструментальная форма «Зрительные характеристики»
Эта форма создана для выбора способов и характеристик визуализации ландшафта. Для этого служат последующие элементы интерфейса:
· группа «Вид ландшафта» дозволяет избрать способ построения ландшафта;
· группа «Закраска» описывает способ визуализации треугольников ландшафта;
· панель «цвет ландшафта» описывает базисный цвет ландшафта. Выбор цвета осуществляется при помощи диалога, вызываемого щелчком по панели.
3.2.2.2.3 Инструментальная форма «Характеристики источника света»
Рис. 3.2.2.2.3.1. Инструментальная форма «Характеристики источника света»
Данная форма создана для управления источником света. Находятся последующие элементы интерфейса:
· поле ввода «Координаты» дозволяет задавать координаты источника света в системе координат ландшафта;
· клавиши группы «Переместить» предусмотрены для переноса источника света вдоль соответственных осей. Употребляется приращение координат, данное на форме «Положение ландшафта». Перемещение источника может быть также и при помощи мыши и клавиатуры. мышь (с удерживаемой кнопкой Ctrl): горизонтальное перемещение — перемещение вдоль X, вертикальное — вдоль Y; клавиатура (при удержании Ctrl): стрелочные клавиши — перемещение вдоль соответственных осей, клавишиactiveXи ‘-‘ — вдоль оси Z,
· клавиши группы «Повернуть» разрешают вращать источник света относительно соответственных осей. Употребляется приращение угла с формы «Положение ландшафта». Вращение источника света предвидено также и при помощи клавиатуры (при удержании Ctrl): клавиши Insert и Delete, Home и End, Page Up и Page Down — вращение относительно осей X, Y и Z соответственно;
· переключатель «Демонстрировать источник» описывает видимость источника света. Он схематично изображается в виде желтоватого кружочка. Кружочек сплошной, если источник находится меж наблюдателем и ландшафтом, в неприятном случае он контурный;
· группа «Вращение по таймеру» дозволяет инициировать вращение источника света относительно избранных осей по таймеру;
3.2.2.2.4 Инструментальная форма «Статистика»
Рис. 3.2.2.2.4.1. Инструментальная форма «Статистика»
Эта форма содержит информацию о программке и текущем ландшафте. А именно, опосля загрузки ландшафта на нее выводится информация о времени загрузки (в миллисекундах), числе треугольников ландшафта, его линейных размерах (в пикселях), также о распределении памяти для хранения ландшафта, Z-буфера, буфера кадра.
Клавиша «Найти» дозволяет найти число кадров вывода ландшафта, рассчитываемых и выводимых за 1 секунду.
3.2.2.3 Работа программки
3.2.2.3.1 Требования к расположению файлов программки
Исполняемый файл программки — LandscapeProj.exe. В папке, где расположен этот файл, обязана находиться пиктограмма LND_Icon.ico. Эта пиктограмма будет нужно при регистрации расширения LND — она будет присвоена файлам с сиим расширением. Другие требования подобны описанным в Разделе, касающемся программки “Редактор карт”.
3.2.2.3.2 Открытие файлов ландшафтов
Открытие файлов *.lnd может быть 3-мя методами:
· конкретно через меню программки при помощи специального диалога;
· двойным щелчком по файлу ландшафта (опосля регистрации расширения);
· методом перетаскивания файла на форму приложения. Опосля открытия файла просмотр ландшафта осуществляется при помощи уже обрисованных инструментальных форм.
3.2.3 Системные требования
Системные требования программного комплекса создаются основным образом приложением «Просмотр ландшафта», потому что оно намного наиболее требовательно к системным ресурсам, чем «Редактор карт». Они таковы:
· операционная система Windows 98/Me/2000/XP/2003 Server;
· машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) (либо вычислительной системы) которое делает арифметические и логические операции данные программкой преобразования инфы управляет вычислительным действием и коор c тактовой частотой 400 МГц;
· размер оперативки 64 МБ;
· видеоплата, обеспечивающая графическое разрешение 1024×768 и глубину цвета 24 бита;
· 35 МБ дискового места.
4. Экспериментально-исследовательская часть
Тестирование проводилось на компе Pentium IV — 2.67 GHz/768 Mb/GeForce4 MX-440, AGP 8x, DDR 128 Mb.
Были проведены последующие исследования:
1) исследование временных черт алгоритмов закраски – для 3 реализованных в работе алгоритмов были произведены исследования зависимости скорости работы от числа треугольников ландшафта;
2) исследование временных черт загрузки разных типов LND-файлов (текстового и типизированного);
3) исследование результатов использования способа группового кодировки при разработке HCL-файлов.
В качестве испытательной карты в исследовательских работах № 1 и 2 была взята карта “Алтай.hcl”. Размеры карты “Алтай.hcl”: 430x409x39 пикселей (X x Y x Z).
4.1. исследование № 1
Условия теста: в «Редактор карт» была загружена избранная карта, дальше, с изменяемым от 1 до 20 пикселей, шагом разбиения карты, строились ландшафты. Во время тестов никаких манипуляций с изображением ландшафта не выполнялось – оно оставалось в том положении, в каком находилось конкретно опосля загрузки. Результаты теста приведены в таблице:
Таблица 4.1.1. Результаты исследования № 1
способ закраски и
число кадров за секунду
Число
треугольников ландшафта
Шаг разбиения
(X x Y)
Однотонная
Гуро
Фонг
3
3
3
350064
1 x 1
8
7
6
87720
2 x 2
12
11
9
38896
3 x 3
17
15
10
22032
4 x 4
21
18
12
14104
5 x 5
24
21
12
9792
6 x 6
27
23
13
7316
7 x 7
30
25
14
5508
8 x 8
33
27
14
4416
9 x 9
35
28
14
3526
10 x 10
37
29
15
2964
11 x 11
39
30
15
2448
12 x 12
40
31
15
2112
13 x 13
41
32
15
1860
14 x 14
42
32
15
1624
15 x 15
43
33
16
1404
16 x 16
44
34
16
1248
17 x 17
46
35
16
1104
18 x 18
46
35
16
1012
19 x 19
49
36
16
924
20 x 20
Для большей наглядности приведем графики зависимости числа кадров, обрабатываемых за 1 секунду, от шага разбиения и числа треугольников ландшафта:
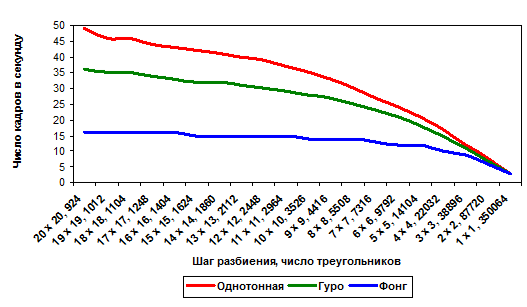
Рис. 4.1.1. Результаты исследования № 1
Из приведенных выше таблицы и диаграммы можно создать последующие выводы:
· повышение числа треугольников ландшафта вызывает уменьшение числа кадров, обрабатываемых за 1 секунду;
· закраска по Фонгу просит больших вычислительных ресурсов по сопоставлению со всеми остальными способами, в тоже время скорость ее работы меньше всего зависит от числа треугольников ландшафта;
· при увеличении числа треугольников ландшафта разница в скорости работы рассмотренных алгоритмов миниатюризируется. Когда карта разбивается на треугольники с шагом 1 x 1, различие меж методами становится наименьшим – как по скорости работы, так и по качеству получаемого изображения (однотонная закраска смотрится наименее отменно, чем закраска Фонга и Гуро).
4.2. исследование № 2
При разработке программного комплекса формат файла LND (для хранения инфы о треугольниках ландшафта) изменялся. На исходной стадии разработки эти конфигурации касались лишь прибавления новейших полей в записи, хранимые в файле, тип файла был текстовым. Но равномерно карты ландшафтов, разрабатываемых в «Редакторе карт», становились все наиболее сложными, они добивались все большей детализации. Потому росли объемы LND-файлов, При всем этом время загрузки существенно увеличивалось и становилось совсем неудовлетворительным. В итоге было принято решение поменять тип LND-файла, создать его типизированным. Опосля этого время загрузки LND-файлов в «Просмотр ландшафта» существенно сократилось. Следует увидеть, что скорость записи инфы в текстовый и типизированный файлы фактически не различается. Ниже приведены временные свойства загрузки текстовых и типизированных LND-файлов.
Таблица 4.2.1. Результаты исследования № 2
Шаг разбиения (X x Y)
Тип LND-файла
Текстовый
Типизированный
Размер файла
(Мб)
время загрузки (с)
Размер файла (Мб)
Время загрузки (с)
1 x 1
0,113
1,469
0,310
0,016
2 x 2
0,140
2,657
0,390
0,016
3 x 3
0,175
4,609
0,480
0,031
4 x 4
0,233
7,140
0,640
0,047
5 x 5
0,313
10,828
0,860
0,047
6 x 6
0,451
19,515
1,240
0,078
7 x 7
0,704
46,968
1,930
0,125
8 x 8
1,210
157,812
3,410
0,187
9 x 9
2,740
662,781
7,700
0,437
10 x 10
10,90
4102,093
30,71
1,922
Для большей наглядности построены графики зависимости времени загрузки файла от его размера:
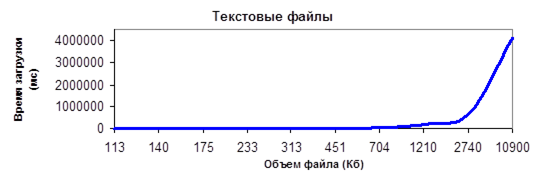
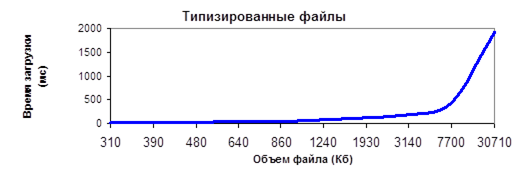
Рис. 4.2.1. Результаты исследования № 2
Из проведенного исследования можно создать последующие выводы:
· время загрузки ландшафта из текстового файла существенно больше времени загрузки из типизированного файла (при малых размерах файлов это различие составляет 10-ки раз, при увеличении размеров оно добивается тыщ (!!!) раз);
· такое отличие времени загрузки, разумеется, разъясняется неизменным преобразованием инфы из символьного представления в числовое (работой функций Val либо StrToFloat) при загрузке из текстового файла, в то время как при чтении из типизированного файла такового преобразования не требуется;
· внедрение типизированных файлов стопроцентно оправдано за счет колоссального роста скорости загрузки ландшафтов, даже невзирая на практически троекратное повышение размера получаемых LND-файлов.
4.3 исследование № 3
Как уже говорилось, при разработке HCL-файлов, хранящих информацию о разметке карт, употребляется способ группового кодировки. Этот способ уже был описан выше, потому в данном разделе будет приведена информация, доказывающая эффективность использования способа, и выяснена степень данной эффективности.
Демонстрация результатов использования способа была проведена на последующем наборе карт (размеры приведены в пикселях):
· Австралия.hcl (500 x 395);
· Алтай.hcl (430 x 409);
· Африка.hcl (700 x 730);
· Несжимаемый.hcl (200 x 200);
· тест выравнивания.hcl (400 x 200);
· Южная Америка.hcl (735 x 1125).
Ниже приведена таблица, которая дозволила бы узнать степень сжатия изображения при использовании способа группового кодировки:
Таблица 4.3.1. Результаты исследования № 3
Заглавие карты
размеры карты
(пиксели)
Размер BMP-файла
(Кб)
Размер HCL-файла
(Кб)
Отношение сжатия
Австралия.hcl
500 x 395
771
36
21:1
Алтай.hcl
430 x 409
687
78
9:1
Африка.hcl
700 x 730
1460
60
24:1
Несжимаемый.hcl
200 x 200
117
156
1:1,3
тест выравнивания.hcl
400 x 200
312
10
31:1
Южная Америка.hcl
735 x 1125
3150
107
29:1
Из проведенного исследования можно создать последующие выводы:
· применение способа группового кодировки в данной работе стопроцентно оправдано, так как при использовании его в отношении карт изообластей высот, наблюдаются довольно высочайшие характеристики сжатия (от 9:1 до 29:1, карта «Тест выравнивания» не учитывается, потому что она не является настоящей картой). Единственным недочетом использования этого способа является незначимое повышение времени загрузки кодированных файлов в программку «Редактор карт» (это не демонстрировалось в данном исследовании);
· единственный вариант, когда размер кодированного файла превосходит размер начального файла, наблюдается на особом примере, призванном показать недочет способа.
5. Заключение
Разработанный программный комплекс отвечает всем предъявляемым к нему требованиям. Он обеспечивает возможность сотворения карт изообластей («Редактор карт») и построения в настоящем времени на их базе трехмерных изображений ландшафтов («Просмотр ландшафта»). В нем реализованы все рассмотренные в данной работе методы машинной графики. Проведены исследования работы алгоритмов на разных наборах начальных данных. Тем не наименее, существует огромное количество путей усовершенствования описанного программного комплекса.
Во-1-х, построение ландшафта может быть лишь на базе верно размеченной карты изообластей высот – нереально внедрение, к примеру, файла, приобретенного в итоге сканирования некой карты. Но подготовка (разметка) карты изообластей вручную – весьма трудозатратный процесс. Автоматизация процесса разметки существенно расширила бы способности программного комплекса.
Во-2-х, получаемые изображения трехмерных ландшафтов смотрятся не близко к реальности – они только разрешают получить инфы о географических объектах, присутствующих в области, представляемой ландшафтом. Добавление способности текстурирования и подписи географических объектов повысили бы информативность получаемого изображения ландшафта.
Но, описанные трудности весьма сложны (определение и разметка карт), а некие из их выходят за рамки машинной графики.
6. Перечень литературы
1. Роджерс Д. Алгоритмические базы машинной графики: пер. с англ.— М.: мир, 1989.— 512 с.: ил.
2. Порев В. Н. Компьютерная графика. – СПб.: БХВ-Петербург, 2002. – 432 с.: ил.
3. Никулин Е. А. Компьютерная геометрия и методы машинной графики. СПб.: БХВ-Петербург, 2003. – 560с.: ил.
4. Авдеева С.М., Куров А.В. методы трехмерной машинной графики: Учебное пособие. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1996. – 60 с.: ил.
5. Архангельский А.Я. Приемы программирования в Delphi. – М.: ООО «Двучлен-Пресс», 2003. – 784 с.: ил.
6. HTTP://www.xdev.ru – «Генерация трехмерных ландшафтов».
Оглавление
1. Введение. 1
2. Конструкторская часть. 2
2.1. Выбор, обоснование и описание применяемых алгоритмов и понятий машинной графики. 2
2.1.1. Равномерная сетка высот. 2
2.1.2. Выравнивание ландшафта. 4
2.1.3. Трехмерные аффинные преобразования. 5
2.1.4. Проецирование. 6
2.1.5. Отображение в окне. 7
2.1.6. метод Z-буфера. 8
2.1.7. Освещение. 10
2.1.7.1. Однотонная закраска (способ гранения) 11
2.1.7.2. Способ Гуро. 11
2.1.7.3. Способ Фонга. 13
2.1.7.4. анализ способов Гуро и Фонга. 14
2.1.8. Последовательность действий при визуализации сцены.. 15
2.2. Типы, структуры данных и функции,
использованные при реализации программного комплекса. 16
2.2.1. структура файла для хранения карт изообластей. 18
2.2.2.4. Распределение программки по модулям. 19
2.2.2.5. Связи меж модулями программки.. 20
2.2.3. программка «Просмотр ландшафта». 21
2.2.3.1. Процедуры манипуляции изображением ландшафта. 21
2.2.3.2. Z-буфер. 22
2.2.3.3. Буфер кадра. 22
2.2.3.4. Процедуры визуализации ландшафта. 22
2.2.3.2. Тип и структура файла для хранения ландшафта. 23
2.2.3.3. Распределение программки по модулям. 24
2.2.3.4. Связи меж модулями программки.. 25
3. Технологическая часть. 26
3.1. Выбор языка программирования. 26
3.2. Описание программного комплекса. 26
3.2.1. программка «Редактор карт». 26
3.2.1.1. Общие сведения. 26
3.2.1.2. интерфейс программки.. 27
3.2.1.3. Работа программки.. 29
3.2.2. программка «Просмотр ландшафта». 30
3.2.2.1. Общие сведения. 30
3.2.2.2. интерфейс программки.. 30
3.2.2.3. Работа программки.. 33
3.2.3. Системные требования. 34
4. Экспериментально-исследовательская часть…. 35
4.1. Исследование № 1. 36
4.2. Исследование № 2. 38
4.3. Исследование № 3. 40
5. Заключение. 41
6. Перечень литературы.. 42
]]>