Учебная работа. Курсовая работа: Математические модели в расчетах на ЭВМ

Учебная работа. Курсовая работа: Математические модели в расчетах на ЭВМ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНБАССКИЙ ГОСУДАРСТВЕННЫЙ технический УНИВЕРСИТЕТ

Кафедра АУТПТЭК

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе

по дисциплине:

«Математические модели в расчетах наЭВМ»

Выполнил:

студент гр.АКГ-05

Коновалов А.А.

Проверил:

ст.преп. Склярова Г.А

асс. Марусей О.В.

Алчевск 2007

РЕФЕРАТ

Данная курсовая работа содержит 30 страничек, 16 рисунков, 2 таблицы, 3 источника литературы.

Целью данной курсовой работы является построение АЧХ, КЧХ, ФЧХ (моделирование в частотной области) и переходный процесс (моделирование во временной области).

В итоге выполненной курсовой работы были получены ФЧХ, КЧХ, ФЧХ и переходный процесс.

СТРУКТУРНАЯ СХЕМА, ПЕРЕДАТОЧНАЯ ФУНКЦИЯ, МАТЕМАТИЧЕСКАЯ МОДЕЛЬ, ЧАСТОТНЫЕ свойства, КРИВАЯ ПЕРЕХОДНОГО ПРОЦЕССА.

СОДЕРЖАНИЕ

Введение

1. Моделирование в частотной области

2. Моделирование во временной области

Заключение

Список ссылок

ВВЕДЕНИЕ

Нередко при решении задач автоматизации приходится прибегать к моделированию. Это связанно с тем, что большая часть технологических объектов являются сложными и изучить реакцию этих объектов на те либо другие объекты является довольно дорогой операцией.

Различают три главных вида модели:

— алгоритмическая

— физическая

— математическая

Алгоритмическая модель — это некая последовательность действий и операций.

Физическая модель — это четкая копия технологического объекта в увеличенном либо уменьшенном масштабе.

Математическая модель быть может представлена в виде алгебраических либо систем алгебраических, дифференциальных либо систем дифференциальных уравнений.

В виду удобства работы наибольшее распространение при исследовании получили математические модели.

В данной работе произведем моделирование соединения звеньев в частотной области.

1 МОДЕЛИРОВАНИЕ В ЧАСТОТНОЙ ОБЛАСТИ

Все технологические объекты являются довольно сложными объектами и они описываются дифференциальными уравнениями больших порядков либо системой дифференциальных уравнений. Для исследования объекта в частотной области довольно выстроить надлежащие частотные свойства:

— амплитудно-частотная черта указывает зависимость амплитуды сигнала на выходе объекта от частоты сигнала на его входе при постоянной амплитуде входного сигнала;

— фазочастотная черта указывает на сколько (на какой угол) выходной сигнал опережает либо отстает от входного сигнала при изменении частоты входного сигнала от 0 до ∞;

— всеохватывающая частотная черта либо амплитудно-фазная черта указывает, как меняется в всеохватывающей плоскости модуль и фаза исследуемого объекта при изменении частоты от 0 до ∞.

Проводим моделирование в частотной области соединения звеньев представленных в задании на рисунке 1.1

При узнаваемых передаточных функциях:

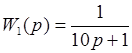
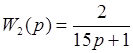
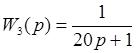
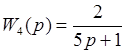
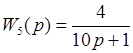
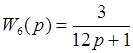
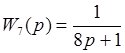
Введем формулы для вычисления частотных функций, амплитуды и фазы данных звеньев:

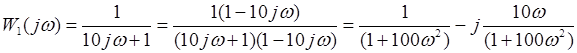
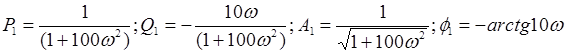
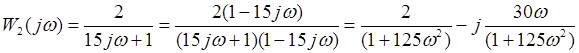
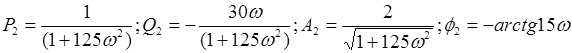
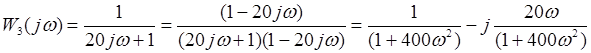
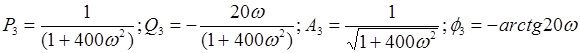
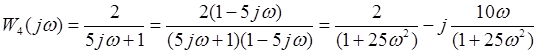
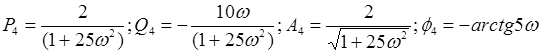
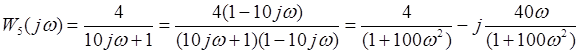
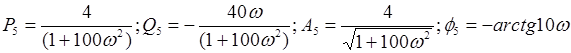
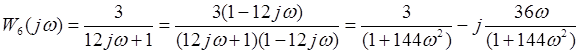
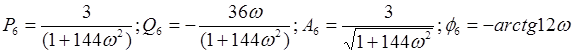
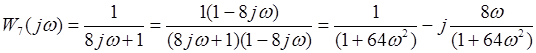
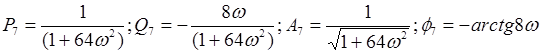
Выполним преобразования структурной схемы. При преобразовании структурных звеньев нужно будет отыскивать значения передаточной и частотой (производим подмену p=jω) функций, общей вещественной и общей надуманной составляющих, модуля и фазы приобретенных звеньев.

Для параллельного соединения эти значения рассчитываются по формулам (1.1)-(1.6):

(1.1)

где — передаточная функция i-того звена.

(1.2)

где (jω) — частотная функция i-того звена.

(1.3)

где — вещественная составляющая i-того звена.

(1.4)

где — надуманная составляющая i-того звена.

(1.5)

. (1.6)

При поочередном соединении значения будут рассчитываться по формулам (1.7)-(1.12):

(1.7)

где — передаточная функция i-того звена.

(1.8)

где (jω) — частотная функция i-того звена.

(1.9)

где — модуль i- того звена.

(1.10)

где — фаза i- того звена.

(1.11)

(1.12)

Выполним эквивалентные преобразования данных соединений частей. Заменим параллельное соединение звеньев , одним эквивалентным звеном (набросок 1.2).

Y

Набросок 1.2 – Структурные преобразования

При параллельном соединении звеньев передаточная и частотная функции находятся по формулам (1.1)-(1.2):

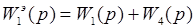
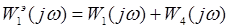
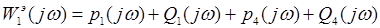
Общая вещественная составляющая и общая надуманная составляющая определяются соответственно как сумма вещественных и сумма надуманных составляющих отдельных звеньев по формулам (1.3)-(1.4):

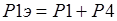
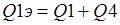
При параллельном соединении удобнее работать с вещественными и надуманными составляющими. Если требуется вычислить модуль и фазу такового соединения, то результирующие модуль и фаза определяются по формулам

(1.5)-(1.6):

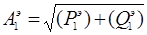
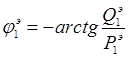
Заменим параллельное соединение звеньев одним эквивалентным звеном (набросок 1.3).

W7(P)

W6(P)

W3(P)

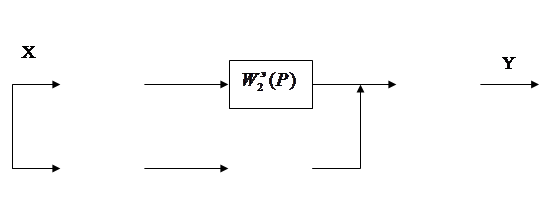
Набросок 1.3 – Структурные преобразования

При параллельном соединении звеньев передаточная и частотная функции находятся по формулам (1.1)-(1.2):

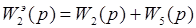
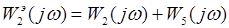
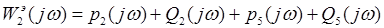
Общая вещественная составляющая и общая надуманная составляющая определяются соответственно как сумма вещественных и сумма надуманных составляющих отдельных звеньев по формулам (1.3)-(1.4):

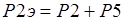
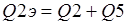
При параллельном соединении удобнее работать с вещественными и надуманными составляющими. Если требуется вычислить модуль и фазу такового соединения, то результирующие модуль и фаза определяются по формулам (1.5)-(1.6):

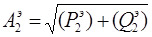
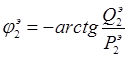
Заменим последовательное соединение звеньев , одним

эквивалентным звеном (набросок 1.4).

W3(P)

W(P)

XY

Набросок 1.4 — Структурные преобразования

При поочередном соединении удобнее работать с модулями и фазами звеньев. Определим их по формулам (1.9)-(1.10):

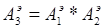
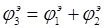
По формулам (1.11)-(1.12) определим общую вещественную и общую надуманную составляющие:

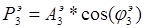
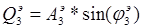
Заменим последовательное соединение звеньев , одним эквивалентным звеном (набросок 1.5).

W(P)

W3(P)

XY

Набросок 1.5 — Структурные преобразования

При поочередном соединении удобнее работать с модулями и фазами звеньев. Определим их по формулам (1.9)-(1.10):

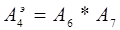
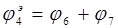
По формулам (1.11)-(1.12) определим общую вещественную и общую надуманную составляющие:

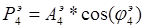
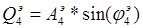
Заменим параллельное соединение звеньев , одним эквивалентным звеном (набросок 1.6).

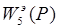
W3(P)

XY

Набросок 1.6 — Структурные преобразования

При параллельном соединении звеньев передаточная и частотная функции находятся по формулам (1.1)-(1.2):

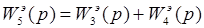
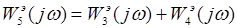
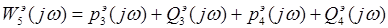
Общая вещественная составляющая и общая надуманная составляющая определяются соответственно как сумма вещественных и сумма надуманных составляющих отдельных звеньев по формулам (1.3)-(1.4):

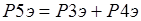
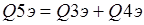
При параллельном соединении удобнее работать с вещественными и надуманными составляющими. Если требуется вычислить модуль и фазу такового соединения, то результирующие модуль и фаза определяются по формулам (1.5)-(1.6):

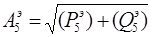
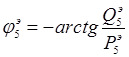
Заменим последовательное соединение звеньев , одним эквивалентным звеном (набросок 1.7).

W(P)

XY

Набросок 1.7 — Структурные преобразования

При поочередном соединении удобнее работать с модулями и фазами звеньев. Определим их по формулам (1.9)-(1.10):

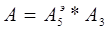
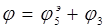
По формулам (1.11)-(1.12) определим общую вещественную и общую надуманную составляющие:

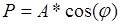
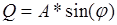
1





Блок-схема метода представлена на рисунке 1.8

нет





10

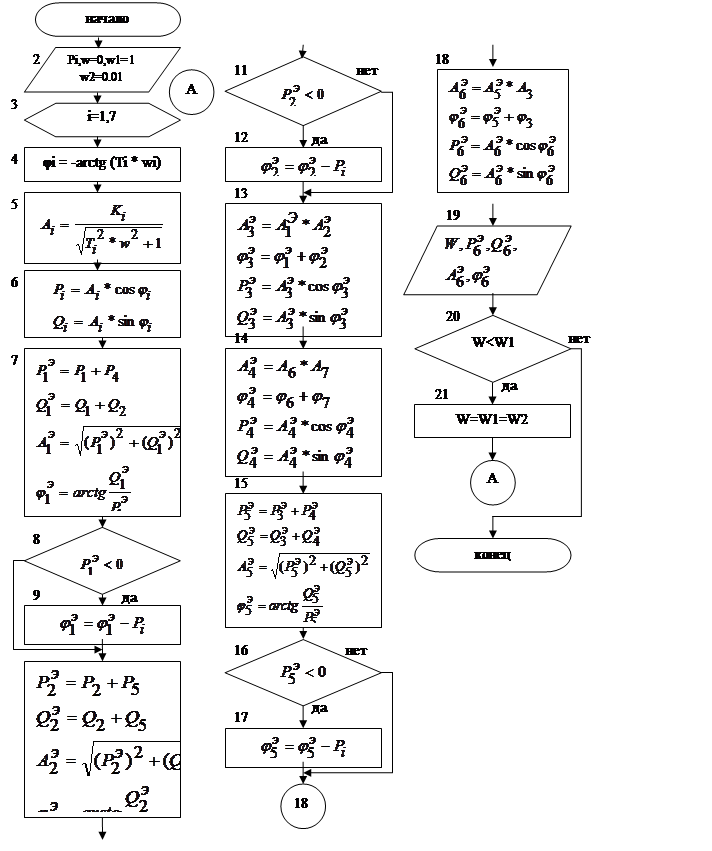
Набросок 1.8 – Блок – схема метода решения задачки

текст разработанной программки приведён на рисунке 1.9.

При разработке были введены последующие идентификаторы:

W- изначальное значения частоты;

W1- конечное значение частоты;

W2- шаг конфигурации частоты.

Для ввода значений характеристик звеньев и употребляются массивы К(7) и Т(7). Ввод значений этих характеристик осуществляется при помощи операторов DATAREAD. Вычисленные значения выходных переменных сохраняются в файле mm_8 txt на диске А.

OPEN «A:mm_8.txt» FOR OUTPUT AS #2

CLS : Pi = 3.141592654#: W = 0: W1 = 1: W2 = .05

DIM K(7), T(7)

DATA 1,10,2,15,1,20,2,5,4,10,3,12,1,8

FOR i = 1 TO 7

READ K(i), T(i)

PRINT USING «K(#)=#, T(#)=##»; i; K(i); i; T(i)

NEXT i

10 FOR i = 1 TO 7

A(i) = K(i) / SQR(T(i) ^ 2 * W ^ 2 + 1)

F(i) = -ATN(T(i) * W)

P(i) = A(i) * COS(F(i))

Q(i) = A(i) * SIN(F(i))

NEXT i

REM ПАРАЛЛЕЛЬНОЕ соединение

Pe(1) = P(1) + P(4)

Qe(1) = Q(1) + Q(4)

Ae(1) = SQR(Pe(1) ^ 2 + Qe(1) ^ 2)

Fe(1) = ATN(Qe(1) / Pe(1))

IF Pe(1) < 0 THEN Fe(1) = Fe(1) – Pi

REM ПАРАЛЛЕЛЬНОЕ соединение

Pe(2) = P(2) + P(5)

Qe(2) = Q(2) + Q(5)

Ae(2) = SQR(Pe(2) ^ 2 + Qe(2) ^ 2)

Fe(2) = ATN(Qe(2) / Pe(2))

Набросок 1.9, лист1- Листинг программки.

IF Pe(2) < 0 THEN Fe(2) = Fe(2) – Pi

REM ПОСЛЕДОВАТЕЛЬНОЕ соединение

Ae(3) = Ae(1) * Ae(2)

Fe(3) = Fe(1) + Fe(2)

Pe(3) = Ae(3) * COS(Fe(3))

Qe(3) = Ae(3) * SIN(Fe(3))

REM ПОСЛЕДОВАТЕЛЬНОЕ соединение

Ae(4) = A(6) * A(7)

Fe(4) = F(6) + F(7)

Pe(4) = Ae(4) * COS(Fe(4))

Qe(4) = Ae(4) * SIN(Fe(4))

REM ПАРАЛЛЕЛЬНОЕ соединение

Pe(5) = Pe(3) + Pe(4)

Qe(5) = Qe(3) + Qe(4)

Ae(5) = SQR(Pe(5) ^ 2 + Qe(5) ^ 2)

Fe(5) = ATN(Qe(5) / Pe(5))

IF Pe(5) < 0 THEN Fe(5) = Fe(5) — Pi

REM ПОСЛЕДОВАТЕЛЬНОЕ соединение

Ae(6) = Ae(5) * A(3)

Fe(6) = Fe(5) + F(3)

Pe(6) = Ae(6) * COS(Fe(6))

Qe(6) = Ae(6) * SIN(Fe(6))

PRINT USING «W=#.##, Ae(#)=+##.###, Fe(#)=+#.###, Pe(#)=+##.###, Qe(#)=+#.###»; W; 6; Ae(6); 6; Fe(6); 6; Pe(6); 6; Qe(6)

PRINT #2, USING «#.## +##.### +#.### +##.### +##.###»; W; Ae(6); Fe(6); Pe(6); Qe(6)

REM ПРОВЕРКА ДИАПАЗОНА ЧАСТОТЫ

IF W < W1 THEN W = W + W2

IF W < W1 THEN GOTO 10

CLOSE #2

END

Набросок 1.9, лист 2- Листинг программки моделирования в частотной области

Приобретенные результаты занесём в таблицу 1.1

Таблица 1.1 – Результаты расчетов

ω
Ae(6)
Fe(6)
Pe(6)
Qe(6)

0.00
+21.000
+0.000
+21.000
+0.000

0.05
+11.973
-1.631
-0.718
-11.951

0.10
+4.996
-2.523
-4.071
-2.896

0.15
+2.328
-3.030
-2.313
-0.258

0.20
+1.227
-3.354
-1.199
+0.259

0.25
+0.712
-3.578
-0.646
+0.301

0.30
+0.446
3.741
-0.368
+0.251

0.35
+0.295
-3.864
-0.221
+0.195

0.40
+0.205
-3.961
-0.140
+0.150

0.45
+0.147
-4.038
-0.092
+0.115

0.50
+0.110
-4.102
-0.063
+0.090

0.55
+0.083
-4.154
-0.044
+0.071

0.60
+0.065
-4.199
-0.032
+0.057

0.65
+0.052
-4.237
-0.024
+0.046

0.70
+0.042
-4.270
-0.018
+0.038

0.75
+0.034
-4.298
-0.014
+0.031

0.80
+0.028
-4.324
-0.011
+0.026

0.85
+0.024
-4.346
-0.008
+0.022

0.90
+0.020
-4.366
-0.007
+0.019

0.95
+0.017
-4.384
-0.005
+0.016

По приобретенным данным построим графики, рис. 1.9 – 1.11

Набросок 1.10 – Всеохватывающая частотная черта соединения звеньев

Набросок 1.11 – Амплитудно-частотная черта соединения звеньев

Набросок 1.12 — Фазо-частотная черта соединения звеньев

2 МОДЕЛИРОВАНИЕ ВО ВРЕМЕННОЙ области

Провести моделирование во временной области соединения звеньев представленных на рисунке 2.1.

y3





y2





y1

W2(P)

W3(P)

W1(P)

Набросок 2.1 – Схема соединения звеньев

Передаточные функции частей имеют вид:

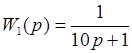
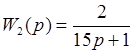
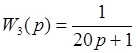
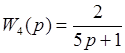
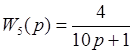
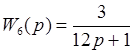
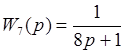
До этого чем перейти к моделированию во временной области нужно составить в согласовании с данной структурой соединения частей, систему дифференциальных уравнений, которой будет описываться данная система. При всем этом следует держать в голове, что все численные способы дают более четкое решение для дифференциальных уравнений первого порядка.

Передаточной функцией именуется отношение изображения по Лапласу выходной величины, к изображению по Лапласу входной величине при нулевых исходных критериях, формула (2.1):

(2.1)

Составим систему дифференциальных уравнений в согласовании с (2.1):

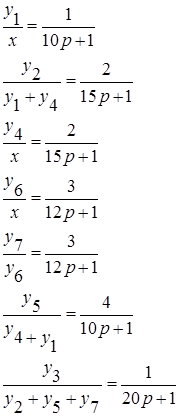
Преобразуем приобретенные формулы:

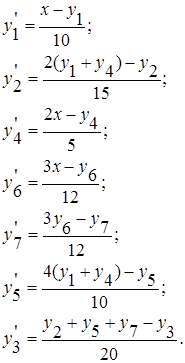
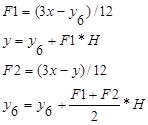
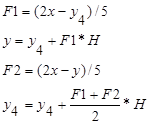
Блок-схема метода представлена на рисунке 2.2





1

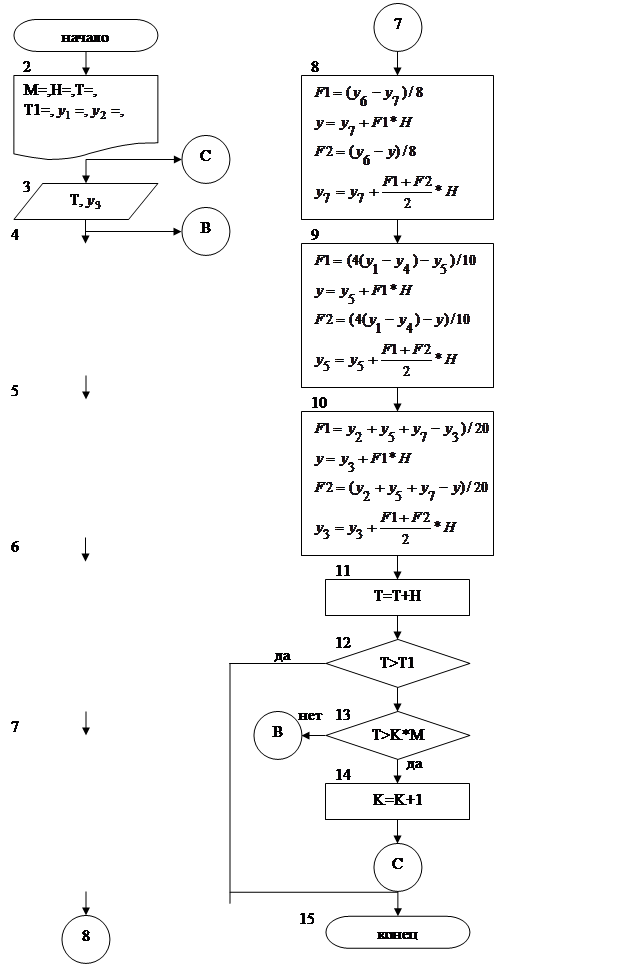
текст разработанной программки приведён на рисунке 2.3. При разработке программки были введены последующие идентификаторы:

T – изначальное

T1 – конечное

H – шаг интегрирования,

М – шаг печати,

К – для организации печати с принятым шагом.

Для вычисления правых частей уравнения системы введены идентификаторы F1-F2. Текущее значение интегральной кривой, являющейся выходной функцией, хранящееся в переменной Y3.

CLS

PRINT «Моделирование во временной области«

PRINT «Введите M, H, T, T1»

INPUT M, H, T, T1

YI = 0: Y2 = 0: Y3 = 0: Y4 = 0: Y5 = 0: Y6 = 0: Y7 = 0: K = 1: X = 1

15 PRINT «T=»; T, «Y3=»; Y3

20 F1 = (X — Y1) / 10: Y = Y1 + F1 * H

F2 = (X — Y) / 10: Y1 = Y1 + ((F1 + F2) / 2) * H

F1 = (2 * (Y1 + Y4) — Y2) / 15: Y = Y2 + F1 * H

F2 = (2 * (Y1 + Y4) — Y) / 15: Y2 = Y2 + ((F1 + F2) / 2) * H

F1 = (2 * X — Y4) / 5: Y = Y4 + F1 * H

F2 = (2 * X — Y) / 5: Y4 = Y4 + ((F1 + F2) / 2) * H

F1 = (3 * X — Y6) / 12: Y = Y6 + F1 * H

F2 = (3 * X — Y) / 12: Y6 = Y6 + ((F1 + F2) / 2) * H

F1 = (Y6 — Y7) / 8: Y = Y7 + F1 * H

F2 = (Y6 — Y) / 8: Y7 = Y7 + ((F1 + F2) / 2) * H

F1 = (4 * (Y1 + Y4) — Y5) / 10: Y = Y5 + F1 * H

F2 = (4 * (Y1 + Y4) — Y) / 10: Y5 = Y5 + ((F1 + F2) / 2) * H

F1 = (Y2 + Y5 + Y7 — Y3) / 20: Y = Y3 + F1 * H

F2 = (Y2 + Y5 + Y7 — Y) / 20: Y3 = Y3 + ((F1 + F2) / 2) * H

T = T + H

IF T > T1 THEN 100

IF T >= K * M THEN 80 ELSE 85

80 K = K + 1: GOTO 15

85 GOTO 20

CLS

100 END

Набросок 2.3 – Листинг программки моделирования во временной области

Опосля пуска программки были получены значения T и Y приведенные в таблице 2.1.

Таблица 2.1 – Значения T и Y

T
Y

0
0

20.00036
4.917364

40.00929
12.89664

60.00594
17.53008

80.00868
19.61416

100.003
20.46468

120.0072
20.79692

140.0023
20.92336

160.0013
20.97077

180.0004
20.98832

200.0094
20.99452

220.0084
20.99666

240.0074
20.99666

260.0025
20.99666

280.002
20.99666

300.0015
20.99666

По значениям, взятым из таблицы 2.1 построим переходную функцию соединения, приведенную на рисунке 2.4.

Набросок 2.4 – График переходной функции данной системы.

ЗАКЛЮЧЕНИЕ

В данной работе мы разглядели моделирование в частотной и во временной областях. По приобретенным данным выстроили Амплитудно-фазную характеристику, амплитудно-частотную характеристику, фазо-частотную характеристику (моделирование в частотной области) и переходный процесс (моделирование во временной области). Программное обеспечение было создано на алгоритмическом языке Microsoft QuickBASIC. При построении графиков был применен пакет Mathcad 11 Enterprise Edition.

ПЕРЕЧЕРЬ ССЫЛОК

1. Бесерский В.А., Попов Е.П., Теория систем автоматического регулирования. – М.: Наука, 1972. – 798 с.

]]>