(5 оценок, среднее: 4,80 из 5)
Загрузка...
Учебная работа. Доклад: Дедукция
дедукция (от лат. deductio-выведение) в широком смысле представляет собой форму мышления, состоящую в том, что новое предложение (а поточнее, выраженная в нем идея) выводится чисто логическим методом, т. е. по определенным правилам логического вывода (следования) из неких узнаваемых предложений (мыслей).
В первый раз теория дедукции (логического вывода) была разработана Аристотелем. Эта теория развивалась, совершенствовалась с развитием науки логики. Особенное развитие с учетом потребностей арифметики она получила в виде теории подтверждения в математической логике.
Дедуктивное рассуждение (умозаключение) различается от индуктивного либо рассуждения по аналогии достоверностью заключения, т. е. в дедуктивном рассуждении заключение поистине, по последней мере когда истинны все посылки. В отличие от индукции (неполной) и аналогии в дедуктивном рассуждении недозволено получить неверное заключение из настоящих посылок. Конкретно потому дедуктивные рассуждения употребляются в математических подтверждениях (подтверждениях математических предложений).
Обширное применение дедукции в арифметике обосновано аксиоматическим способом построения математических теорий.
Аксиоматический способ по существу представляет собой типичный способ установления истинности предложений математической теории, состоящий в последующем: некие предложения, выражающие главные характеристики начальных понятий либо дела меж ними, принимаются за настоящие. Это начальные предложения, либо теоремы теории. Истинность же других предложений, теорем данной нам теории, устанавливается при помощи дедуктивных доказательств, т. е. все другие предложения теории логически выводятся (дедуцируются) из предыдущих им предложений, т. е. из аксиом, определений и ранее доказанных теорем. Вот почему арифметику и именуют «дедуктивной» наукой (в ней все выводится, «дедуцируется» из неких начальных фактов, выраженных в теоремах).
дедукция как способ обучения арифметике включает:
1) обучение (педагогический процесс, в результате которого учащиеся под руководством учителя овладевают знаниями, умениями и навыками) дедуктивным доказательствам и
2) обучение (педагогический процесс, в результате которого учащиеся под руководством учителя овладевают знаниями, умениями и навыками) расширению дедуктивной системы включением в нее новейших предложений, т. е. преобразованию совокупы предложений, приобретенных опытным методом, либо при помощи индукции, аналогии либо остальных эвристических способов, в систему предложений, упорядоченных отношением следования, расширяющую уже изученный фрагмент теории.
Разглядим эти два нюанса дедукции как способа обучения.
1) Под обучением подтверждению мы осознаем обучение (педагогический процесс, в результате которого учащиеся под руководством учителя овладевают знаниями, умениями и навыками) мыслительным действиям поиска и построения подтверждения, а не проигрыванию и заучиванию готовых доказательств. В таком осознании это педагогическая задачка главного общеобразовательного и воспитательного значения, выходящего за рамки математического образования. Учить обосновывать значит до этого всего учить рассуждать, а это одна из главных задач обучения совершенно. Что все-таки касается значимости данной нам задачки для усвоения математических познаний, то она соразмерна значимости подтверждения в самой арифметике.
Поиск доказательств осуществляется средствами, хорошими от дедуктивных, и вопросец о обучении поиску подтверждения будет предметом последующего параграфа.
Обучение (педагогический процесс, в результате которого учащиеся под руководством учителя овладевают знаниями, умениями и навыками) поиску и построению доказательств направляется 3-мя главными вопросцами: «Что?», «Откуда?», «Как?»
а) Что? — что доказывается? Каково «доказываемое» предложение, для которого мы отыскиваем подтверждение? Как оно формулируется? Все ли понятно в данной нам формулировке? недозволено ли по другому формулировать доказываемое предложение? Что «дано»? Что «требуется обосновать»? Это далековато не полный список вопросцев, которые мы объединяем в одном вопросце «Что?». Они соединены с исследованием доказываемого предложения, с вероятным приведением его к наиболее комфортному для выяснения критерий и заключения виду. К примеру, представление доказываемых предложений в виде импликаций с внедрением связки «если…, то…» упрощает учащимся выявление того, что «дано» (предложение, записанное меж словами «если» и «то») и что «требуется обосновать» (предложение, записанное опосля слова «то»). К примеру, расчленение аксиомы «Вертикальные углы равны» на условие и заключение обычно -вызывает затруднения у учащихся, но эти затруднения сходу устраняются, если сконструировать аксиому в виде импликации: «Если углы вертикальные, то они равны». Аналогично аксиома «Диагонали ромба взаимно перпендикулярны» представляется в форме «Если параллелограмм — ромб, то его диагонали взаимно перпендикулярны», в какой просто найти условие и заключение.
нужно выяснять все условия аксиомы. Так, мы не сможем обосновать, что среднее арифметическое 2-ух чисел больше их среднего геометрического, если не учтем, что это правильно только для 2-ух положительных и неравных меж собой чисел. Это подчеркивается в последующей записи данной нам аксиомы в виде импликации: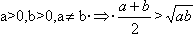 
б) Откуда? — откуда, из каких посылок следует (может следовать) доказываемое предложение? Из каких уже узнаваемых настоящих предложений данной области (аксиом, определений, ранее доказанных теорем) можно было бы «вывести» это предложение?
Ответ на этот вопросец просит концентрации внимания на содержании критерий и заключения доказываемого предложения с целью выделения тех уже узнаваемых предложений, которые как-то соединены с этими критериями. совокупа этих предложений составляет базу для поиска подтверждения. Эти совокупы могут быть разными, указывая на разные направления поиска, приводящие к разным доказательствам одной и той же аксиомы. К примеру, готовясь к подтверждению аксиомы о 3-х .перпендикулярах, мы можем выделить (вспомянуть) совокупа узнаваемых предложений, связанных с перпендикулярностью прямой и плоскости (определение, признак), но можем также мыслить о предложениях, связанных с перпендикулярностью векторов. В итоге мы получаем два направления поиска и два разных подтверждения аксиомы о 3-х перпендикулярах.
в) Как? — как доказываемое предложение выходит (выводится) из ранее узнаваемых предложений (аксиом, определений, теорем)?
Этот вопросец находит в массовой практике обучения обычной ответ: «При помощи рассуждения». Так разъясняется понятие подтверждения в сейчас работающих и пробных учебных пособиях по геометрии для VI-Х классов школы. Сиим объяснением интуитивное понятие подтверждения сводится к другому интуитивному же понятию рассуждения, которое, по-видимому, считается наиболее ясным. Но навряд ли слово «рассуждение» гласит учащимся намного больше, чем слово «подтверждение», не говоря уже о том, что не всякое рассуждение может служить подтверждением (имеет доказательную силу).
Можно полагать (и некие опыты подтверждают), что по вопросцу о том, как мы рассуждаем, можно подняться в школьном обучении (по последней мере в школах с углубленным исследованием арифметики либо на факультативных упражнениях) на наиболее высочайший уровень, можно достигнуть некого прогресса в осознании того, что такое подтверждение, в уточнении этого понятия.
Выделим в обучении подтверждению два главных уровня. На первом уровне (IV-VII классы) применяемые в подтверждениях (неявно) логические средства вывода не выявляются, не разъясняются, основное внимание уделяется выяснению того, «что доказывается» и «из что это следует», но не «как это следует». На этом уровне подтверждение рассматривается совершенно как рассуждение, при помощи которого истинность 1-го (доказываемого) предложения устанавливается на базе истинности остальных предложений.
На втором уровне (в старших классах, на факультативных упражнениях либо в школах с углубленным исследованием арифметики) учащимся могут быть разъяснены простые правила вывода и на данной нам базе уточнено понятие подтверждения. Это уточнение достигается при помощи представления подтверждения в определенной, обычной форме, поддающейся четкому описанию. На этом уровне учащимся становится легкодоступным анализ подтверждения, выявление его логической структуры, применяемых в нем правил вывода, запись содержательного подтверждения в полной логической форме, т. е. его формализация.
Очевидно, в практике обучения постоянно применялись и будут применяться содержательные подтверждения, выставленные в виде обыденных рассуждений и уровень строгости которых адекватен способностям учащихся. Этот уровень должен естественным образом повышаться от класса к последующему в согласовании с развитием этих способностей (а не напротив, как это наблюдается в неких учебных пособиях, в каких уровень строгости доказательств в VI классе выше, чем в IX).
В практике обучения учитель, как правило, сам обосновывает в классе каждую подлежащую исследованию аксиому (а то и два раза либо даже три раза повторяет ее). Таковой способ нацелен основным образом на доказательств определенных теорем, и навряд ли можно таковым способом обучить учащихся обосновывать. Сочетая же этот способ с способом обучения поиску подтверждения, мы научим их обосновывать. Сам же поиск подтверждения, как и всякий поиск, просит творческого мышления и развивает его. Потому способ обучения поиску подтверждения увеличивает воздействие обучения на интеллектуальное развитие учащихся, на развитие их творческого мышления.
2) В процессе обучения (опытным методом либо при помощи эвристических способов) открываем, что при условии А имеет пространство некое свойство В. В таком случае предстоит обосновать аксиому, имеющую вид импликации А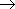
В, где А — условие, а В — заключение аксиомы.
Опосля подтверждения аксиомы А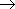 В изученный фрагмент теории, к примеру геометрии, расширяется, включая и это предложение, которое в предстоящем уже может употребляться в качестве одной из посылок при подтверждении остальных, новейших теорем.
Но расширено фрагмента теории лишь одним предложением, свойственное для установившейся методики обучения, не является более оптимальным методом продвижения в теорию, расширения познаний применением дедукции в качестве способа обучения. Во-1-х, этот метод не отражает специфичности способа дедукции в самой арифметике. При описании настоящих ситуаций, как правило, получают не одно предложение, а совокупа предложений, которая потом исследуется с целью логического упорядочения, перевоплощения в «небольшую» теорию, присоединяемую к уже изученному (построенному) фрагменту «большенный» теории. Во-2-х, обыденное внедрение дедукции в обучении нерационально, малоэффективно и с дидактической точки зрения. Выдвигаемый в методической литературе тезис обучения «укрупненными блоками» применительно к дедуктивно построенному фрагменту учебного материала по существу значит продвижение в теорию не единичными предложениями, а малеханькими теориями, описывающими определенные ситуации, фигуры и т. п.
]]>