Учебная работа. Доклад: Применение теоремы Эйлера к некоторым задачам
В данной нам статье мы хотим предложить читателям несколько задач, в решении которых центральную роль играет аксиома Эйлера. Уделяя основное внимание задачкам, мы не доказываем тут эту аксиому, а приводим только её формулировку. подтверждение аксиомы Эйлера, как и наиболее общие формулировки данной нам аксиомы, можно отыскать в книжках «Что такое математика?» Куранта и Роббинса и «Приятная геометрия» Гильберта и Кон-Фоссена.
До этого чем формулировать аксиому Эйлера, договоримся, что линию с концами в 2-ух данных точках мы будем именовать дугой, соединяющей эти точки, в том случае, если эту линию можно пройти, не побывав ни в одной из её точек два раза.
Аксиома Эйлера. Пусть на плоскости задано m точек и n попарно непересекающихся дуг, любая из которых соединяет какие-либо две данные точки и не проходит через другие m–2 точки, и пусть эти дуги делят плоскость на l областей. Если из каждой данной точки в всякую из других можно попасть, двигаясь по сиим дугам, то
m – n + l = 2.
В случае, изображенном на рисунке1, все условия аксиомы Эйлера выполнены, m=12, n=18, l=8 и m–n+l=2. На рисунках2 и 3 изображены случаи, когда условия данной нам аксиомы не производятся. Так, на рисунке2 из точки A1
недозволено попасть в точку A5
и m–n+l=3≠2, а на рисунке3 линия, соединяющая точки A1
и A2
, является самопересекающейся и снова m–n+l=3≠2.
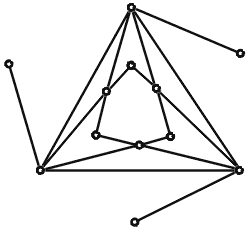
Рис. 1.
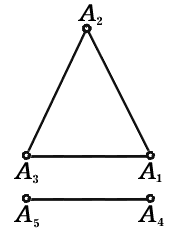
Рис. 2.
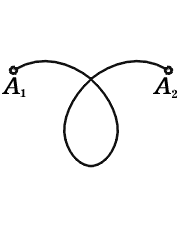
Рис. 3.
В неких задачках совокупа, состоящую из нескольких точек и соединяющих их попарно непересекающихся дуг, мы называем картой; при всем этом точки из данной нам совокупы мы называем верхушками, а области, на которые дуги делят плоскость, — странами.
сейчас мы можем перейти к решению задач.
задачка1. Можно ли 10 городов соединить меж собой непересекающимися дорогами так, чтоб из всякого городка выходило 5 дорог, ведущих в 5 остальных городов?
Решение. Представим, что городка можно соединить меж собой дорогами так, как обозначено в задачке. В таком случае, если какие-то два городка окажутся не соединенными дорогой конкретно, то найдётся 3-ий город, который уже будет конкретно соединён с каждым из их. Изобразив на плоскости городка точками, а дороги — дугами, получим, что любые две точки соединены цепочкой дуг. Потому что в каждой точке сходятся 5 дуг, то общее число дуг равно ½·5·10 = 25. Согласно аксиоме Эйлера эти дуги делят плоскость на 2 + 25 – 10 = 17 областей. Любая из этих семнадцати областей ограничена по последней мере 3-мя дугами, потому что в неприятном случае нашлись бы два городка, конкретно соединённые по последней мере 2-мя дорогами, а это противоречит условию задачки. Как следует, число дуг не меньше ½·3·17 = 25,5. Таковым образом, начальное предположение приводит нас к противоречию, и городка недозволено соединить меж собой так, как это требуется в задачке.
задачка2. Три поссорившихся соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от всякого дома к любому колодцу?
Решение. Представим, что это создать можно.
Изобразим дома голубыми, а колодцы — чёрными точками и каждую голубую точку соединим дугой с каждой чёрной точкой так, чтоб девять приобретенных дуг попарно не пересекались. Тогда всякие две точки, изображающие дома либо колодцы, будут соединены цепочкой дуг, и в силу аксиомы Эйлера эти девять дуг поделят плоскость на 9–6+2=5 областей. Любая из 5 областей ограничена по последней мере 4-мя дугами, потому что по условию задачки ни одна из дорожек не обязана конкретно соединять два дома либо два колодца. Потому число дуг обязано быть не меньше ½·5·4 = 10, и, как следует, наше предположение ошибочно.
задачка3. Обоснуйте, что на всякой карте найдётся страна, граничащая не наиболее чем с пятью странами.
Решение. Если число государств на карте не превосходит 6, то утверждение задачки разумеется. Мы докажем, что на карте, имеющей наиболее 6 государств, найдутся даже четыре страны, любая из которых граничит не наиболее чем с пятью странами. Окрасим верхушки и дуги начальной карты в чёрный цвет, а красноватой краской отметим в каждой стране по одной точке. Всякие две отмеченные точки, лежащие в примыкающих странах (другими словами странах, имеющих общую граничную дугу), соединим снутри этих государств красноватой дугой так, чтоб красноватые дуги попарно не пересекались. Тогда всякие две красноватые точки будут соединены цепочкой дуг, и потому что никакие две построенные дуги не будут соединять одни и те же точки, то любая страна на карте, состоящей из точек и дуг красноватого цвета, будет ограничена не наименее чем 3-мя дугами. Если какая-то страна на данной нам карте ограничена наиболее чем 3-мя дугами, то на её границе можно избрать две верхушки, не соединённые дугой, и соединить их красноватой дугой снутри данной нам страны. Повторяя пару раз эту операцию, мы получим красноватую карту, на которой любая страна ограничена ровно 3-мя дугами. Потому что, не считая того, на данной нам карте никакие две дуги не соединяют одни и те же верхушки и потому что число вершин больше трёх, то из каждой верхушки выходят не наименее чем три дуги. Обозначим через n число дуг, через l — число государств, через m — число всех вершин красноватой карты и через a — число вершин, из которых выходят наименее чем 6 дуг. Тогда получим
3l = 2n,
(1)
3a + 6(m – a) ≤ 2n.
(2)
Из формулы (1) и аксиомы Эйлера, применённой к системе точек и дуг красноватого цвета, следует, что
2n = 6m – 12,
3a + 6(m – a) ≤ 6m – 12.
которое указывает, что a≥4. Остаётся увидеть, что если некая страна на чёрной карте имеет больше 5 соседей, то из отмеченной в данной нам стране красноватой точки выходит больше 5 дуг, и поэтому, в силу неравенства a≥4, на чёрной карте найдутся четыре страны, любая из которых имеет не больше 5 соседей.
Задача4. Можно ли семиугольник разрезать на выпуклые шестиугольники?
Решение. Представим, что некий семиугольник удалось разрезать на выпуклые шестиугольники. Обозначим число тех вершин шестиугольников, которые лежат снутри начального семиугольника, через m, а число оставшихся вершин (другими словами лежащих на границе семиугольника) — через m’. В качестве дуг, соединяющих верхушки, выберем прямолинейные отрезки сторон многоугольников, удовлетворяющие последующему условию: отрезок должен соединять две верхушки и не проходить через другие верхушки. Обозначим через n число таковых дуг и через l — число областей, на которые эти дуги делят плоскость (число l на единицу больше числа шестиугольников). Ясно, что любые две верхушки окажутся соединёнными цепочкой дуг. В силу аксиомы Эйлера
m + m’ – n + l = 2.
(3)
Потому что наружная область ограничена m’ дугами, а любая из других — не наименее чем шестью дугами, то
2n ≥ 6(l – 1) + m’.
(4)
Из неких вершин на границе семиугольника выходят лишь две дуги. Обозначим число таковых вершин через a. Из всякой иной верхушки выходят по последней мере три дуги, так что
3m + 3(m’ – a) + 2a ≤ 2n.
Отсюда в силу равенства(3)
n ≤ 3l + a – 6.
Сравнивая это неравенство и неравенство(4), мы получаем
2a – m’ ≥ 6.
(5)
Потому что на границе семиугольника найдутся по последней мере две верхушки, из которых выходят дуги, ведущие вовнутрь семиугольника, то m’ – a ≥ 2. Из этого неравенства и неравенства (5) следует, что a ≥ 8.
С иной стороны, потому что семиугольник разрезан на выпуклые многоугольники, то всякая верхушка, из которой выходят две дуги, является верхушкой семиугольника, и поэтому a ≤ 7. Таковым образом, семиугольник недозволено разрезать на выпуклые шестиугольники.
]]>

 (4 оценок, среднее: 4,75 из 5)
(4 оценок, среднее: 4,75 из 5)